谈“问题教学”在初中数学教学中的实施
2014-12-23郑森财
郑森财

什么是问题教学?列尔耐尔说:“问题教学的本质在于学生由教师经常引入寻求有根据地解决对他们来说是新问题的办法的过程,由此他们就学会独立地获取知识、运用原先学过的东西和掌握从事创造性活动的经验。”《教育大辞典》中就“问题教学法”的阐述是:“通过设置情境,提出、解决问题进行教学。”一般认同观点:所谓问题教学,是指以问题为中心的教学,它是把教学内容化作问题,引导学生通过解决问题而掌握知识、形成能力、养成心理品质的过程。
随着新课程改革的不断深入,社会对学生的创新能力的要求也越来越高。这就要求课堂教学中开展行之有效的创新教育,培养学生的创新能力。近年来,国外提出了“问题解决作为学校教育中心”的观点。我们的教育教学实践也证实了这一点:任何创新都源于问题。笔者认为,让学生带着问题学习,带着问题进课堂,强化问题意识,是实施创新教育的重要手段,是培养学生创新能力的一条有效途径。下面我就问题教学在课堂教学各个环节的实施策略结合教学实例进行阐述。
一、设置问题,提高兴趣,引入新知。
1.根据前课知识,设计若干问题,引导学生回忆旧知识,温故而知新,并在题目中渗透本课新授内容,顺其自然地引入,降低学生学习难度。例如:在教学“直角三角形全等判定”时,我校文体馆文艺演出时的舞台背景正是两个全等直角三角形,我便以此创设问题情境:工人师傅是如何通过测量判定两个三角形是全等的?引导学生复习已学过的三角形的判定方法,再以工人师傅有更简便特殊的判定方法为切入口,激发学生学习欲望,引入本课。
2.联系当前生活实际结合教学内容创设问题情境,让学生深入其境,发现问题,思考问题,引出新课题,调动学生学习积极性。例如:教学“平行四边形判定”时,以我校创办“省级达标示范校”将建的示范楼地基为原型,提问:如何判断它是否是平行四边形?学生兴致高涨,个个争先恐后地举手发言,自然引出本课教学内容。
3.通过问题,设置认知障碍,激发学生求知欲,引入新课。例如:在教学“三角形角平分线性质”时,我以沿海大通道为具体情景,提出:如何在三条两两相交的公路内部建一个货物中转站,使它到三条公路的距离相等?而要解决这个问题正需运用角平分线的性质。在学生产生疑问时,适时引入新课,激起学生的求知欲。
二、设置问题,引导探索,发现新知。
在人的心灵深处,都有一种根深蒂固的需要,就是希望自己是一个发现者、探索者。我们在教学活动中,要让学生真正成为学习活动的主体,就应积极为他们提供自主探究的机会,适时调整学习活动,把静态的数学知识转化为动态的探索对象,做到学生能够探索的,教师不要代替;学生能够发现的,教师不去暗示。尽量给学生多一些思考的时间,多一些自主活动空间,多一些表现自己的机会,多一些探索成功的喜悦。要“蹲下身子”开启学生求知的天窗,善于借助学生已有的生活经验,在知识的连接点上巧设疑点,使学生的思维在“旧知固定点—新旧知识衔接点—新知增长点”链条上有序展开,促进学生良好认知结构的形成。在教学中可围绕以下方面设置问题引导探索。
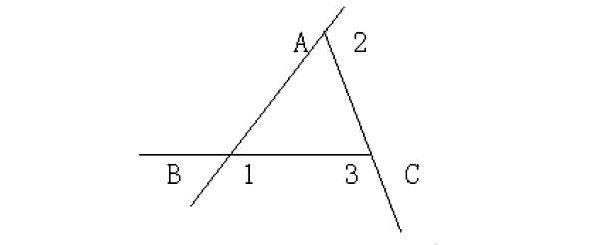
1.抓住新知识的增长点设置问题。学生是学习活动中的主体,要善于培养和调动学生的主体性,利用迁移规律,使学生掌握新知识的增长点,引导学生思考、探索,体会知识的生成过程,掌握新知。例如:在教学“三角形外角和”时,由于它是“三角形内角和”的推论,因此我结合“等式的基本性质”及“邻补角性质”设置问题如下:
如图在△ABC中,∠1+?摇?摇 ?摇?摇=180°
∠2+?摇 ?摇?摇?摇=180°
∠3+?摇 ?摇?摇?摇=180°
三式相加可以得到:∠1+∠2+∠3+∠?摇?摇?摇?摇+?摇?摇?摇?摇+∠?摇?摇?摇?摇=?摇?摇?摇?摇①
而∠ACB+∠BAC+∠ABC=?摇?摇?摇?摇②
将①与②相比较,你能得出什么结论?
学生在这些旧知识的增长点上,通过思考、探索、回答,在解决问题的过程中归纳总结出新知,感受到获得新知的愉悦感和成就感。
2.抓住新知识的学习方法设置问题。“未来的文盲不再是不识字的人,而是没有学会怎样学习的人”。这充分说明了学习方法的重要性,它是获取知识的金钥匙。学生一旦掌握了学习方法,就能自己打开知识宝库的大门。因此,在课堂教学中应根据学生学习特点,从数学思想、学习方法等方面入手,教给学生学习的方法和手段,提高学生的学习能力。例如:教学应用数形结合方法解题时,因“数形结合”思想是初中数学的重要思想,也是学习的一个难点,教学时可以从“数”—“形”或“形”—“数”设置问题,引导学生抓住两者之间的联系。如:在教学“求直线与坐标轴围成三角形面积”时,我设计问题如下:
①三角形的面积公式是什么?
②直线与坐标轴围成一个什么三角形?该三角形的底和高分别是哪些线段?
③欲求这些线段需先求哪些点的坐标?
④上述点的坐标有何特点?如何求得?
将分析过程转化成问题形式,学生在解决一个个小问题时,一层一层地将几何问题转化成代数问题,渗透“数形结合”思想方法,并引导学生分析、解决问题,形成能力。
3.根据重难点设置问题。重点往往是新知识的起点和主体部分,难点是大多数学生不易理解和掌握的知识点,难点和重点有时一致,根据教材的广度、深度和学生基础确定。围绕重难点设置问题,让学生在解决问题中加深对知识点的记忆和理解。例如:“反比例函数图像和性质”既是重点又是难点,教学时为让学生更易掌握,设置问题如下:画出函数y=6/x的图像,回答下列问题。
①这个函数图像在哪两个象限?和函数y=-6/x有什么不同?由此可知反比例函數图像在什么象限?由什么确定?
②在第一象限:x增大,y将如何变化?在第三象限呢?有什么规律?
③分别讨论当k>0时,k<0时,y随x变化的情况?
通过这些问题让学生层层深入,从易到难,突破难点。
4.化整为零,设置问题,各个击破。应用题对许多学生来说是个难点,新课标下的应用题更是非常生活化,很多题目的阅读量大、牵涉面广,学生理解起来较难。因此,教学中若能将题目根据不同要素分解成若干小问题,采用各个击破,再有机结合,便可让学生更轻松地掌握。例如:教学“行程问题”时,其关键在三个要素——路程、速度、时间,教学时围绕这三个要素根据题意设计问题。比如:若设甲的速度为x千米/小时,则乙的速度为多少?由此可得甲、乙所用的时间为多少?题目中的等量关系体现在哪句话?因此列出方程为:?摇?摇 ?摇?摇。这些小问题引导学生抓住题目中的等量关系、数量关系,解决问题就轻而易举了。
总之,对新知识的教学方式、方法有多种多样,如果将新知识的学习通过转化成若干小问题,让学生运用所学知识与他人合作交流去解决,则不仅能提高学生的学习兴趣,更能提高学生的学习能力和创新精神。
三、设置问题,强化训练,应用新知。
数学知识都是人们在生产、生活实践中总结出来的,并服务于生活,在应用所学新知识时,我们定能找到其生活中的原型或解决问題的一般方法设置问题,让学生运用所学知识解决问题,强化训练应用新知识。
1.结合生产实践设置问题,应用新知,体验数学服务于生活。例如:在教学“方程的应用”时,可与生活中的利润、行程、购物、存款等相结合设置问题;教学“对称图形”时,可根据我们身边的实物图形设置问题;教学“概率与统计”时,可直接以班级同学为对象设置问题;教学“函数”时,可结合生产实践设置问题。这些问题都是从生活中来的,学生在运用新知识解决问题时也能进一步了解数学的实用性,提高学习兴趣。
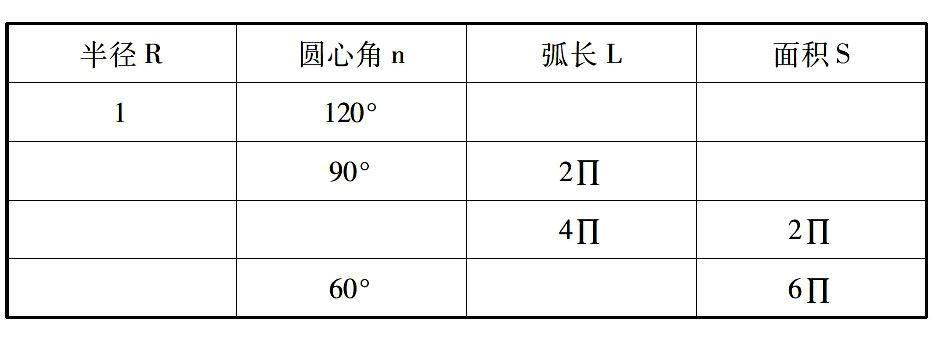
2.把握重点、难点设置问题,反复应用。新课标不提倡题海战术,在对新知识的记忆与应用注重学生在理解的基础上掌握,但若该知识点是初中数学的重点或是难点,为使学生熟练掌握,也可反复练习以达到熟能生巧。例如:教学“扇形弧长与面积公式”的应用时,设计表格如下:
学生根据同一个公式,在不同的已知条件下运用公式的变形完成表格,在解题中记忆公式并熟练掌握它的应用。
四、设置问题,课堂小结,回顾新知。
课堂小结是一堂课的有机组成部分。它不仅有利于学生加深对所学知识的理解和掌握,使知识条理化、系统化;而且有利于培养学生的概括能力,帮助学生掌握数学思想和方法;激发学生自主探索的求知欲望,激发学生学习兴趣。巧妙的课堂小结对整堂课能起到“画龙点睛”的作用。明代文学家谢榛说得好:“起句当如爆竹,骤响易彻;结句如撞钟,清音如余。”的确,一堂课如一首乐曲,结尾犹如曲终时留下袅袅不尽的余音。因而,在课堂教学中,我们必须精心设计好结语,使学生产生余兴未消,意犹未尽之感。
在新知识学完,教师利用一节课结束前的几分钟,提出问题作为结束语,简明扼要地对本节内容进行归纳小结。一方面可以让学生回忆所学知识的内容,并帮助学生加以梳理,辨清知识之间的联系和区别,加深对知识的理解。另一方面进一步强调教学重点和难点,促进学生认知结构的建立和完善,从而提高学生运用知识解决问题的能力。如:教学“角”时,师生共同小结,教师提出:①这节课我们学了什么内容?②角有几种表示方法?③什么样的角叫平角?什么样的角叫周角?④角有哪些度量单位?它们是什么关系?最后,让学生联系生活实际说出学习本课知识可以帮我们解决生活中的什么问题。这样,既巩固了所学知识,提高了学生的口头表达能力,“活学活用”,又增强了学生解决生活实际问题的能力,真正体现了新课标“生活数学”的理念。
“问题教学”的实施方法有很多,我在此抛砖引玉,以得到同仁的指教,其目的在于让一堂课的各个环节都能体现“问题教学”的闪光之处,进一步深化数学课堂教学改革。
