任意梯度分布功能梯度板的二维热弹性振动分析
2014-12-23刘五祥
刘五祥
(同济大学航空航天与力学学院,上海200092)
因此,只要求得Nm(0),就可以确定Nm(z).
由热力学边界条件式(7),(8)可得
功能梯度材料是一种不同于均匀材料和传统复合材料的新型非均匀材料,其概念是在20世纪80年代后期,由 Y.Tanigawa[1]在研究、设计高温热阻材料时提出,这种材料一般由2种物理性质完全不同的材料(比如陶瓷和金属)复合而成,从宏观上看,各个组份材料的体积分数在空间位置上是连续变化的,因而大大地缓解了由于材料参数的突变而导致的应力集中现象.
国内外对功能梯度材料梁、板、壳热问题的研究逐渐形成热点,但大多数学者都是采用比较特定的材料分布形式(如指数分布、线性分布等)来进行研究.如基于剪切理论,Yang Jie等[2]考虑材料物性参数随坐标和温度变化,研究了热、机械载荷作用下功能梯度材料矩形厚板的弯曲行为、动力特性以及瞬态响应;王颖泽等[3]基于线性热弹性理论,将修正的非傅立叶导热方程与热弹性运动方程联立,构建了急速热冲击作用下计及运动加速效应和非傅立叶效应的热弹性动力学模型;A.Sutradhar等[4]假设材料的物性参数在一个方向按指数变化,利用Green函数研究了三维功能梯度材料的瞬态热传导问题;J.Q.Tarn 等[5]假设材料参数沿径向幂函数变化,利用状态空间法对各向异性功能梯度材料柱形圆管的热传导问题进行了分析,他们利用特征函数展开和矩阵代数学获得了在一般热边界条件下,功能梯度材料管的瞬态和稳态热传导的解析解;B.V.Sankar等[6]从弹性力学方程出发,假定弹性模量沿厚度指数分布,得到了平面应变热响应问题的精确解;M.Ohmichi等[7]假设材料的热传导率是位置坐标的指数分布,对具有倾斜边界的功能梯度材料板,利用分离变量法获得了在其局部作用热荷载时的解析解.然而对于任意梯度分布的情况,还没有有效的方法来求解.
基于此,笔者提出一种新的求解方法,获得功能梯度平板热弹性弯曲问题的Peano-Baker级数解.通过算例,验证Peano-Baker级数解的正确性,同时也分析材料参数沿板厚方向为线性分布时,不同的激励频率对平板响应的影响.
1 问题的描述与基本方程
板的平面弯曲如图1所示,考虑一沿y轴方向无限长的正交各向异性功能梯度热弹性板(宽度为a,厚度为h),其对边简支、温度恒定,在板受柱型弯曲作用时,所有物理量与坐标y无关.
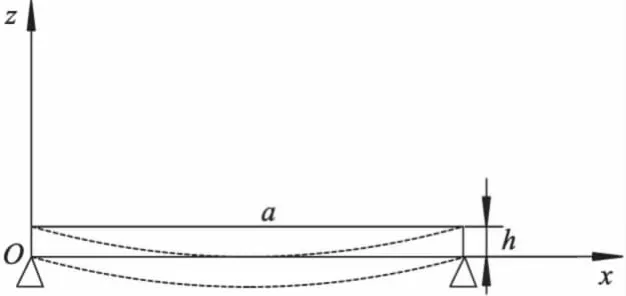
图1 板的平面弯曲
无体力情况下,运动方程为

热学平衡方程为
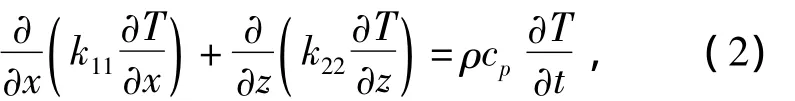
对于正交各向异性材料,本构方程为
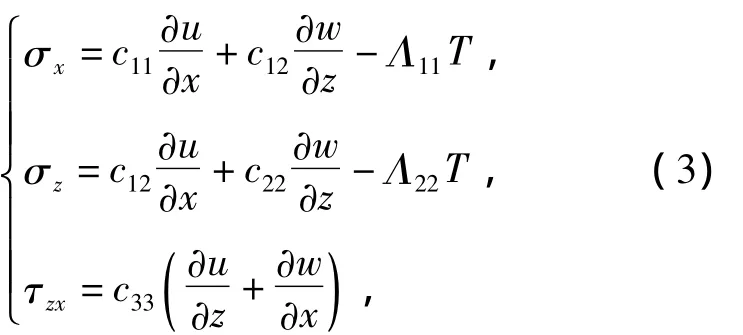
式中:u,w为位移;σx,σz,τzx为应力;T为温度;c11,c12,c22,c33为弹性常数;Λ11,Λ22为热模量;k11,k22为热传导系数;ρ为材料密度;cp为比热容.
假设上述所有材料参数均沿厚度方向按任意函数规律变化,即

式中:K为各种材料的常数;K0为相应材料常数在z=0处的值;F(z)为关于坐标z的任意函数,并且有F(0)=1.
x=0和x=a处的简支边界条件为

对于自由振动来说,上下表面的边界条件为
当z=0,h时,有

对于强迫振动来说,法向和切向应力以及温度可以展开成如下的形式,同时考虑满足上下表面时间协调形式的边界条件,即
z=0处(下表面),有
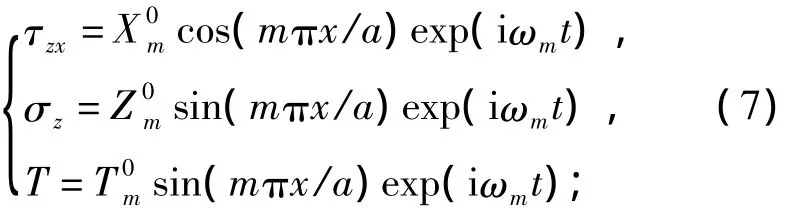
z=h处(上表面),有
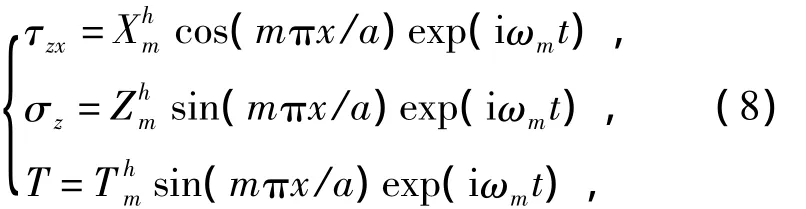
式中:m为正整数;ωm为圆频率.
热传导方程(2)是独立的,可由热学边界条件单独求出温度T,再联立式(1),(3),在力学边界条件下,即可确定板中的力场.
2 热传导方程的求解
假设热传导系数k11,k22满足式(4)的梯度变化规律,则热传导方程(2)可改写为
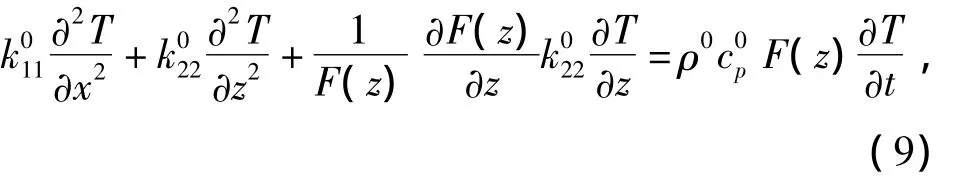
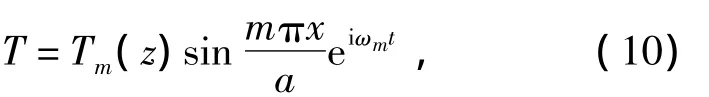
则自动满足x=0,a的热力学边界条件T=0.
将式(10)代入式(9)可得

假设T具有如下形式:
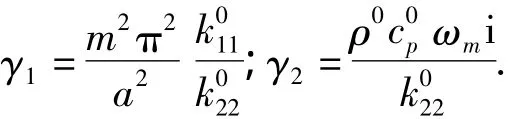
由变系数的线性微分方程组的矩阵形式解可知,可以把方程(11)化为如下的状态方程来求解:

其中:
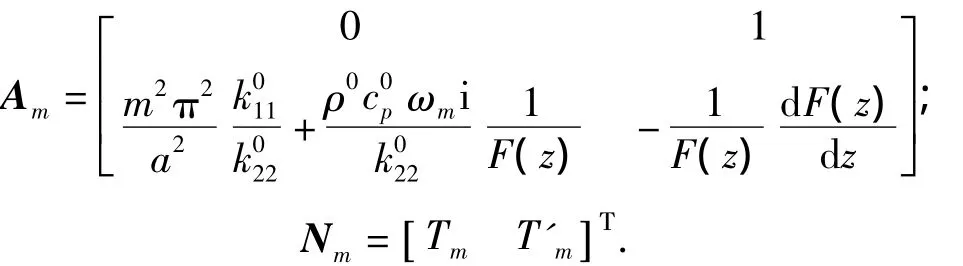
Am是坐标z的函数,状态方程(12)是1阶线性变系数的齐次微分方程组,它的通解为
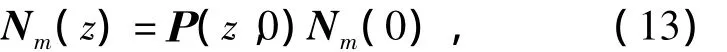
式中Ρ(z,0)为齐次变系数状态方程(12)的转移矩阵,可以化为关于矩阵Am的Peano-Baker级数形式[8]:
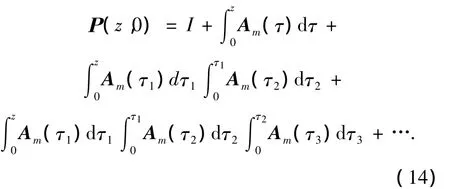
由式(13)可得

因此,只要求得Nm(0),就可以确定Nm(z).
由热力学边界条件式(7),(8)可得

将式(16)代入式(15)即可以确定T'm(0)和T'm(h).至此,就求得Nm(0).方程(12)的通解就完全确定了.方程(11)的解是式(12)解的第1个分量,方程(11)的解为
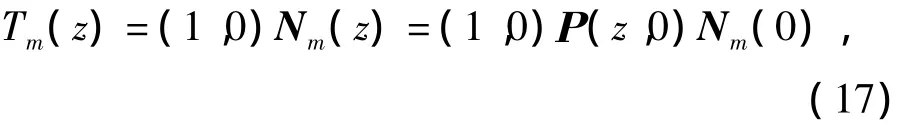
将式(17)代入式(10),这样温度场就可完全确定.
3 状态方程及其求解
由方程(1)和(3),消去σx可得

假设各状态量具有如下形式:
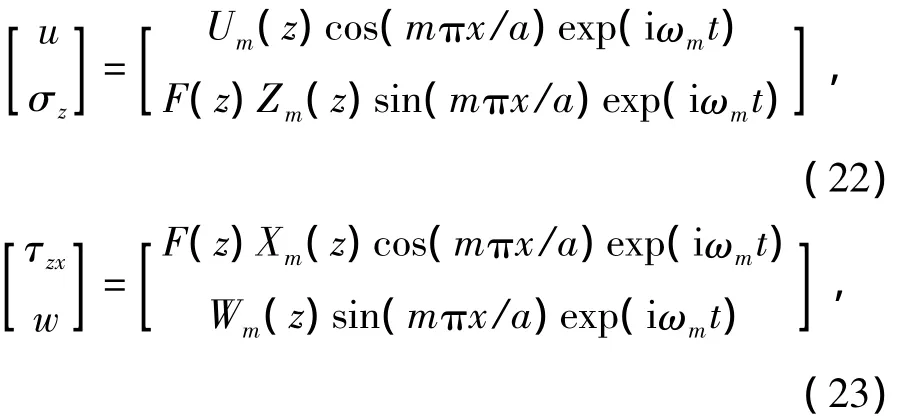
式(22),(23)自动满足对边简支的边界条件(5).
3.1 自由振动
将(22),(23)和(10)代入状态方程(18)可得
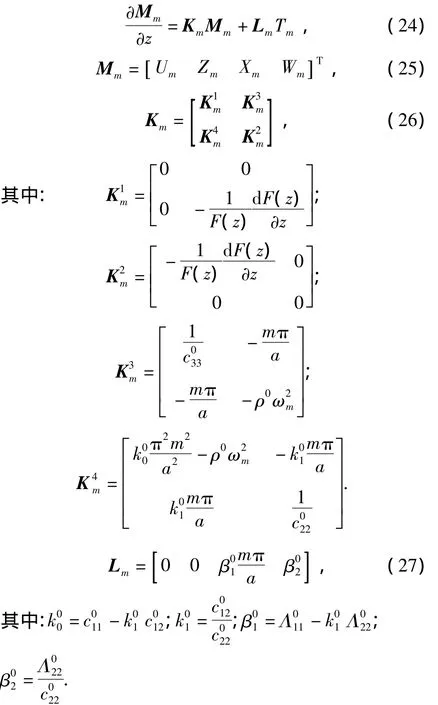
可以看出Km是坐标z的函数.状态方程(24)是1阶线性变系数的非齐次微分方程组,它的通解形式为

式中Φ(z,τ)为相应的齐次变系数状态方程的转移矩阵.
Φ(z,τ)可化为关于矩阵Km的 Peano-Baker级数形式[8]:
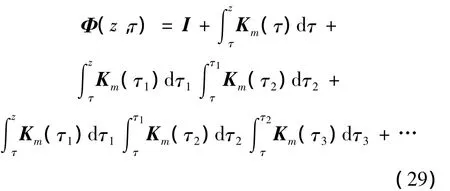
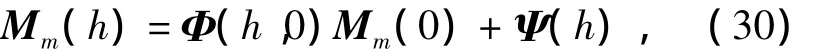
式(30)可以写成:
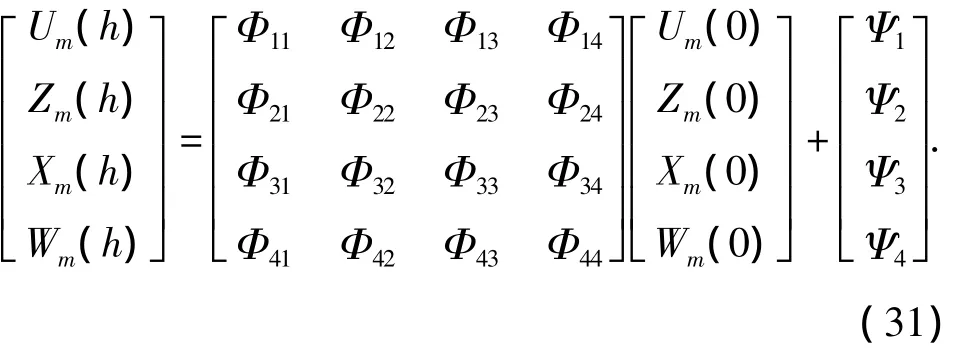
由于是自由振动,由式(6)可知:
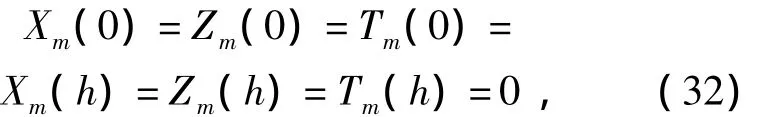
将式(32)代入式(31)可得
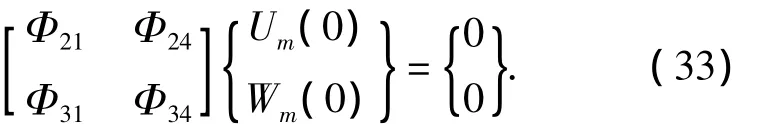
要使方程(33)有任意解,必需有
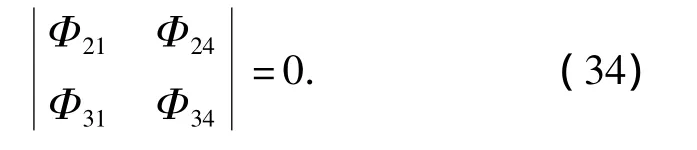
3.2 强迫振动
由边界条件(7)和(8)可得
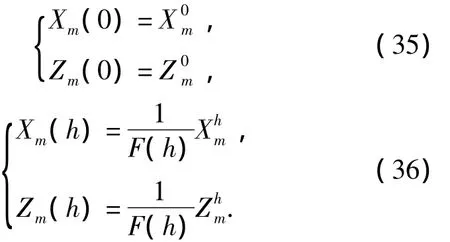
将式(34)中求得的固有频率ωm以及式(35)和(36)代入式(31)就可以确定Um(0),Wm(0),Wm(h)和Um(h).至此,求得了Mm(0).于是,状态方程(24)的通解Mm(z)就完全确定了,从而就可以求出热弹性功能梯度柱型弯曲板内任意点的解.其中,当ωm=0时,就是静载作用的解.
4 算例与分析
算例1 考虑一沿y轴方向无限长的功能梯度热弹性柱形弯曲板(a=1 m,h/a=0.1),对边简支、温度恒定.在z=0处的材料常数取为文献[9]所列的相应数据,如表1所示,N为式(14)和(29)所取项数.材料参数
表1 文中解和精确解最小固有频率的比较 10-2

表1 文中解和精确解最小固有频率的比较 10-2
的解0.1 0.374 66 0.326 01 0.373 14 0.374 63 0.374 66 0.h/a 精确解 N=6的解 N=8的解 N=10的解 N=12的解 N=14 374 66 0.2 1.409 23 1.032 68 1.391 80 1.408 69 1.409 22 1.409 23 0.3 2.910 95 4.599 17 2.797 51 2.905 30 2.910 76 2.910 95 0.4 4.699 36 14.032 10 4.161 90 4.662 10 4.697 43 4.699 27 0.5 6.650 20 17.540 10 4.141 12 6.470 00 6.637 46 6.649 53
4.1 自由振动
根据文献[10]的方法可以求得精确解.为了验证Peano-Baker级数求解的正确性,现假设所有的材料弹性常数沿板厚方向指数分布,即

式中:α为材料的梯度变化参数,取α=1;h为板厚.
从表1可以看出:随着式(14)和(29)中Peano-Baker级数所取项数N的增加,其解也越来越接近精确解.当N=10时,其与精确解的相对误差已小于5%.因此,在利用Peano-Baker级数求解的过程中,只要取较少的几项就可以满足一般计算精度的要求;随着功能梯度热弹性板厚宽比的增大,此级数解的收敛速度相对变慢.在后面的计算中均取N=10.
4.2 强迫振动
算例2 考虑一沿y轴方向无限长的功能梯度热弹性柱形弯曲板(a=1 m,h/a=0.1),对边简支、温度恒定.设热弹性板下表面的材料参数见算例1,所有的材料弹性常数沿板厚方向是线性分布的,即
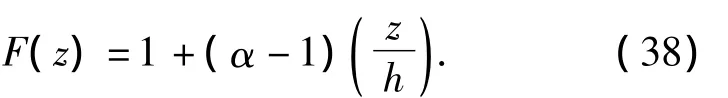
当材料的梯度变化参数α=2、厚宽比h/a=0.1时,板内x/a=1/4处,在静载荷(ω=0)和强迫振动频率(ω =0.85ω0,ω =0.95ω0,ω =1.05ω0)时,各场量沿z轴的分布,如图2,3所示,ω0为固有频率ω1的最小值.
工况1为机械荷载作用,上表面(z=h)处有σz= -Z0sin(πx/a)exp(iωt),取Z0=1 Pa,σzx=T=0;下表面(z=0)处有 σz=σzx=T=0.
工况2为热荷载作用,上表面(z=h)处有T=T0sin(πx/a)exp(iωt),取T0=1 K,σz= σzx=0;下表面(z=0)处有 σz=σzx=T=0.
从图2,3可以看出:水平位移u沿厚度方向呈现放射状变化,而垂直位移w不管是静载(ω=0),还是在动载(ω≠0),几乎都是均匀变化.由于弹性常数,热模量和热传导系数均为厚度坐标的函数,因此,离面应力σzx、面内应力σx不再是厚度坐标的线性函数;位移、应力均随着激励频率接近板的固有频率,其值也增大.
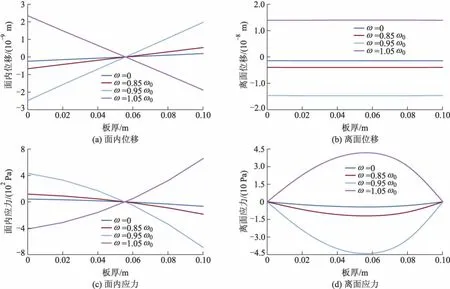
图2 机械荷载作用下各物理量沿厚度方向的变化
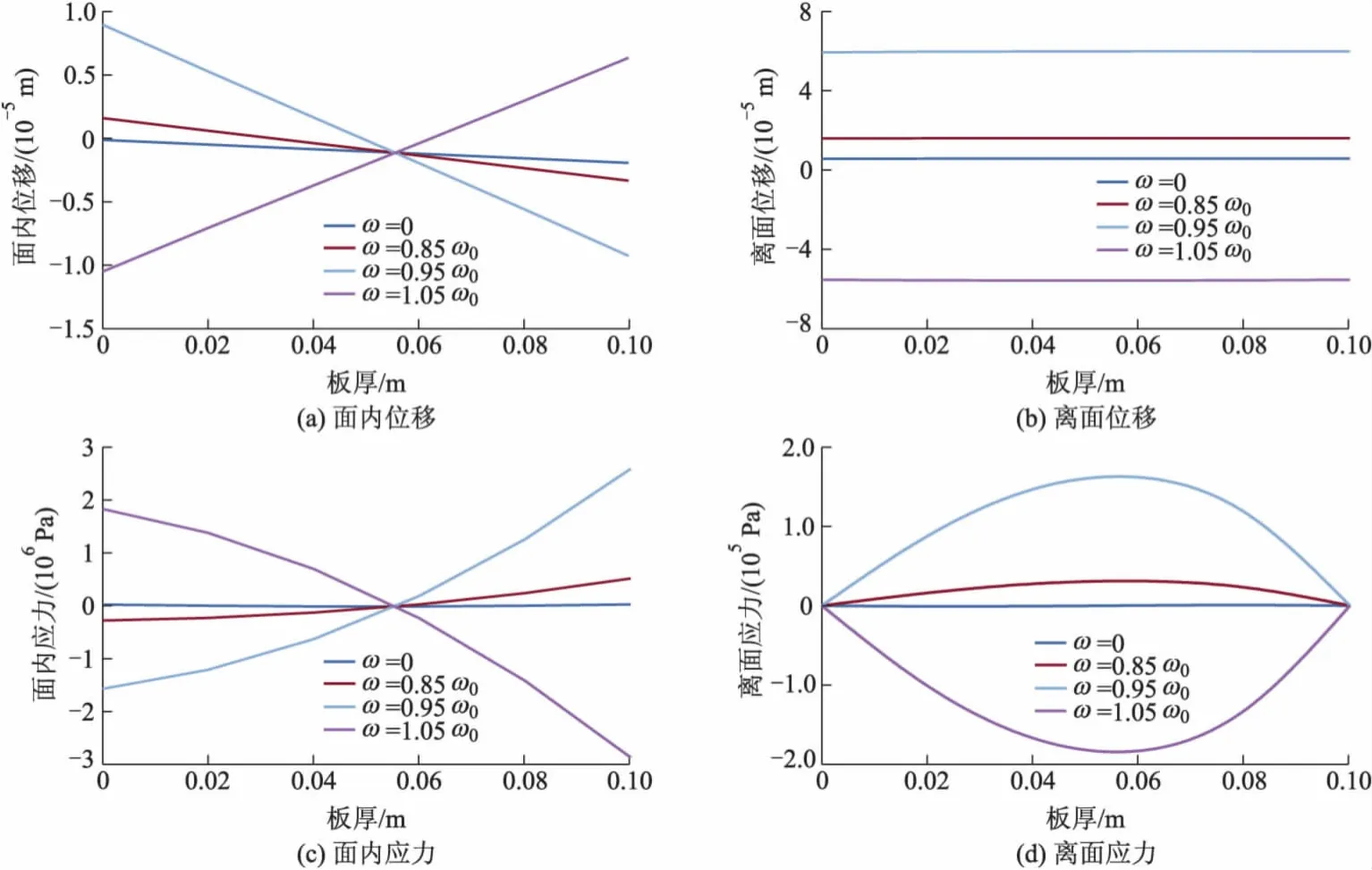
图3 热荷载作用下各物理量沿厚度方向的变化
5 结论
提出了二维正交各向异性功能梯度板热弹性振动问题的Peano-Baker级数求解方法.算例结果表明:Peano-Baker级数解具有收敛性好、理论推导简单、计算效率高等优点,且适用于材料弹性参数沿板厚方向任意函数梯度变化的情况,是一种进行功能梯度结构热振动分析的有效方法.
References)
[1]Tanigawa Y.Some basic thermoelastic problems for nonhomogeneous structural materials[J].Applied Mechanics Reviews,1995,48(6):287 -300.
[2]Yang Jie,Kitipornchai S,Liew K M.Large amplitude vibration of thermal-electro-mechanically stressed FGM laminated plates[J].Computer Methods in Applied Mechanics and Engineering,2003,192(35/36):3861-3885.
[3]王颖泽,张小兵,葛风华.急速热冲击作用下实心球体的热弹性响应分析[J].江苏大学学报:自然科学版,2012,33(4):414-419.Wang Yingze,Zhang Xiaobing,Ge Fenghua.Thermoelastic response of a solid sphere under transient thermal shock [J].Journal of Jiangsu University:Natural Science Edition,2012,33(4):414 -419.(in Chinese)
[4]Sutradhar A,Paulino G H,Gray L J.Transient heat conduction in homogeneous and non-homogeneous materials by the Laplace transform Galerkin boundary element method[J].Engineering Analysis with Boundary Elements,2002,26(2):119 -132.
[5]Tarn J Q,Wang Y M.Heat conduction in a cylindrically anisotropic tube of a functionally graded material[J].Chinese Journal of Mechanics Series A:English Edition,2003,19(3):365-372.
[6]Sankar B V,Tzeng J T.Thermal stresses in functionally graded beams[J].AIAA Journal,2002,40(6):1228 -1232.
[7]Ohmichi M,Noda N.Two-dimensional heat conduction problem in a functionally graded plate with a slanting boundary to the functional gradation[J].Journal of Thermal Stresses,2007,30(7):715 -730.
[8]Dacunha J J.Transition matrix and generalized matrix exponential via the Peano-Baker series[J].Journal of Difference Equations and Applications,2005,11(15):1245-1264.
[9]刘五祥,仲 政.功能梯度平板的二维热弹性分析[J].力学季刊,2008,29(1):40-47.Liu Wuxiang, Zhong Zheng. Two-dimensional thermoelastic analysis of a functionally graded plate[J].Chinese Quarterly of Mechanics,2008,29(1):40 -47.(in Chinese)
[10]Zhong Zheng,Yu Tao.Vibration of a simple supported functionally graded piezoelectric rectangular plate[J].Smart Materials and Structures,2006,15:1404 -1412.
