严格对角占优M-矩阵A的‖A－1‖∞上界的新估计式

杨晓英，曾宝国，朱清溢，刘 新

(1.四川信息职业技术学院a.基础教育部;b.电子工程系，中国广元 628017;2.电子科技大学物理电子学院，中国成都 610054)

M-矩阵是一类有着广泛应用背景的重要矩阵.生物学、物理学、经济学和社会科学中的许多问题都和M-矩阵有着密切的联系.在数值分析和求解初值问题的常微分线性方程组等问题中，经常需要判断实矩阵A ∈Rn×n的A－1在无穷大范数下的界，但是当A－1很难精确求出时，‖A－1‖∞通常是很难计算的.所以，当A 是严格对角占优的M-矩阵时，关于‖A－1‖∞的上界估计成为许多学者关注和研究的热点，已获得了一系列估计式［1-7］，本文将继续这一问题的研究，给出‖A－1‖∞上界的新估计式.

设N 表示自然数;Rm×n(Cm×n)表示m×n 阶实(复)矩阵的集合;ρ(P)表示n×n 阶非负矩阵P 的Perron根.将所有非对角元素都为非正实数的n 阶方阵的集合记为Zn.设矩阵A=(aij)∈Rn×n，若aij≥0，i，j ∈N，则称矩阵A 为非负矩阵，记A ≥0.

设矩阵A=(aij)∈Zn，则A 可以表示为A=λI－B，其中B ≥0，当λ ≥ρ(B)时，称A 为M-矩阵.特别地，当λ ＞ρ(B)时，称A 为非奇异M-矩阵;当λ=ρ(B)时，称A 为奇异M-矩阵.并记Mn表示n 阶M-矩阵的集合.

设A ∈Mn，记，其中σ(A)表示矩阵A 的谱.τ(A)称为矩阵A 的最小特征值.同时，有.

首先给出一些记号，它们将在后面的讨论中用到.记:

显然，ρi=vi+ui.

定义1［1］设矩阵A=(aij)∈Rn×n，且满足下列条件:

(3)对∀i ∈N，i ∉J(A)，存在非零元素序列aii1，ai1i2，…，airk，其中i ≠i1，i1≠i2，…，ir≠k，k ∈J(A)，则称A 为弱链对角占优矩阵.

定义2［11］设矩阵A=(aij)∈Rn×n，对于i，j ∈N，i ≠j，有aij≤0，aii＞0，则称A 为L-矩阵.

定义3［11］设矩阵A=(aij)∈Rn×n，若，i ∈N，则称矩阵A 为行严格对角占优矩阵.

定理1［1］设A=(aij)∈Rn×n是弱链对角占优M-矩阵，A－1=(αij)，τ=τ(A)，则

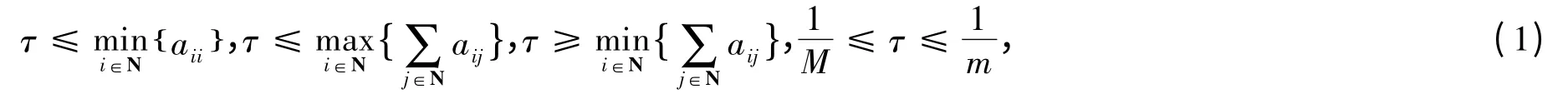
Varah 在文献［2］中给出严格对角占优M-矩阵的‖A－1‖∞上界估计:

Cheng 等在文献［3］中给出严格对角占优M-矩阵的‖A－1‖∞上界估计:

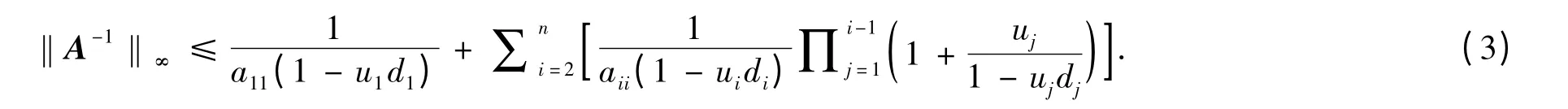
Wang［4］改进了Cheng 的结果，得到

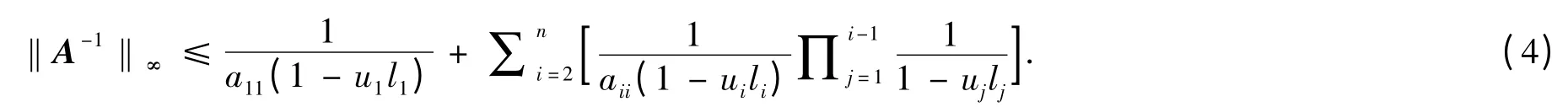
上述结论也可以用于估计严格对角占优M-矩阵的最小特征值的下界.

本文将继续这一问题的研究，给出严格对角占优M-矩阵逆矩阵的无穷大范数‖A－1‖∞上界的新估计式，理论证明和数值算例表明新估计式改进了一些已有结果.另外，利用(1)式得到严格对角占优M-矩阵最小特征值的一个新下界.

1 严格对角占优M 矩阵的无穷大范数‖A－1‖∞上界的估计

引理1［1］设A=(aij)∈Rn×n是弱链对角占优矩阵，A－1=(αij)，则

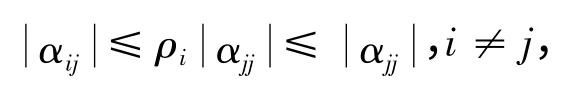
且对于i ∈J(A)，有

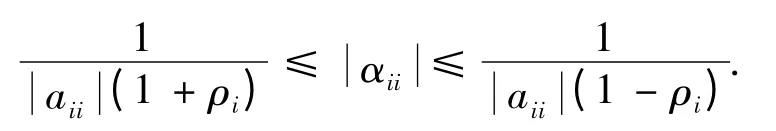
引理2设A=(aij)∈Rn×n是行严格对角占优M-矩阵，A－1=(αij)，则

当j=1 时

且

证(5)式的证明见文献［12］中引理2.2.下面证明(6)，(7)两式.

由si，vk和wk的定义知.由此(6)式的右半部分成立.由AA－1=I，可知.因此

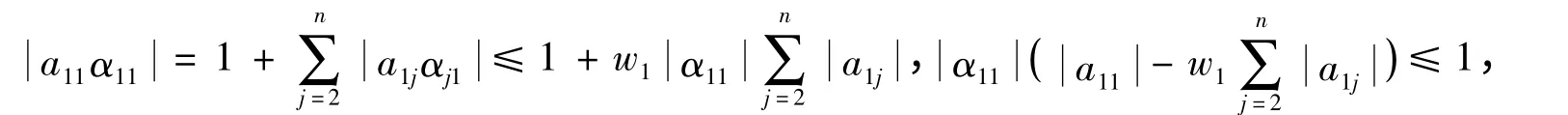
同理，(7)式的左半部分也成立.

设非空指标集合β(k)⊆N，定义A［β(k)］表示取自矩阵A 的行列式都是β(k)的子矩阵.定义A(k)=A［α(k)］，其中;例如A(1)表示删除A 的第一行第一列的子矩阵.

引理3［1］弱链对角占优L-矩阵是非奇异M-矩阵.

引理4［1］设A=(aij)是n 阶弱链对角占优M-矩阵，则B=A(1)是(n－1)×(n－1)阶弱链对角占优M-矩阵.(即B－1=(βij)存在，且βij≥0，i，j=2，3，…，n).

引理5［1］设A=(aij)∈Rn×n是弱链对角占优M-矩阵，B=A(1)，A－1=(αij)，B－1=(βij)，则

定理2设A=(aij)∈Rn×n是严格对角占优M-矩阵，B=A(1)，A－1=(αij)n×n，B－1=(βij)(n－1)×(n－1)，则

证令.则M1=max{ri，1 ≤，由引理2 及(8)式可得

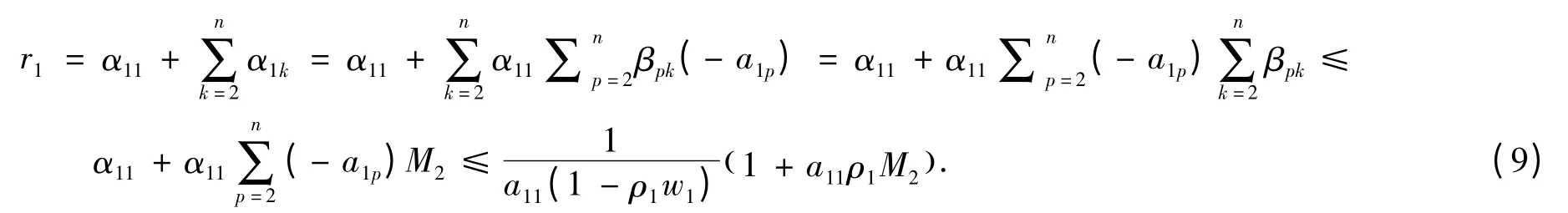
当2 ≤i ≤n 时，由(6)式及(8)式，得出

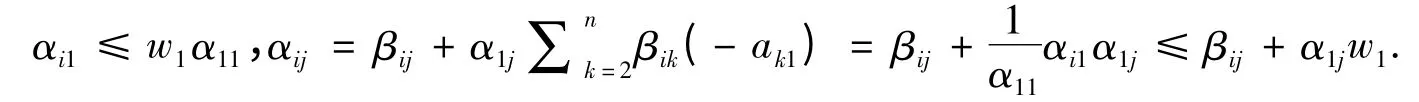
因此

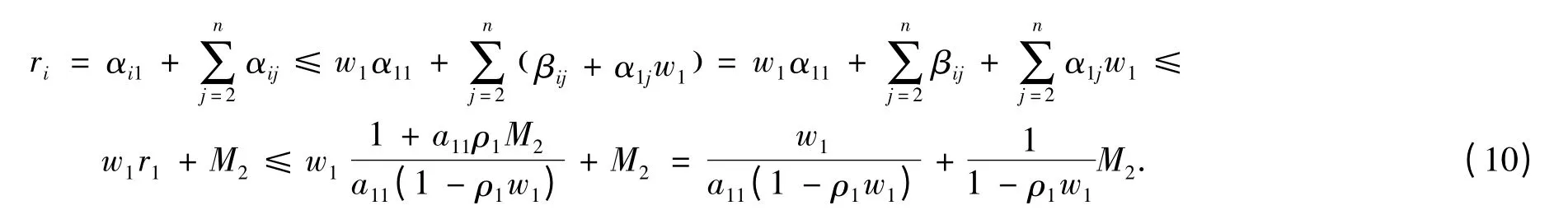
由(9)式与(10)式，可得

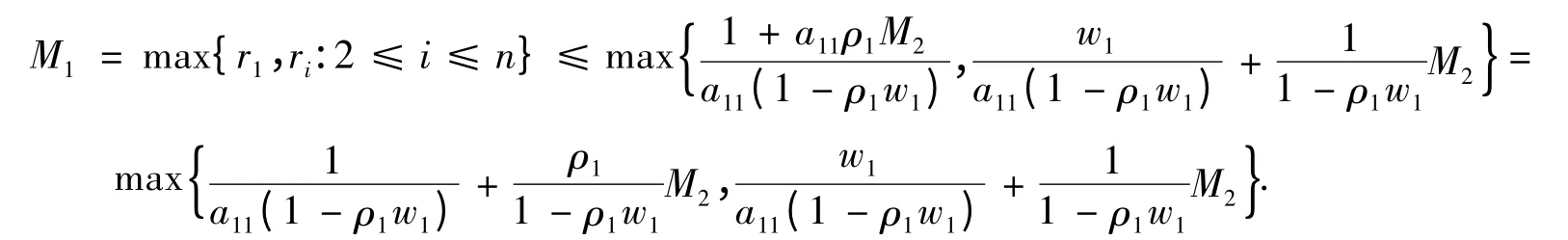
故结论成立.证毕.

定理3设A=(aij)∈Rn×n是严格对角占优M-矩阵，则

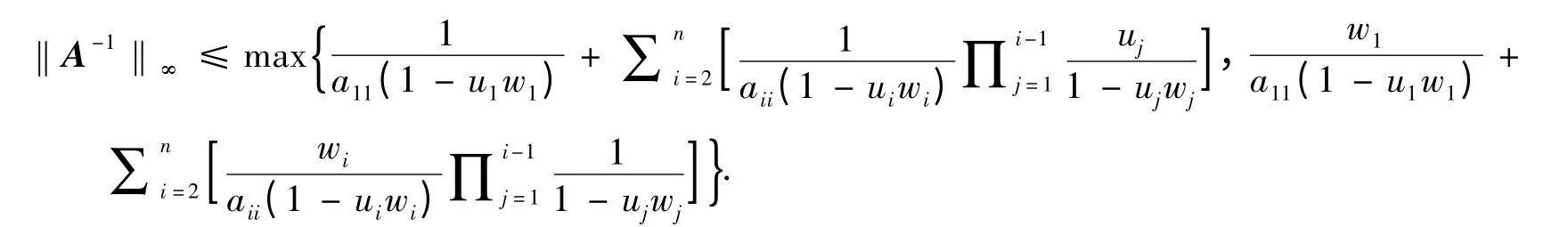
证由定理2 及A(k)的定义，可证明之.其中ρ1=u1，un=0，wn=1.

推论1设A=(aij)∈Rn×n是严格对角占优M-矩阵，则

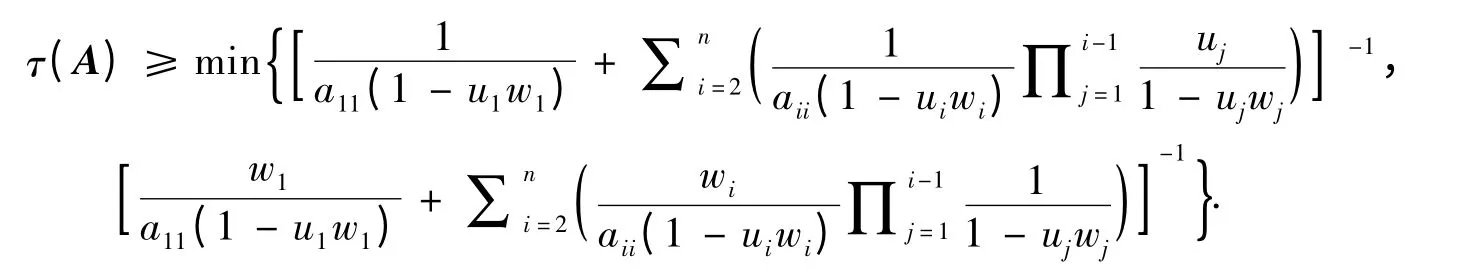
定理4设A=(aij)∈Rn×n是严格对角占优M-矩阵，则

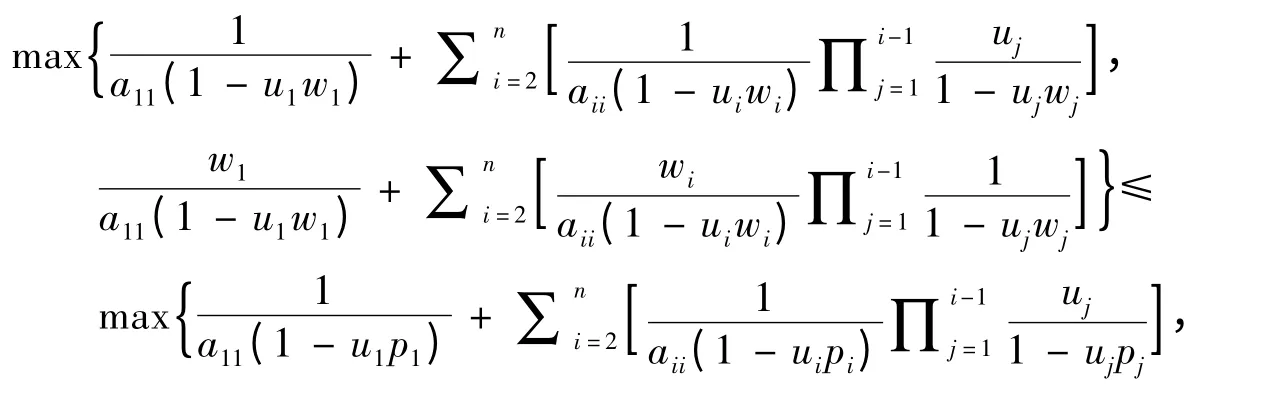
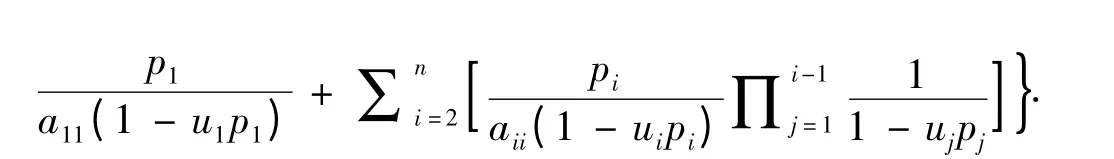
证由文献［12］中的定理3.3 的证明可知，si≤ρi，i=1，…，n，则由bk与vk的定义知v1≤b1.同理可证vk≤bk，k=2，…，n.所以wk≤pk，k=1，…，n.即故结论成立.证毕.

注由定理4 可知，定理3 在一定条件下改进了文献［5］中定理2 的结果.

2 算例分析

例1设

显然，矩阵A 是严格对角占优M-矩阵.易计算得‖A－1‖∞=2.33.则由(2)式得，‖A－1‖∞≤10;由(3)式得，‖A－1‖∞≤3.887 8;由文献［1］中定理3.3，‖A－1‖∞≤4.03;由(4)式得，‖A－1‖∞≤3.708 3;由文献［5］中定理2，‖A－1‖∞≤2.554 0;由本文的定理3，得‖A－1‖∞≤2.544 8.

注例1 表明，定理3 的结果改进了一些已有结果.

［1］SHIVAKUMAR P N，WILLIAMS J J，YE Q，et al.On two-sided bounds related to weakly diagonally dominant M-matrices with application to digital circuit dynamics［J］.SIAM J Matrix Anal Appl，1996，17(2):298-312.

［2］VARAH J M.A lower bound for the smallest singular value of a matrix［J］.Linear Algebra Appl，1975，11(1):3-5.

［3］CHENG G H，HUANG T Z.An upper bound for ‖A－1‖∞of strictly diagonally dominant M-matrices［J］.Linear Algebra Appl，2007，426(2/3):667-673.

［4］WANG P.An upper bound for ‖A－1‖∞of strictly diagonally dominant M-matrices［J］.Linear Algebra Appl，2009，431(5/7):511-517.

［5］HUANG T Z，ZHU Y.Estimation of ‖A－1‖∞for weakly chained diagonally dominant M-matrices［J］.Linear Algebra Appl，2010，43(2/3):670-677.

［6］VARGA R S.On diagonal dominance arguments for bounding ‖A－1‖∞［J］.Linear Algebra Appl，1976，17(3):211-217.

［7］LI W.The infinity norm bound for the inverse of nonsingular diagonal dominant matrices［J］.Appl Math Lett，2008，21(3):258-263.

［8］HORN R A，JOHNSON C R.Topics in matrix analysis［M］.New York:Cambridge University Press，1991:113-115.

［9］JOHNSON C R.A Hadamard product involving M-matrices［J］.Linear Multilinear Algebra，1977，4(4):261-264.

［10］FIEDLER M，JOHNSON C R，MARKHAM T L，et al.A trace inequality for M-matrices and the symmetrizability of a real matrix by a positive diagonal matrix［J］.Linear Algebra Appl，1985，71(11):81-94.

［11］BERMAN A，PLEMMONS R J.Nonnegative Matrices in the Mathematical Sciences［M］.3rd Ed.New York:Academic Press，1994.

［12］LI Y T，CHENG F B，WANG D F.New lower bounds on eigenvalue of the Hadamard product of an M-matrix and its inverse［J］.Linear Algebra Appl，2009，430(4):1423-1431.