砻谷机喂料器隔振系统的优化分析
2014-12-20贾乐乐王凤成阮竞兰
贾乐乐 王凤成 阮竞兰
(河南工业大学机电工程学院,郑州河南 450007)
砻谷机振动喂料性能评价因素主要包括喂料器的喂料特性和隔振效果。其中,隔振效果的好坏通常通过隔振系数的大小加以评定,对于二次隔振系统,常采用动载荷幅值比来评判,其主要影响因子有频率比和质量比。本研究拟对砻谷机振动喂料器在隔振方面进行参数匹配和优化,利用群体智能优化方法——粒子群算法,对该振动系统中的动载荷幅值比进行优化,为砻谷机喂料器隔振系统的设计提供参考。
1 砻谷机喂料器动载荷幅值比
1.1 动载荷幅值比数学模型
砻谷机喂料器结构简图如图1所示,主要由料槽、激振器、主振弹簧、底座和隔振弹簧组成,具有输送效率高、负载能力强和结构简单等特点。其振动系统模型可看作是二自由度系统的受迫振动,不计阻尼的情况下,该模型可简化为如图2所示的结构简图。
根据图2简化模型以及拉格朗日方程,写出振动系统的微分方程为:
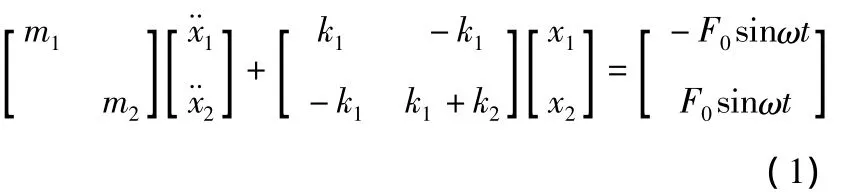
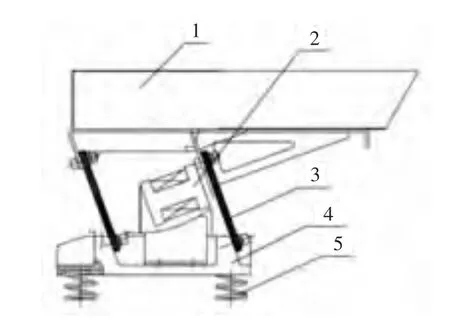
图1 砻谷机喂料器结构简图Figure 1 The structure diagram of Rubber Roller Husker Feeder
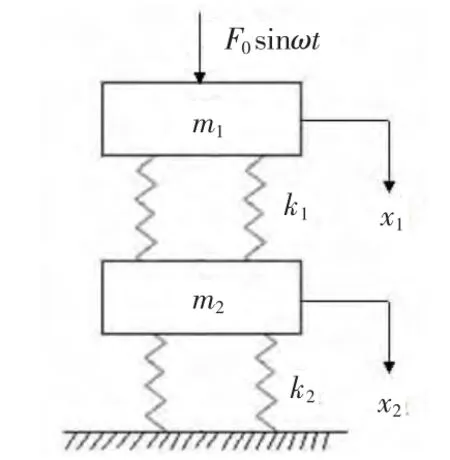
图2 二自由度系统的受迫振动模型Figure 2 The forced vibration model of two degree of freedom system
代入求解得:
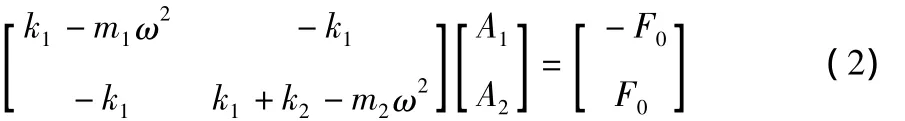
系统的固有频率与外界的激振力及其形式无关,假设喂料器所受的激振力为0,得:
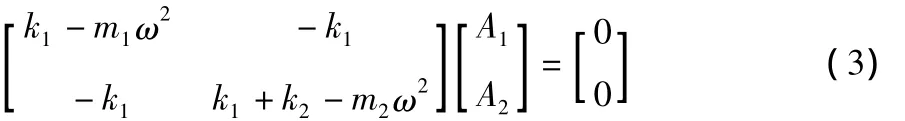
要使得方程有非零解,则:
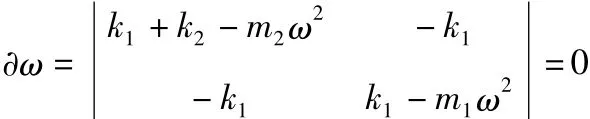
求解二自由度振动系统的两个固有频率ω01和ω02,简化后为:
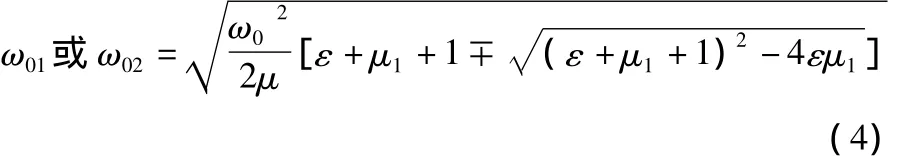
求得上质体振幅A1和下质体振幅A2的值分别为:
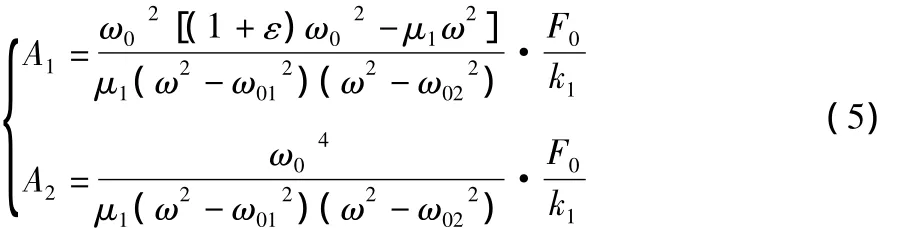
二次隔振传给地基的动载荷为:
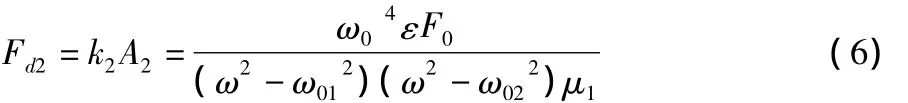
一次隔振传给地基的动载荷为:
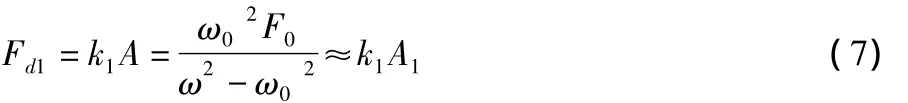
二次隔振与一次隔振传给地基的动载荷幅值之比为:
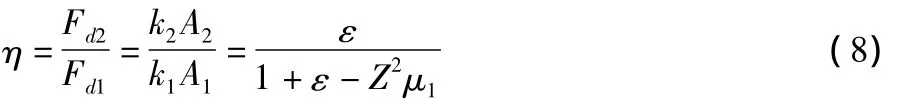
1.2 动载荷幅值比参数的数值模拟
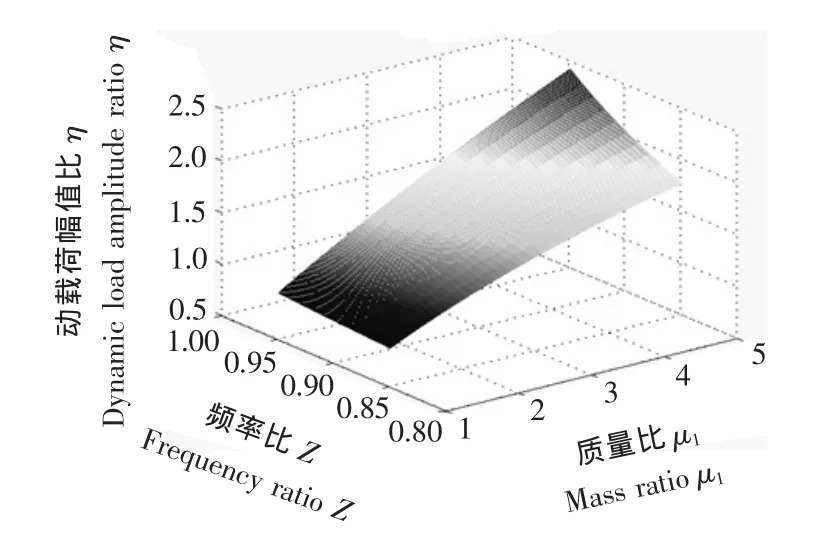
图3 η-μ1-Z三维网格图Figure 3 The 3D grid diagram of η - μ1- Z
2 粒子群算法
2.1 粒子群算法优化思想
粒子群算法(particle swarm optimization,PSO)能解决连续函数的最小值问题,是一种新兴的基于群体智能的启发式全局搜索算法,是群体智能优化方法之一。与其它优化算法相比,粒子群优化算法具有规则简单,容易实现;收敛速度快,可以避免陷入局部最优;可调参数比较少,搜索高效等优点[3],因此,在工程中应用比较广泛。
假设在一个D维的目标搜索空间中,有N个粒子组成一个群落,其中第i个粒子表示为一个D维的向量,记为:Xi=(xi1,xi2,…xiD),i=1,2,…N。
第i个粒子速度是一个D维的向量,记为:Vi=(vi1,vi2,…,vid,…,viD),i=1,2,…N。
第i个粒子搜索到的最优位置称为个体极值,记为:Pi=(pi1,pi2,…,pid,…,piD),i=1,2,…N。
整个粒子群搜索到的最优位置为全局极值,记为:
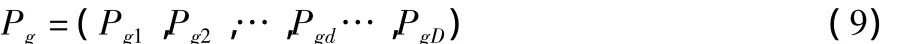
每次迭代的过程中,粒子根据式(10)和(11)来更新自己的速度和位置[4]:
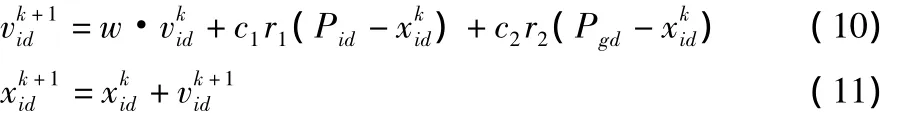
式中:
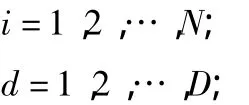
c1、c2——学习因子,也称加速常数;
k——迭代次数;
r1、r2——[0,1]范围内的均匀随机数。
2.2 粒子群算法的参数变量
合适的参数变量能有效提高粒子群算法的优化速度、精度和性能,设置的主要参数包括:种群规模N、最大迭代次数M、惯性权值w、加速因子c1,c2和粒子维数D等。
(1)种群规模N:种群太小不能提供足够的采样点,导致算法性能很差;种群太大尽管可以增加优化信息,但会增加计算量,造成收敛时间太长,表现为收敛速度缓慢。种群规模一般设为100~1 000。
(2)最大迭代次数M:迭代次数能保证解的收敛性,但是影响运算速度。
(3)惯性权值w:惯性权重w表示在多大程度上保留原来的速度。w较大,全局收敛能力强,局部收敛能力弱;w较小,局部收敛能力强,全局收敛能力弱,合适的惯性权重值可以平衡该算法的全局和局部寻优能力。通常情况下,w=0.1~0.9。
(4)加速因子c1、c2:加速常数c1和c2用于控制粒子指向自身或邻域最佳位置的运动。c1和c2值选择过大,粒子将会很快地越过目标区域;若选择过小,粒子将会飞离目标区域。合适的加速常数可以提高算法的速度且不陷入局部最优,通常取c1=c2=2。
(5)粒子维数D:粒子维数取决于待优化函数的维数。
3 优化过程及结果分析
根据粒子群优化算法的思想[5],针对原MLGQ36型胶辊砻谷机喂料器,以其动载荷幅值比为目标函数,编制相应的粒子群优化程序,主要包括主程序、更新粒子速度及位置的程序和求解程序3部分[6],其中的参数值设置见表 1[7],所得优化后的结果见图4[8]。

表1 粒子群优化算法中参数设置Table 1 Parameter Settings on PSO
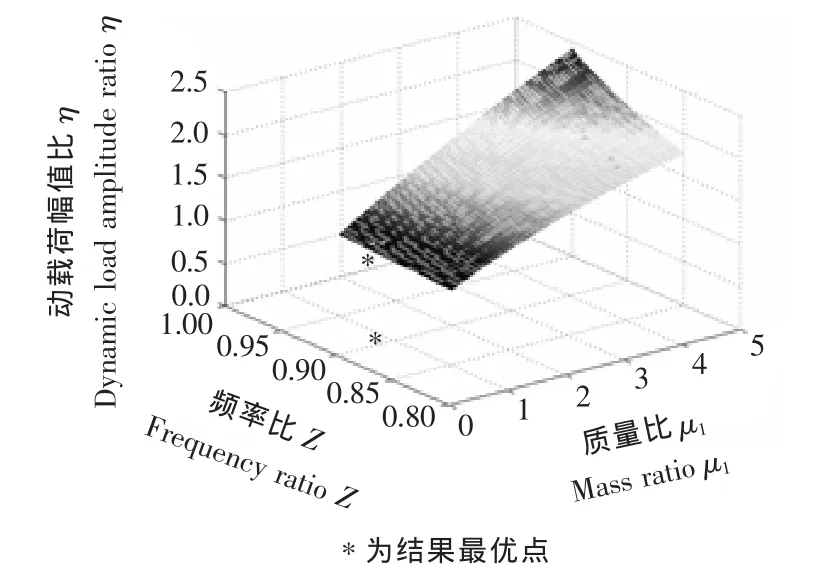
图4 粒子群优化结果Figure 4 The results after Particle Swarm Optimization
由粒子群优化结果可以看出,当频率比Z≈0.9,质量比μ1≈0.8时,动载荷幅值比取极小值 η≈0.836 4。优化前后结果对比如表2所示,优化后的动载荷幅值比要比优化之前小,说明优化后传给机架的动载荷较小,方案可行。

表2 优化前后结果对比Table 2 The pre and post optimization results compared
对于近共振振动机械,其主振频率比Z=ω/ω0≈1,通常选用的范围为Z=0.75~1.30。此时,若采用一次隔振时,隔振系数 η=k/mω2= ( ω/ω0)2=1/Z2;采用二次隔振可以有效降低传入机架的动载荷,减小整机的振动和噪音,对于振动喂料器来说,隔振系数必须小于许用值,需保证[η]<1.11~1.38[9]。优化后所得的结果小于许应值,满足实际工况所需的隔振效果。
4 结论
通过对砻谷机喂料器隔振系统进行建模和分析,得出二次隔振系统的动载荷幅值比关系式。针对原MLGQ36型砻谷机喂料器,利用MATLAB软件编制出相关的粒子群优化程序,以动载荷幅值比为目标函数,对其进行智能优化。结果表明,当振动系统中的频率比选择在Z=0.9附近,质量比选择在μ1=0.8附近时,动载荷幅值比取极小值η≈0.836 4。所得的结果较为优化,且满足实际工况的隔振效果,使得该喂料器传入机架的振动低、噪声小。
1 闻邦椿,刘树英.振动机械的理论与动态设计方法[M].北京:机械工业出版社,2001:93~94.
2 王正林,刘明.精通MATLAB[M].北京:电子工业出版社,2013:296~298.
3 纪霞.粒子群算法及应用[M].北京:科学出版社,2009:25~28.
4 高朝祥,王充.基于粒子群算法的曲柄滑块机构优化设计[J].食品与机械,2011,27(4):101 ~103.
5 雷秀娟.粒子群优化算法在函数优化中的应用及参数分析[J].计算机工程与应用,2008,44(28):53 ~55.
6 吴建生,秦发金.基于MATLAB的粒子群优化算法程序设计[J].柳州师专学报,2005,20(4):97 ~100.
7 Deyun.Hybrid particle swarm optimization and its application[J].Journal of Chemical Industry and Engineering,2008,59(7):1 707 ~1 710.
8 侯志荣,吕振肃.基于MATLAB的粒子群优化算法及其应用[J].计算机仿真,2003,20(10):68 ~70.
9 祝水琴.基于MATLAB软件的电磁振动喂料系统仿真[J].轻工机械,2009,27(2):65 ~67.
