基于多目标遗传算法的印制电子喷印机结构轻量化设计

顾春荣，刘德仿,，周临震，王 斌，廖 萍

GU Chun-rong1,LIU De-fang1,2,ZHOU Lin-zhen2,WANG Bin2,LIAO Ping1

（1.南通大学 机械工程学院，南通 226019；2.盐城工学院 机械工程学院，盐城 224051）

0 引言

随着科技的发展，印制电路板进入印制电子时代，其中印制电子喷印技术的应用尤为广泛[1]。印制电子喷印机利用其运动系统与喷头，在预先编制程序的控制下将导电性墨水喷到基材上从而形成线路，能像传统打印机那样大批量地印制电路板[2]。由于印制电子电路生产工艺的要求，对喷印机的重量提出了较为苛刻的要求。目前，国外印制电子喷印产品重量只有国内同类产品的60%左右。为了降低生产成本，提高产品竞争力，使喷印机具有较小重量的同时保证整机打印精度，已成为国内印制电子喷印产品设计的迫切需求。

喷印机喷头与大理石平台上基材间的相对位置变化是影响打印精度的主要因素，即喷印机的刚度决定着整机打印精度，对喷印机进行轻量化设计实际上是在减重过程中满足其刚度要求的多目标优化设计问题。目前，对于多目标优化问题，多目标遗传算法(Multi-objective Genetic Algorithm，MOGA)[3]能快速有效地获得Pareto最优解集，如李楠[4]等利用多目标遗传算法对水陆两栖机器人结构参数进行优化，并通过样机的各项性能试验，验证了多目标遗传算法在机器人结构设计中的适用性。王平[5]等采用试验设计方法结合多目标遗传算法来进行车身结构优化，可以控制系统的不确定性因素，保证最终优化结果的可靠。

简要介绍了多目标遗传算法与响应面法，制定了喷印机结构轻量化设计路线，以喷印机重量和刚度为优化目标，利用多目标遗传算法，基于ANSYS Workbench协同仿真平台，通过调整和优化其结构参数，实现产品轻量化设计。

1 多目标优化算法

1.1 多目标优化问题

在实际工程优化设计过程中，优化问题往往涉及多个设计指标，即多目标优化问题。其中各优化目标之间常常是相互联系、制约的，一个目标性能的提升往往会降低其他目标的性能，因此一般不存在一个最优解使所有指标达到最优，而是通过求解得到由多个最优解组成的集合，称为Pareto最优解集(非劣解)。这些最优解之间对于优化指标而言是无法进行比较的，需要决策者根据设计要求和工程经验，通过协调与折中处理，从中选出一个或多个解来当作问题的最优解[6]。

对于印制电子喷印机结构优化问题，在轻量化设计过程中需要满足其刚度要求，但增强结构刚度和减轻结构重量这两个目标之间相互冲突，因此喷印机的优化设计就是找出重量与刚度这两个对立目标最佳平衡点的多目标优化问题。

1.2 多目标遗传算法

多目标遗传算法将生物进化理论应用在现代优化问题上，可以在一次的优化过程中，搜索到大量的多目标优化问题Pareto最优解，是一种高效并行且鲁棒性好的全局优化方法。

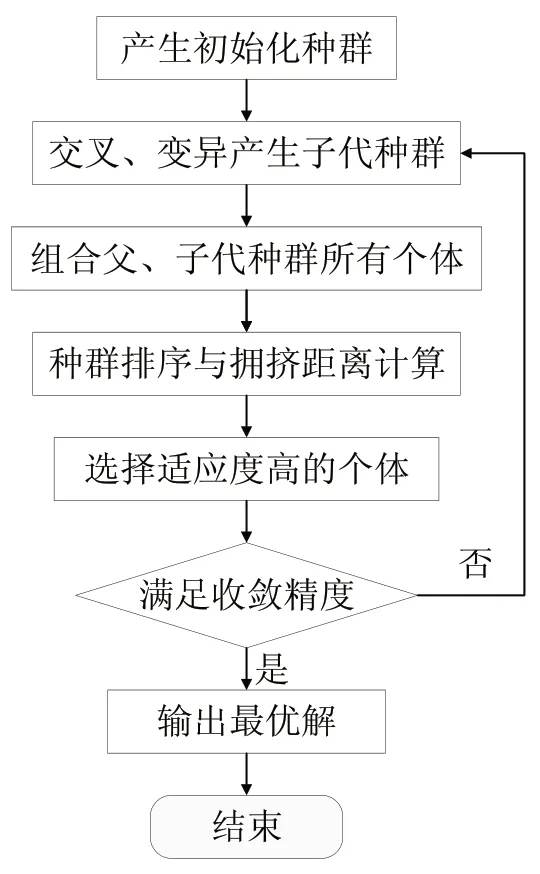
图1 多目标遗传算法流程图

多目标遗传算法将优化问题可行域中的解看作种群中的个体，并编译成编码符号串，对种群中的个体进行选择、交叉及变异操作，通过种群排序和拥挤距离计算，以适应度为依据，种群内的个体一代代进化，逐渐逼近最优解[7]。其基本优化流程如图1所示。

2 响应面方法

响应面法(Response Surface Methodology,RSM)[8]对指定设计点集合进行试验设计，通过构造显式近似表达式将涉及设计变量的目标与约束隐式函数替代为显示函数关系，从而得到响应面模型来预测非试验点的响应值。本文选用准确性较高的完全二阶多项式响应面模型，对于n个设计变量可表示为：

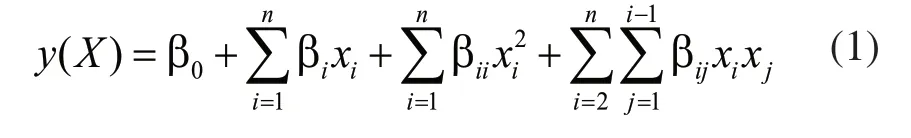
对于生成的响应面模型，采用拟合优度(Goodness of Fit)来评价其对试验设计数据的拟合程度，通常用复相关系数R2表示，其数值在[0,1]变化，且越接近1，说明误差越小，即响应面越准确。

3 轻量化设计

3.1 喷印机结构轻量化设计流程

基于多目标遗传算法的印制电子喷印机结构轻量化设计思路如下：首先，根据喷印机结构，明确影响优化指标的关键因素，在NX 7.0平台建立三维参数化模型，通过CAD与CAE软件间的无缝连接接口，将参数化模型导入ANSYS Workbench并进行有限元分析，为后续的优化设计提供依据。然后选用中心复合试验(Central Composite Designs,CCD)[9]来确定试验点，并进行有限元分析计算，通过这些试验点数据建立响应面模型。接着，运用转移哈默斯利(Shifted Hammersley)序列抽样技术抽取样本点，当作多目标遗传算法的初始种群。最后，通过多目标遗传算法，得到轻量化设计的最优解。具体喷印机结构轻量化设计流程如图2所示。

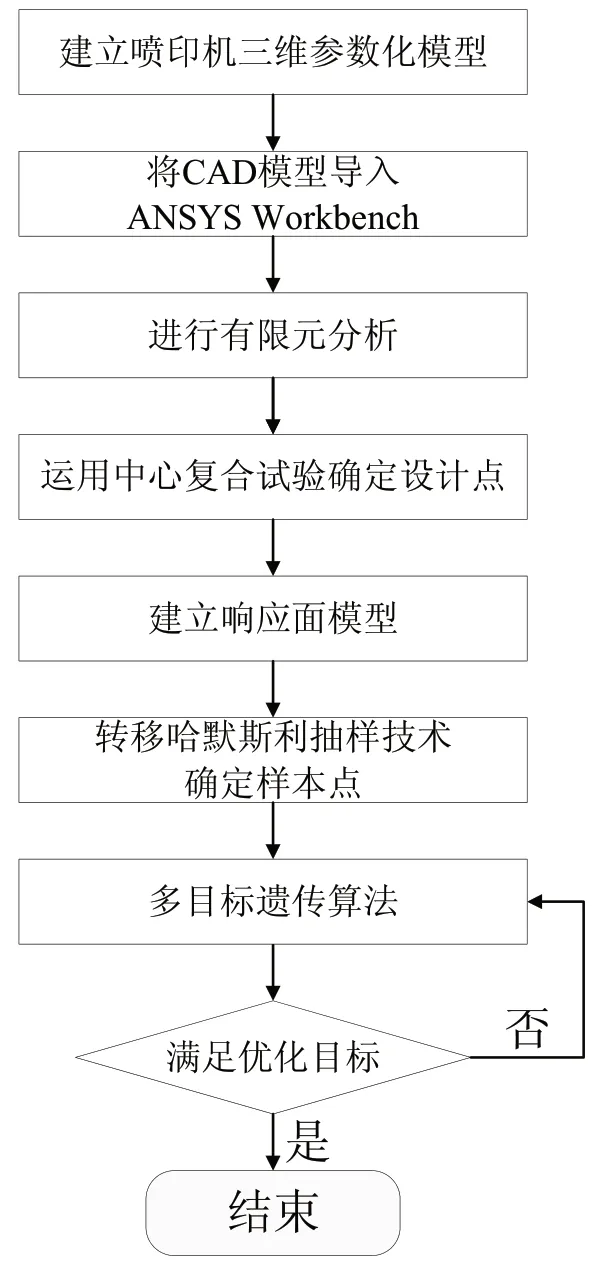
图2 喷印机结构轻量化设计流程图

3.2 喷印机结构有限元模型

通过建立喷印机结构的有限元模型并进行分析，可以得到其稳定性与刚度特性，明确结构的薄弱环节，为后续的轻量化设计提供依据。

1）三维参数化模型的建立

印制电子喷印机机械结构主要分为床身、工作台及基座三部分，如图3所示。喷印机共有三个方向运动：X向为含有喷头的Z模组工作运动；Y向为放置基材的工作台运动；Z向为喷头上下运动，用于调整基材的厚度。

为提高分析效率、改善网格划分质量，需要简化或去除模型中对分析结果影响较小的零部件或细节特征（如工艺孔、倒角等）。

采用NX 7.0建立喷印机简化后的三维参数化模型，完成后通过修改模型中的关键尺寸参数名称(加前缀“DS_”)，将其导入ANSYS Workbench的Design Modeler模块中，实现模型与设计变量的无缝连接。建好的三维参数化模型如图4所示。

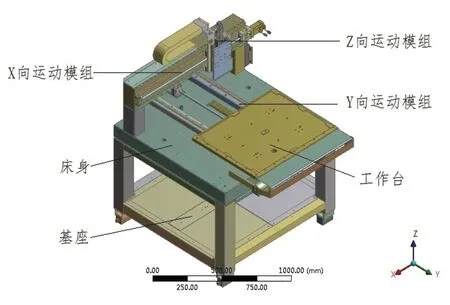
图3 印制电子喷印机机械结构图

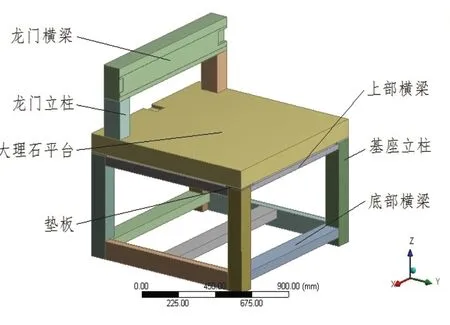
图4 简化后的三维参数化模型

2）载荷与约束处理

运用Mechanical模块进行喷印机机械结构的静力学有限元分析。大理石平台、龙门横梁及两个立柱采用济南花岗石，垫板与基座采用结构钢。零部件之间采用默认的绑定接触方式。由于ANSYS Workbench有着强大的智能网格划分功能，采用默认网格划分，单元尺寸设置为30mm。整个结构依靠四个基座立柱的底面支撑，故对四个底面进行固定约束。该打印机的受力情况比较复杂，但对于整机刚度影响较大的是X模组与Y模组的负载，因此重点对龙门横梁和大理石平台进行受力分析，其中龙门横梁承载的总重约为15Kg，在受力面加力F=150N(g=10N/Kg)，大理石平台承载的床身的负荷约为50Kg，加力大小为F=500N(g=10N/Kg)，方向均为-Z。载荷与约束如图5所示。

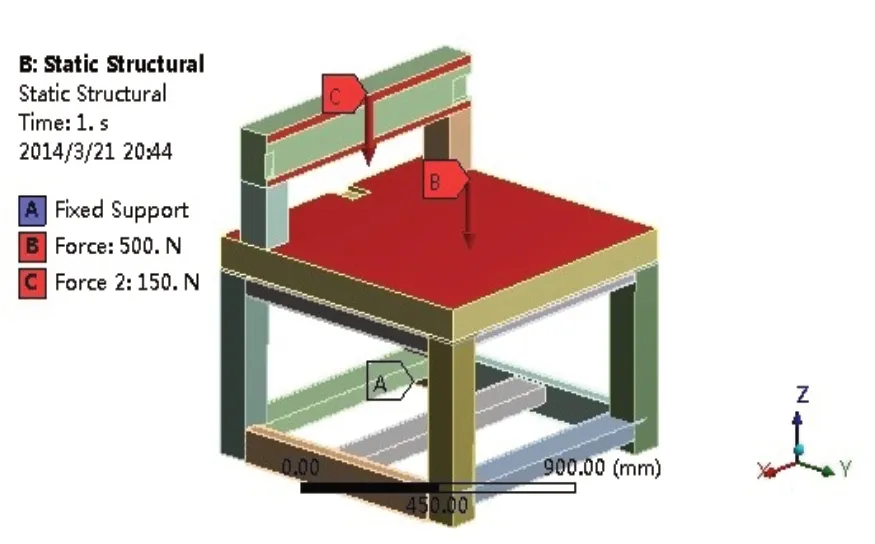
图5 结构的载荷与约束

3）有限元分析结果

将结构的总变形设置为输出结果，求解结果如图6所示。从图可知，最大变形为0.0028mm，出现在龙门横梁中上部位置且呈现绕X轴的扭转变形，大理石平台中间部位向下变形，其余零部件的变形较小，故整个结构具有较大优化空间。

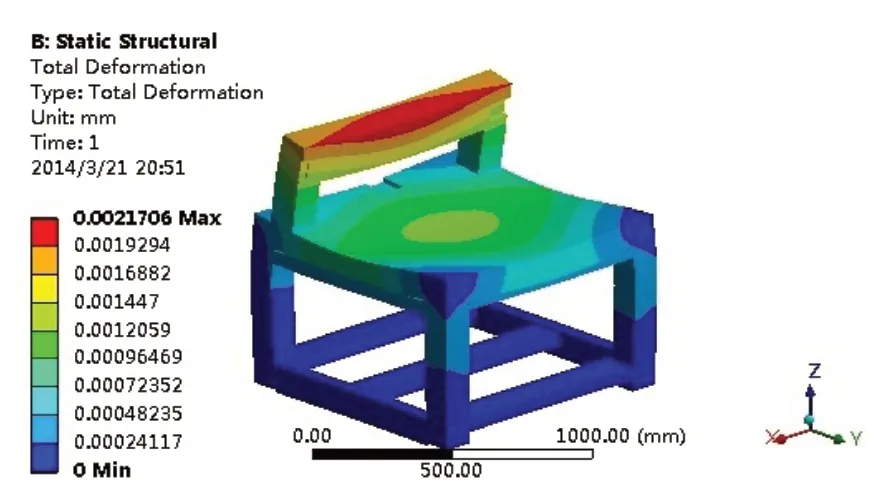
图6 床身的变形云图

3.3 喷印机多目标优化数学模型

以喷印机结构主要零部件尺寸及其之间的距离为设计变量(取值范围在设计变量的10%左右)，提取的设计变量如表1所示。以降低喷印机重量和提高结构刚度为双优化目标，其中提高结构的刚度即减小结构最大变形。

具体的喷印机多目标优化设计数学模型描述如下：

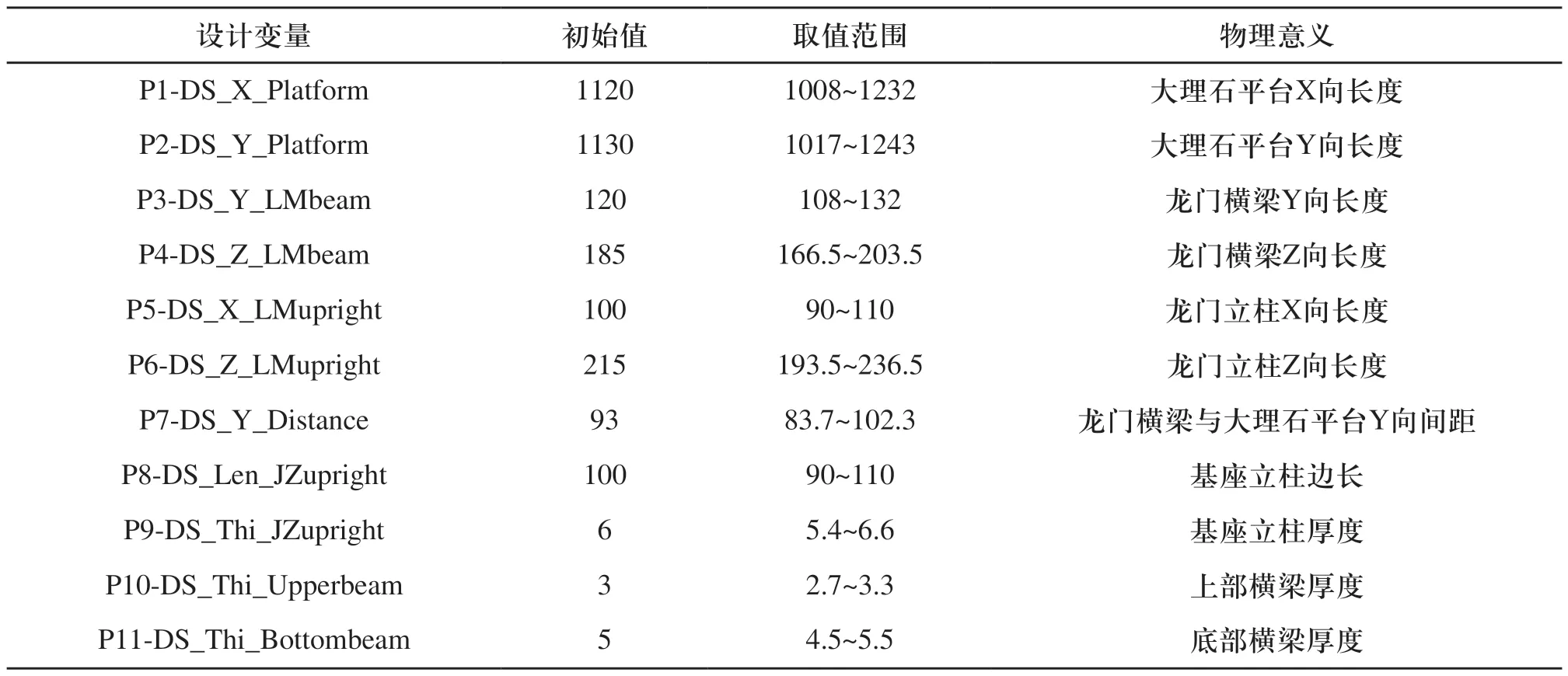
表1 床身关键结构设计参数（mm）

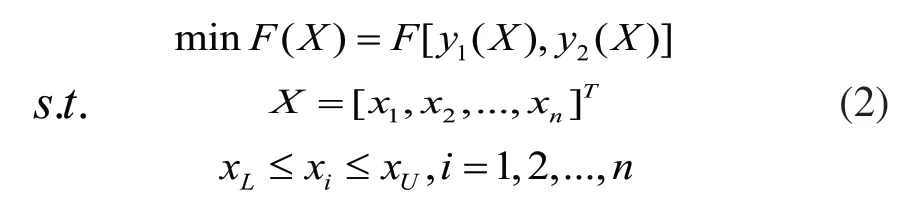
式中，y1(X)为喷印机结构重量，y2(X)为结构最大变形，X为决策向量，xL、xU分别为设计变量的下限值和上限值。

3.4 优化过程与分析

通过实验设计DOE中的中心复合试验设计生成151个试验点及其有限元分析响应结果，再通过二次插值函数生成响应面与局部灵敏度模型。采用拟合度曲线来评价响应面拟合优度，如图7所示，重量和最大变形样本点均在对角线附近，表示响应面拟合优度较高。

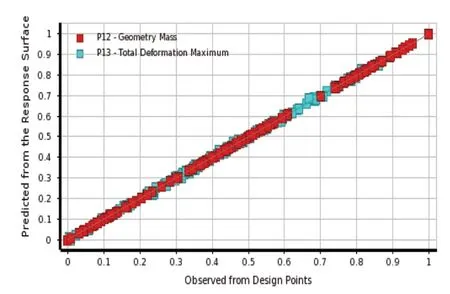
图7 拟合度曲线

生成的响应面与局部灵敏度模型如图8、图9所示。由图8可知，大理石平台X向长度P1与Y向长度P2对结构重量影响最大，这是因为大理石平台的尺寸对喷印机结构的整体大小起决定性作用。

图8 响应面

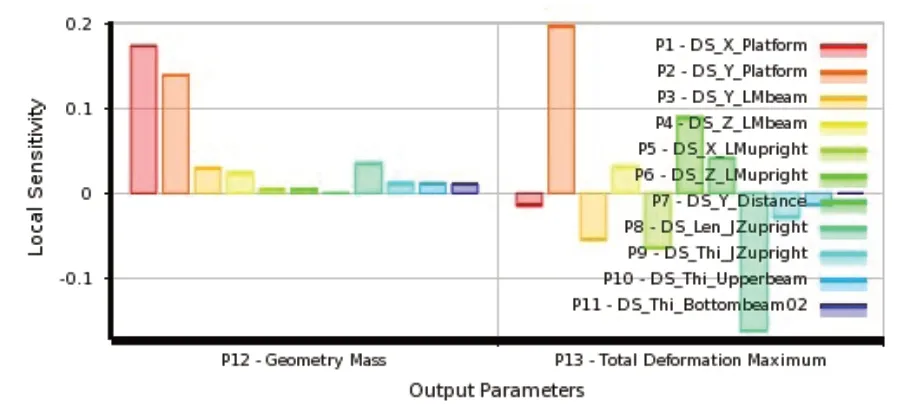
图9 局部灵敏度

图9灵敏度分析说明了对结构刚度影响较大的是大理石平台Y向长度P2，龙门立柱Z向长度P6次之，另外，由于基座立柱采用空心结构，基座立柱边长P8对结构刚度有负面影响。

利用多目标遗传算法(MOGA)对目标函数优化求解，设定初始样本数为100，最大迭代次数为20，收敛准则为70%，结构重量与最大变形的权重大小一致，经过计算得到Pareto最优解集[10]，如图10所示。

表2 关键结构设计参数优化前后值(mm)

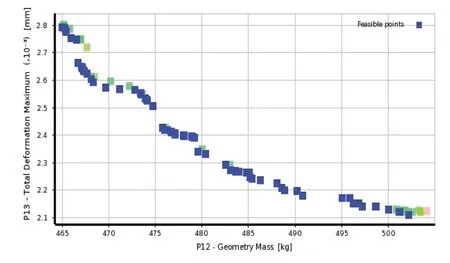
图10 重量与最大变形最优解集

由图可知，可行解位于坐标系原点附近，这符合优化目标最小化期望。从最优解集中选取效果较好的一组作为最优解，并以其为设计点验证优化后的效果。优化前后与圆整后结果如表2、表3所示。

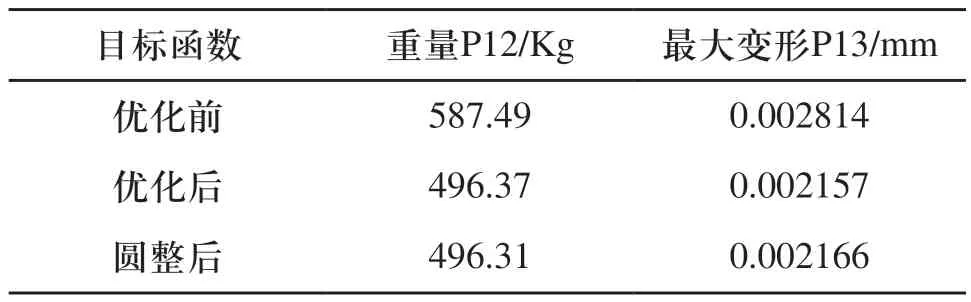
表3 优化前后结果对比

从表3可以看出，优化并经圆整后的结构重量为496.31Kg，比优化前降低了15.5%；而最大变形为0.002166mm，比优化前减小了23.3%，喷印机的结构性能得到较大提升，满足了产品轻量化设计要求。

4 结论

基于协同仿真平台ANSYS Workbench，以减轻印制电子喷印机重量和提高结构刚度为目标，采用多目标遗传算法对喷印机的机械结构参数进行了优化设计，优化后的结构重量比优化前减小了23.3%，实现了喷印机的轻量化设计要求，为结构的优化设计提供了参考依据；

采用多目标遗传算法，能够实现全局搜索寻优，在可行域内快速准确地获得喷印机结构轻量化设计问题的Pareto最优解集，提高了多目标优化设计效率。

[1]龚永林.印制电子综述(2)[J].印制电路信息,2009(8):12-17.

[2]程伟.印制电子喷墨打印机力学性能分析与结构优化[D].上海:华东理工大学,2013:1-7.

[3]Fonseca C M,Fleming P J.Multi-objective Optimization and multiple constraint handling with Evolutionary algorithms-part I:A unified formulation[J].IEEE Transactions on Systems,Man,and Cybernetics,Part A:Systems and Humans,1998,28(1):26-37.

[4]李楠,王明辉,马书根.基于多目标遗传算法的水陆两栖可变形机器人结构参数设计方法[J].机械工程学报,2012,48(17):11-20.

[5]王平,郑松林,吴光强.基于协同优化和多目标遗传算法的车身结构多学科优化设计[J].机械工程学报,2011,47(2):102-108.

[6]于海莲,王永泉,陈花玲.响应面模型与多目标遗传算法相结合的机床立柱参数优化[J].西安交通大学学报,2012,46(11):80-85.

[7]虞召源.高速精密自动光学检测机的结构分析与优化[D].广州:华南理工大学,2012:31-36.

[8]BEYENG D Y,KYUNG K C.A new response surface methodology for reliability-based design optimization[J].Computers &Structures,2004,82:241-256.

[9]Mehdi Asadollahzadeh,Hamed Tavakoli,Meisam Torab-Mostaedi,et al.Response surface methodology based on central composite design as a chemometric tool for optimization of dispersive-solidification liquid-liquid microextraction for speciation of inorganic arsenic in environmental water samples[J].Talanta,2014,123:25-31.

[10]Deb K.,Partap A.,Agarwals S.,et al.A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.