工业机器人运动学逆解的几何求解方法

黄晨华

HUANG Chen-hua

（韶关学院 物理与机电工程学院，韶关 512005）

0 引言

工业机器人的运动学是工业机器人控制与轨迹规划的基础，其内容包括正运动学和逆运动学。当给定机器人所有关节转过的角度时，可以通过机器人的正动学方程来确定其末端操作器的位解；当已知机器人末端操作器的位置时，则可根据运行学逆解获得各关节需转过后角度。机器人运动学建模的标准方法，即D-H建模，可以很方便地得到机器人的正运动学方程，而要获得机器人的逆运动学方程，则难度较大，求解的方法可以分成两大类：数值解和封闭解。Tsai[2]等研究了通用的6自由度和5自由度的机械臂的数值解，Nakamura[3]等研究了适用了机器人控制的带有奇点鲁棒控制的数值逆解，Baker[4]等研究了冗余机械臂的数值逆解，数值解的最大不足就是计算时比较耗时，对系统造成较大的负担。封闭解是基于解析形式的解法，其又可分为代数法和几何法，用代数法求逆解在很多机器人经典教材和文献中都有详细的论述[5～7]，在此不作具体讨论，刘达[8]等为了使机器人获得更好的实时性，提出了一种解析和数值相结合的机器人逆解算法，陈庆诚[9]等提出基于旋量理论的逆运动学子问题求解算法。用几何法求解机器人运动学逆解，则少有文献作详细论述，以5自由度工业机器人为例，对几何法作深入的探讨。

1 机器人结构

机器人有五自由度，最后2关节相交一点，从结构上分析，此机器人存在运动学逆解。机器人的实物图如图1所示，各关节坐标如图2所示。机器人的DH参数如表1所示。

图1 5自由度机器人

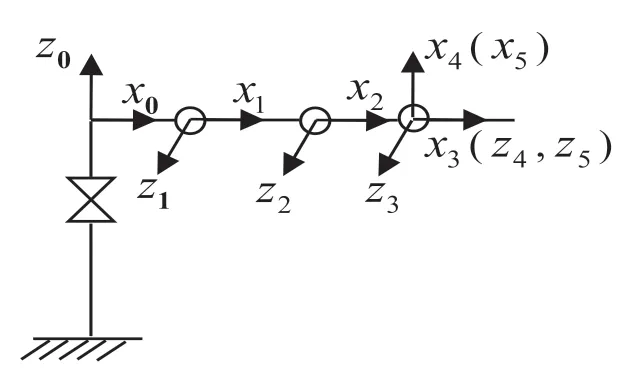
图2 机器人关节坐标设置

表1 机器人DH参数

各关节间的变换矩阵为：

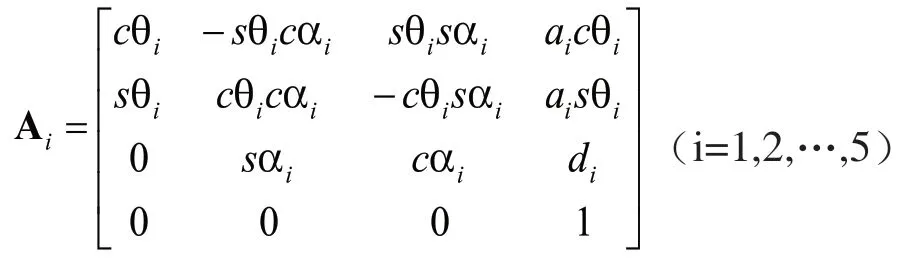
式中，cθi=cosθi，sθi=sinθi。

2 机器人运动学逆解

2.1 几何解法[10]

使用几何法获得机器人逆解的首要条件是机器人存在封闭解，现在机器人在结构上一般都能满足这一要求。求解过程如下：

1)分析机器人各自由度对机器人位姿的影响，即哪些自由度的变化只影响机器人末端操作器的位置，哪些自由度的变化只影响机器人末端操作器的姿态；

2)求机器人的位置逆解方程，忽略对机器人位置没有影响的结构，在机器人的基坐标内求位置逆解方程；

3)求机器人的姿态逆解方程，利用已求解的位置解，通过矩阵变换，可很方便地求出姿态逆解。

2.2 机器人逆解的几何求法

由图2可知，机器人的最后两个关节相交于一点，为计算简便，把机器人的工具坐标也设于此点，且与最后一关节坐标重合。

设末端操作器的位置坐标值为(xe,ye,ze)，姿态用欧拉角表示，其姿态矩阵为：

2.2.1 位置逆解求解

与位置相关关节变量有 θ1，θ2和 θ3，参考机器人结构示意图（如图3所示），分别用几何法求解。

1）θ1求解

机器人的结构投影如图4所示。

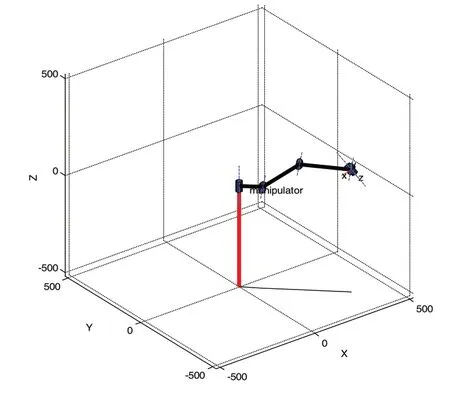
图3 机器人结构示意图

图4 关节1在x0-y0平面的投影

由图4可得：

或：

2）θ2，θ3求解

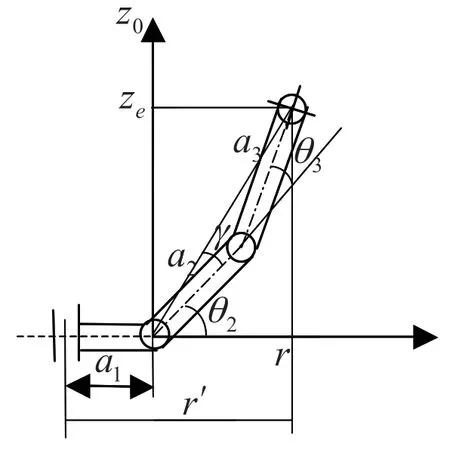
图5 关节2、3在z0-r平面的投影

由图5中的几何关系，可得：

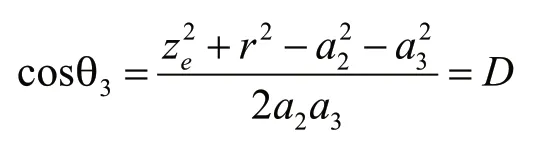
则有：

因此：

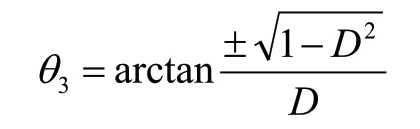
同理：

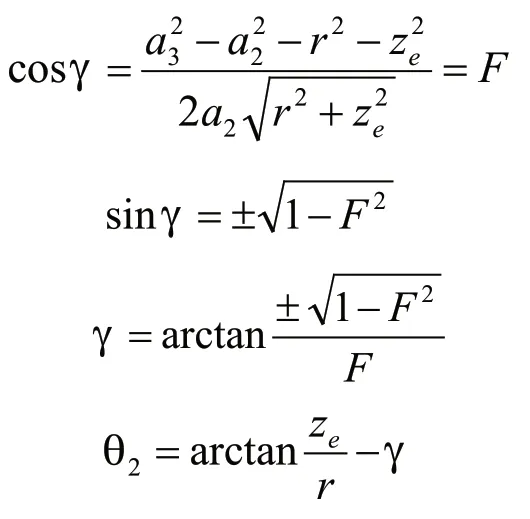
2.2.2 姿态逆解求解

由各关节的变换矩阵有：

因 θ1，θ2，θ3已求得，且T为已知，对上式进行变换，有：

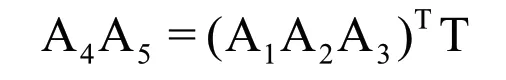
因篇幅有限，具体推算过程略，计算结果如下：

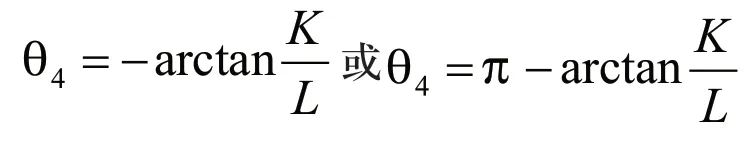
式中：

式中：

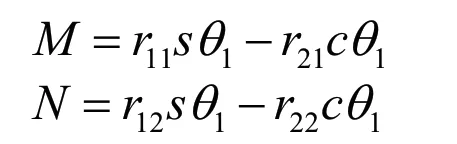
3 仿真验证

假设机器人各关节的转动不受任何限制，首先设各关节的转动任意角度，具体数值如表2所示，利用机器人正运动学方程，获得机器人末端操作器的位置和姿态，然后此位置和姿态，用所求得的逆解方程求各相应的转角，看与预先假设的各关节的转角是否相等。从表3的数值可以得出，用几何法所获得的机器人逆解是正确的。需要说明的是为了仿真程序编写简单，仿真的数据均限制在[0,1]之间，但不影响结论的正确性。

表2 各关节转角假设值(rad)

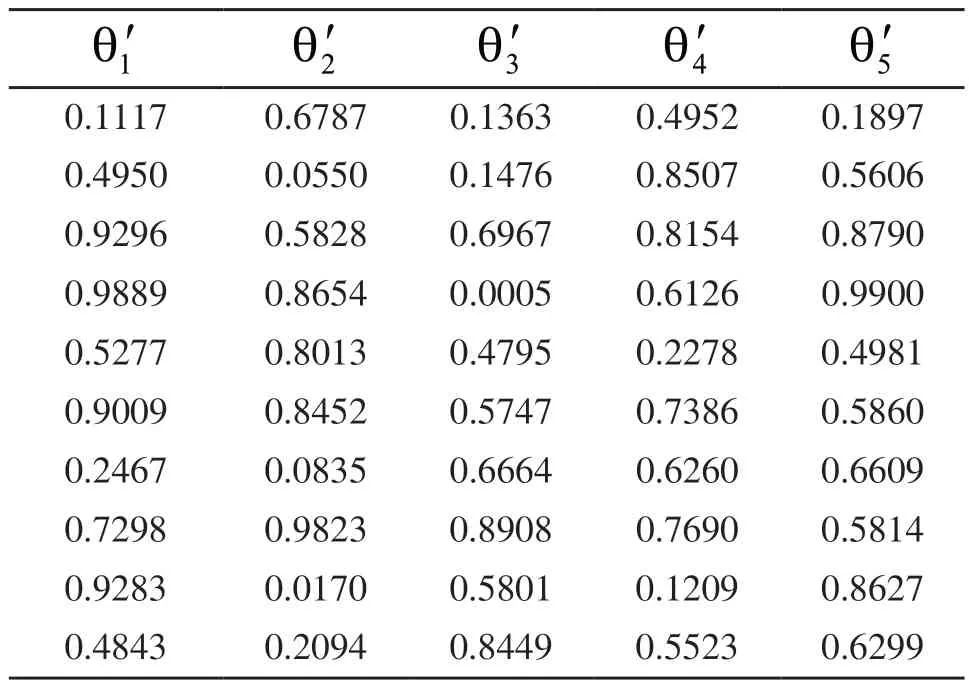
表3 逆解方程所求得的各转角(rad)

4 结论

针对工业机器人运动学逆解求解的问题，以5自由度机器人为例，深入探讨了几何法求逆的方法和过程，并以仿真的手段验证了方法的可行性。从求解过程中，可得出几何法求逆具有以下特点：1)直观、简便，只需进行简单的几何推导即可获得位置逆解；2)计算量小，姿态逆解只需一步矩阵运算即可求得。

[1]Denavit,J.,R.,Hartenberg S..A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices[J].ASME Journal of Applied Mechanics,June 1955,215-221.

[2]Tsai L.,Morgan A..Solving the Kinematics of the Most General Six-and Five-degree-of-freedom Manipulators by Continuation Methods[A].ASME Mechanisms Conference[C].Boston,Oct.7-10,1984,84-DET-20.

[3]Nakamura Y.,Hanafusa H..Inverse Kinematic Solutions with Singularity Robustness for Robot Manipulator Control[J].ASME Journal of Dynamic Systems,Measurement,and Control,1986,108.

[4]Baker D.,Wampler C..On the Inverse Kinematics of Redundant Manipulators[J].International Journal of Robotics Research,1988,7(2).

[5]Saeed B.Niku.Introduction to Robotics Analysis,Control,Applications(Second Edition)[M].Beijing,Publishing House of Electronics Industry,2013,3:66-70.

[6]John J.Craig.Introduction to Robotics Mechanics and Control(Third Edition)[M].Beijing,China Machine Press,2013:83-86.

[7]王战中,杨长建,刘超颖,等.MATLAB环境下六自由度焊接机器人运动学逆解及优化[J].机械设计与制造,2013(7):182-184.

[8]刘 达,王田苗.一种解析和数值相结合的机器人逆解算法[J].北京航空航天大学学报,2007(6):728-730.

[9]陈庆诚,朱世强,王宣银.基于旋量理论的串联机器人逆解子问题求解算法[J].浙江大学学报(工学版),2014(1):8-14.

[10]Lee C.S.G.,Ziegler M..Geometric Approach in Solving Inverse Kinematics of PUMA Robots[J].IEEE Transactions on Aerospace and Electronic Systems,1984,AES-20(6).