穿孔板声特性的数值模拟和试验研究

宁玉恒，杨 丹

NING Yu-heng1, YANG Dan2

（1.大唐东北电力实验研究所有限公司，长春 130021；2.吉林农业大学，长春 130118）

0 引言

在噪声控制工程中，穿孔板共振结构是一种常用的吸声结构[1]，目前已广泛应用于高速列车和客车的顶部以及发动机的消声器中[2]。对穿孔板吸声结构的研究目前主要集中在理论和试验阶段，马大猷推导了穿孔板吸声结构的理论[3]，刘克从试验着手研究了扩散场内穿孔板的吸声特性[4]，在穿孔板声辐射效率方面的研究几乎处于空白。

现阶段对穿孔板进行数值仿真的研究相对比较少，在理论和试验比较成熟的情况下，数值模拟可以节约时间，降低成本。拟采用边界元方法对穿孔板的隔声性能进行仿真，并与试验进行对比，验证了此种方法的可行性。穿孔板声辐射效率已无法使用传统的声振法测试，鉴于此，尝试采用单元分离法进行测量，单元分离法在工程中的应用也很少，李民等人使用单元分离法测量发动机齿轮罩的声辐射效率[5]。最终结果表明，通过单元分离法可以准确获得穿孔板的声辐射效率。

1 穿孔板有限元模型的建立

穿孔板的尺寸是840mm×7000mm×1.7mm，由于较薄，采用三维建模会影响网格质量，因而采用壳单元划分网格，然后赋予结构厚度。由于孔的尺寸相对截面尺寸很小，建模时，如果对小孔进行处理，网格质量将会降低，计算精度难以保证，因此，在划分网格时，将所有孔密封处理，通过赋予导纳属性来模拟小孔，有限元模型如图1所示，共有167964个壳单元。

图1 穿孔板的有限元模型

2 阻尼损耗因子测试

结构动力学特性的影响因素除了系统的质量和刚度，还有阻尼损耗因子。为了获取穿孔板的阻尼损耗因子，试验采用脉冲衰减法[6,7]进行了测试，测试装置示意图如图2所示，将穿孔板用柔性绳悬挂，满足构件受激后自由振动[8]。选取合理的位置布置六个振动加速度传感器，用力锤在多个位置进行瞬态激励，记录各测试点的振动衰减过程，最后结合先进的数据处理方法，识别得到穿孔板的阻尼损耗因子，如图3所示，穿孔板在1000Hz以内的内损耗因子为0.15%～0.35%。

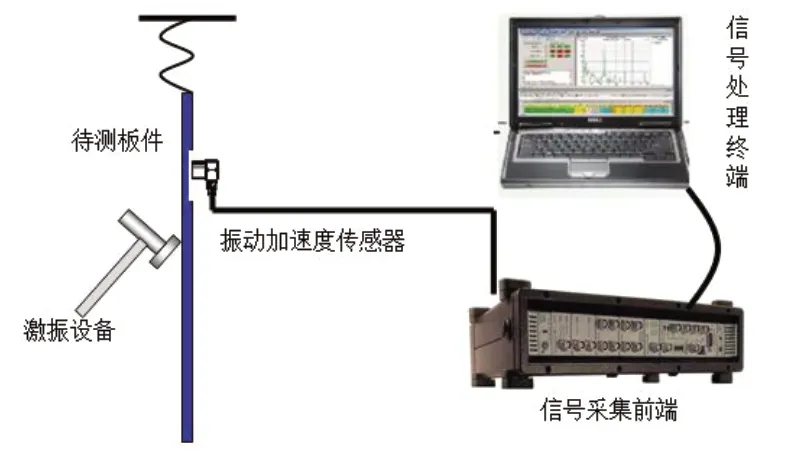
图2 阻尼损耗因子测试示意图

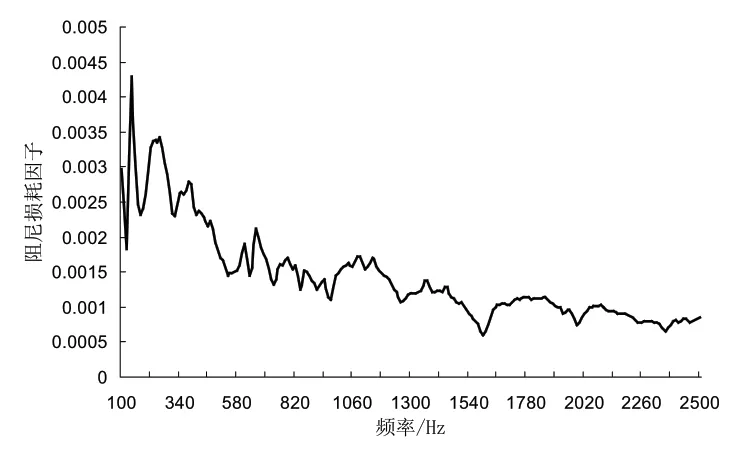
图3 穿孔板的阻尼损耗因子

3 导纳的求解

如上所述，穿孔板在声学计算时，由于存在很多小孔，使得有限元网格的划分非常困难，如果把网格划分得非常细致，那么网格的数量会非常巨大，同时网格质量也会非常差，以至于不能计算。为了解决小孔的问题，在穿孔板两边的网格之间通过定义传递导纳来模拟这些小孔。

声阻抗的表达式为：

式中，Δp 是声音通过穿孔板前后的声压差；υ是小孔处的振动速度。我们能通过Mechel公式来计算得到阻抗ZP。Mechel公式如下所示：

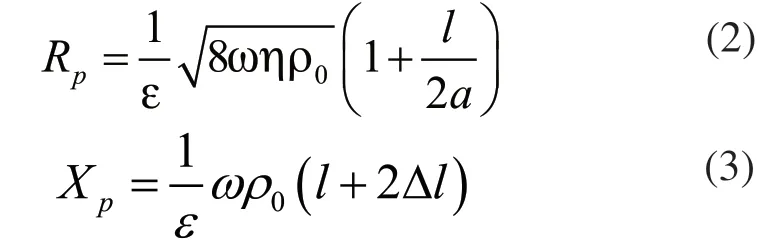
孔隙率ε表示如下：

式中，n 为圆孔的个数；a 为圆孔的体积；S为穿孔板的横截面积；t为穿孔板的厚度。

在工程实际中，圆孔的排列方式主要有正方形和正六边形两种排列方式。文中所述的圆孔排列方式是长条形排列的，但是康钟绪等人研究表明，圆孔的排列方式对修正厚度的影响很小[9]，因此可以借鉴正方形排列方式的计算公式获得修正厚度：

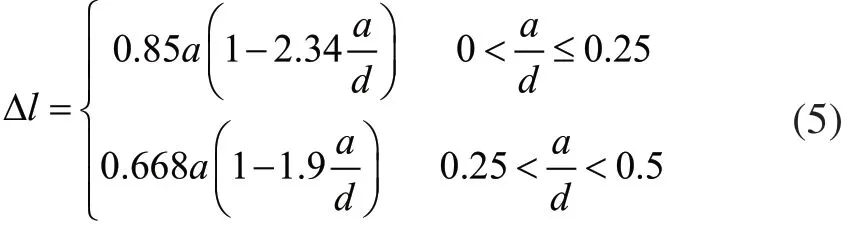
式中，d为两相邻圆孔中心的距离。

在Virtual.Lab声学计算软件中，穿孔板是通过定义一个传递导纳矩阵来表示的，该矩阵如下：

其中，系数k考虑了穿孔板的厚度对穿孔板两侧面积的影响，即k为穿孔板上下截面积的比值，在文中可以取1；。

进行声学计算时，由于不同频率下传递导纳的数值不一样，因此我们需要获得一系列的导纳值。穿孔板两侧的振动速度和声压的传递导纳关系用以下公式来表示：

其中，υ1n和υn2是穿孔板两侧的法向振动速度；p1和 p2为穿孔板两侧的声压；α1、α2、α4、α5为传递导纳系数，其值就是上式的矩阵，前文表明，系数k取1，因此 α1=α5，α2=α4，α3和 α6是由声源确定的，在试中均为0，因此只要计算出导纳，就可以知道振动速度和声压的关系，进一步获得其他声学参数。

将各个参数代入上式中，可以获得各频率下的导纳值，导入软件进行计算。

4 穿孔板的隔声量数值计算和对比

由于穿孔板孔径较小，结构网格较为密集，采用有限元法计算量较大且比较费时，因此采用间接边界元法进行数值计算。仿真模型如图4所示，利用12个平面波作为混响激励声源，定义障板模拟试验环境的刚性墙面，在入射侧定义边界元网格属性为透明单元，用于接收声激励，透射侧边界元网格与结构网格耦合，场点网格用于接收透射侧的声功率。将上述试验测试的阻尼损耗因子和数值计算的传递导纳导入到模型中去，进行计算，获得穿孔板两侧的入射声功率和透射声功率，最后将入射和透射声功率相除，就可以获得穿孔板的隔声量。仿真边界条件的选取尽量接近实际状态。

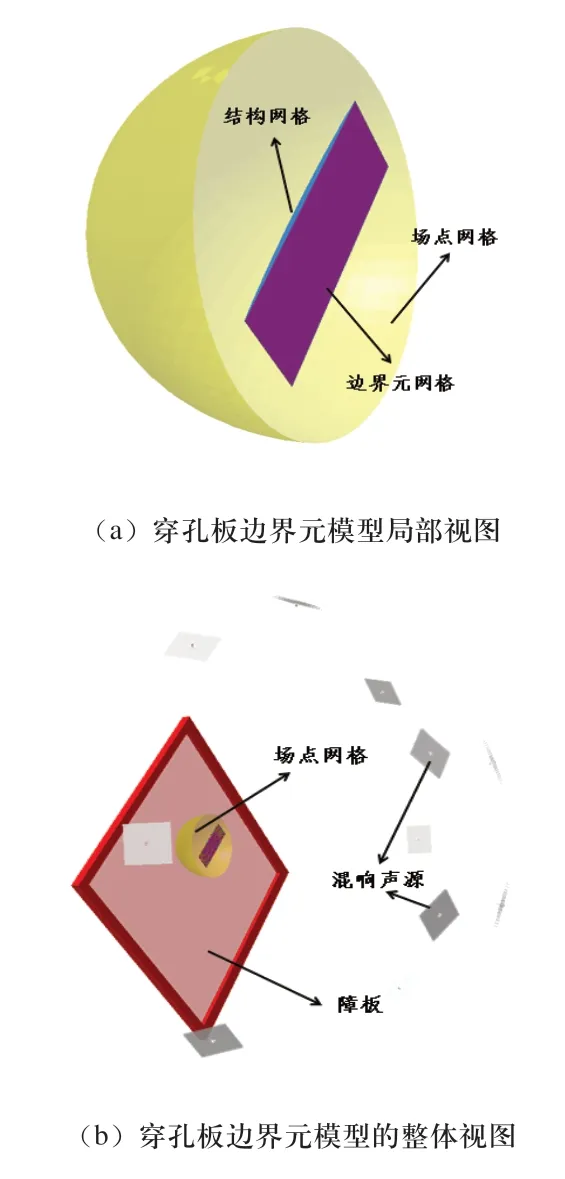
图4 穿孔板的仿真模型

将使用边界元方法计算的仿真隔声量与试验值进行比较，结果如图5所示。

图5 隔声量的仿真与试验比较

从图5中可以看到，在160Hz以下的低频范围内，隔声量试验与仿真结果不仅在数值上相差比较大，变化趋势也相反，主要因为该频段内的隔声性能主要由边界条件确定，实际约束状态比较复杂，使得仿真时很难准确地模拟，以至于结果相差比较大，超过160Hz，试验与仿真在变化趋势和数值上都很接近，总体而言，此种方法可以用来准确地预测穿孔板的隔声性能。

5 声辐射效率测试

结构振动所辐射的声音是噪声的主要来源之一。它通过结构振动，从而引起结构周围流场的波动将能量传播出去。

薄板结构在各个领域应用很广泛。然而，由于其刚度较小，在工程应用中容易产生振动，从而辐射噪声，成为噪声源。因此，研究板件的声辐射特性对于如何有效控制板件的结构形式、连接方式，从而改变结构的声辐射特性，以获得期望的结构的声辐射特性就显得非常重要而有意义了。

目前对声辐射特性的研究主要基于声强法，即通过结构辐射声场的结构包络面S上的声强，通过声强In与结构包络面的乘积获得结构的辐射声功率∏，如式（8）所述：

但是，声强法对测试环境很敏感，使得试验往往只能在消声室内进行，这样成本较高，而且局限性很大。因此，对于工程实际的现场测量来说，声强法并不能满足测试要求。而且穿孔板上面存在很多小孔，使用传统的声振测试方法，会从小孔中漏声，导致测试结果不准确，在此尝试使用一种新的测试方法，即分离单元法。

对于活塞运动的声辐射结构有：

如图6所示，将板件离散成一系列矩形的振动单元，单元尺寸取决于研究的频率范围。将每一个振动单元视为一个小的振动活塞。通过求解每个单元的辐射声功率，最终可以求得结构总的辐射声功率。

图6 板件振动单元划分示意图

依据上述思想，将穿孔板划分为14×15个单元，每次采用五个振动传感器测量振动速度。

单元i的自辐射阻抗Rii为：

单元i和单元j之间的互辐射阻抗Rij为：

式中，ρ为空气的密度，c为空气中的声速，Si和Sj为单元i和单元j的面积，J1为第一类一阶Bessel函数，为空气中的波数，为圆形单元等效为矩形单元的等效半径，为虚数单位，S1为Struve function，dij为单元i和j的距离，如图6所示。

根据单元的辐射阻抗可以求得单元i 的辐射声功率∏i为：

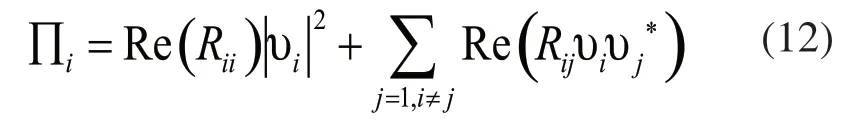
式中，Re表示取实部，υi为单元i表面的法向速度。*表示共轭复数。将所有单元的辐射声功率求和即可求得板件的辐射声功率。

由式（12）可见，只要测得单元表面的法向速度，即可方便地求得结构的辐射声功率。由于只需测量结构的振动速度而不用测声强或者声压，也不存在漏声的状况，所以该法具有更高的精度，而且也有更广的适用性。

由于已经获得结构表面的振动速度和辐射声功率，因此不难获得结构的辐射效率σ：

通过分离单元法测试的声辐射效率如图7所示。

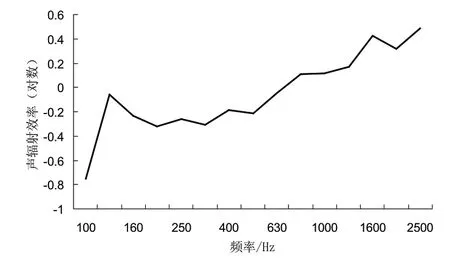
图7 穿孔板的声辐射效率

穿孔板的厚度只有1.5mm，致使其吻合频率很高，图中测试的频率上限并未达到吻合频率。声辐射效率在吻合频率以下，总体上会呈现出上升的趋势，这与图中的测试结果吻合，因此表明该种测试方法应用于穿孔板在一定程度上是可行的。

6 结束语

1)使用脉冲衰减法测试了穿孔板的阻尼损耗因子，数值上在0.15%～0.35%之间。为了获得精确的有限元模型，计算了穿孔板两侧的传递导纳。

2)将阻尼损耗因子和传递导纳赋予穿孔板的边界元模型，获得隔声量的仿真值，与试验结果进行对比，总体趋势上吻合良好，验证此种仿真方法可以用来准确预测穿孔板的隔声性能。

3)避开传统声振法在测试穿孔板声辐射效率的不足，采用分离单元法进行测试，测试结果可靠，表明此种方法应用于穿孔板声辐射效率的测试在一定程度上是可行的。

[1]盛胜我.穿孔板背面紧贴吸声薄层时的声学特性[J].声学技术,2003,22(1):52-54.

[2]王占学,乔渭阳,李文兰.微穿孔板消声器在 MA60 飞机APU 排气管的应用[J].航空动力学报,2003,18(3):331-335.

[3]马大猷.微穿孔板吸声结构的理论和设计[J].中国科学,1975,1(1):38-50.

[4]刘克.扩散场内微穿孔板吸声特性的实验研究[J].声学学报,2000,25(3):211-218.

[5]李民,舒歌群,梁兴雨.4100QB 柴油机齿轮室盖声辐射效率试验研究[J].农业工程学报,2011(12):148-152.

[6]Bolduc M,Atalla N.Measurement of SEA damping loss factor for complex structures[J].The Journal of the Acoustical Society of America,2008,123(5):3060-3060.

[7]张红亮,孔宪仁,刘源,等.宽频域的内损耗因子实验辨识方法研究[J].振动与冲击,2013,32(12):179-184.

[8]陈馨蕊,杨陈.镁合金 AZ31 阻尼性能的实验研究[J].浙江大学学报:工学版,2010(1):19-22.

[9]康钟绪,季振林.穿孔板的声学厚度修正[J].声学学报,2009,33(4):327-333.