弹跳机器人弹跳机构的设计与仿真分析

马文硕，米 洁

MA Wen-shuo, MI Jie

（北京信息科技大学 机电工程学院，北京 100192）

0 引言

随着机器人在当今生活中的应用越来越广泛，替代人类发挥的作用日益重要，机器人面临的条件也越来越恶劣，例如救灾、星际探索、军事侦察、考古探测等，这些情形往往具有复杂的地势，需要机器人具有良好的机动能力和越障能力。

地面机器人现有的移动方式多为轮式和履带式，均具有较好的机动能力。而越过与自身大小相当的障碍时，只有弹跳能够做得到。目前实际弹跳机构构造有两类方法[1]，一类是从自然界生物的弹跳动作中获得启发，进行仿造，称为仿生弹跳机构，如机械袋鼠等[2～4]。另一类方式是利用简单机构产生弹力，这种方法机构自由度少，动力学模型简单，实现相对容易。

因此设计一种运用仿生弹跳机构的弹跳机器人，并将其作为后续研究的动力平台。

1 弹跳机器人的弹跳机构设计

跳跃的实质在于质心具有足够快的上升速度[5]，故设计的方案是否可行的关键在于：弹跳机器人跳起的过程中其执行件能否为躯体提供足够大的速度。再而根据动量定理，因为Ft=mv2-mv1，执行件的力越大或执行件与地面间接触时间越长，即冲量越大，自身获得的动量就越大。因此动物以越大的冲量撞击地面，所获得的起跳速度就越大，跳起的高度就越高。

蝗虫具有优秀的弹跳能力[6]，其跳跃具有起跳迅速、腾空持久、落地稳定等优点。当蝗虫的后足的腿节和胫节由褶皱状态突然伸直时，就产生跳跃的动作。在腿节中生有很多斜排的肌肉用来控制胫节的活动，肌肉一端附在腿节的外骨皮上，另一端附着在腿节中一种腱筋的结构上。当腿节内的肌肉收缩时便拉动这条腱筋，使胫节伸直，这时产生相当大的力量撞击地面形成跳跃[7]。蝗虫在起跳阶段释放能量，将弹性能转化为势能和动能；在腾空的下降阶段和着地的压缩阶段，部分动能和势能转化为弹性能，在跳跃过程中很好地进行了能量的转化和平衡。因此本方案采用模拟蝗虫腿部跳跃机理的机构。

在仿生领域中，腱、肌等被科学家认为是昆虫或动物跳跃动作的能量储存和释放机构，也称为弹性储能元件，任何弹簧释放的力都与所储存的能量成正比，与腱筋有较好的仿生一致性。

因此，如图1所示，本方案采用四杆机构近似代替蝗虫各腿[8]，用弹簧BD来模拟蝗虫的腱筋。跳跃前，可通过电机驱动转节A，继而带动大腿LAB转动，拉动弹簧以储存能量。跳跃时，弹簧拉动胫节LBE上端，使胫节LBE绕铰链B瞬间转动，从而在胫节LBE末端，即E点与地面间产生较大的蹬地力使蝗虫实现跳跃。

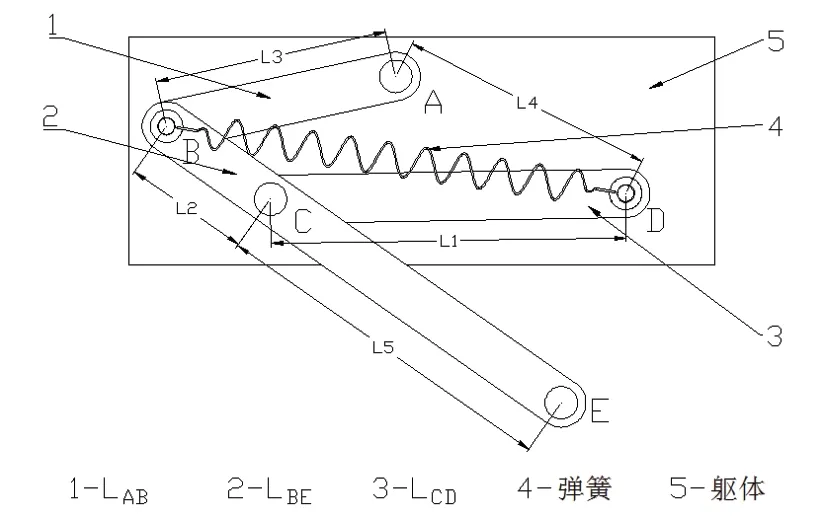
图1 弹跳机器人弹跳机构二维示意图

为控制机身重量，且由于在起跳过程中腿部需要承受较大的冲击力，故要求机身及腿部材料具有较高的韧性和较低的密度，故本方案采用环氧树脂复合板作为样机材料，并选用一台直流电机作为动力源。

图2为弹跳机器人的三维示意图，弹跳机构采用两侧对称的双四杆机构来模拟蝗虫的两条腿，并用一根传动轴将两侧的驱动转节A相连以确保两侧的运动一致性。驱动转矩由电机提供，并经由锥齿轮副将动力传递给传动轴。

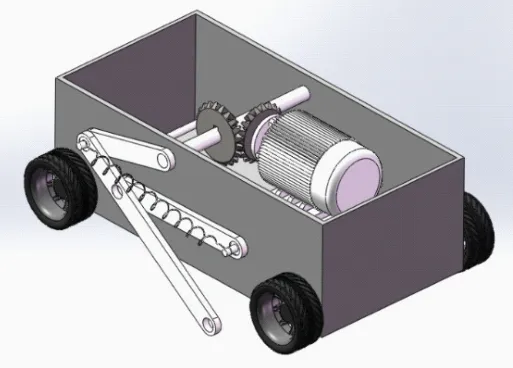
图2 弹跳机器人弹跳机构三维示意图

该方案可通过调节机架杆LAD与水平方向的夹角以适应不同的情况需要，例如：在遇到沙坑等需要跳跃水平距离较大，而对跳跃高度要求不高的情况下，可适当减小LAD与水平方向夹角；在遇到高障碍等需要跳跃高度较大，而对跳跃水平距离不高的情况下，可适当增大LAD与水平方向夹角。

2 基于ADAMS的弹跳机构运动学与动力学分析

2.1 虚拟样机模型的建立

由于虚拟样机技术在进行运动学、动力学求解时，只考虑零件的质心和质量，而对零件的外部形状不予考虑。因此，要对弹跳机构的形态结构进行适当的简化[9]：

1)躯体外形简化为一个长方体。

2)各关节简化为转动副来约束，等效实现二者的相对运动。

3)将两条腿简化为单腿，以便于更好的进行动力学分析。

4)各部件为刚体。

5)忽略关节摩擦。

6)将轮子省略。

根据蝗虫的实际形态结构，按照以上原则，建立了仿蝗虫跳跃机器人虚拟样机模型，如图3所示。其中各参数依次为[10]：L1=105mm,L2=35mm,L3=70mm,L4=77mm,L5=105mm，弹簧刚度K=30N/mm，弹簧原长为115mm，弹簧最大伸长量为55mm，机架LAD与水平方向夹角为153°，初始时刻LAB与水平方向夹角为187°，仿真机构总质量M=3kg。

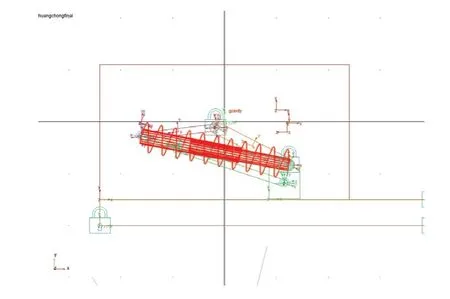
图3 弹跳机器人弹跳机构虚拟样机模型

2.2 基于ADAMS的运动学与动力学仿真

图4中的曲线直观地描述了在跳跃过程中仿真机构质心的运动轨迹。

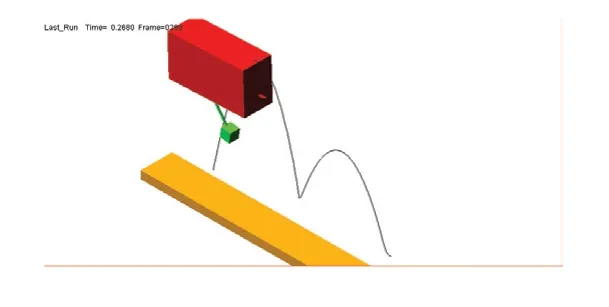
图4 弹跳机器人运动仿真过程

2.2.1 躯体质心运动参数

仿真结果如图5所示，左方曲线为仿真机构质心的运动轨迹，右上曲线为质心在水平方向的位移曲线，右下曲线为质心在竖直方向的位移曲线。

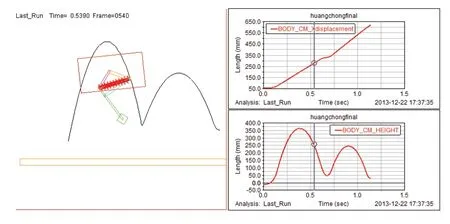
图5 仿真机构仿真结果

图6为仿真机构质心运动水平方向参数，图7为仿真机构质心运动竖直方向参数，其中实线为位移曲线，虚线为速度曲线。

蹬地起跳最大水平位移约为310mm,最大水平速度可达约575mm/s；最大高度可达约360mm，最大竖直速度可达约2300mm/s。受弹簧刚度影响，仿真机构的速度曲线存在少许波动。

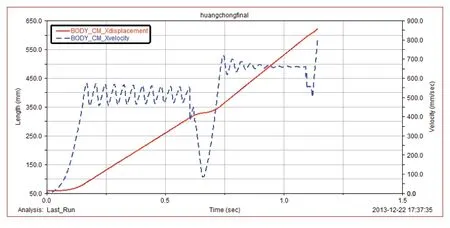
图6 仿真机构质心运动水平方向参数

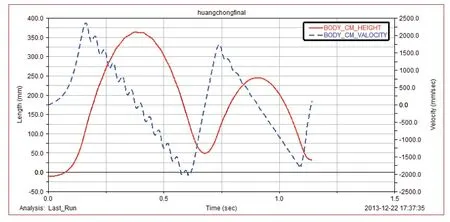
图7 仿真机构质心运动竖直方向参数

为研究机架角度对弹跳机器人跳跃高度和跳跃距离的影响，现将原机构的两个参数做如下改变：机架LAD与水平方向夹角改为128°，初始时刻LAB与水平方向夹角为164°，其余参数不变，再次进行仿真。仿真所得结果如图8所示。

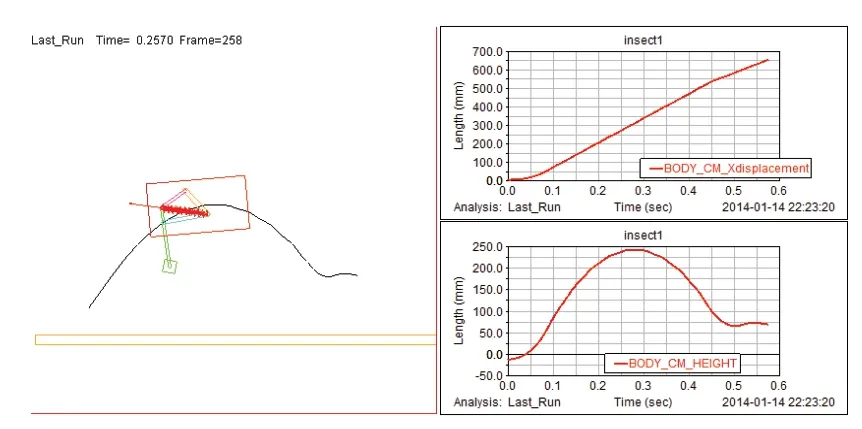
图8 变换机架角度后的仿真结果

图9为变换机架角度后仿真机构质心运动水平方向参数，图10为变换机架角度后仿真机构质心运动竖直方向参数，其中实线为位移曲线，虚线为速度曲线。蹬地起跳最大水平位移约为250mm，最大水平速度可达约1450mm/s；最大高度可达约630mm，最大竖直速度可达约1900mm/s。

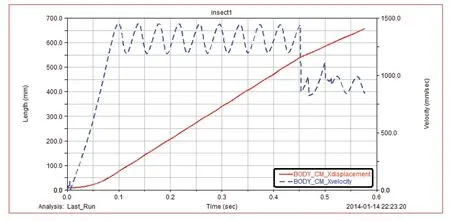
图9 变换机架角度后仿真机构质心运动水平方向参数

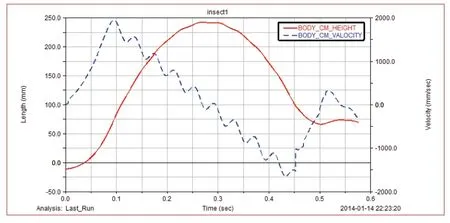
图10 变换机架角度后仿真机构质心运动竖直方向参数

2.2.2 脚部姿态与受力分析

如图11所示，下方曲线为仿真机构脚部（即E点）的轨迹曲线，其中近似直线部分为弹跳时脚部蹬地动作，曲线部分为跳起后的收腿动作。由于蹬地动作非常接近直线，所以该机构在弹跳过程中具有动作平稳，力的传递效率高等优点。

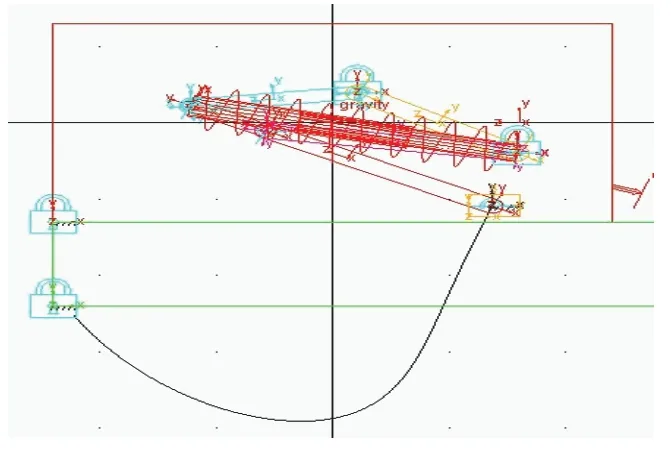
图11 弹跳机构脚部姿态曲线

图12为仿真机构起跳时脚部的受力情况，其中实线为脚部在X方向的受力，虚线为脚部在Y方向的受力，可见X方向最大蹬地力约为29.4N，Y方向最大蹬地力约为141.4N。

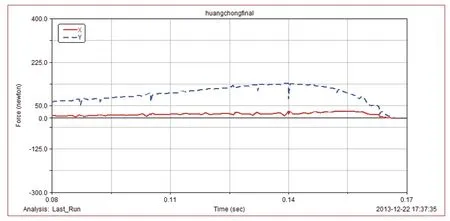
图12 仿真机构起跳时脚部受力情况

图13为仿真机构在仿真全过程中脚部（即E点）的受力情况，在落地瞬间受力约为15kN，可见该方案的又一优势是落地时由于弹簧压缩，对躯体起到了缓冲和减震的作用，防止在落地过程中使躯体受损。

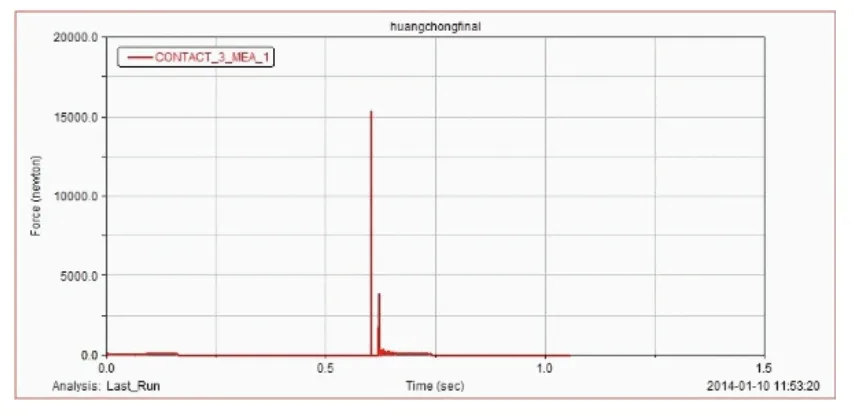
图13 仿真全过程中脚部的受力情况

将机架LAD与水平方向夹角变换为128°时，仿真机构起跳时脚部的受力曲线如图14所示。其中实线为脚部在X方向的受力，虚线为脚部在Y方向的受力，X方向最大蹬地力约为62.6N，Y方向最大蹬地力约为126.3N。

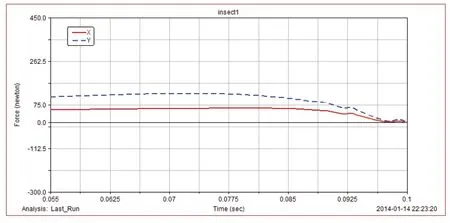
图14 变换机架角度后仿真机构起跳时脚部蹬地力

可见在机架LAD与水平方向夹角减小的过程中，仿真机构脚部在Y方向受力的最大值减小，在X方向受力的最大值增大，因此机架LAD与水平方向夹角不能无限减小，否则当X方向蹬地力远大于脚部与地面间动摩擦力时，会在起跳过程中出现严重的打滑。

2.2.3 电机驱动力分析

弹跳机器人在跳跃前，需通过电机驱动大腿LAB转动，拉动弹簧以储存能量。因此需对转节A进行受力分析。

仿真机构的驱动件即电机的驱动力矩曲线如图15所示，最大驱动力矩为23765.484N·mm。

3 结束语

1）弹跳机器人的弹跳机构采用仿蝗虫腿的四杆机构，能够使小车的跳跃过程平稳可靠、控制简单。在实际应用中，可将机架LAD旋转一定角度来改变起跳曲线的角度，以使小车能够应对不同类型的障碍。在落地过程中弹跳机构能够对车体起到缓冲的作用。

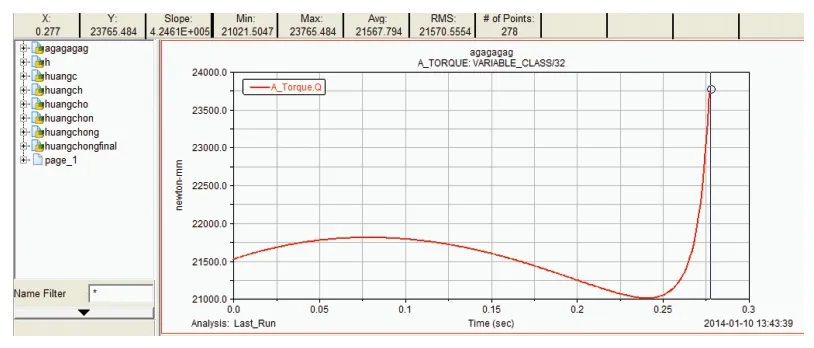
图15 电机对大腿AB的驱动力矩

2）建立了弹跳机器人的弹跳机构的三维模型与虚拟样机模型，并对其进行了基于ADAMS的运动学与动力学分析，验证了弹跳机构采用仿生机构的可行性。

3）通过仿真验证了设计的合理性，弹跳机器人具有良好的弹跳性能，跳跃高度可达约360mm，跳跃距离可达约310mm。变换机架角度后跳跃高度可达约250mm，跳跃距离可达约630mm。

[1]刘壮志,席文明,朱剑英,等.弹跳式机器人研究[J].机器人,2003,25(6):568-573.

[2]郑笑梅.装上发条的间谍[J].国外科技动态,2000,367:35-35.

[3]Hale E,Schara N,Burdick J,et al.A minimally actuated hopping rover for exploration of celestial bodies[A].Robotics and Automation,2000.Proceedings.ICRA’00.IEEE International Conference on.IEEE[C].2000,1:420-427.

[4]Okubo O H,Nakano E,Handa M.Design of a jumping machine using self-energizing spring[A].Intelligent Robots and Systems’96,IROS 96,Proceedings of the 1996 IEEE/RSJ International Conference on.IEEE[C].1996,1:186-191.

[5]张文涛,葛文杰,李建华,等.“袋鼠”跳跃机器人动力系统方案设计与研究[J].机器人,2008,30(4):359-363.

[6]Burrows M,Morris G.The Kinematics and Neural Control of High-speed Kicking Movements in the Locust[J].The Journal of Experimental Biology,2001,204:3471-3481.

[7]陈勇,陈东辉,佟金,等.生物的跳跃形态与仿生跳跃机器人[J].2006.

[8]陈东良,吴磊,王康,等.仿蝗虫弹跳腿机构研究[J].中国机械工程,2011,22(2):166-169.

[9]陈勇,陈东辉,佟金,等.仿蝗虫机器人跳跃机理的实验研究及运动形态的三维动态仿真[J].2006.

[10]王忠,朱洪俊.Tchebycheff Lambada 近似直线导引机构尺度探究[J].机械设计,2007,24(12):27-29.