基于FPGA的大围数QC_LDPC码的译码器

胡 娟，仰枫帆

(南京航空航天大学电子信息工程学院，江苏南京 210016)

LDPC［1］码是近年来发展较快且日趋成熟的一种信道编码方案，因其具有的优越性能和实用价值而被人们认知，但由于随机结构的LDPC码编译码器硬件实现较为复杂，具有的准循环特性QC_LDPC码已成为 IEEE 802.11n(WiFi)、IEEE 802.16e(WiMAX)［2］、(DVB－S2)［3］等众多标准的信道编码方案。LDPC码是一种基于稀疏校验矩阵的线性分组码，具有类似于Turbo码的良好纠错性能。1981年Tanner提出的用二部图表示一个低密度线性分组码的方法，成为LDPC码的主要分析工具［4］。若LDPC码的Tanner图是无环的，那么与积SP(Sum－Product)译码算法可实现最佳译码［5］，若存在环尤其是短环的话，则由和积算法计算所得的概率并非真正的后验概率(这是因为迭代过程中的独立性假设不能成立)，因而译码并不是最优的逐符号最大后验概率译码［6］，因此，环的存在大幅影响了译码的性能。MacKay和Neal经过大量的仿真结果证明信息传递算法(Message－Passing Algorithm，MPA)在Tanner图中有环的情况下仍具有较好的译码性能，但短环的存在还是会降低译码性能。因此通过增大码的最小围数(环长)，可提高码字的性能，围数达到一定的值就可接近无环时的性能。

文献［7］提出一种围数为8的低密度校验矩阵的设计算法，获得的QC_LDPC码在AWGN信道下的仿真结果表明，其具有逼近随机QC_LDPC码的误码率性能。本文采用该算法构造的校验矩阵属于正规的QC_LDPC码，具有更好的分块循环移位特性，大幅降低了编译码复杂度，而Mansour和Shanbhag则提出了一种LDPC 译码策略——分层译码(Layered decoding)［8］，本文采用分层译码方案，为降低硬件复杂度，在Mansour和Shanbhag的基础上进一步优化，采用更为简单的归一化最小和算法(NMS)代替了传统的和积算法(SPA)。整个译码过程只包含比较、移位和加减运算，运算量比SPA算法大幅降低，同时译码性能损失可不超过 0.1 dB［9］。

1 校验矩阵的构造

该方法构造的是一个列重为3，行重＞3的校验矩阵。首先构造3个子矩阵D、E和F，然后将子矩阵D、D和F按照行的方向排列生成H1，H1=［D E F］，再将H1转置生成矩阵H2，最终用p×p的单位矩阵及其移位矩阵作为随机因子，对矩阵H2中的“1”进行随机扩展，即可生成所需的校验矩阵H。

1.1 子矩阵D的构造

构造一个 v行、v2列的矩阵 D0，其中 D0的元素D0(1，1)=D0(2，1)=D0(3，1)= … =D0(v，1)=1，其余元素均为0，

(1)将矩阵D0中的元素向右循环移位，每移动1位生成一个新矩阵。当D0中所有元素为1的列移动到第v2列时移位完毕，共生成v2－1个新矩阵D1，D2，D3，…，Dv2－1。

(2)将 D0，D1，D2，D3，…，Dv2－1按照列的方向排列便生成子矩阵 D=［D0，D1，D2，…，Dv2－1］T，其维数为v3×v2。

1.2 子矩阵E的构造

(1)构造一个v行、v2列的矩阵E0，其中E0中的元素 E0(1，1)=E0(2，2)=E0(3，3)= … =E0(v，v)=1，其余元素均为0，即E0的前v列所构成的块为单位矩阵。如，当v=4时

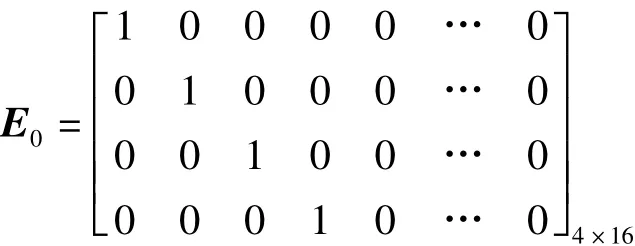
(2)将v个E0矩阵按照列的方向排列生成矩阵E1=［E0，E0，…，E0］T。

(3)将矩阵E1向右循环移位，每移动v位生成一个新矩阵，由此共生成v－1个新矩阵，分别记为E2，E3，…，Ev。

(4)将 E1，E2，E3，…，Ev按照列的方向排列生成子矩阵 E=［E1，E2，E3，…，Ev］T，其维数为 v3× v2。

1.3 子矩阵F的构造

(1)构造一个v行v2、列的矩阵F0。其中F0中的元素 F0(1，1)=F0(2，v+1)=F0(3，2v+1)= … =F0(v，v2－v+1)=1，其余元素均为 0。即在 F0中，从第2行开始，每行中的元素“1”的列位置较上一行中的“1”向右移动v位。假设，当v=4时

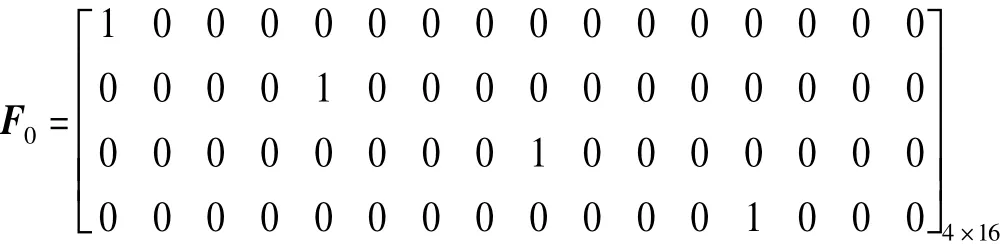
(2)将F0向右循环移位，每移动1位生成v－1个新矩阵，共生成个新矩阵时停止移位，将新矩阵记为F1，F2，F3，…，Fv－1。

(3)将 F0，F1，F2，F3，…，Fv－1按照列的方向排列，生成的矩阵记为 Fv=［F0，F1，F2，F3，…，Fv－1］T。

(4)将v个Fv按照列的方向排列生成矩阵F=［Fv，Fv，…，Fv］T，其维数为 v3× v2。

1.4 矩阵H 2的扩展算法

将生成的子矩阵按行排列得到H1

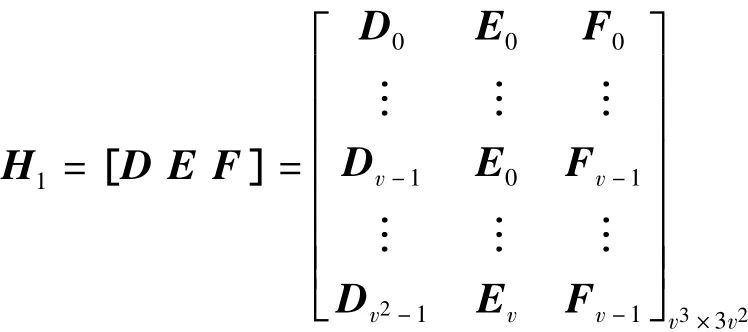
然后再将H1转置，得到矩阵 H2，其中H2的维数为3v2× v3，H2=HT1。

1.5 扩展H 2得到校验矩阵H

(1)设一个单位矩阵I的维数为p×p，则

(2)随机产生1～p之间的随机数，该随机数即为单位矩阵的循环移位数。

(3)将矩阵H2中的“1”用产生的随机数来替代。

(4)将矩阵中的随机数用对应的置换矩阵替代填充，而矩阵H2中的元素“0”用p×p的零矩阵代替，由此即可生成所需的校验矩阵H，其维数为3pv2×pv3。

文献［7］中也给出了4环和6环的检验算法，同时可验证按照此方法得到的校验矩阵最小围长为8。

2 QC_LDPC码的译码算法

置信传播(Belief Propagation，BP)算法是LDPC的标准译码算法，在其基础上又可改进得到最小和(Min－Sum)算法、归一化最小和(Normalization Min－Sum，NMS)算法等。此类算法皆通过校检节点更新和变量节点更新两步完成一次译码迭代，因此又称为2项迭代置信传播(Two Phase Message Passing，TPMP)算法。TPMP算法因为在一次迭代过程中，全部校检节点更新完后，才对所有变量节点进行更新，所以在一次迭代过程中，所有信息只能进行一次更新，收敛速度较慢，译码延时较大。虽此后又提出了复用处理的方法［10］，但未能从根本上提升算法的收敛性和译码性能。

2.1 QC_LDPC码的分层译码策略

分层译码策略则改变了TPMP算法的译码方式，其将校检矩阵按行或列划分成若干分层。在一次迭代过程中，先并行更新第1分层中的所有校检节点和相关的变量节点，然后逐层进行更新。因此在一次更新过程中，后更新的分层会利用已更新分层的输出信息，变量节点在此过程中得到多次更新，大幅加快了译码的收敛速度，并提高了译码性能。但为确保变量节点信息在各分层之间能够进行传递，校检矩阵一个分层中的列权重必须＜1。

2.2 分层迭代译码算法

由上述子矩阵移位法构造的是规则的QC_LDPC码，因而采用分层译码时通常就是将校验矩阵行重的一个子块行作为一个分层，以码长3 456，码率为1/2的(3，6)正规 QC_LDPC码为例，基阵大小为108×216，填充矩阵块为16×16，以每个子块行作为一个分层即每个分层16行，共有108个子层。

设高斯白噪声信道的噪声方差为σ2，接收到的信号序列为y，校验矩阵H的大小为M×N。迭代过程中信道固有信息Zn，校验节点信息Lm，n，变量节点信息Zm，n，其中0≤m≤M －1，0≤n≤N －1。以 BPSK 调制为例，NMSA为基础，将分层迭代译码算法的译码过程列述如下

(1)初始化

(2)迭代过程(第t次迭代的第k层)。

Step1分层更新。

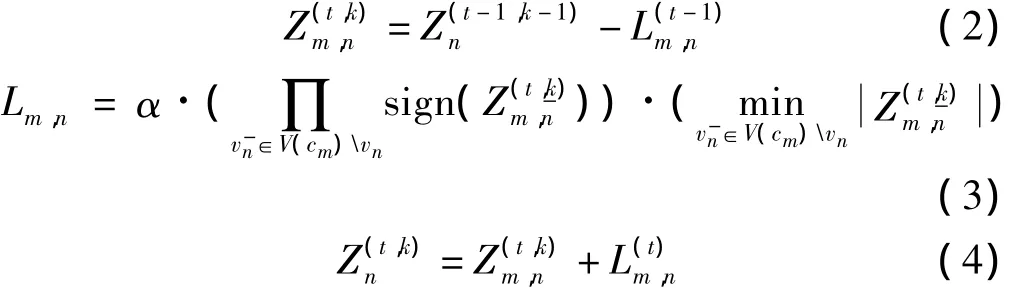
式中，当t=1时，设L(0)m，n=0，m为属于第 k层的校验节点。

Step2译码判决。若 Zj＜0，则=1，否则=0，更新译码结果c^。

(3)译码结构校验。完成一次迭代后，对更新的译码结果进行校验。若满足HT=0，或迭代次数达到系统设置的最大迭代次数，则停止译码，并输出译码结果。否则，跳回步骤(2)进行新一次迭代。

3 正规QC_LDPC码的译码器

3.1 译码器的结构

对码长为3 456，码率为1/2的(3，6)正规QC_LDPC码，子矩阵大小为16×16，共有108个子块行，216个子块列，648个非零子矩阵。采用分层迭代译码算法实现译码器，译码过程中只保存Zn和Lm，n两种中间数据，变量节点信息则通过式(2)计算得出，以减小数据存储量。为便于硬件实现，选择α=0.75作为修正因子，这样只需简单的带符号位右移和加法运算便可完成数据修正。由于将每一个子块行作为一个分层，因此译码器的并行度为108，即共需108个基本运算单元。对译码器中的数据进行6 bit量化，并对计算过程中产生的溢出数据采用截断处理，这样的量化处理使译码性能约有0.1 dB的损失，但节约了硬件资源。

图1为分层译码器的整体硬件结构。

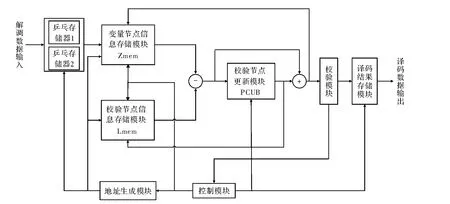
图1 分层译码器的整体硬件结构

(1)数据输入模块。接收解调模块输出量化后的对数似然比数据，完成Zn的初始化。该模块采用乒乓操作，即当其中一个存储器接收数据的同时，译码器从另外一个存储器中读取数据进行译码，以此来提高译码器的吞吐量。

(2)数据存储模块。根据译码过程中所存储数据的不同，存储模块可划分为3块:1)后验概率存储模块Zmem，用于存储Zn。单个Zn的长度为6位，每个子块列对应的存储空间为6×16=96位，对应子块列数，共需216个此类模块。2)校验信息更新存储模块Lmem，用于存储，单个的长度为6位，每一行有6个非零元素，所以每行对应的存储空间为6×6=36位，而每一子块行所对应的存储空间为6×6×16=576位。对应子块行数，共需108个此类存储模块。3)译码结果存储模块，用于存储译码的结果。每一子块列对应的译码数据长度为16位，对应子块列数，共需216个此类存储空间。同样为了提高吞吐量，译码数据输出模块也采用乒乓操作，当一个存储器进行译码结果更新时，另一个存储器向外设输出存储器中的译码结果。

(3)校验节点更新模块(Parity－Check Update Block，PCUB)。校验节点模块是译码器的核心处理单元，完成迭代的更新过程。共有108个PCUB模块进行并行处理，一次更新108组数据。每一组相关的6个变量节点信息串行输入PCUB中的FIFO寄存器，并逐次进行比较，寻找该组数据中的最小值与次最小值。当一组数据输入完成后，最小值与次最小值得以确定，再从FIFO寄存器中依次读出数据同最小值与次最小值比较，再更新数据。迭代译码过程主要被划分成两个阶段，变量节点信息输入FIFO阶段和变量节点信息输出FIFO阶段。这样的结构适合采用二级流水线，当一组已输入的变量节点信息从FIFO中读取时，将下一组变量节点信息输入FIFO。通过二级流水线处理，提高了近一倍的数据吞吐率。

(4)地址生成模块。地址生成模块中包含一个保存校验矩阵中所有子块位置和子块偏移量信息的只读寄存器(ROM)。通过从ROM中调取信息，分别产生Zmem和Lmem的读写地址。

(5)校验模块。校验模块在每一次迭代结束之后，对所有校验方程进行验证，若全部满足则停止迭代，否则进行下一次迭代过程，直至达到预先设定的最高迭代次数为止。

(6)控制模块。控制模块中设置整个译码器的状态机，控制译码器各个子模块有序运行。

3.2 译码器中内存读取的问题及改进

在PCUB模块中，每个校验节点对应的6个变量节点信息串行加入迭代过程，而这些节点信息存储在与之对应的216个Zmem中。由于校验矩阵列重为3，因此，若按照校验矩阵原来的结构，当108个PCUB并行从Zmem中读取数据时，顺序读取变量节点信息时可能从某一子块列对应的Zmem中读取1～3个数据，这样不同的读取情况，会增加Zmem的硬件设计复杂度。

由于变量节点信息加入迭代过程的先后顺序并不影响译码器的结构，因此对变量节点信息的读取顺序加以改进，将原有的读取顺序重新排列，使得在同一时刻的PCUB从不同的子块列对应的Zmem中读取数据，即每一时刻Zmem最多提供一个数据，这便大幅降低了Zmem的设计复杂度，进而提高硬件的通用性。

4 FPGA实现

选用Altera公司StratixIII系列的EP3SL340器件，设置最大迭代次数为5次，在QuartusII 9.0下完成综合与布局布线，硬件资源消耗如表1所示。

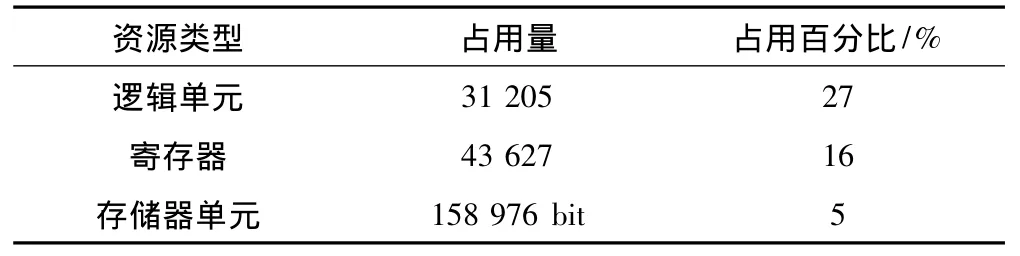
表1 译码器硬件资源消耗统计

在译码过程中，首先花费108个时钟进行Zmem的初始化过程，完成后开始迭代译码。在每一次迭代过程中，PCUB模块进行108次更新，由于采用流水线结构，每次更新实际仅需花费6个时钟，再加上第一组数据进入流水线花费的额外6个时钟，5次迭代共花费6×(108×5)+6=3 246个时钟。

图2为传统迭代与分层迭代译码算法的性能曲线比较，为AWGN信道模式下采用BPSK调制，进行6 bit量化。通过图中的性能曲线可看出，在最大迭代次数同为5次的情况下，对正规QC_LDPC码采用分层译码器处理后相比采用传统部分并行结构译码器具有较好的译码性能表现，在信噪比为2.5 dB的情况一，误码率可以达到10－5量级。

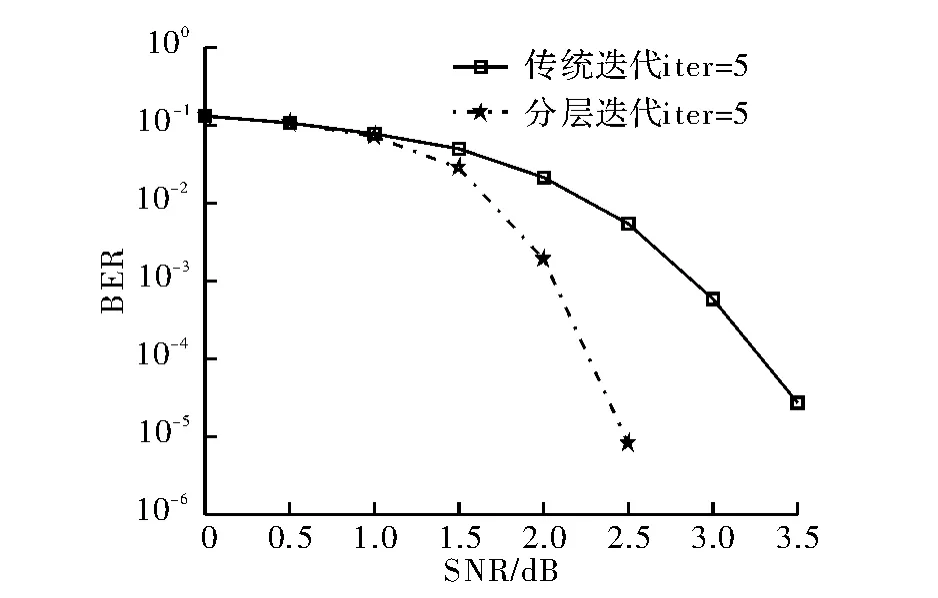
图2 传统迭代与分层迭代译码算法的性能曲线比较

5 结束语

文中首先利用3个不同的子矩阵分别按照指定的方法进行移位运算，组合得到无4环和6环的基阵，进而利用单位矩阵及其移位矩阵作为替换因子随机替换基阵中的“1”而扩展得到所需的校验矩阵。随后采用分层译码算法，该算法较传统的部分并行结构有较好的收敛性，并降低了迭代次数的要求。同时在Altera公司的StratixIII系列FPGA上得以实现，验证其达到了较高的译码吞吐量。

［1］GALLAGER R G.Low －density parity－check codes［J］.IRE Transaction on Information Theory，1962，IT － 8(1):21－28.

［2］IEEE.LDPC coding for OFDMA PHY.802.16REVe sponsor ballot recirculation comment［S］.USA:IEEE，2004.

［3］DE －DIN.Digital video broadcasting(DVB)，second generation:ET － SI EN 302 307 v.1.1，［S］.USA:DE －DIN，2005.

［4］MACKAY D J C，NEAL R M.Near shannon limit performance of low density parity check codes.［J］.Electronics Letters，1997，33(6):457 －458.

［5］WIBERG N.Codes and decoding on general graphs［D］.Linkoping，Sweden:Linkoping University，1996.

［6］MACKAY D JC.Good error－ correcting codes based on very sparse matrices［J］.IEEE Transaction on Information Theory，1999，45(2):399 －431.

［7］范俊，肖扬.基于子矩阵移位法的大围数LDPC码设计［J］.铁道学报，2007，29(6):57 －62.

［8］MANSOUR M M，SHANBHAG N R.High－throughput LDPC decoders［J］.IEEE Transaction on Very Large Scale Integration Systems，2003(11):976 －978.

［9］张桂华，张善旭，李颖.高吞吐量低存储量的LDPC码译码器FPGA实现［J］.西安电子科技大学学报:自然科学版，2008，35(3):427 －432.

［10］SHIH Xinyu，ZHAN Chengzhou，LIN Chenghung，et al.An 8.29 mm2 52 mW multi－mode LDPC decoder design for mobile WiMax system in 0.13 μm CMOS process［J］.IEEE Journal of Solid － state Circuits，2008，43(3):672－683.