多重滤子非单调新锥模型信赖域算法

周新慧，李小伟

(西安电子科技大学理学院，陕西西安 710071)

考虑无约束优化问题

其中，f(x)∶Rn→R1是二次连续可微函数，对于求解式(1)目前主要有线性搜索和信赖域两类数值方法，信赖域因为其强收敛性、强适性和稳定性等优点，受到最优化研究者的高度重视。目前众多学者对其进行了深入研究，传统的信赖域算法具有单调性，使得步长的选择具有一定的局限性，因此Deng等人，将1986年Grippo及Lucidi提出的求解无约束问题的非单调线性搜索方法［1］中的非单调技术引入到信赖域算法当中，构造了无约束优化信赖域算法，相应的数值试验表明，该算法的有效性。2004年 Zhang和Hger［2］提出了新的非单调技术。但Gu和Mo发现每次更新ηk和Qk使得算法的变得更为复杂。因此在此基础上Gu和Mo［3］提出了另外一种非单调技术。1980年，Davidon针对二次模型对于非二次性太强、曲率变化较为剧烈的函数，逼近效果差等缺陷提出了锥模型［4］。之后倪勤等提出了新锥模型的子问题，取消了对信赖域半径和水平向量的限制，将新锥模型［5］与新的可行集分成3种情形，由此得到3种不同类型的锥模型信赖域子问题。

过滤技术是由Fletchh和Leyffer于2002年在开创性工作中提出的解非线性规划的一个新的总体化技术，目前过滤技术已得到广泛的应用并取得了较好结果，而学者将多重过滤技术运用于二次模型［6］及新锥模型［7］中的信赖域算法中也取得了良好的效果。

在上述基础之上，本文提出了基于新锥模型的非单调信赖域过滤算法

1 算法

本文将Gu和Mo提出的非单调技术应用到新锥模型信赖域算法中定义一种新的比率，考虑到锥模型求解量大，又将过滤技术加入其中，从而减少新锥模型的运算次数。提出新锥模型的非单调多重滤子信赖域算法。

1.1 新锥模型的子问题

新锥模型信赖域的子问题［2］

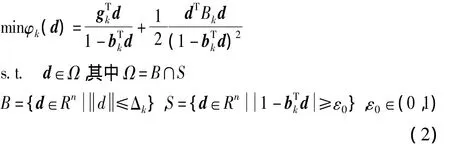
1.2 非单调技术

Gu和Mo［3］提出了一种新的非单调技术

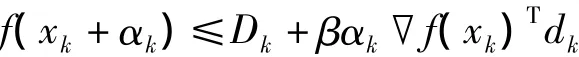
其中

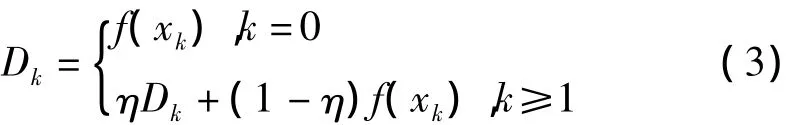
η∈(0，1)。运用非单调技术将比值γk的制转换为(4)

1.3 过滤技术

定义 1［8，10］令 F=(g，…，g)T，其中 g=k，1k，nk∈lk，lgl(xk)是点xk处的梯度向量的第i个分量，I是一个指标集。若任取 k，l∈I，都有对至少一个i∈(1，…，n)成立，称F是由n维梯度向量组成的过滤集。

1.4 多重滤子非单调的新锥模型信赖域算法

Step1计算gk，若则停止，否则转Step2。

Step2用折线法求出该子问题的近似解dk。

Step3计算γk。

Step4确定实验步骤的可接受行。

(1)若 γk≥ρ，则接受 sk令 xk+1=xk+sk转 Step5，否则转(2)。

(2)令 j=0，βk，j=1。

(3)若 j＞M，则令 xk，j=xk转 Step5;否则转(4)。

(4)令 xk，j=xk+ βk，jsk若点 xk，t被当前过滤集 F 接受，则转(5)。否则令 βk，j= αβk，j，t=t+1 转(3)。

(5)令 βk= βk，j，xk+1=xk+ βkdk。

Step5更新信赖域半径。

若 γk≤ u，则令4Δk};若 γk≤u，令 p=p+1

Step6k=k+1，更新 bk，Bk，若 ρk≥u 转 Step1。

2 收敛性的证明

假设:

H1序列{Bk}，{bk}一致有界，即存在M＞0，对

H2水平集有界且f(x)在水平集上二次连续可微且有下界。

H3g(x)在水平集上是Lipschitz连续的。

H4

引理1［9］算法产生的点列xk满足

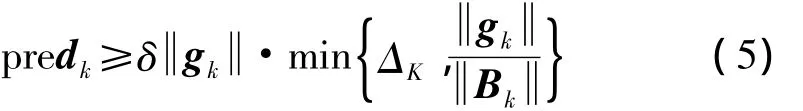
引理2［10］若假设成立算法产生的点列xk对于任意的k都满足数列fk+1≤Dk+1≤Dk且数列Ck收敛。证明见文献［10］引理3。

引理3［3］假设H1～H4成立，且存在常数 δ＞0，使，对于任意的k存在m＞0，有

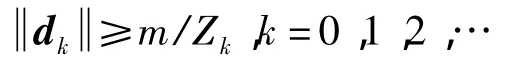
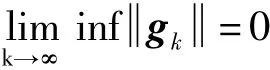
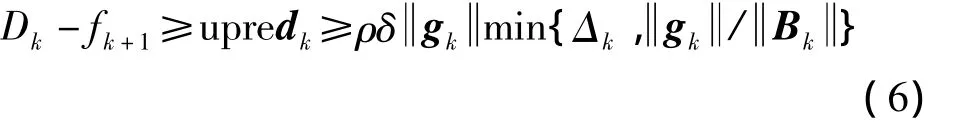
以下反证法证明定理的成立。假设存在充分大的k2＞k1，当 k≥k2时，存在常数 δ＞0，使 gk≥δ，∀k根据式(6)可得

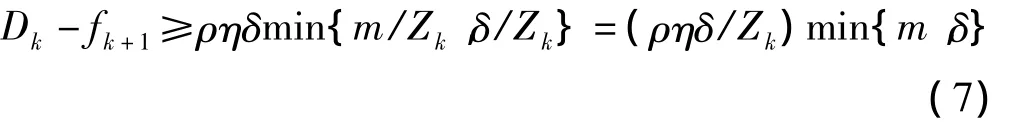
令 λ =(ρηδ)min{m，δ}，则(7)式可变为

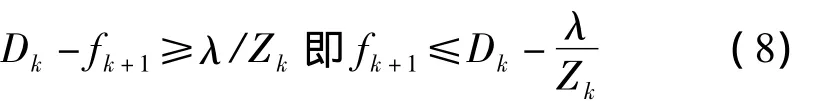
由Dk得定义和式(8)可知

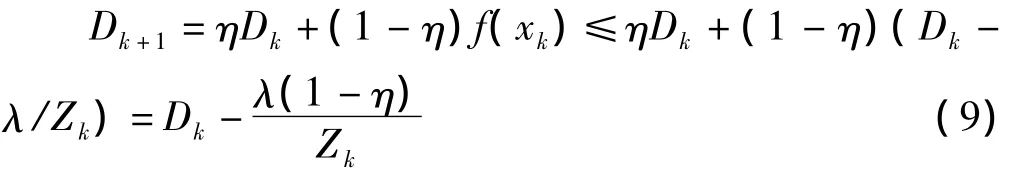
结合式(9)可得由式(10)整理可得

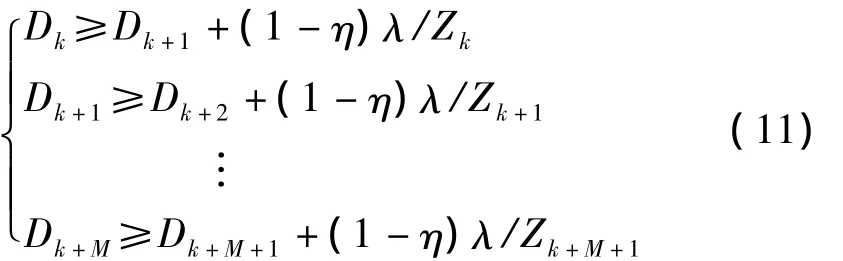
在上式两边取最大值，有

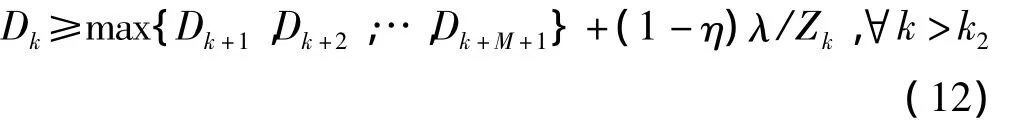
根据引理2 可知 Dk+M+1≤max{Dk+1，Dk+2，…，Dk+M+1}，∀k，从而有

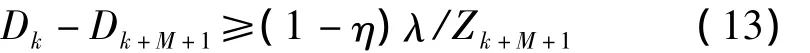
对上式及序列{Zk，k=0，1，2，…}单调上升，可得

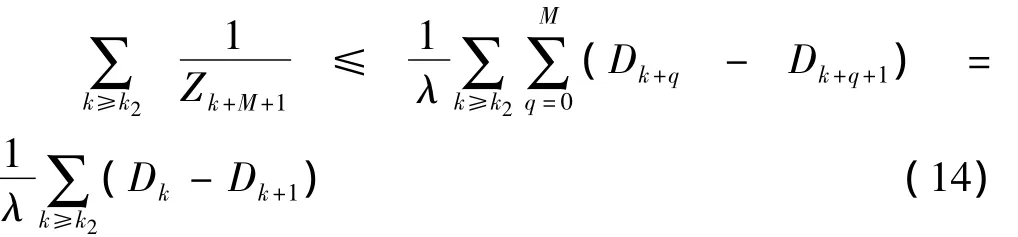
由式(14)两边取极限及引理4可得

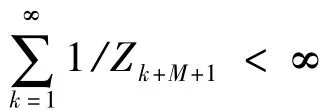
这与假设H2矛盾。

3 数值试验

为说明算法的有效性，用Matlab编写程序对本文算法进行数值测试，其中Nf，Ng分别表示函数值和梯度值的迭代次数;n表示问题的维数。参数选择如下:ρ=0.1，Δ0=1.0，u=0.75，ε0=0.01，B0=I，ε =10－6。测试函数1 Extended Rosenbrock funtion:f(x)=。测试结果如表1所示。

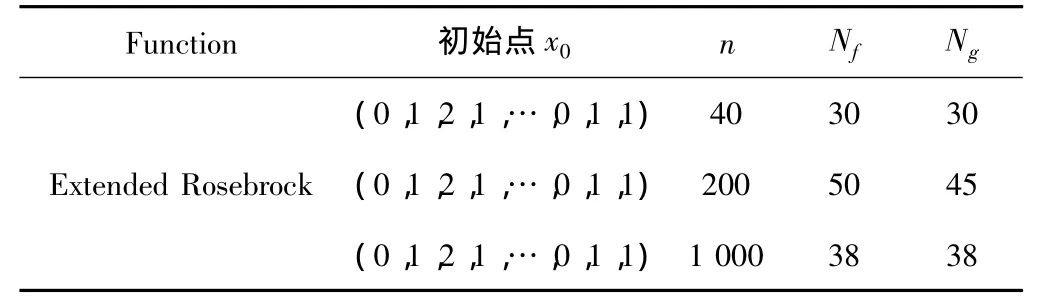
表1 测试结果

由测试结果可以看出本文所提出算法的的有效性和可行性

4 结束语

本文在求解无约束优化问题的新锥模型信赖域算法中加入了非单调技术和多重过滤技术，目的是减少运算次数及加大试验点被接受的几率，数值试验表明，新算法对解决问题的有效性及可行性，并在一定条件下证明了算法的全局收敛性。

［1］GRIPPO L，LAMPARIELLO F，LUCIDI S.A nonmonotone line search technique for Newton's method ［J］.SIAM Journal on Numer.Anal，1986，23(4):707 －716.

［2］ZHANG H C，HAGER WW.A nenmonotone line search technique and its application to unconstrained oiptimization［J］.SIAM Journal on Optimization，2004，14(4):1043 －1056.

［3］GU N Z，MO J T.Incorporating nonmonotone strategies into the trust region method for unconstrained optimization ［J］.Applly Mathmatic Computer，2008(55):2158 －2172.

［4］DAVIDON W C.Conic approximation and collinear scaling for optimizers［J］.SIAM Journal on Number.Anal，1980，17(2):268－281.

［5］NI Q.Optimality conditions for trust－ region subproblems involving a conic model［J］.SIAM Journal on Optimization，2005，15(3):826 －837.

［6］GOULD N I M，PH L，TOINT C S.A filter－ trust－ region method for unconstrained optimization［J］.SIAM Journal on Optimization，2006，16(2):341 －357.

［7］MIAO Weihua，SUN Wenyun.A filter trust－ region mothod for unconstrained optimization［J］.SIAM Journal on Optimization，2007，17(8):561 －568.

［8］缪卫华，孙文瑜.一个解无约束优化问题的过滤依赖域方法［J］.高等学校计算数学学报，2007，29(1):88 －96.

［9］王庆.新锥模型信赖域算法［D］.太原:太原科技大学，2009.

［10］赵绚.新锥模型信赖域算法［D］.太原:太原科技大学，2010.