基于ANSYS的起重机新型弧弦主梁力学分析
2014-12-18李新华陈泽宇
李新华,陈泽宇,刘 洋
(中南林业科技大学 机电工程学院,长沙 410004)
0 引言
门式起重机是一种搬运大型物料的起重设备,广泛用于国民经济的各个部门,在现代化生产中占有重要地位[1]。随着门式起重机的使用范围越来越广,对其安全性能和力学性能也越来越重视。目前市场上的门式起重机中主梁大多采用平直主梁结构,很少采用其他新型主梁结构形式。下承式拱桥随处可见,因为这种梁-拱组合体系同时具备受弯和承压的特点而广泛应用。其结构的主要优点是利用梁的受拉,来抵消拱在竖向载荷下产生的水平推力[2]。本文依据下承式拱桥的受力特点,参照该桥梁的结构形式,提出了一种新型弧弦主梁结构,并利用ANSYS对改进后的主梁进行力学分析。
1 新型弧弦主梁的结构模型
新型弧弦主梁(以下简称新型主梁)的结构设计,就是在原来传统主梁的基础上,加设一弧形梁,中间通过焊接连杆与平直梁连接,新型主梁结构如图1所示。

图1 新型主梁结构
理论上,这种新型主梁可以利用平直梁的受拉来抵消弧在小车竖向载荷作用下产生的水平力,与传统主梁相比,减小了在竖向载荷的作用下产生的最大应力和应变[3]。图2分别为传统主梁和新型主梁的受力简图,根据图2来比较两种主梁的弯矩及挠度。
1)传统主梁的弯矩和挠度:
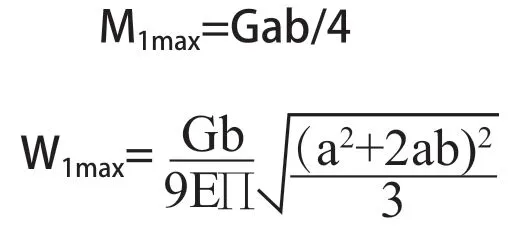
2)新型主梁的弯矩和挠度:
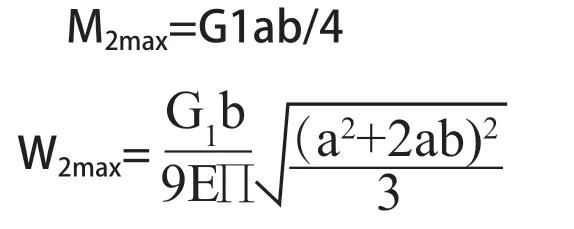

图2 受力简图
由于新型主梁在竖直方向的力被弧梁和拉杆分担了一部分,则G1=G-G2,其中G为吊重。根据图1所示,F1=G2Sina;F2=G2Cosa,弧梁和连杆将一部分的竖向力分解成了切向力和径向力,明显可得M1max>M2max;W1max>W2max。新型主梁的弯矩和挠度都小于传统平直梁的弯矩和挠度。理论上证明了在相同的载荷作用下,新型主梁结构上产生的最大应力和应变要小于改进前传统主梁。
2 有限元建模
2.1 主要参数
该门式起重机的跨度为22.5m,额定起升量Pg=30t,小车的轮距3.6m,两相邻大隔板的间距1.5m,隔板厚度0.006m。腹板的高度H=1.3m,两腹板的间距B=0.5m,腹板的厚度t3=0.006m,上下盖板的厚度t1=t2=0.016m,主梁的截面图如图3所示。
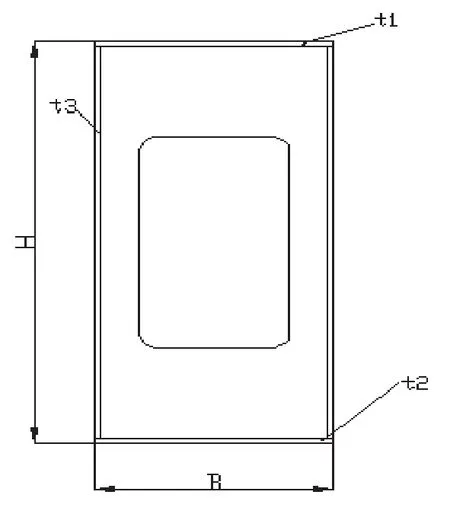
图3 主梁截面
2.2 模型建立与网格划分
在ANSYS前处理模块中分别设置分析类型、单元种类、实常数以及材料参数。在本文中主要采用SHELL63单元和BEAM188单元。SHELL63具有弯曲和薄膜能力,且该平直梁板材的长度不小于其厚度的10倍,应选用SHELL63单元[4]。弧形梁和起连接用作的连杆采用BEAM188单元,该单元适用于应力强化部分,符合弧形梁和接连杆的实际受载情况。建模过程中采用自下而上的方法,通过依次创建关键点、线、面等单元达到最终的建模效果。新型梁的材料都采用Q345,其具体参数如表1所示。

表1 材料参数
网格划分是ANSYS有限元分析的重要环节,网格划分的方法和类型直接影响单元的规模和分析的计算精度[5]。网格划分太稀,计算简便,但是计算精度不高,与实际工作情况相差较大。网格划分太密,会提高分析结果的计算精度,但同时会使单元规模和计算规模增大,增加计算机的计算负担,因此要综合考虑计算规模和计算精度来确定网格大小[6]。本例中,通过多次的计算分析,确定网格大小为0.1m,采用自由划分产生的节点个数为8494,网格划分后的有限元模型如图4所示。

图4 主梁网格模型
2.3 边界条件的设置和危险工况选择
实际情况中,该主梁与端梁是搭接相连的,所以把主梁左右两端的面上都加上全约束,这样能比较真实地模拟出主梁与端梁的连接。
根据理论力学和门式起重机工作的实际情况,能够确定小车满载制动,置于跨中时,主梁的应变和所受应力值最大,此状态为门式起重机的最危险工况,应该着重分析。为了使起重机正常、安全地工作,起重机主梁结构应该满足强度和刚度的要求。对此类门式起重机应按强度计算载荷-第二类载荷,即起重机按工作状态最大载荷进行强度计算,应选取可能出现对主梁最不利的载荷组合[7]。
2.4 载荷施加
该门式起重机的计算参数:小车自重Pc=8564kg;额定起升重量Pg=30t;动载荷系数φ=1.25;内陆风压q=150N/m2。工作中,小车运行在轨道上,而轨道铺在主梁的上盖板。为了分析简便,可以认为载荷是直接施加在主梁的上盖板面上,选择车轮附近上盖板面上的节点为受力点,把最大轮压平均加载在所选的节点上[8],每个车轮的载荷大小为F=G总/4=120512.5N。
3 静力学分析
静力学分析主要是指计算分析结构的应变、应力的分布和大小,用最大的符合应力评价结构的静强度、最大的符合应变评价其静刚度[9]。主梁结构主要采用Q345钢,其屈服极限φ=345MPa,安全系数取n=1.34,主梁的许用应力为 [σ]=σa/1.34=257.5MPa,起重机的许用挠度为[f]=L/800=28mm。
分别对两种不同起重机主梁在同一危险工况下进行有限元分析,得到的有限元分析结果(如图5、图6所示),获得了起重机主梁在相同工况下改进前后的最大应力和应变的值以及分布情况。
从应力云图可以直观看出新型主梁的应力分布比传统主梁的应力分布更均匀,新型主梁上的弧梁和连杆也相应的承担了一部分力,在连杆与主梁的连接处、连杆与弧梁的连接处,应力大小为31MPa左右。整个新型主梁结构的应力呈对称分布,在车轮点处出现应力集中,最大应力为171MPa,这是受到集中力的原因。另外在主梁与端梁的搭接处也出现了应力集中,应力大小为99.4MPa,可能是对主梁结构单独建模时,仅简单的在此连接面施加了全约束所致,主梁上其他部分的应力为19MPa。从应变云图看出,新型主梁的跨中处变形大的范围减小了,结构的变形也是对称分布,趋势是由中间向两端逐渐变小。

图5 传统主梁的应力和应变云图
从分析结果来看,结构改进前的最大应力是为188MPa、最大应变为9.2mm,改进后的最大应力为171MPa、最大应变为6.6mm,均小于许用的应力和应变,满足设计的要求。结构改进后的应力、应变的改善量分别为9.04%和26.26%。

图6 新型主梁的应力和应变云图
4 结论
通过对起重机主梁结构改进前后的静力分析结果的对比,发现新型主梁结构的应力、应变较结构改进之前的应力、应变有所减小。进一步证明了这种新型弧弦主梁结构形式不仅改善了应力、应变的大小和分布状况,并且有很大的设计余量,在符合设计的前提下,可以对主梁的尺寸优化,达到节约钢材、降低制造成本的目的,更为起重机的轻量化发展和主梁的新式结构设计提供了参考。
[1]王金诺,于兰峰.起重运输机械金属结构[M].北京:中国铁道出版社,2002.
[2]姜晨光.桥梁建造技术指南[M].北京:化学工业出版社,2011.
[3]蒋连海,李新华.弧弦梁的研究及其在起重机主梁上的应用[J].制造业自动化,2014,36(7):76-77,129.
[4]贾振杰,宋晓娟,许映秋,等.基于ANSYS的造船用龙门起重机主梁静力分析[J].机械制造与自动化,2012,41(5):98-100,109.
[5]齐玉红.基于ANSYS的桥式起重机主梁结构优化设计研究[D].郑州大学,2011.
[6]徐锡锋,程文明,蔡锟.参照斜拉桥特点的门式起重机结构改进及有限元分析[J].起重运输机械,2013,(2):65-68.
[7]戚其松,范小宁,徐格宁,等.基于Ansys的门式起重机主梁优化设计[J].起重运输机械,2013,(8):32-35.
[8]秦东晨,齐玉红.基于ANSYS的30t桥式起重机主梁结构优化设计[J].矿山机械,2011,39(5):46-49.
[9]姚志林.10t门式起重机结构强度研究[J].建设机械技术与管理,2006,19(7):96-100.
