基于流固耦合的高精度声速剖面仪支撑结构的结构强度及应力分析

舒竞翔，王收军，李志伟，张宝峰

（天津理工大学 复杂系统控制理论及应用重点实验室，天津 300384）

0 引言

声速剖面仪是一种测量声波在水中传播速度的精密水声仪器，同时通过温度及压力传感器测量温度和垂直深度，能够快速、有效地为测深仪等声呐设备校正测量误差，提供实时声速剖面数据[1]但在声速剖面仪自身标定校验时，需要设计出更高精度的声速剖面仪与其他声速剖面仪进行比对校验，这就需要对高精度声速剖面仪样机机械结构提出更高的设计要求。支撑结构作为仪器整体机械结构的核心部件，其上安装着一对相对的换能器，支架的受力变形将直接导致样机测量数据精度的改变，所以对仪器支架结构进行力学分析尤为重要。对其强度和刚度分析具有十分重要的意义。而样机是在海水搅拌的环境下工作的，所以仪器支架承受的是流体不均匀力的作用，所以采用流固耦合的方法进行分析。因此本文利用ANSYS Workbench平台，对声速剖面仪支撑结构进行单向流固耦合分析，计算出仪器支撑结构在海水搅拌中应力和变形量分布，为仪器的设计提供依据。

1 流固耦合分析方法

流固耦合是研究可变性固体在流场作用下的各种行为以及固体变形对流场影响这二者相互作用的一门科学。ANSYS很早就开始进行流固耦合的研究应用，目前算法和功能已相当成熟，本文采用ANSYS Mechanical APDL+FLUENT进行流固耦合分析。从数据传递角度出发，流固耦合分析分为单向流固耦合分析和双向流固耦合分析。由于支架及搅拌设备的尺寸变形量相对于搅拌槽整体尺寸较小，即其结构变化对流场影响较小，所以采用单向流固耦合进行分析。

但是要对支架进行耦合分析前，需要先完场旋转流场的计算，即一共进行两个耦合计算，先进行搅拌器与流体的计算，得出带有搅拌预应力的旋转流场，然后将得出的流场域与支架结构进行另一个流固耦合计算，从而完成对支架的耦合分析。

1.1 流体控制方程

流体流动遵循物理守恒定律，基本的守恒定律包括质量守恒定律、动量守恒定律、能量守恒定律。

质量守恒方程[2]：

动量守恒方程：

其中，t/s表示时间，ff表示体积力矢量。 fρ/（Kg/m3）表示流体密度，v表示流体速度矢量，fτ/（m/s）表示剪切力长量，可表示为：

其中，p/Mpa表示流体压力，μ/(N·s/m2)表示动力粘度，e表示速度应力张量

1.2 固体控制方程

固体部分的守恒方程可以由牛顿第二定律导出：

其中，sρ/（Kg/m3）表示固体密度，sσ 表示柯西应力张量， fs/ N表示体积力矢量，表示固体域当地加速度矢量。

1.3 流固耦合方程

同样，流固耦合遵循最基本的守恒定律，在耦合交界面处，应满足流体与固体应力（ fτ ）、位移（d）、热流量（q）、温度（T）等变量的相等或守恒，既满足如下四个方程：

2 流固耦合数值计算

利用ANSYS Workbench进行流固耦合计算分析时，首先通过FLUENT软件进行流场分析求得样机支架上的压力分布载荷，然后将求得的载荷导入Static Structural模块中进行结构应力求解分析。

2.1 几何模型建立

首先在SolidWorks中建立支架及搅拌器的几何模型，然后导入到Workbench中FLUENT的前处理模块Design Modeler中，再进行流场的建模。如图1所示，搅拌叶片周围的圆柱形区域空间为搅拌器流场域水体旋转区，在这里将进行搅拌器叶片与静止水体之间的流固耦合。其余三部分为搅拌槽流场域水体静止区，其中中间部分为耦合区流场域水体静止区，内部是样机支架，在这里将进行流场域水体与样机支架机械结构的流固耦合。

在网格划分模块Mesh中进行网格划分，为了确保求解的精确性，对流场进行多域法网格划分，耦合区域水体网格尺寸为10mm，下静止区域水体网格划分为面网格划分，控制网格为10mm，上静止区域水体网格划分为四面体网格，采用默认值。划分得到网格节点数为40798，单元数量为201771。流场网格模型如图2所示。

图1 支撑及搅拌和流场模型

图2 流场域网格划分

2.2 湍流模型选择

选取流场模型时，选择κ -ε 湍流模型。κ -ε型分为标准（standard）、RNGκ -ε 和带旋流修正κ -ε 湍流模型。带旋流修正的κ -ε 模型的优点是对于平板和圆柱射流的发散比率的更精确的预测。κ -ε 模型对于旋转流动、强逆压梯度的边界层流动、流动分离和二次流有很好的表现。带旋流修正的κ -ε 模型和RNGκ -ε 模型都显现出比标准κ -ε 模型在强流线弯曲、漩涡和旋转有更好的表现。所以针对这种特性选取带旋流修正κ -ε（realizable）湍流模型。其方程[3]关系如下：

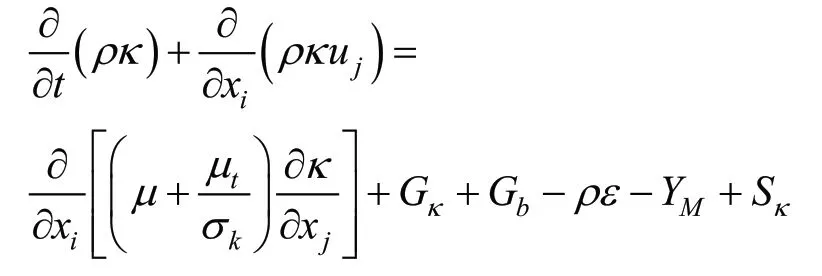
并拥有如下关系：

在方程中κ是湍流动能；ε为耗散率；Gκ是由层流速度梯度产生的湍流动能；bG 是由浮力而产生湍流动能；YM是可压缩湍流中的扩散产生的波动值；1Cε、3Cε为经验常数；R为修正项； κ∂ 和ε∂为湍流动能和耗散率的湍流Prandtl数的倒数。相关常数如下：1Cε=1.42，C3ε=1.68。

2.3 流场参数及边界条件

在实际的操作中流场内注入的是海水，根据海水的参数定义设置为海水的密度取1.025×103kg/m3，平均盐度3.5%。定义搅拌器流场区水域旋转区转速为15rad/s叶轮的转速为15rad/s，轴转速同为15rad/s其余为静止区，动静区域之间设置为交互面（interface a），三个搅拌槽流场域水体，上部和中部两个相邻静止区之间建立交互面（interface b）中部和下部两相邻静止区之间建立交互面（interface c）。

2.4 流场求解

在流场求解方（Solution Methods）法选择基本模式（SIMPLE），算法控制及监视器选择系统默认。

进行求解初始化，选择computer from all zones，进行流场初始化，最后设置迭代次数，选择1500次，完成求解。计算在1226次完成收敛（！1226 solution is converged），如图3所示。

图3 计算收敛曲线

得到流场的流速和应力云图，如图4和图5所示，并得到支撑处的受力，约为3.25N。

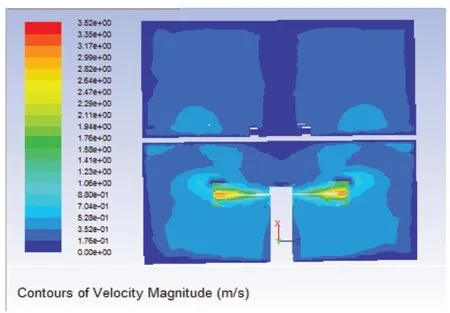
图4 流场速率图

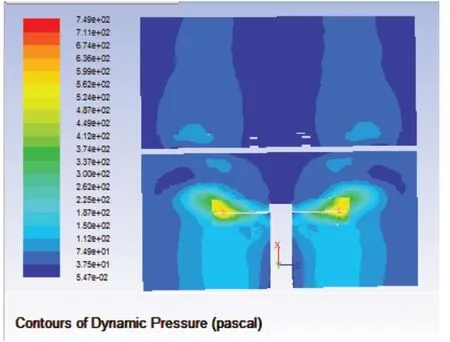
图5 流场应力图

2.5 流固耦合分析

对仪器支撑进行分析之前，需要材料参数的设置。材料选择殷钢(Invar Steel的音译)，属于铁镍合金的一种，其成分为镍36%，铁63.8%，碳0.2%。这种材料最大的特点就是随温度的变形极小，适合于制作对温度变形有严格要求的零件。满足仪器支撑需在海水中尽可能不受到温度的影响，从而保证了对声速测量的准确性。其密度ρ=7900kg/m3，弹性模量E=214GPa，泊松比ν=0.3。

进行仪器支撑的网格划分，为了准确的得到流场分析中耦合面的节点压力值，网格划分尺寸与流场网格划分尺寸一致，控制网格为10mm，划分得到网格单元数为10540，节点数为19857。网格划分结果如图6所示。

图6 仪器支撑网格划分

对支撑施加载荷，在支架外圆周施加固定约束，在支架外表面耦合区施加来自FLUENT对流体计算完成的载荷，如图7所示。从图中可以得出安装换能器位置的两个孔受力为4.47×10-4MP，整个支架受到的最大应力为6.5×10-4MP，受到最小应力为1.9×103MP。

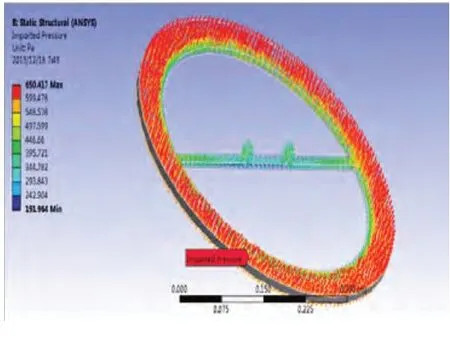
图7 仪器支撑加载应力分布图

加载完成后进行求解运算，得到总体应力云图，如图8所示；总体位移云图，如图9所示。

从图8中可知仪器支撑两边部分承受的应力较大，中间部分也承受了较大应力，最大应力出现在支架横梁与圆盘连接处，大小为0.1MP。

从图9中可知仪器支撑的最大位移出现在支架中间部分，即安装两换能器之间的距离，其形变量为7.8×10-7m。

3 结论

本文通过运用流固耦合分析方法，进行了声速剖面仪支撑结构在海水搅拌预应力下的结构应力分析，完成两个流固耦合的数值模拟分析。

剖面仪支撑结构受旋转海水预应力作用发生变形出现在支架结构中部，即两个换能器之间区域。而最大应力出现在横梁连接处，大小为0.1MP，满足强度要求，证明设计安全可靠性。

两换能器之间最大位移为7.8×10-7m，即7.8nm，产生变形较小，对换能器精度影响小，保证了高精度性，证明了设计的合理性。

[1]关致和,赵先龙,王莉娜.声速仪标定系统[J].气象水文海洋仪器,2004:38-42.

[2]关致和,赵先龙,王莉娜.HY1200系列声速剖面仪[J].气象水文海洋仪器,2004,02:53-57.

[3]李德军,王润田,卜安安.基于高精度时间测量技术的声速仪设计[J].国外电子元器件,2006,06:20-22.

[4]袁启铭.轴流泵叶片流固耦合震动特性分析[D].扬州大学,2009:23-25.

[5]祝克强,吴汉川,乔春.采用流固耦合的混砂车搅拌叶轮应力分析[J].现代制造工程,2012,03:51-54.

[6]唐学林,贾玉霞,王福军.基于修正的RNGκ-ε模型的水翼空化数值模拟[J].工程热物理学报,2012,09:1514-1518.

[7]Numerical Solution Of Fluid-Structure Interaction In Liquid-Filled Pipes By Method Of Characteristics[J].Chinese Journal of Mechanical Engineering,2007,03:44-49.

[8]施卫东,徐燕,张启华.基于流固耦合的多级潜水泵叶轮结构强度分析[J].农业机械学报,2013,05:70-73+100.

[9]Numerical Investigation on Fluid Structure InteractionConsidering Rotor Deformation for a Centrifugal Pump[J].Chinese Journal of Mechanical Engineering,2011,04:539-545.

[10]解元玉.基于ANSYS Workbench的流固耦合计算研究及工程应用[D].太原理工大学,2011:33-35.

[11]娄涛.基于ANSYS的流固耦合问题数值模拟[D].兰州大学,2008:14-18.