切削加工表面粗糙度的预测模型与参数优化

2014-12-18韩兴国祖晓琳

制造业自动化 2014年20期

韩兴国，祖晓琳

（内蒙古科技大学经济与管理学院，包头 014010）

0 引言

切削加工表面粗糙度主要取决于切削残留面积的高度，切削速度，背吃刀量等[1]。而影响切削残留面积高度的因素主要包括：刀尖圆弧半径，主偏角，副偏角及进给量等[2]。而刀尖圆弧半径，主偏角，副偏角都由刀具决定，所以进给量（f）、切削速度（v）、背吃刀量（ap）是影响粗糙度的主要切削参数。故本文选取粗糙度为试验指标，选取以上三只能够切削参数为影响因素。

响应曲面法是一种实验条件寻优的方法，适宜于解决非线性数据处理的相关问题，它包括了试验设计、建模、模型检验及寻求最佳组合条件等实验和统计技术[3]。响应曲面法按方法可分为中心复合试验设计（CCD）和Box-Behnken试验设计。而中心复合试验设计又根据轴向点α的取值分为中心复合序贯设计（CCC），中心复合有界设计（CCI），中心复合表面设计(CCF)。对于中心复合表面设计(CCF)就是取α=1，这时在没有改变立方体原来的点的设置的前提下将轴向点设在了立方体的表面上。在CCF设计中每个因素的取值水平只有3个(-1,0,1)，而一般的CCD设计，因素的水平是5个(-α,-1,0,1,α)，这在更换水平较困难的情况下是有意义的。CCF设计的劣势是失去了旋转性。但保留了序贯性，即前一次在立方点上已经做过的试验结果，在后续的CCF设计中可以继续使用，可以在二阶回归中采用。故本文采用中心复合表面设计。

1 粗糙度预测模型

表面粗糙度预测理论模型是通过对表面粗糙度的形成过程进行研究，分析各因素对表面粗糙度的影响，建立表面粗糙度的预测模型，实现对表面粗糙度的预测[4]。

1.1 试验准备

试验时使用的车床为国产C5112单柱立式车床，该车床的主轴最高转速为200r/min，总功率为18KW，最大进给量为0.38mm/r。工件是法兰盘，加工直径为466mm，加工材料为ZCUAl10Fe3（硬度>980HB）的铸造铜合金，此材料具有高的力学性能，耐磨性和耐腐蚀性能好。刀具选择YT15，硬度大于91HRA的刀具。在试验中整个加工系统处于稳态，不研究刀具材料和参数对切削力和表面粗糙度的影响。

1.2 试验设计

文章进行试验的目的是建立粗糙度的预测模型，并验证模型的正确性。使得在实际生产中可以优化个加工参数，减少调试次数，减少次品的生成。

文章采用中心复合表面设计，α=1，为了满足预测值都有一致均匀精度，三个因子的试验点数为：立方体点8个，轴向点6个，中心点6个。设定进给量f为x1；切削速度v为x2；背吃刀量ap为x3。本试验为三因素、三水平，如表1所示。

表1 切削因素水平编码表

响应曲面法采用多元二次回归方程来拟合因素与响应值之间的函数关系故，文章有三个切削参数，故文章的表面粗糙度与切削参数之间的关系如式（1）：

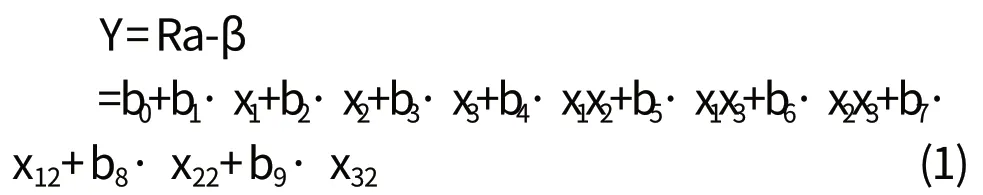
式中Y为表面粗糙度估计值；Ra为表面粗糙度；β为试验误差，bi（i=1,2,…,9）为系数的估计值；xi（i=1,2,3）为切削参数编码。

1.3 试验结果及分析

根据中心复合表面设计(CCF)试验点计划表，进行20次试验，得试验结果如表2所示。

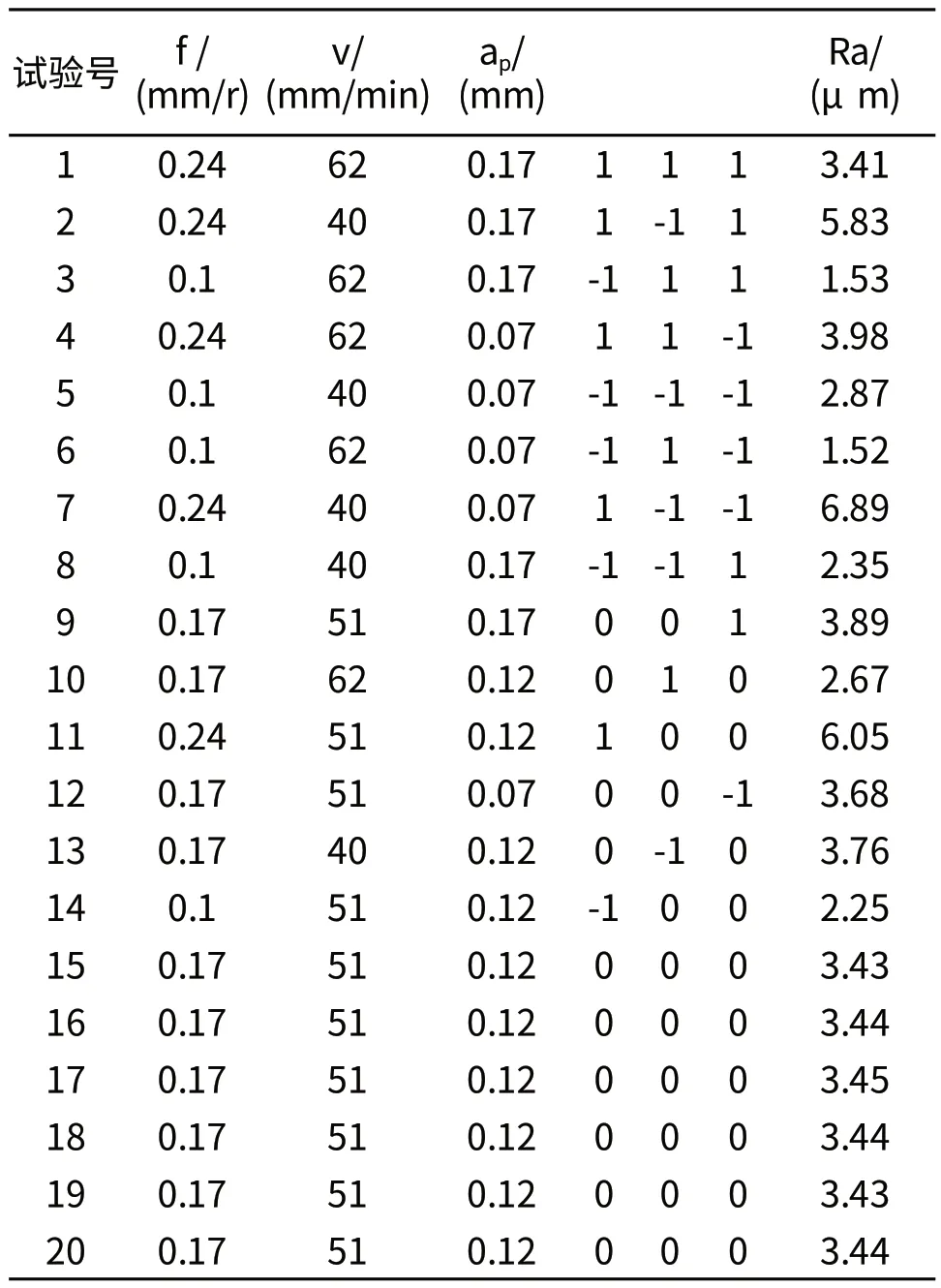
表2 试验结果

根据试验结果，用minitab软件拟合选定的模型，运用最小二乘法，得到公式（1）的系数，如公式（2）所示。

分析式（2）的有效性，得到方差分析如表3所示。残差平方即回归方程之决定系数R2=0.9338，非常接近1，故回归方程很显著。F对应的概率P接近0，α=0.05，P<α，拒绝H0，回归模型成立。

表3 方差分析表

故用响应曲面法得到的粗糙的预测模型如式（2），根据响应模型可以得到两两交互作用下的切削参数对粗糙度的影响，如图1所示。

图1 响应面模型

分析响应曲面法的曲面图，从图1（a）中可以看出在切削速度和背吃刀量的共同作用下对粗糙度的影响并不显著；从图1（b）可以看出粗糙度与进给量呈正相关关系，而背吃刀量对粗糙度基本没有影响；从图1（c）可以看出粗糙度与切削速度呈负相关关系，及切削速度增大，粗糙度减小。

在进行实际生产中，可将各加工参数的值所对应的水平值带入模型中，即可得到该切削参数组合下的表面粗糙度的估计值，从而判断该切削参数组合是否符合生产工艺要求。

2 参数优化

模型可以用来预测粗糙度，减少生产过程中的调试次数，但对于提高生产效率却并不显著，从响应曲面法得出的曲面图也不能形象的看出各切削参数对粗糙度的影响大小，故在在进行参数优化时分析各切削参数的效应和边际效应来判断各切削参数对表面粗糙度的影响。

拟合出各因素对表面粗糙度值的二次回归拟合曲线（图1），并得到各单因素子模型的回归方程：

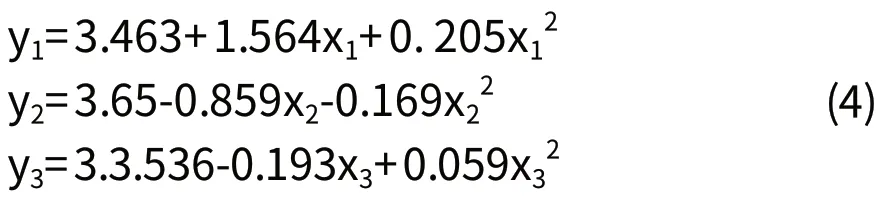
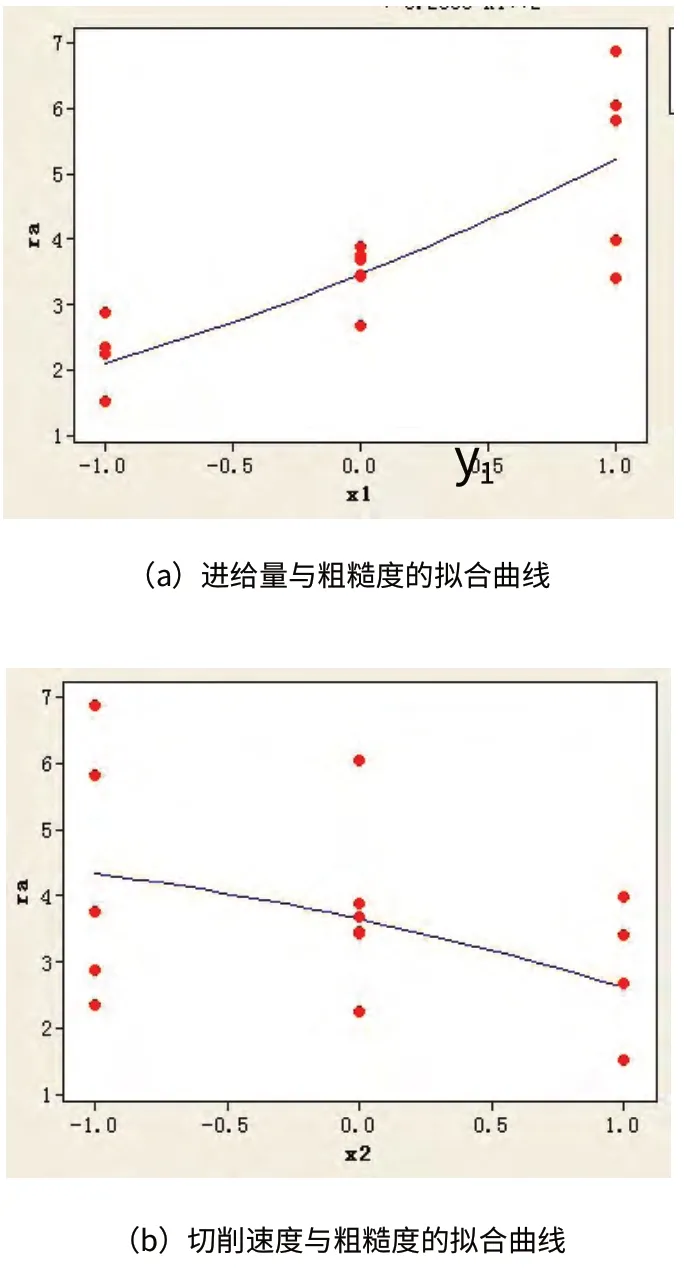
图2 表面粗糙度与各切削参数之间的拟合曲线图

从图2可以得到和图1一样的结论，但图2还不能形象的看出各因素对表面粗糙度影响程度的大小，故对方程（4）分别对各自因素求导，得出各因素在不同水平下表面粗糙度的边际方程（5），并画出边际效应图（图3）。

图3 各切削参数的边际效应图

从各切削参数的边际效应图（图3）可以看出进给量和切削速度对加工零件的表面粗糙度的影响最大，并且切削深度对粗糙度的影响很小。这三个参数对粗糙度影响程度按从大到小的顺序为：进给量（f）>切削速度（v）>背吃刀量（ap）。

机械产品单间的生产时间主要包括三部分，即准备时间、加工时间和刀具更换时间。而单件生产成本由五种成本因素组成：1) 准备费用；2) 切削费；3) 换刀费；4) 刀具费与折旧费；5) 经常费。可见无论从生产时间和生产成本来看，刀具的寿命都会影响几下加工的生产效率，故本文从切削用量对刀具的寿命的影响入手，在保证粗糙度的前提下，优化切削参数，提高刀具的使用寿命。本文是车床切削外圆，刀具的寿命公式为[5]：

式中d为工件直径，L为工件长度，A为切削余量。在本文中d=466mm，L=π·d，A=2mm。刀具使用寿命的单位为小时。

从式（6）可以看出进给量，切削速度，背吃刀量都对刀具寿命有影响。而进给量对粗糙度的影响最大，为了保证粗糙度先选择合适的进给量，本文在选定f=0.24mm/r的前提下，通过对切削速度和背吃刀量的优化来提高刀具寿命，背吃刀量的变化范围比较小，故主要影响刀具寿命的切削因素是切削速度。对公式（6）和公式（2）做刀具寿命和粗糙的等值线图，如图4所示。

图4 f=0.24mm/r时刀具寿命和粗糙度等值线图

从图4中看出当Ra=2.25μm时与刀具寿命的等值线图交于B、D、E、F四点，这表明有四组切削参数可以使粗糙度为2.25μm，但这四组切削参数的刀具寿命却不相同，E、F两点的刀具寿命为60小时，B、D两点刀具寿命为40小时。所以在保证粗糙的前提下我们可以选择刀具寿命长的切削参数组合，这样就减少刀具更换时间、换刀费、刀具费与折旧费等，从而减少加工成本，提高生产效率。故在实际生产中结合粗糙度预测模型、刀具寿命公式和实际加工条件，选择最优的切削参数组合。