川东北元坝气田须家河组主力储层参数测井精细解释

张 冲，谢润成，2，朱 涛，姚 勇，王 喻，张万茂

（1.成都理工大学 能源学院，四川 成都610059；2.成都理工大学 油气藏地质及开发工程国家重点实验室，四川 成都610059）

0 引言

前人对于储层参数解释一般都基于常规测井参数的回归拟合，解释方法单一.[1]对于储层含水饱和度解释也多是基于经验法的阿尔奇公式.[2]这些基本思路对于地层情况简单，岩性变化电性特征明显的地层效果较好，但对致密复杂性储层或者裂缝性储层的储层参数解释效果较差，解释模型不可用.由于储层参数的准确解释对于研究区天然气勘探开发评价具有重大意义，因此针对元坝气田须家河组主力储层参数进行精细解释研究，能为高效开发该地区下的气藏打下坚实的基础.

1 区域地质概况

工区位于四川盆地东北部，南为川中部低缓构造带北部斜坡，东通南巴构造带西南端、北靠近九龙山背斜南端.[3]研究区须家河组地层处于盆地内，缺少山前相，主要表现为三角洲相，沉积物在垂向剖面上表现为河道砂体与间湾泥岩互层，主力储层自上而下划分为须四段，须三段和须二段（图1）.须四段岩性表现为灰色细砂岩、粉砂岩和泥岩互层，局部夹砾岩；须三段为泥岩与粉砂岩，中—粗粒钙屑砂岩，砂质砾岩互层；须二段上、下亚段为砂岩段，中亚段为泥岩段，工区须二中亚段表现为一黑色“腰带子”.

2 储层物性参数单参数拟合模型

孔隙度和渗透率是反映储层物性特征的一个重要参数.孔隙度的准确计算也是保证其它储层参数计算精度的前提.常规测井确定地层孔隙度主要基于三孔隙度测井系列.三条孔隙度测井曲线可能对不同地层条件下孔隙度的分辨能力存在差异，因此单独对须家河组三个主力储层孔隙度进行分开解释.以常规岩心分析孔隙度为依据，模型建立前将岩心分析孔隙度与单井常规测井曲线深度归位校正，再把声波时差测井值、密度测井值、中子测井值与岩心孔隙度进行单参数拟合回归（图2）.在进行渗透率与声波时差、中子、密度曲线的相关性分析时，发现无论是按地质模型结果还是按岩性分类结果，其相关性都不是很理想，只有和孔隙度之间的相关性较好，因此可基于元坝气田须家河组主力储层岩心物性测试资料建立渗透率解释模型（图2）.由此可建立各层单参数物性解释模型（表1），该解释方法对岩心分析测试要求较高，渗透率解释模型由于是实测与实测资料的相关性拟合，推广效果受到孔隙度与测井模型精确程度的影响.

图1 元坝气田须家河组地层简表

图2 元坝气田须三段孔隙度和渗透率单参数拟合模型

3 “多元回归”储层参数解释模型

多元回归基本理论基于对引入变量相关性验证和处理的数学统计方法，其基本思想是：引入自变量与目的变量之间无确定或者严格的函数关系，但可以根据引入自变量特征分析、效验，发现能对目的变量进行表征的数学表达式.该原理基本任务是根据目的变量和多个引入自变量的实际观测结果，采用最小二乘法，构建目的变量对多个引入自变量的多元回归模型.[4]图3表示须四段79个测试样本应用多元回归方法进行物性参数解释，精选3个常规测井分析参数（声波时差，中子孔隙度，体积密度）与实测孔隙度进行回归拟合，通过回归过程中标准化残差分析和回归标准化残差的概率分析，建立了相应的孔隙度多元线性拟合模型，拟合相关程度高.由于工区渗透率受裂缝影响较大，裂缝影响下的储层渗透率不代表储层基质自身的渗透能力，因此不适用于回归分析.依据多元回归分析原理，可推广建立元坝气田须家河组各主力储层的孔隙度和含水饱和度的多元回归解释模型（表1）.

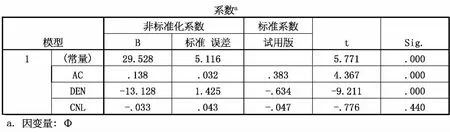
图3 元坝气田须四段多元回归孔隙度解释模型

4 “阿尔奇”含水饱和度解释模型

用常规测井信息解释储层中含水饱和度，国内外对此进行过许多研究，虽然解释含水饱和度的经验公式千差万别，考虑因素也各不相同，但基本解释方法均主要在岩石饱含水的条件下，基于并联导电思想推导出来的，其实对这些公式的改进也是阿尔奇经典公式派生推演的产物.[5]针对元坝气田须家河组主力储层，可采用阿尔奇模型[6]对该地区含水饱和度进行解释.

地层水电阻率（Rw）和阿尔奇饱和度模型岩电参数（a、b、m和n）是确定储层中含水饱和度的关键参数，在不同的地层、岩性，这些参数是各不相同的.[7]该地区的含水饱和度，必须依据所研究地层的具体情况，根据元坝地区主力储层须三和须二段实际的水分析资料和岩心岩电实验分析资料确定.

4.1 地层因素系数a和胶结指数m的确定

据经典的阿尔奇地层因素关系式：[8]

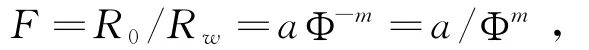
R0—饱含地层水的岩石电阻率，Rw—岩石中饱含地层水的电阻率（取0.05Ω·m）.

对上述关系式两边取对数得：

由此可见，地层因素和孔隙度在双对数坐标下基本关系为一条直线，该直线在Φ＝1时的纵坐标为Log（a），其斜率为m.须二段和须三段地层因素与孔隙度的回归关系效果较好，相关系数比较高，故模型确定须三段岩石胶结指数 m＝1.3076，岩性有关的岩性系数a＝1.273；须二段岩石胶结指数m＝1.2797，岩性有关的岩性系数a＝0.9645（图4），须四段储层由于未进行岩电参数实验，可借鉴须三段储层确定的阿尔奇岩电参数.

4.2 电阻增大率系数b和饱和度指数n的确定

据阿尔奇经典的电阻增大率关系式：I＝Rt／Ro＝b／Swn，Sw指岩石含水饱和度，Rt指含油气岩石的电阻率.对上述关系式两边取对数得：

Log（I）＝log（b）-n＊log（Sw）

由此可见，在双对数坐标下I一Sw关系为一条直线，该直线在Sw＝1时的纵坐标为log（b），其斜率为n.据此可以确定出电阻增大率系数（b）和饱和度指数（n）（图5）.须三段和须二段含水饱和度与电阻率指数的交会图，回归效果较好，相关系数很高，可据此确定研究区须三段电阻增大率系数b＝0.9949，饱和度指数n＝1.2797；须二段电阻增大率系数b＝1.014，饱和度指数n＝1.3387，同理须四段可参考须三段确定的参数.根据阿尔奇经典含水饱和度计算公式可得到元坝气田须家河组主力储层的含水饱和度解释模型（表1）.

图4 元坝气田须家河组主力储层含水饱和度与电阻率指数交会图

图5 元坝气田须家河组主力储层含水饱和度与电阻率指数交会图

5 “BP神经网络法”储层参数解释模型

“BP神经网络”算法主要基于“最速下降法”的一种优化方法.在元坝气田储层参数解释的实际应用中，主要采用了基于Levenberg-Marquardt算法（LM），也被称为阻尼最小二乘算法，该算法应用于储层参数预测，可取得良好的效果.[9]BP神经网络由输入层，隐含层和输出层组成，通过测试样本学习和检验，建立最优的BP神经网络解释模型.在研究中，设计的BP神经网络结构主要为输入层、隐含层、输出层三层.[10]经过多次试验，含水饱和度参数解释选取了声波时差（AC），中子孔隙度（CNL），补偿密度（DEN），深侧向电阻率（RD）以及自然伽玛（GR）这5个测井参数组合作为神经网络的输入.输入结点为5个，根据隐含层结点个数大约为输入结点的两倍关系，隐含层取10个结点，输出层取1个结点，这1个输出为含水饱和度计算值（图6）.BP神经网络解释含水饱和度时，将样本分为两组：训练样本和检验样本.考虑到须四段样本数，故将样本全部作为训练样本.须二，须三和须四段的训练样本解释的含水饱和度与岩心实测的含水饱和度相关性非常好，须二和须三检验样本计算的含水饱和度与实测含水饱和度相关性也较好（图7，图8），该BP模型可用于研究区须家河组主力储层含水饱和度解释.孔隙度和渗透率BP模型也依据该原理，输入参数中孔隙度解释使用AC，DEN，CNL；由于BP检验效果非常好，因此渗透率BP模型则除了三孔隙度测井参数外还引用了BP解释的孔隙度四个参数作为输入参数.表1显示了元坝气田须家河主力储层各层位利用BP网络进行各储层参数解释的模型构成.

图6 BP神经网络结构及计算学习界面

图7 须二段BP含水饱和度与岩心含水饱和度学习样本和检验样本交会图

图8 须三段BP孔隙度与岩心孔隙度学习样本和检验样本交会图

6 储层参数解释模型优选

元坝气田须家河组主力储层，岩性电性特征复杂，给储层参数解释造成一定困难，对储层物性参数进行单一测井参数与实测岩心物性资料回归和多参数多元线性回归建立相应模型，并考虑非线性BP网络法对须家河组主力储层物性参数进行解释.多种方法的对比分析利于研究区储层物性参数解释准确性的提高.通过与未参与模型建立的实测参数进行对比，单参数物性解释模型精度最低，多元回归模型精度较高，而BP神经网络非线性解释模型的解释精度最高（图9）.针对储层含水饱和度解释，据岩电参数测试资料利用阿尔奇经验公式，多元回归方法和BP非线性解释原理建立了含水饱和度多种解释模型，效果最好的依然是非线性BP模型.而阿尔奇含水饱和度模型，在进行地区岩电实验的情况下，其解释模型无论与实测资料在值大小还是趋势比较均无吻合性（图10）.因此在对研究区进行储层参数测井解释时，可考虑使用最优的BP神经网络进行含水饱和度计算.

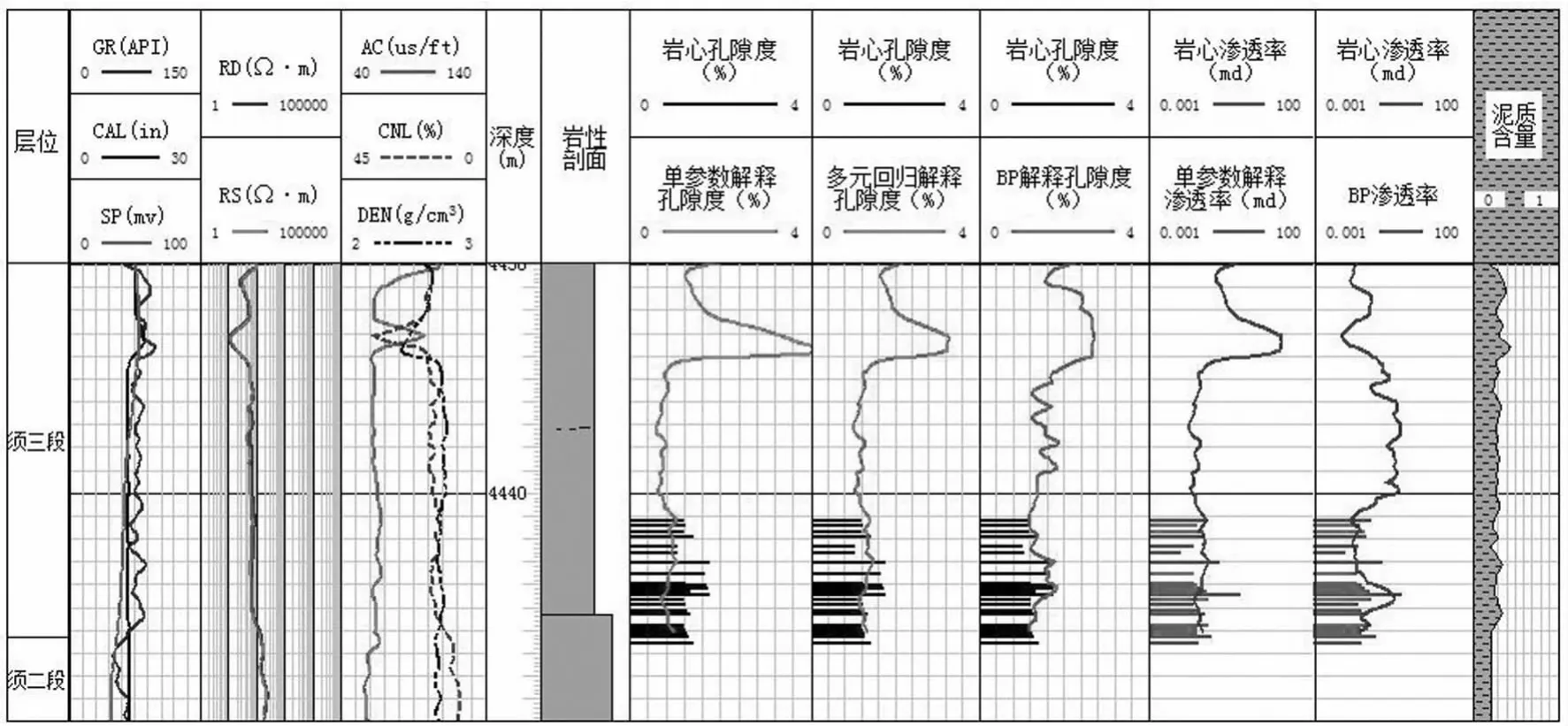
图9 须三段不同孔隙度和渗透率模型解释对比图（元坝6井）

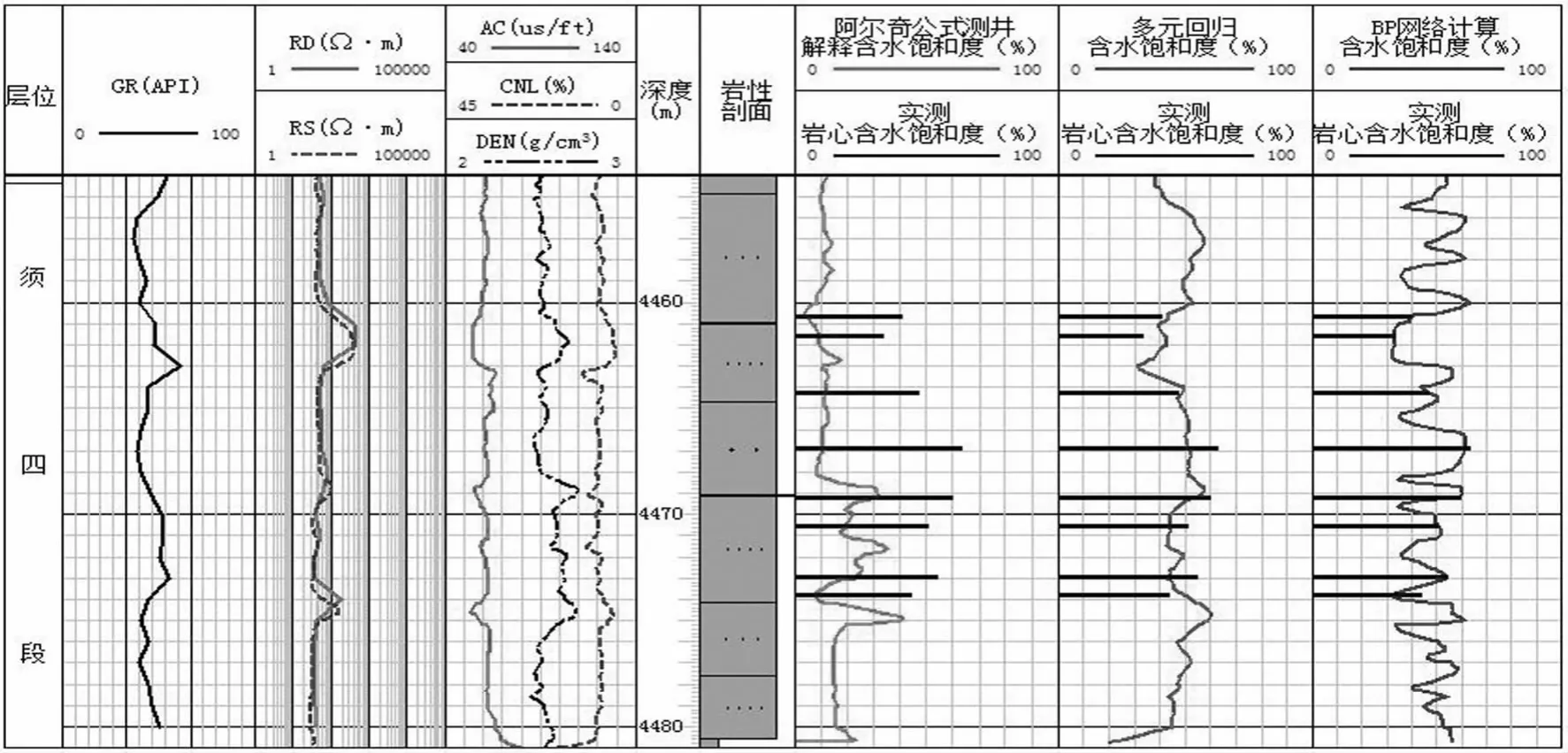
图10 须四段不同模型解释含水饱和度对比图（元陆1井）

表1 元坝气田须家河组主力储层参数解释模型

7 结论

元坝气田须家河组主力储层，岩性电性特征复杂，含气特征分布不清，储层参数进行纵向剖面解释是搞清楚储层含气潜力的重要手段.考虑到工区地层的复杂条件，依据常规测井和储层参数测试资料单参数拟合，多元线性回归，含水饱和度阿尔奇经验解释法和BP神经网络储层参数计算模型进行综合解释，“BP网络模型”非线性特性显示出了良好的解释效果.因此，在对元坝气田须家河组主力储层进行储层参数解释时，主要考虑非线性网络计算方法，结合其他解释模型综合进行储层参数解释，可以在最大程度上提高解释精度，为进一步开发评价奠定坚实基础.

[1]周 磊，范姗姗，冻伟中.柯东地区储层测井解释方法研究[J].石油天然气学报，2013（2）：111-116.

[2]郑庆林，王钰森，赵 雨.低孔隙度条件下阿尔奇含水饱和度解释模型改进[J].测井技术，2006（1）：57-59.

[3]王 喻，谢润成，周 文，等.元坝须二段储层四性特征及关系研究[J].科学技术与工程，2013（12）：3410-3415.

[4]王洪辉，黎 鹏，段新国.四川盆地须家河组低孔致密砂岩孔隙度测井解释研究[J].成都理工大学学报：自然科学版，2009（3）：250-252.

[5]王 鹏，赵玉莲，韩 琳.乌尔逊凹陷凝灰质砂岩储层含水饱和度计算[J].岩性油气藏，2010（1）：114-118.

[6]雍世和，张超谟.测井数据处理与综合解释[M].东营：石油大学出版社，1996：270.

[7]刘向君，刘 洪，杨 超.碳酸盐岩气层岩电参数实验[J].石油学报，2011（1）：131-134.

[8]刘忠华，吴淑琴，杜宝会，等.储层渗透性与地层因素关系的实验研究与分析[J].地球物理学报，2013（6）：2088-2097.

[9]邹 玮，李 瑞，汪兴旺.BP神经网络在致密砂岩储层识别中的应用[J].石油工业计算机应用，2006（2）：19-25.

[10]汪志红，张银德，周 文，等.利用BP网络技术预测碳酸盐岩储层孔隙度[J].物探化探计算技术，2005（1）：20-24.