试探粒子模型下托卡马克中逃逸电子的能量极限分析

竹锦霞，涂 朴

（四川文理学院 物理与机电工程学院，四川 达州635000）

0 引言

所谓逃逸电子，是指一部分速度大的热电子或者是快电子受到的碰撞阻力小于电场力时，超过一定阈值后不断被加速到很高的能量的电子.由于逃逸电子的能量可高达数十MeV，当它轰击装置第一壁材料时，对装置的安全构成了严重威胁.[1-2]特别是在托卡马克等离子体低密度放电和破裂阶段，研究逃逸电子能量极限，探索有效的抑制能量的手段，是下一代装置稳定运行的基础之一.[3]

试探粒子模型是分析逃逸电子行为的有效工具.[4-5]利用试探粒子模型可以研究包括电场加速、本底等离子体的碰撞、同步辐射损失下逃逸电子的能量极限.本文利用试探粒子模型研究了HT-7托卡马克中限制相对论逃逸电子的能量机制，包括电场加速、同步辐射损失、轨道漂移、逃逸电子和磁场波纹共振以及MHD不稳定性.

1 逃逸电子能量极限分析

在托卡马克装置中，当电子超过阈值速度时会不断被环形电场加速并且可能达到几十MeV的能量.电子最终所获得的最大能量受到以下几个方面限制：同步辐射的减速、轨道漂移、逃逸电子和磁场波纹之间的共振、不稳定性.当逃逸电子损失的能量平衡等于从电场中获得的能量时，逃逸电子的能量达到最大值，即极限值.托卡马克变压器的伏秒数表示逃逸电子可以吸收的能量大小.其中同步辐射引起的能量损失是主要项，磁场纹波等对逃逸能量的限制也有很重要的作用.

在托卡马克装置中，逃逸电子受环形电场的加速作用，电场对单个电子做功的功率为

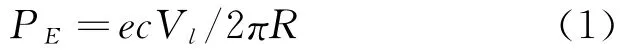
式中R是装置的大半径，e是电子电荷，Vt是等离子体环电压，c是光速.

电子获得的电场能量随时间的演化关系为

等离子体辐射是等离子体自身固有的现象.逃逸电子在装置中做环向运动时辐射电磁波，辐射方向在逃逸电子运动的前方，波长在几个微米范围.逃逸电子在装置中做环向运动时辐射电磁辐射，单位立体角内的功率为

式中β ≡v／c，γ＝（1-β2）-1／2

在相对论极限时，β≈1.当1-βcosθ取极小值时辐射功率取得最大值.其辐射功率为

re是电子经典汤姆逊半径，γ是相对论因子，Rc为逃逸电子运动轨迹的半径.

带电粒子在均匀恒定磁场中的运动由以下条件决定：沿磁场方向的电场分量引起的加速运动、E×B引起的漂移运动、垂直于磁场的回旋运动.托卡马克中，磁场强度并不是均匀分布的.只有当逃逸电子的轨道半径和位移偏移小于装置的小半径时，逃逸电子才可以约束在装置中，否则会和第一壁或者限制器碰撞而损失.约束的逃逸电子的最大能量为

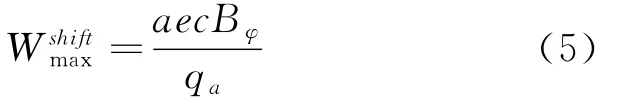
式中qa是等离子体边界的安全因子，a是等离子体的小半径.

根据HT-7上qa＝4，BØ＝2T，a＝0.27m ，对应于所能约束的最大能量约为40MeV.

在托卡马克装置上由于磁场是由有限的线圈形成，磁场有一定的波纹度，并且波纹是随等离子体半径的增大而增大的，逃逸电子在经历这个波纹场时会受到调制，调制频率为：

n是磁场波纹的谐波阶数，Nt是纵场线圈的个数，R是装置的大半径，c是光速.

如果电子的回旋运动和n次谐波共振，电子会被散射，增大pinch角，大的pinch角会增加辐射损失影响能量极限，它取决于n和波纹大小.此共振作用随谐波次数的增加而减弱.利用这种共振作用可将逃逸电子的能量约束在一定的低能范围内，有利于对高能逃逸电子能量的控制.另外除了磁场波纹的大小，环电压是影响共振的一个重要因素，高的环电压可以克服高阶模式的能量共振，从而达到更高的能量，直到某一个谐波次数起明显作用.发生n次谐波共振的条件主要取决于电场的大小，波纹的大小.

由于非Maxwellian分布的高能成分的自由能可以通过共振和等离子体振荡.当达到阈值能量，就会发生不稳定性.不稳定性将影响逃逸电子的能量极限以及约束时间.[6]

逃逸电子在电场中的加速和同步辐射阻尼是影响电子能量限制的主要因素.在轨道漂移、逃逸电子和磁场波纹之间的共振、不稳定性等因素影响下逃逸电子的能量演化为

图1为利用试探粒子模型结合HT-7放电过程中环电压值计算得到的逃逸电子能量演化图（θ＝0.2）.从图中可以得到本次放电过程中逃逸电子的最高能量值大约为25MeV.

图1 试探粒子模型下逃逸电子能量随时间变化关系（Θ＝0，2，Vf＝0.8V）

当PE-P＝0时逃逸电子达到能量平衡，对应的能量以相对论因子表示为

图2为根据不同等离子体参数Θ计算得到的逃逸电子平衡能量图（环电压Vl分别取1V，2V）

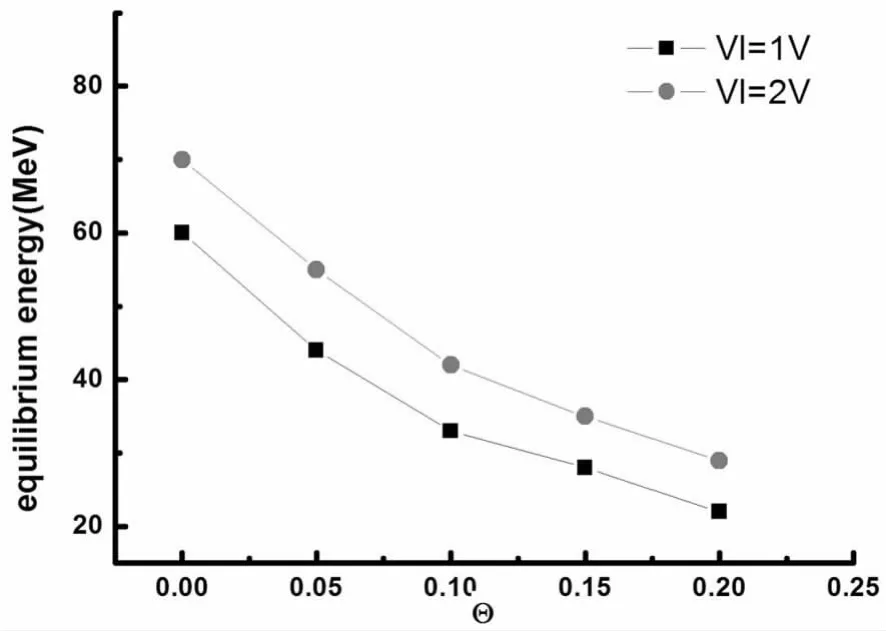
图2 逃逸电子平衡能量图

从图2中可以看出逃逸电子的能量极限除了和不同等离子体参数有关外，Θ角对能量极限值影响很大.

2 总结

托卡马克中高能逃逸电子释放的能量对装置第一壁材料的性能和寿命都会带来严重的危害.本文利用试探粒子模型分析了HT-7托卡马克中限制相对论逃逸电子能量机制，包括电场加速、同步辐射的减速、轨道漂移、逃逸电子和磁场波纹之间的共振、不稳定性等.得到了高能逃逸电子的能量时演关系以及不同参数下的平衡能量值.

[1]R.Jaspers，K.H.Finken，G.Mank，et al.Experimental investigation ofrunaway electron generation in Textor[J].Nucl.Fusion，1993（33）：1775-1785.

[2]I Entrop，N J Lopes Cardozo，R.Jaspers，et al.Diffusion of runaway electrons in TEXTOR-94，Plama Phys[J].Control Fusion，1998（40）：1513-1527.

[3]Jasper S R，Lopes Cardozo N J，Schuller F C，et al.Disruption generated runaway electrons in TEXTOR and ITER[J].Nucl.Fusion，1996（36）：367-373.

[4]Martin-Solis J.R.Momentum-space structure of relativistic runaway electrons[J].Phys.Plasmas，1998（5）：2370.

[5]Martin-Solis J.R.Energy limit on runaway electrons in tokamak plsamas[J].Phys.Plasmas，1999（6）：238-252.

[6]I.Entrop.Confinement of relativistic runaway electrons in tokamak plasmas[D].PhD thesis，Eindhoven University of Technology，Netherlands，1999：27-30.