镁合金不同取向多枝晶生长相场法模拟

尧军平，李翔光，龙文元，张 磊

(1.南昌航空大学 轻合金加工科学与技术国防重点学科实验室，南昌 330063；2.School of Engineering, The Ohio State University, Columbus, OH 43210, USA)

作为目前实际应用最轻的金属结构材料，镁合金具有比强度和比刚度高、密度小(1.75～1.90 g/cm3)、阻尼性和切削加工性好等优点，用镁合金生产的铸件具有优良的减振和降噪性能、耐磨性能、低惯性能、电磁屏蔽性、易回收特性等，被赞誉为21世纪的“绿色”工程材料，在电子、汽车和航空工业领域有广泛的应用[1-3]。镁合金铸件的力学性能强烈依赖于其在凝固过程中所形成的显微组织，枝晶是镁合金最常见的凝固显微组织，其形貌特征决定着镁合金铸件的力学性能。采用微观组织数值模拟能够获得镁合金枝晶形貌、微观偏析等方面的信息，进而对镁合金的力学性能进行预测，并据此调整优化生产工艺，从而得到力学性能更优良的铸件。

微观组织模拟的方法主要有确定性方法、CA法和相场法等。相场法由于在微观组织模拟方面的综合优势，已成为国内外微观组织模拟的热点。目前，学者所进行的微观组织模拟绝大部分是针对具有 FCC晶胞的金属(例如Ni、Al和Cu)。而镁合金是典型的HCP晶体结构，具有不同于FCC结构晶体的各向异性特征。因此，要对镁合金枝晶生长行为进行模拟就必须建立适合HCP晶体结构金属的数值模型。在镁合金微观组织相场法模拟方面，EIKEN等[4-6]对镁合金进行了二维、三维以及定向凝固微观组织的模拟。CHAWLA等[7]和WANG等[8]对镁合金三维等轴晶的生长进行了模拟。MONTIEL等[9]对镁合金焊接条件下的微观组织进行了模拟研究。缪家明等[10]研究了模拟参数对镁合金枝晶生长过程的影响。袁训锋等[11]基于WHEELER等[12]提出的模型研究了强迫对流对镁合金枝晶生长行为的影响。

就实际凝固过程而言，一般情况都是多晶粒共同生长的，并且晶粒的结晶取向并不一致。不同取向多枝晶生长的模拟采用多相场模型是比较合理的，但多相场模型的一个明显缺点是变量太多，每一个晶粒都需要一个单独的相场控制方程，这将引起计算空间和计算量数倍甚至数十倍的增加，如果在模型中再耦合温度场和流场，其计算量将更为巨大。为了实现对不同取向多枝晶生长的模拟并减少计算量，本文作者将基于KIM等[13-15]提出的KKS相场模型(相比WBM模型，该模型消除了WBM模型中的附加势垒，计算效率更高，并且该相场模型可以通过耦合真实的热力学数据库来模拟实际合金的凝固)，根据 KOBAYASHI等[16]提出的描述晶粒取向的方法，建立一个新的相场、溶质场、流场、温度场以及取向场相耦合且适合于模拟HCP晶系镁合金多枝晶生长的相场模型，并采用该模型对纯扩散和强迫对流作用下的镁合金多枝晶生长行为进行模拟研究。

1 相场模型

1.1 相场控制方程

在KKS相场模型的基础上耦合晶粒取向后，自由能函数变为

式中：区域自由能密度f(φ,c,T)=h(φ)fS(cS)+[1-h(φ)]fL(c)+wg(φ)；相场变量φ=0代表液态，Lφ=1代表固态；cS和cL分别代表固相和液相中的溶质浓度；固液混合浓度c=h(φ)cS+[1-h(φ)]cL，fS(cS)和fL(cL)分别为固相和液相中的自由能密度，在界面区域内固相和液相的化学势相等，即fS[c(x,t)]=cSSfcLL[cL(x,t)]，h(φ)为势函数，h(φ)=φ3(10-15φ+6φ2)，g(φ)为剩余自由能函数，g(φ)=φ2(1-φ)2，wg(φ)为界面的过剩自由能，fori为空间取向错配引起的能量变化，fori=Hh(φ)|∇θ|，H为调节取向能错配大小的参数，θ为取向场，代表结晶取向，在每一个晶粒内部θ为0到1之间的某个定值，在液相中随机变化。根据经典线性不可逆热力学，相场变量φ随时间的变化假设与自由能函数的变化成正比，即有

将自由能函数(1)代入式(2)，并利用稀溶液近似处理，可得：

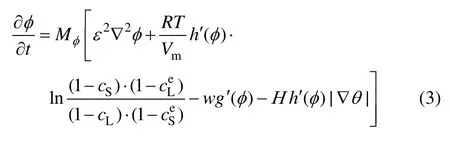
式中：c为溶质浓度；上标e表示平衡状态；下标 S和L分表表示固相和液相；R是摩尔气体常数；T是热力学温度；Vm是摩尔体积；Mφ是与界面动力学有关的相场参数。

为了考虑界面能各向异性，并适应六重对称性镁合金的求解，可将梯度项系数ε表示为

式中：ϑ为界面法向与x轴的夹角；ε0为梯度项系数ε(ϑ)的平均值，ϑ=arctan(φy/φx)；2πθ/m代表主轴生长方向与x轴之间的夹角；k为各向异性的模数，表示系统的对称次数，其值取6；v为各向异性强度。引入界面能各向异性后，方程(3)变为

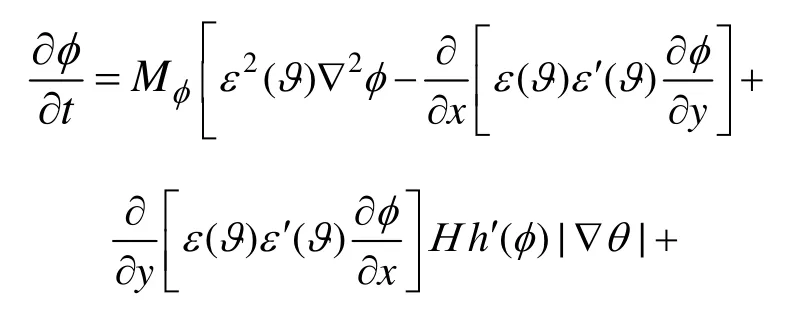
1.2 质量和动量方程

质量守恒方程(连续性方程)如下：

动量守恒方程如下：

式中：V为速度矢量，假设Vx为x轴方向的分速度，Vy为y轴方向的分速度，则；p为压力；ρ表示密度，假设液相和固相的密度相等；μ为动力学粘度；单位体积界面散耗力，h取值2.757。

由上可知，几内亚BOFFA矿区的坐标系统应为：采用Clarke1880参考椭球，投影采用6°分带的UTM投影，中央子午线为西经15°，测区将抵偿高程面改到1 498 m。高程基准为WGS-72大地水准面。

1.3 溶质场控制方程

保守的溶质场随时间的演化满足Cahn-Hilliard方程，耦合流场的溶质场扩散方程在数学上表示为

将式(1)代入式(8)后，可得：

式中：Mc为溶质场可动性系数；D(φ)为体系的溶质扩散系数，D(φ)=DL+h(φ)(DS-DL)；DS和DL分别固、液相中的溶质扩散系数。

1.4 取向场控制方程

非保守的取向场θ随时间的演化满足 Ginzburg-Landau方程，在数学上表达为

将式(1)代入式(10)后，则有

式中：Mθ为取向场场可动性系数；H为调节取向能错配大小的参数。

1.5 温度场控制方程

耦合流场后，温度场控制方程表示为

式中：T为热力学温度；L为潜热；cp为定压比热容；D为λ/(ρcp)，λ为导热系数。

1.6 扰动

扰动可引发枝晶侧向分枝的生长，为了模拟实际凝固过程中界面处的波动和二次或更高次枝晶的生长，本研究在溶质扩散方程中加入随机扰动，即：

式中：χ为在-1～+1之间取值的随机数，ω˙为与时间有关的扰动强度因子。

2 计算求解

2.1 材料物性参数

模拟所用AZ91D镁合金物性参数如表1所示[17]。

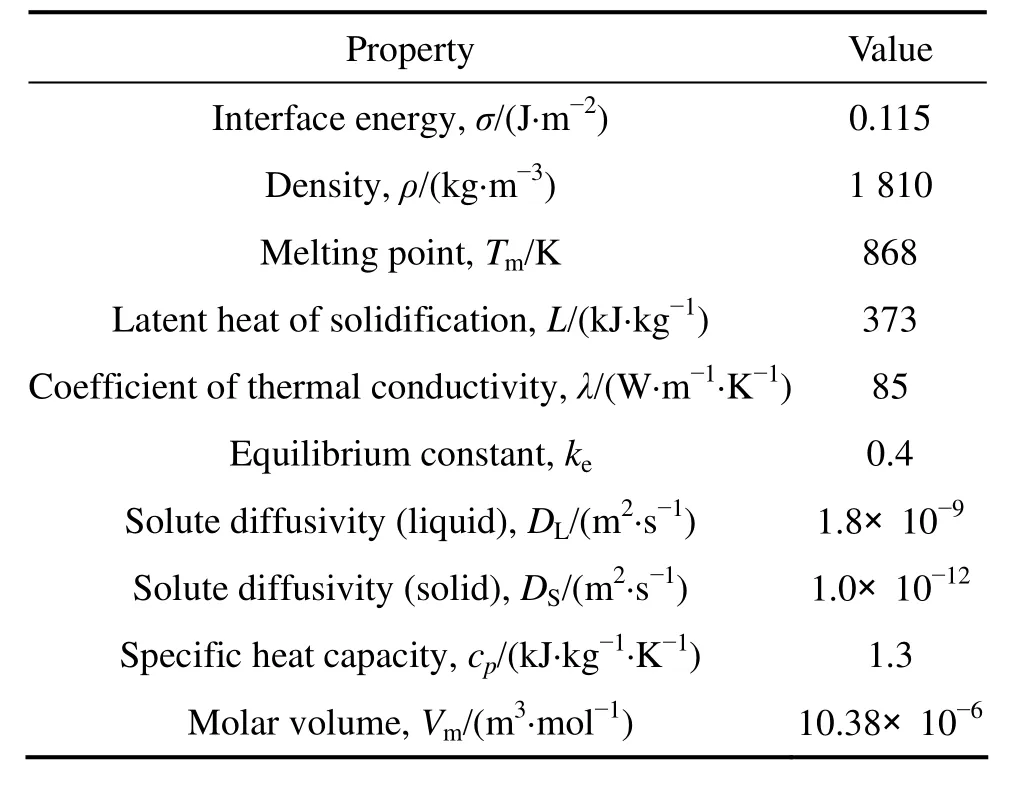
表1 AZ91D镁合金物性参数Table1 Physical properties of AZ91D magnesium alloy

需要说明的是，为简化问题，模型中忽略了导热系数λ随温度的变化。

2.2 数值计算方法

采用显示有限差分法求解相场控制方程(5)、溶质场控制方程(9)和取向场控制方程(11)；采用simple算法求解质量守恒方程(6)和动量守恒方程(7)；采用交替方向隐式差分法(ADI)求解温度场控制方程。避免了时间步长的限制，计算时间步长Δt=Δx2/5DL，相场、溶质场、流场和取向场的网格尺寸为Δx=Δy= 1.0×10-8m。由于合金的热扩散系数是其溶质扩散系数的几百倍，为了减少计算量，取温度场的网格尺寸为溶质场网格尺寸的10倍，即网格尺寸为1.0×10-7m。在计算区域的边界上，温度场采用定温边界条件，相场、流场、溶质场、取向场及压力场均采用Zero-Neumann边界条件。

3 模拟结果与分析

3.1 纯扩散时的多枝晶生长形貌与溶质分布

图1所示为纯扩散时具有不同择优生长取向角的多枝晶生长形貌(见图1(a)和(c))和溶质分布情况(见图1(b)和(d))。为便于研究，初始晶核位置和择优生长取向角均由人工预先设定，中心晶核A的择优生长取向角为0°，初始温度为765 K。如图1(a)和(b)所示，枝晶生长初期，在枝晶相互碰撞接触前，晶粒间无相互影响，其形貌与单个枝晶生长时的形貌是相同的，以晶粒A为例，在{0001}基面上，整个枝晶沿着20〉晶向以对称形式生长，一次枝晶主干间互成60°夹角，一次枝晶干与该主干上的二次枝晶臂间也约成 60°夹角。贫Al区主要集中于一次枝晶干和二次枝晶臂的轴对称中心位置，这主要是由于凝固过程枝晶尖端曲率效应引起过冷，使固相线向下移动，而固相中溶质的扩散速度又远远落后于枝晶的生长速度。在液固界面前沿出现了溶质Al的富集。这主要是由于镁合金的凝固属于非平衡结晶过程，合金在凝固过程中需要对溶质进行再分配，这导致固相中溶质的浓度低于初始浓度，而液相中溶质的扩散速度也要小于枝晶生长速度，凝固析出的溶质不能及时充分地扩散到液相中，从而在枝晶前沿富集。随着凝固的进行，如图1(c)和(d)所示，枝晶间开始相互影响，在相互接触碰撞的区域(见图1(d)中方框所选区域)，主枝的生长受到明显抑制，枝晶尖端变秃。这主要是由于枝晶相互接触的界面上，凝固析出的溶质和释放的潜热的扩散通道在相互碰撞枝晶的夹击下而变得弯曲狭长，这严重阻碍了溶质和热量的扩散，凝固析出的溶质和释放的热量在此富集造成了该区域实际过冷度的减小从而抑制了枝晶的生长。如果生长前沿不受阻碍，枝晶臂仍会继续向过冷液相中伸展，因此，虽然在碰撞前枝晶具有规则的六重对称形状，但最终也会遭到破坏而形成不规则的枝晶形貌。同时，由于晶粒的结晶取向并不一致，各晶粒所受到的碰撞不同，这导致各晶粒最终的枝晶形貌也就不相同。

图1 纯扩散时多枝晶生长在不同时刻的枝晶形貌和溶质分布Fig.1 Dendritic morphologies((a),(c))and distributions of solute ((b),(d)) for multiple grains growth without flow at different times:(a), (b) t=5 000Δt; (c), (d) t=9 000Δt

在实际凝固过程中，晶粒的形核是连续的并且晶粒的结晶取向也是随机的。图2所示为镁合金的晶粒形核与生长过程。为了简化问题，设定最大形核个数，并假设形核速率为一定值。由图2可见，随着凝固的进行，晶核数目逐渐增加，但达到一个最大值时，晶粒的数目并不再增加，这最大值是由设定的最大形核个数决定。各晶粒间竞争形核与生长，晶粒的结晶取向并不一致，先形核的晶粒由于拥有足够的生长空间，生长出了发达的二次枝晶，而后形核的晶粒由于受生长空间、先形核晶粒生长所析出溶质和释放潜热的影响，其一次枝晶臂或二次枝晶臂生长速度减慢并最终提前结束生长。在晶粒相互碰撞的区域，溶质的扩散通道变得弯曲而狭长，溶质的扩散受阻，溶质浓度高，这导致这些区域的实际过冷度减小，区域的熔点降低，其凝固比其他区域慢，从而最终在这些区域形成晶界。

3.2 强迫对流作用下的多枝晶生长形貌与溶质分布

图3所示为强迫对流作用下镁合金多枝晶生长的枝晶形貌和溶质场分布情况。水平流速v=0.01 m/s，其他初始条件与图1相同。如图3(a)和(b)所示，枝晶相互碰撞前，晶粒各自生长，晶粒间相互影响较弱，枝晶形貌与相同初始条件下的单个枝晶生长的形貌相同，上游方向一次枝晶臂最长，上游侧与水平方向呈60°夹角的两枝晶臂次之，下游侧与水平方向呈60°夹角的两枝晶臂较短，下游方向枝晶臂最短。这是由于过冷熔体流过晶粒，将凝固析出的溶质和释放的潜热从枝晶的上游冲刷到下游并在下游富集，这样就使得枝晶上游的热过冷度和成分过冷度都增大，促进枝晶的生长，而枝晶下游区由于溶质和潜热的富集，热过冷度和成分过冷度都减小，枝晶生长受到明显抑制。随着枝晶的生长，如图3(c)和3(d)所示，晶粒A、B、C、D、E的溶质场和温度场相互碰撞重叠。由于枝晶B、D以及枝晶A、B、D分别有效阻挡了过冷熔体对枝晶A和枝晶C、E的冲刷以及枝晶间的碰撞使得溶质扩散通道变得狭长，在枝晶A和枝晶C、E上游侧发生碰撞接触的区域形成了局部溶质富集区(图3(d)中所框选区域)，这使得这些区域实际过冷度减小，其枝晶臂的生长速度减小甚至停止生长，枝晶干尖端变秃。在枝晶生长前沿不受阻碍的区域，枝晶臂则仍会继续向过冷熔体中伸展，枝晶形貌与相同初始条件下的单枝晶生长形貌不再相同。

图4所示为AZ91D砂型铸件在光学显微镜偏振光下的枝晶结构。由图可以看出，镁合金枝晶生长表现出显著的密排六方结构，6个一次枝晶臂之间约成60°夹角，相向生长的枝晶互相影响竞相生长，不同枝晶的一次晶臂彼此抑制，各一次晶臂长度存在很大差异，拥有发达的二次枝晶臂，枝晶形貌不具有对称性。可见，图3(c)所示的强迫对流作用下镁合金多枝晶生长形貌的模拟结果与实验结果是十分相似的。

3.3 多枝晶生长行为定量分析

为进一步分析纯扩散时和强迫对流作用下多枝晶生长行为，分别计算了纯扩散时以及强迫对流作用下多枝晶生长在不同时刻的枝晶尖端生长速度，并与相同模拟条件下纯扩散时和强迫对流作用下单枝晶生长的枝晶尖端生长速度进行比较，其结果如图5所示。由图5可看出，各枝晶尖端生长速度都比较平稳，这是由于温度场采用的是定温边界条件，潜热的释放并不会使模拟区域的温度发生大的变化。各稳态枝晶尖端生长速度的具体大小关系为vtip1＞vtip2＞vtip3＞vtip4＞vtip5＞vtip6(其中vtip1～vtip6分别表示单枝晶上游尖端、多枝晶上游尖端、纯扩散下单枝晶尖端、纯扩散下多枝晶尖端、单枝晶下游尖端、多枝晶下游尖端的稳态生长速度)。

图2 纯扩散时连续形核多枝晶生长在不同时刻的溶质分布Fig.2 Distributions of solute for multiple grains growth without flow at different times used continuous nucleation model: (a) t=5 000Δt; (b) t=10 000Δt; (c) t=15 000Δt

图3 强迫对流作用下多枝晶生长在不同时刻的枝晶形貌和溶质分布Fig.3 Dendritic morphologies((a),(c))and distributions of solute ((b),(d)) for multiple grains growth without flow at different times:(a), (b) t=5 000Δt; (c), (d) t=8 000Δt

图4 砂型AZ91D铸态的微观组织[18]Fig.4 As-cast microstructure of sand mould AZ91D casting polarized light[18]

图5 枝晶尖端生长速度与凝固时间的关系Fig.5 Relationship between tip velocity and solidification time

计算了纯扩散时和强迫对流作用下多枝晶生长时的固相率变化曲线，结果如图6所示。从图6中可看出，纯扩散时和强迫对流作用下多枝晶生长时的固相率都随凝固时间的增加以二次函数的形式增长，同一时刻纯扩散时多枝晶生长的固相率要大一些，固相率之间的差距随着时间的增长而增大。可见，强迫对流的冲刷作用虽然促进了迎流枝晶的生长，但也抑制了顺流枝晶的生长。同时，强迫对流还使得枝晶间的相互作用更加强烈，这最终导致强迫对流对枝晶生长的促进作用要小于其抑制作用。

图6 纯扩散及强迫对流作用下多枝晶生长的固相率与凝固时间的关系Fig.6 Relationship between solid fraction and solidification time for multiple grains growth without and with flow

4 结论

1) 基于KKS相场模型，建立了一个新的耦合相场、溶质场、流场、取向场和温度场并适应HCP晶系的单相二元合金相场模型，并采用该模型研究纯扩散时和强迫对流作用下的多枝晶生长行为。

2) 纯扩散时，枝晶间未相互碰撞前，枝晶间无相互影响，枝晶呈明显六方异性，与单枝晶生长过程相同。枝晶相互碰撞后，枝晶的生长受到了抑制，枝晶尖端变秃，在碰撞区域出现溶质的富集。

3) 强迫对流作用时，热量和溶质被过冷熔体冲刷到下游，从而加速了枝晶在上游方向的生长，抑制了下游方向的生长，枝晶互相影响并竞争生长，最终形成非对称枝晶形貌。模拟结果与实验结果十分相似。

4) 计算了不同凝固条件下的枝晶尖端生长速度以及纯扩散时和强迫对流作用下多枝晶生长的固相率变化曲线。尖端速度的大小关系为vtip1＞vtip2＞vtip3＞vtip4＞vtip5＞vtip6；同一时刻纯扩散时多枝晶生长的固相率比强迫对流作用下的要大。

5) 该模型能够很好地对不同取向多枝晶的生长进行描述。

[1]SCHUMANN S, FRIEDRICH H.Current and future use of magnesium in the automotive industry[J].Mater Sci Forum,2003, 419/422(1): 51-56.

[2]MORDIKE B L, EBERT T.Magnesium properties-applicationspotential[J].Mater Sci Eng A, 302(1): 37-45.

[3]FRIEDRICH H, SCHUMANN S.Research for a “new age of magnesium” in the automotive industry[J].Journal of Materials Processing Technology, 2001, 117(3): 276-281.

[4]EIKEN J, BÖTTGER B, STEINBACH I.Phase field simulations of microstructure evolution during solidification of magnesium-based alloys[C]// Modeling of Casting, Welding and Advanced Solidification Processes-XI, TMS, 2006: 489-493.

[5]EIKEN J.Dendritic growth texture evolution in magnesiumbased alloys investigated by phase-field simulation[J].International Journal of Cast Metals Research, 2009, 22(1/4):86-89.

[6]BÖTTGER B, EIKEN J, STEINBACH I.Phase field simulation of equiaxed solidification in technical alloys[J].Acta Mater,2006, 54(10): 2697-2704.

[7]WANG M Y, WILLIAMS J J, JIANG L, CARLO F DE, JING T,CHAWLA N.Dendritic morphology ofα-Mg during the solidification of Mg-based alloys: 3D experimental characterization by X-ray synchrotron tomography and phase-field simulations[J].Scripta Materialia, 2011, 65(10):855-858.

[8]WANG M Y, JING T, LIU B C.Phase-field simulations of dendrite morphologies and selected evolution of primaryα-Mg phases during the solidification of Mg-rich Mg-Al-based alloys[J].Scripta Materialia, 2009, 61(8): 777-780.

[9]MONTIEL D, LIU L, XIAO L, ZHOU Y, PRIVATAS N.Microstructure analysis of AZ31 magnesium alloy welds using phase-field models[J].Acta Mater, 2012, 60(16): 5925-5932.

[10]缪家明, 荆 涛, 柳百成.镁合金枝晶形貌的相场方法模拟[J].金属学报, 2008, 44(4): 483-488.MIAO Jia-ming, JING Tao, LIU Bai-chang.Numerical simulation of dendritic morphology of magnesium alloys using phase field method[J].Acta Metallurgica Sinica, 2008, 44(4):483-488.

[11]袁训锋, 丁雨田, 郭廷彪, 胡 勇.强制对流作用下镁合金枝晶生长的相场法数值模拟[J].中国有色金属学报, 2010, 20(8):1474-1480.YUAN Xun-feng, DING Yu-tian, GUO Tin-biao, HU Yong.Numerical simulation of dendritic growth of magnesium alloys using phase-field method under forced flow[J].The Chinese Journal of Nonferrous Metals, 2010, 20(8): 1474-1480.

[12]WHEELER A A, MURRAY B T, SCHAEFER R J.Computation of dendrites using a phase field model[J].Physica D, 1993,66(1/2): 243-262.

[13]SUZUKIA T, ODE M, KIM S G, KIM W T.Phase-field model of dendritic growth[J].J Cryst Growth, 2002, 237/239(1): 125-131.

[14]KIM S G, KIM W T, SUZUKIA T.Phase-field model for binary alloys[J].Phys Rew E, 1999, 60(6): 7186-7197.

[15]KIM S G, KIM W T, SUZUKIA T.Interfacial compositions of solid and liquid in a phase-field model with finite interface thickness for isothermal solidification in binary alloys[J].Phys Rew E, 1998, 58(3): 3316-332.

[16]KOBAYASHI R, WARREN J A, CARTER W C.A continuum model of grain boundaries[J].Physica D, 2000, 140(1/2):141-150.

[17]付振南, 许庆彦, 熊守美.基于概率捕获模型的元胞自动机方法模拟镁合金枝晶生长过程[J].中国有色金属学报, 2007,17(10): 1567-1573.FU Zhen-nan, XU Qing-yan, XIONG Shou-mei.Numerical simulation on dendrite growth process of Mg alloy using cellular automaton method based on probability capturing model[J].The Chinese Journal of Nonferrous Metals, 2007, 17(10):1567-1573.

[18]MALTAIS A, DUBE D, FISET M, LAROCHE G, TURGEON S.Improvements in the metallography of as-cast AZ91 alloy[J].Materials Characterization, 2004, 52(2): 103-119.