合金定向凝固一次枝晶间距模拟

张显飞, 赵九洲

(1. 中国科学院 金属研究所，沈阳 110016；2. 沈阳理工大学 材料科学与工程学院，沈阳 110159)

合金定向凝固一次枝晶间距模拟

张显飞1,2, 赵九洲1

(1. 中国科学院 金属研究所，沈阳 110016；2. 沈阳理工大学 材料科学与工程学院，沈阳 110159)

建立二元合金树枝晶生长的二维元胞自动机模型，模拟丁二腈−2.5%(质量分数)乙醇定向凝固枝晶生长和一次枝晶间距选择过程。模拟结果表明：在给定的凝固条件下，定向凝固一次枝晶间距可在一个范围内变化，其具体取值与凝固历史具有相关性。在相同的温度梯度和不同冷却速度下，模拟给出的一次枝晶间距上、下限与实验结果吻合较好，详细分析影响定向凝固一次枝晶间距上下限的因素。结果表明：在给定凝固条件和合金系条件下，液相中无对流，影响一次枝晶间距上下限的主要因素是界面能和溶质扩散系数。

合金；定向凝固；枝晶间距；元胞自动机；模拟

定向凝固一次枝晶间距一直是凝固理论研究的一个重要课题。许多研究结果表明定向凝固一次枝晶间距与凝固条件存在单值对应关系，即在一定的生长条件下，一次枝晶间距λ1是一个定值，λ1与凝固速度v和凝固界面前沿温度梯度G间满足函数关系λ1∝v-aG-b[1−9]。然而，一些定向凝固实验却表明，一次枝晶间距与稳态凝固时的凝固条件并非一一对应，而是可以在一定范围内变化，具体取值与枝晶达到稳态生长的过程有关，即一次枝晶间距具有历史相关性[10−13]。WARREN和LANGER[14]以及HUNT和LU等[15]分别分析了枝晶列的稳定性，分析结果也表明稳态一次枝晶间距存在一个范围。HUNT和LU等[15]根据枝晶间溶质流的方向确定了定向凝固一次枝晶间距的下限，上限取为下限的两倍。

近年来，树枝晶生长的数值模型发展很快，元胞自动机(CA)方法是广泛应用的数值模型之一。RAPPAZ和GANDIN[16]最早用CA方法研究了等温场内凝固组织形成过程。GANDIN和RAPPAZ[17]将元胞自动机模型与有限元方法相耦合，建立了CA-FE模型，实现了对二维非等温度场内凝固组织形成过程的模拟。SPITTLE和BROWN[18]将元胞自动机与有限差分方法相耦合，建立了CA-FD模型，模拟研究了柱状晶生长过程。NASTAC[19]耦合了温度场、浓度场计算，用界面溶质守恒方法计算固/液界面生长速度，模拟了单个枝晶和小型定向凝固组织。ZHU等[20]发展了MCA模型，计算了固相和液相的浓度场，考虑了曲率过冷和界面溶质再分配，模拟了等轴晶、定向凝固柱状晶组织。元胞自动机模型可以很好地模拟枝晶的分枝结构，可用来模拟定向凝固一次枝晶间距选择。WANG等[21]模拟了镍基单晶高温合金的枝晶生长，考虑了成分过冷和曲率过冷，成功模拟了定向凝固一次枝晶间距的上下限形成过程。单博炜等[22]模拟了丁二腈−2.5%(质量分数)乙醇合金定向凝固一次枝晶间距的上下限，在处理一次枝晶间距选择范围的问题时关注更具物理意义的单个枝晶间距的选择行为，通过对模拟结果的拟合得到了定向凝固一次枝晶间距的上下限，模拟结果与实验结果吻合较好。但是没有考虑界面能的各向异性。

本文作者应用元胞自动机模型模拟了丁二腈−2.5%(质量分数)乙醇定向凝固一次枝晶间距选择过程，分析了影响定向凝固一次枝晶间距范围的因素。

1 模型及数值算法

假设液相无对流，溶质传输由扩撒控制，液相溶质浓度场控制方程为

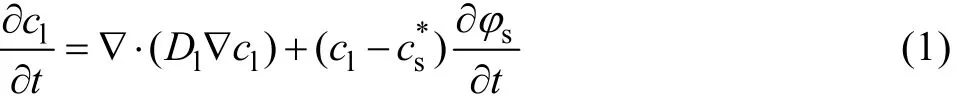
式中：cl为液相溶质浓度；t为时间；Dl为液相溶质扩散系数；为固/液界面固相溶质浓度；φs为界面元胞固相分数。式中右边第二项表示因固/液界面推进而排出的溶质量。

假设固/液界面处于平衡态，固/液界面液相溶质浓度和固相溶质浓度为

式中：c0为初始液相溶质浓度；T*为固/液界面温度；Teq为初始熔体平衡液相线温度；ml为平衡液相线斜率，假定为常数；Γ为Gibbs–Thomson系数；k0为平衡溶质分配系数；θ为择优生长方向与x轴的夹角；φ为界面法向与x轴的夹角[23]，如图1所示；f(φ,θ)为各向异性函数[24]；ε为界面能各向异性强度；为固/液界面平均曲率[25]；∆s为元胞尺寸；N为邻近元胞数，取近邻和次近邻作为邻近元胞，N=8；φsk为邻近元胞固相分数；k为第k个邻近元胞。

根据固/液界面处溶质守恒关系计算界面法向生长速度vn[23]。

固/液界面元胞固相分数可用下式计算：

式中：S为固/液界面沿法向方向在界面元胞内扫过的面积，如图1所示；Scell为界面元胞的总面积。

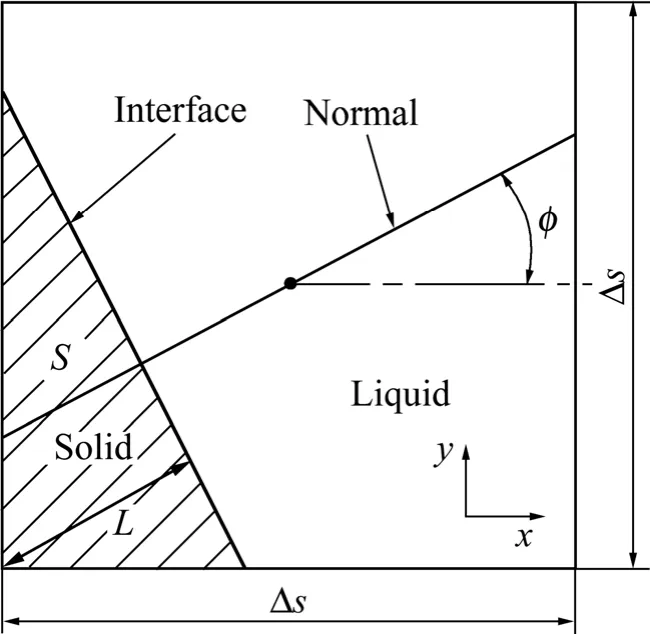
图1 固/液界面元胞固相分数算法示意图Fig. 1 Schematic diagram of algorithm for solid fraction of interfacial cell

2 结果及讨论

2.1 一次枝晶间距的历史相关性

对丁二腈−2.5%乙醇的凝固过程进行了模拟研究。丁二腈−2.5%乙醇的热物性参数见表1。模拟针对HUANG等[10]所用的定向凝固实验条件：凝固界面前沿熔体的温度梯度G=10.8 K/mm、冷却速率为0.54 K/s(对应的稳态凝固速度为v=50 μm/s)。模拟区域宽度(垂直于凝固方向)为3 mm。模拟考察了不同初始枝晶数目(n)条件下定向凝固组织演变过程，结果示于图2。可见，当n≤13时，在两个初始一次枝晶间均形成新的一次枝晶，稳态生长时的一次枝晶间距小于初始一次枝晶间距；当33≥n≥14时，在初始的一次枝晶间没有新的一次枝晶形成，稳态生长时的一次枝晶间距与初始一次枝晶间距相同；当n≥34时，初始一次枝晶发生间湮没现象，稳态生长时的一次枝晶间距大于初始一次枝晶间距。这些结果表明，在给定的凝固条件下，稳态生长一次枝晶间距与初始一次枝晶间距(取决于初始形核过程，具有一定的随机性)有关，可在一定范围内变化(见图3)，即一次枝晶间距与初始一次间距不具备一一对应关系。这一现象可如下解释：当两个一次枝晶的间距过大时，通常通过分枝的机制对间距进行调整。两个一次枝晶间能否形成新的一次枝晶取决于两方面因素：1)固/液界面的稳定性；2)一次枝晶间液相成分过冷情况。这两个方面均与两个原始枝晶的间距有关。图4所示为两个一次枝晶间的凝固界面能否失稳并成长成一个新的枝晶与两个原始枝晶间距之间的关系。当两个枝晶间间距较小时(λ12)，两个一次枝晶周围的溶质浓度场相互叠加，枝晶间液相沿凝固方向的溶质浓度梯度较小，不足以在两个一次枝晶间的液相内造成成分过冷区，因此，界面保持稳定，没有新枝晶的形成；当两个枝晶间间距增加至λ23时，两个一次枝晶周围的溶质浓度场交叠程度下降，枝晶间液相沿凝固方向的溶质浓度梯度增加，一次枝晶间液相内出现了成分过冷区，因此，界面失稳，形成凸起，但在凸起长大过程中，凸起尖端排出的溶质向外扩散困难，造成在凸起尖端处液相出现较高的溶质富集，使凸起尖端过冷度趋向于0，凸起不能继续长大形成一次枝晶；当两个枝晶间间距增加至λ34时，两个一次枝晶周围的溶质浓度场交叠程度大幅度下降，甚至没有交叠，枝晶间液相沿凝固方向的溶质浓度梯度和成分过冷区进一步增加，界面失稳，形成凸起，并且在凸起长大过程中，排出的溶质能顺畅地向远处扩散传输，凸起逐渐长成一次枝晶。由此可见，在给定凝固条件下，存在着一个临界的一次枝晶间距，当两个枝晶间的间距大于临界枝晶间距时，枝晶间可以形成新的一次枝晶，使枝晶间距减小；当两个枝晶间的间距小于临界枝晶间距(即枝晶间距在λ12～λ34之间)时，枝晶间不能生成形成新的一次枝晶，即一次枝晶间距可在一定范围内变化，具体取值与凝固时枝晶形成的历史有关。

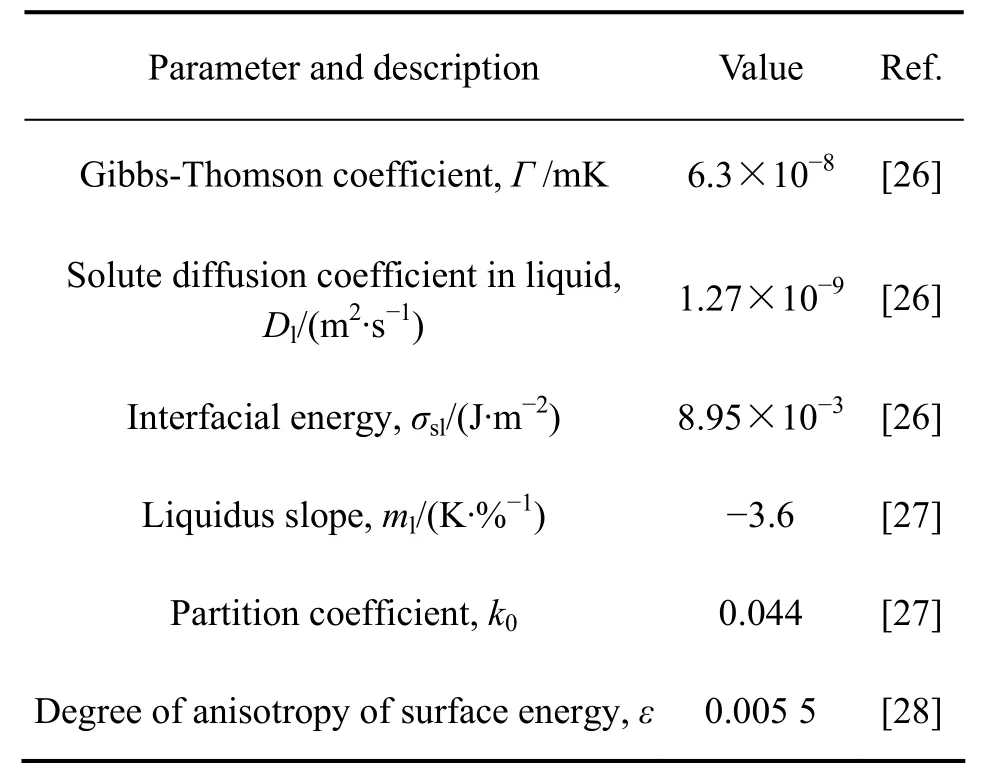
表1 丁二腈−乙醇的热物性参数Table 1 Thermophysical properties of succinonitrile-2.5% ethanol

图2 不同初始枝晶条件下丁二腈−2.5%乙醇定向凝固达到稳态时的枝晶列Fig. 2 Steady state dendrite arrays in directionally solidified succinonitrile-2.5% ethanol sample with different initial dendrite seeds number (n) (Temperature gradient in front of solidification interface is 10.8 K/mm. Sample were solidified at rate of 50 μm/s): (a)n=8; (b)n=13; (c)n=14; (d)n=25; (e)n=33; (f)n=34)

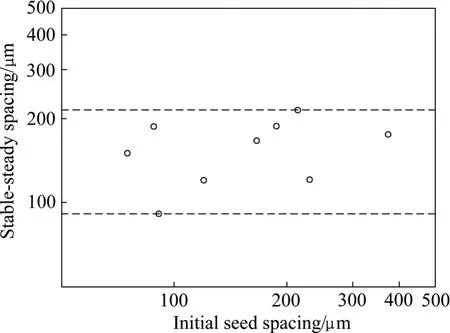
图3 稳态生长时的一次枝晶间距与初始一次枝晶间距的关系Fig. 3 Relationship between stable-steady spacing and initial dendrite spacing

图4 不同一次枝晶间距条件下枝晶间熔体的成分过冷及新枝晶的形成过程示意图Fig. 4 Schematic diagrams of constitutional undercooling of liquid between two dendrites of different spacing and possibility to form new dendrite between two original dendrites (Dash-dot lines are temperature profile, solid lines indicate liquidus temperature, dashed lines are concentration of liquid, cross hatched region is constitutional undercooling zone,t1＜t2＜t3)

由上述分析可知，凡是影响固/液界面稳定性和浓度场的因素，均会影响一次枝晶间距的上、下限。对于给定的合金和凝固条件，在没有对流的条件下，影响一次枝晶间距上、下限的因素主要有溶质扩散系数和固/液界面能。溶质扩散系数越小，一个枝晶周围的溶质浓度场梯度越高、影响范围越小，两个相邻枝晶周围的浓度场只有在较小的枝晶间距条件下才能发生交叠，因此，一次枝晶间距上、下限越小。由固/液界面稳定性的动力学理论可知[29]，固/液界面能有利于固/液界面的稳定，即随着固/液界面能的增加，界面失稳的临界过冷度增加。由此可以推断，在其它条件都不变时，随着固/液界面能的增加，枝晶间距的上、下限增大。

为了证明以上分析，通过假定不同的固/液界面能,模拟计算了定向凝固二腈−2.5%乙醇一次枝晶间距的上、下限随固/液界面能的变化关系，结果示于图5。由图5可见，枝晶间距的上、下限随着固/液界面能的增加而增大。

图5 温度梯度为10.8 K/mm和凝固速度为50 μm/s时定向凝固二腈−2.5%乙醇试样中一次枝晶间距上、下限随固/液界面能(σsl)的变化关系Fig. 5 Variation of simulated upper (λmax) and lower (λmin) limits of primary dendrite spacing in directionally solidified succinonitrile-2.5% ethanol sample with solid/liquid interface energy (Temperature gradient in front of solidification interface is 10.8 K/mm, samples were solidified at rate of 50 μm/s)

2.2 一次枝晶间距的上、下限与凝固速度间关系

上述分析表明，在给定的凝固条件下，存在一个最大临界间距λmax或最小临界枝晶密度nmin(单位长度内一次枝晶的数目，λmax=1/(nmin−1))，当n=nmin时，会有新的一次枝晶生成；n=nmin+1时，没有新的一次枝晶形成，则一次枝晶间距上限λmax应满足：1/nmin＜λmax＜1/(nmin−1)。同样，在给定的凝固条件下，存在一个最小临界间距λmin或最大临界枝晶密度nmax，当n=nmax时，一次枝晶稳定生长，没有一次枝晶湮没现象；当n=nmax+1时，发生一次枝晶湮没现象，则一次枝晶间距下限λmin应满足：1/nmin＜λmin＜1/(nmin−1)。据此，在模拟计算中，可以通过逐渐增加一次枝晶的密度来确定给定凝固条件下一次枝晶间距的上、下限。

针对HUANG等[10]的定向凝固实验条件，模拟计算了丁二腈−乙醇定向凝固一次枝晶间距上、下限与凝固速度间的关系，模拟结果示于图6。可见模拟结果与实验结果吻合得很好。通常一次枝晶间距与凝固速度间的关系可用幂函数表示：λmax=av-b，λmin=a′v-b′[10]。将模拟结果进一步整理，对丁二腈−2.5%乙醇，温度梯度为10.8 K/mm时，定向凝固一次枝晶间距上、下限与凝固速度间满足：

HUANG等[10]的实验表明，b=0.430，b′=0.254，可见本研究的模拟结果与实验结果十分接近，上限与实验结果的吻合程度要优于单博炜等的模拟结果。

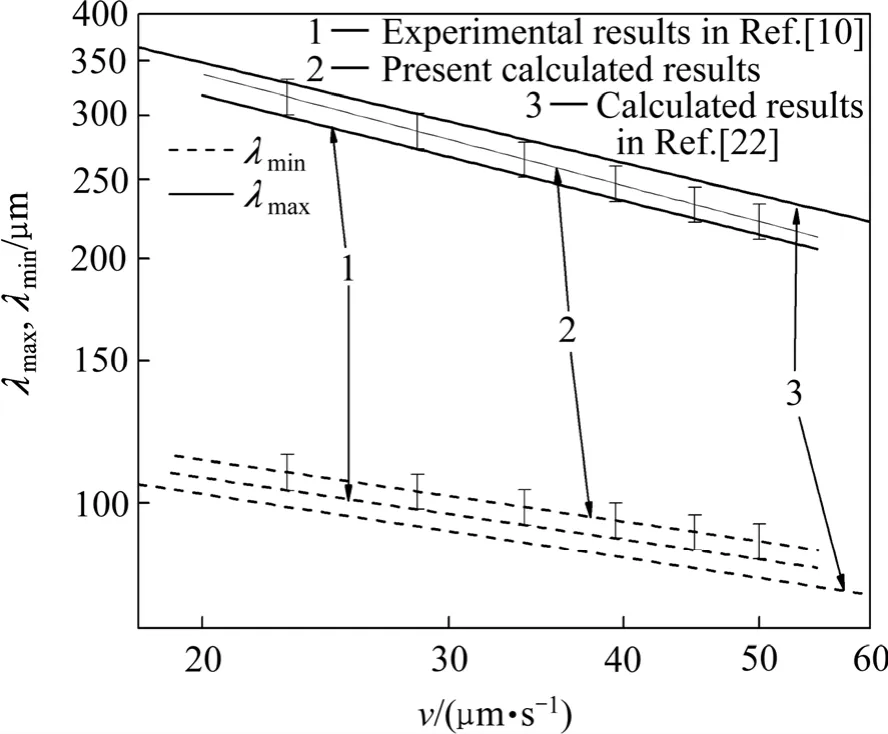
图6 定向凝固丁二腈−2.5%乙醇试样中一次枝晶间距上、下限与凝固速度间关系Fig. 6 Relationship between upper and lower limits of primary dendrite spacing in directionally solidified succinonitrile-2.5% ethanol sample and solidification rate (Temperature gradient in front of solidification interface is 10.8 K/mm)

3 结论

1) 用元胞自动机方法模拟了丁二腈−2.5%乙醇合金定向凝固组织形成过程。结果表明：在给定凝固条件下，一次枝晶间距可在一定范围内变化，即稳态凝固一次枝晶间距与凝固历史具有相关性。

2) 凡是影响固/液界面稳定性和浓度场的因素，均影响一次枝晶间距的上、下限。对于给定合金和凝固条件，在没有对流的条件下，影响一次枝晶间距上、下限的因素主要为溶质扩散系数和固/液界面能。

REFERENCES

[1]HUNT J D. Solidification and casting of metals[M]. London: The Metal Society, 1979: 3.

[2]KURZ W, FISHER D J. Dendrite growth at the limit of stability: tip radius and spacing[J]. Acta Metallurgica, 1981, 29: 11−20.

[3]TRIVEDI R. Interdendritic spacing: Part Ⅱ. A comparison of theory and experiment[J]. Metallurgical Transactions A, 1984, 15(6): 977−982.

[4]KAYA H, ÇADIRLI E, KESLIOGLU K, MARAŞLI N. Dependency of the dendritic arm spacings and tip radius on the growth rate and composition in the directionally solidified succinonitrile-carbon tetra bromide alloys[J]. Journal of Crystal Growth, 2005, 276: 583−593.

[5]GÜNDÜZ M, ÇADIRLI E. Directional solidification of aluminium-copper alloys[J]. Materials Science and Engineering A, 2002, 327: 167−185.

[6]QU M, LIU L, TANG F T, ZHANG J, FU H Z. Effect of sample diameter on primary dendrite spacing of directionally solidified Al-4%Cu alloy[J]. Transactions of Nonferrous Metals Society of China, 2009, 19(1): 1−8.

[7]HU X W, LI S M, CHEN W J, GAO S F, LIU L, FU H Z. Primary dendrite arm spacing during unidirectional solidification of Pb-Bi peritectic alloys[J]. Journal of Alloys and Compounds, 2006, 484: 631−636.

[8]司乃潮, 许能俊, 司松海, 李达云, 史 剑. 温度梯度对定向凝固Al-4.5%Cu合金一次枝晶间距的影响[J]. 材料工程，2011(4): 75−79. SI Nai-chao, XU Neng-jun, SI Song-hai, LI Da-yun, SHI Jian. Effect of temperature gradient on primary dendrite spacing during directional solidification of Al-4.5%Cu Alloy[J]. Journal of Materials Engineering, 2011(4): 75−79.

[9]司乃潮, 史 剑, 司松海, 李达云, 许能俊. 晶体生长速率对定向凝固Al-4.5%Cu合金一次枝晶间距的影响[J]. 铸造, 2010, 59(11): 1172−1177. SI Nai-chao, SHI Jian, SI Song-Hai, LI Da-yun, XU Neng-jun. Effect of crystal growth rate on primary dendritic spacing for Al-4.5%Cu alloy during directional solidification[J]. Foundry, 2010, 59(11): 1172−1177.

[10]HUANG W D, GENG X G, ZHOU Y H. Primary spacing selection of constrained dendritic growth[J]. Journal of Crystal Growth, 1993, 134: 105−115.

[11]LIN X, HUANG W, FENG J, LI T, ZHOU Y. History-dependent selection of primary cellular/dendritic spacing during unidirectional solidification in aluminium alloys[J]. Acta Materialia, 1999, 47(11): 3271−3280.

[12]丁国陆, 林 鑫, 黄卫东, 周尧和. 定向凝固一次枝晶的历史相关性[J]. 金属学报, 1995, 31(10): 469−474. DING Guo-lu, LIN Xin, HUANG Wei-dong, ZHOU Yao-he. History dependence of primary dendritic spacing during unidirectional solidification[J]. Acta Metallurgica Sinica, 1995, 31(10): 469−474.

[13]ÜSTÜN E, ÇADIRLI E, KAYA H. Dendritic solidification and characterization of a succinonitrile-acetone alloy[J]. Journal of Physics: Condensed Matter, 2006, 18: 7825−7839.

[14]WARREN J A, LANGER J S. Prediction of dendritic spacings in a directional-solidification experiment[J]. Physical Review E, 1993, 47(4): 2702−2712.

[15]HUNT J D, LU S Z. Numerical modeling of cellular/dendritic array growth: spacing and structure predictions[J]. Metallurgical and Materials Transactions A, 1996, 27: 611−623.

[16]RAPPAZ M, GANDIN C H A. Probabilistic modelling of microstructure formation in solidification processes[J]. Acta Metallurgica et Materialia, 1993, 41(2): 345−360.

[17]GANDIN Ch A, RAPPAZ M. A coupled finite element-cellular automaton model for the prediction of dendritic grain structures in solidification processes[J]. Acta Materialia, 1994, 42(7): 2233−2246.

[18]SPITTLE A, BROWN S G R. A cellular automaton model of steady-state columnar-dendritic growth in binary alloys[J]. Journal of Materials Science, 1995, 30: 3989−3994.

[19]NASTAC L. Numerical modeling of solidificaiton morphologies and segregation patterns in cast dendritic alloys[J]. Acta Materialia, 1999, 47(17): 4253−4262.

[20]ZHU M F, CAO W, CHEN S L, HONG C P, CHANG Y A. Modeling of microstructure and microsegregation in solidification of multi-component alloys[J]. Journal of Phase Equilibria and Diffusion, 2007, 289(1): 130−138.

[21]WANG W, LEE P D, MCLEAN M. A model of solidification microstructures in nickel-based superalloys: predicting primary dendrite spacing selection[J]. Acta Materialia, 2003, 51(10): 2971−2987.

[22]单博炜, 黄卫东, 林 鑫, 魏 雷. 元胞自动机模型模拟枝晶一次间距的选择[J]. 金属学报, 2008, 44(9): 1042−1050. SHAN Bo-wei, HUANG Wei-dong, LIN Xin,WEI Lei. Dendrite primary spacing selection simulation by the cellular automaton model[J]. Acta Metallurgica Sinica, 2008, 44(9): 1042−1050.

[23]LAZARO B S, STEFANESCU D M. A quantitative dendrite growth model and analysis of stability concepts[J]. Metallurgical and Materials Transactions A, 2004, 35: 2471−2485.

[24]DANTZIG J A, RAPPAZ M. Solidification[M]. Lausanne: EPFL Press, 2009: 290.

[25]SASIKUMAR R, SREENIVASAN R. Two dimensional simulation of dendrite morphology[J]. Acta Metallurgica et Materialia, 1994, 42: 2381−2386.

[26]GLICKSMAN M E, SCHAEFER R J, AYERS J D. Dendritic growth-a test of theory[J]. Metallurgical Transactions A, 1976, 7(11): 1747−1759.

[27]SCHAEFER R J, CORIELL S R. Convection-induced distortion of a solid-liquid interface[J]. Metallurgical Transactions A, 1984, 15(10): 2109−2115.

[28]CHEN Z, CHENG C L, HAO L M. Numerical simulation for isothermal dendritic growth of succinonitrile-acetone alloy[J]. Transactions of Nonferrous Metals Society of China, 2008, 18: 654−659.

[29]KURZ W, FISHER D J. 凝固原理[M]. 包协民, 包冠乾, 译.西安: 西北工业大学出版社, 1987: 190. KURZ W, FISHER D J. Fundamentals of solidification[M]. BAO Xie-min, BAO Guan-qian, transl. Xi’an: Northwestern Polytechnical University Press, 1987: 190.

(编辑 李艳红)

Simulation of primary dendrite spacing in unidirectionally solidified alloy

ZHANG Xian-fei1,2, ZHAO Jiu-zhou1
(1. Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China；2. School of Materials Science and Engineering, Shenyang Ligong University, Shenyang 110159, China)

A two-dimensional cellular automaton model for simulation of dendritic growth during solidification of binary alloy was built. The microstructural evolution in a directionally solidified succinonitile-2.5% (mass fraction) ethanol alloy was simulated. The results show that the primary dendrite spacing may vary in a range under a given solidification condition. Its value depends on the solidification history of the sample. The calculated upper and lower limits of primary dendrite spacing at different cooling rates are in good agreement with the experimental results. The effect factors of the solidification history dependence of the primary dendritic spacing were analyzed in detail. It indicates that the interfacial energy and the solute diffusion coefficients are the main factors if there is no convection in the liquid phase.

alloy; directional solidification; primary dendrite spacing; cellular automaton; simulation

TG111.4

A

国家自然科学基金资助项目(51071159, 51031003, u0837601)

2011-09-07；

2011-12-27

赵九洲，研究员，博士；电话：024-23971918；E-mail: jzzhao@imr.ac.cn

1004-0609(2012)10-2868-07