气动外形优化中的分块类别形状函数法研究
2014-12-15刘传振段焰辉蔡晋生
刘传振,段焰辉,蔡晋生
(西北工业大学航空学院,西安710072)
0 引言
飞行器几何外形的参数化方法在气动外形优化设计中有非常重要的作用,参数化方法的性质对计算时间和设计空间的本质特性与范围有十分深刻的影响,进而大大影响了气动外形优化的效率。适用于飞行器外形优化的参数化方法应该具有以下性质[1]:(1)生成光滑可行的几何形状;(2)具有高效性和鲁棒性;(3)计算快速、精确、稳定;(4)使用少量参数表达较大的设计空间;(5)允许某些影响性较大的参数存在;(6)容易控制曲线曲面;(7)表达几何形状直观。
常用的参数化方法[2]在表达复杂曲面时,为保证表达精度,参数的个数会大量增加[3],优化过程中参数变量的随意变化还会导致不规则或不可控外形的产生,影响优化设计的正常实现。Kulfan等提出了一种使用类别函数(class function)和形状函数(shape function)表示几何外形的类别形状函数法(Class and Shape Transformation,CST)[4],CST 方法设计变量少,具有良好的可控性和表达精度,是一种简洁高效的参数化方法。近年来,CST方法在很多方面得到了应用,包括超临界翼型设计[5]、机翼减阻优化[6]、增升装置的表达[7]等,相关学者还实现了飞翼布局[8]和乘波体机身[9]的CST参数化表示,并对其进行了B样条修正[10]。这些工作主要是对翼型、机翼或简单飞行器的外形表达,很少涉及复杂飞行器外形的表达,难以实现复杂气动外形的统一参数化建模。
为了扩展CST方法对飞行器外形曲面的表达能力,本文提出分块CST方法,实现复杂曲面分块的光滑连接,完成飞行器的全机参数化建模。并结合遗传算法[11]和气动力快速计算方法[12-13],以某类乘波翼身组合体飞行器为例验证它在高超声速[14]气动外形优化设计中的作用。
1 分块类别形状函数变换法
1. 1 CST方法的基本原理
本文以翼型为例,说明CST方法的基本原理。对于一般的翼型,其几何外形可由CST方法表示为:

其中ζ=z/c为翼型无量纲z坐标,ψ=x/c为翼型的无量纲x坐标,ζR为无量纲后缘厚度,c为翼型弦长。类别函数(ψ)定义为:
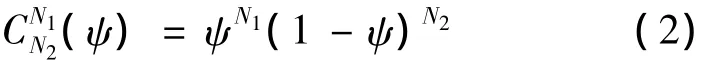
其中,N1和N2定义了几何外形的类别[4]。
形状函数S(ψ)有多种方法定义,本文采用n阶Bernstein多项式的加权组合作为S(ψ)的表达形式,如式(3):

对于任意平面形状的曲面进行CST参数化建模,可以通过坐标变换将曲面块在x-y平面的两个方向进行单位化处理,采用Bernstein多项式对曲面块进行描述,同时在曲面块的特征方向上增加类别函数,得到曲面块的CST方法表示形式为:

其中ψ为无量纲的x坐标,η为无量纲的y坐标,ζ为无量纲的曲面z坐标。为类型函数,当特征方向选取x或y时,类型函数分别为(ψ)或(η)。和(η)为两方向的Bernstein多项式函数,bi,j是曲面控制参数。坐标变换的表达式为:

其中xR,xL为曲面块在x-y平面上x方向的边界,yU,yD为曲面块在x-y平面上y方向的边界。坐标变换(5)将曲面块在x-y平面的自变量区域变为ψη平面上的单位正方形区域。当特征方向沿y方向时,在式(4)中的ζ与曲面块z坐标的变换关系为:

其中zU与zD分别是曲面块位于yU与yD边界处轮廓线的z坐标。轮廓线是一条三维曲线,可以采用二维CST方法分别表示轮廓线在x-y和x-z平面的投影为:

其中ϑL与ϑR以及ζL与ζR分别为轮廓线起点与终点偏离原点的位置。
1. 2 分块处理及曲面接合方法
飞行器的外形复杂,机翼机身很难用一整块曲面表示,即使同一曲面的性质和复杂程度在不同区域也不同,因此采用分块处理是十分重要和必要的。本文根据气动力和几何形状的不同性质将飞行器曲面划分为不同的区域,每个曲面块区域分别采用CST方法进行参数化描述,组合所有曲面块形成一个完整的飞行器曲面。
在分块单独采用CST方法进行描述时,很难在相邻块边界保证相接曲面块的连续和光滑,因此需要增加相应的约束来保证曲面块在交接处的连续光滑性。本文分析CST曲面在边界处取值和导数的特性,推导CST曲面在边界处取值和导数值与特定参数的关系,给出了保证相邻曲面块连续光滑的参数约束条件。
由n阶Bernstein多项式(3)推导导数公式为:

以特征方向为ψ方向为例,考虑η方向的边界连续条件。边界处η=0和η=1,此时方程(4)简化为:

只要控制bi,j的首行参数即可保证η=0处的边界条件,控制末行参数可保证η=1处的边界条件。
下面讨论CST曲面在边界处的导数连续条件。CST曲面在η方向的导数是

当η=0时,

曲面导数公式简化为

当η=1时,
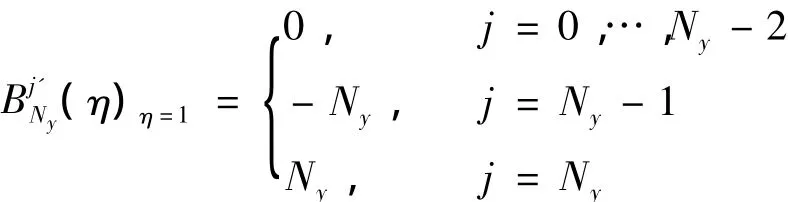
曲面导数公式简化为

由此可以看到bi,j两端的两行系数决定了边界处的导数值。连续性条件已确定首行或末行的系数,因此仅需要调整第二行或倒数第二行的参数即可满足导数连续条件。
2 分块CST方法特性分析
本文以两类曲面外形为例研究了分块CST方法的性质:一类曲面特性相同,但复杂度不同,研究表明采用分块处理可以有效保证精度并减少参数;另一类曲面特性不同,难以进行统一单块处理,分块CST方法则可以较好地表达,说明其适用性。
2. 1 复杂度不同曲面的分块建模
对于如图1所示的外形,在曲面的不同区域其复杂程度不同,前段曲面曲率变化大,而后段较平缓。对于此类型的曲面,分块处理可以有效保证精度并减少参数数目。下面比较采用分块CST表达和统一表达的精度。

图1 某类乘波体下表面机身Fig.1 Lower surface of quasi-waverider
横截面方向为CST方法的特征方向,称为弦向,另一方向为展向。本文采用最速下降法这一优化算法计算控制参数,拟合几何体与原几何体的残差作为目标函数:
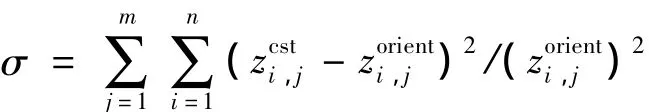
经测试,分块时前后段曲面在弦向和展向分别选择6×5和4×3阶多项式可较好的表达,考虑曲面对称性,参数数目为33,残差σ为0.898 7;统一处理时,残差σ随阶数的变化如表1。
从表1看到如果要达到相同精度的误差,阶数应至少选择为6×8阶,参数有36个,比分块处理所用参数多。这是因为后段曲面较简单,使用低阶多项式即可较好的表达。分块CST方法处理此类型曲面时具有一定优势。

表1 统一CST表达时残差σ随阶数的变化Table 1 Residuals of uniform CST method via orders
2. 2 形状特性不同曲面的分块建模
对于类别形状差异较大的曲面比如机翼机身或不同形状性质的机翼曲面,CST方法难以统一处理,而分块CST方法则可较好表达。下面以高速运输飞行器(High Speed Civil Transport,HSCT)的机翼[1]为例说明分块CST方法的适用性。

图2 HSCT飞行器的机翼Fig.2 Wing of HSCT
对于图2所示的机翼,内翼为亚声速钝前缘翼型,外翼为超声速尖前缘翼型,在使用CST方法表达时,内外翼应使用不同的类型函数。针对不同翼面的物理和气动特性,将机翼分为内外上下四个曲面块,分别使用CST方法进行建模,并在交接处应用1.2部分的接合方法对内翼曲面控制参数施加约束保证连续光滑。建模结果如图2,机翼截面在交接处过渡连续光滑,实现了此机翼的整体参数化建模。
3 类乘波翼身组合体优化设计
3. 1 类乘波翼身组合体参数化建模
为了说明分块CST方法在优化设计中的作用,本文以某类乘波翼身组合飞行器为例进行了分块CST方法建模,并对其进行了以升阻特性为目标的优化设计。初始外形如图3,模型来自于美国空军“Falcon”计划[15],该飞行器的机身投影面积明显较机翼面积大很多,机身为主要升力面。对于大多数的高超声速飞行器,都是利用前机身的压缩产生主要升力,因此前机身下表面需要细致设计;机翼作为次要升力部件,具有很大的改善空间,也需重点设计。由初始外形的几何和气动特性确定此飞行器的分块如下:机身前部,机身后部,翼身融合部与机翼,对各部分曲面进行上下分割,整个飞行器外形曲面分为8个曲面块。

图3 类乘波翼身组合体飞行器三视图(无垂尾)Fig.3 Views of the quasi-waverider vehicle
机身前部和后部曲面的建模结果如图4,曲面按照1.2节的接合方法对前后部机身曲面的控制参数施加约束,保证机身表面连续光滑,在图4中可以看到截面形状在机身曲面块的交接处光滑连续。

图4 机身曲面融合部分Fig.4 Adjacent area between body blocks
提取相邻机身和机翼曲面的边界,按照前文介绍的接合方法,约束曲面控制参数即可生成翼身融合面。图5中翼身融合面截面形状的变化与相邻曲面一致,保证了交接区域的连续光滑。机翼采用梯形翼,翼型选择为对称双弧翼型,考虑机身后体减阻与发动机尾喷口放置,参照HTV-3x高超声速飞行器[15]采用样条插值生成了尾锥部分。

图5 翼身融合部分Fig.5 Blended wing-body area
翼型选择双弧形,N1=1.0,N2=1.0;机身为双锥形曲面,截面形状在边界处的斜率较小,因此也选取 N1=1.0,N2=1.0。飞行器的平面形状控制参数包括前后机身长度、宽度,轮廓线参数,机翼位置,翼面积,展弦比,梢根比,后掠角等,总共21个;前后机身分别选取6×5和4×4阶Bernstein多项式,机翼使用3×2阶多项式,考虑到相邻曲面的参数约束关系、机身曲面的对称性等,曲面控制参数为72个。
3. 2 优化及气动力计算方法
优化算法为遗传算法,根据文献[16]的研究结果,在基本遗传算法的基础上加入基于排序的适应度分配方法和优选技术,可以提高遗传算法的效率。
气动力计算采用高超声速快速计算方法。目前比较成熟的计算方法有牛顿法,切楔切锥法,激波膨胀波方法等,针对不同的飞行器部件使用不同的算法,可以有效地增加计算精度。本文算例的飞行器外形类似吻切锥乘波翼身组合体,机身侧边有明显的三维流动特性,因此机身的迎风面和背风面使用带攻角的锥方法;机翼较薄,近似为二维流动,采用激波膨胀波方法;粘性力的计算选取基于平面面元的Spading-Chi方法。
3. 3 优化设计及结果
初始外形如图3,优化的设计点状态为马赫数Ma=6.0,高度 H=30km,攻角 α =3°。
目标函数为设计点状态的升阻比f=CL/CD。高超声速飞行器的容积非常重要,本文在优化时限定容积不小于原始容积的70%。实际优化时发现,随着飞行器性能的提高,前体的体积会大幅度减小,为了满足体积约束,后体的体积开始增大,由于使用工程方法很难对底阻进行精确估算,所以会进一步导致后体的厚度增大,很容易产生类似于“圆锥”一样的外形,这是不合理的,因此本文施加厚度约束,要求前后体对接处的厚度d1不能小于后体尾缘处的厚度d2。从气动力角度考虑,设计目标为升阻比,有可能出现升力过小的情况,因此需约束升力系数,指定升力系数的最小值为CLmin。此优化问题可以表示为:

类函数中N1,N2为定值,不参与优化;21个平面形状控制参数和曲面控制参数均作为设计变量,总设计变量的个数为 93个,较文献[3]中的ATLLAS飞行器模型有较大减少。对特定的设计变量比如机身长度,机身宽度,翼面积等设定范围保证外形规则可控。类乘波体飞行器前下表面的形状对气动性能影响最大,其曲面控制设计变量选定为初始值上下浮动80%,其他曲面选定为初始值上下浮动50%。
遗传算法中种群规模1 000个,交叉概率0.6,变异概率0.05,最大进化代数400。在Ubuntu Linux系统下,采用Intel Core i7处理器(主频2.93GHz),内存8GB,优化程序每一步耗时约135s,其中几何体生成程序耗时约30s,气动力计算程序约100s,总耗时为约15h。

表2 优化前后外形的气动力结果对比Table 2 Comparison of aerodynamic results
图6是目标函数随进化代数的变化图,表2为优化前后飞行器升力系数CL,阻力系数CD,升阻比L/D和飞行器容积V的对比,其中CD大幅度减小,升阻比从原外形的2.59提高到优化外形的5.23。飞行器容积从180 750下降到134 580,满足限制要求。
图7和图8分别是优化前后的飞行器外形对比图和优化外形的三视图,优化后外形表面光滑,机身前缘轮廓线较尖锐,机身变薄,长细比增加,机翼面积、展弦比增大,梢根比减小。

图6 目标函数随进化代数的变化Fig.6 Optimal function via generation

图7 初始(左)与最优(右)外形的对比Fig.7 Initial and optimized configurations

图8 优化后飞行器外形三视图Fig.8 Views of optimized configuration
3. 4 CFD 校验计算
为了校验优化结果和气动力快速计算方法的精度,本文对优化前后的外形进行了CFD校验计算。
计算状态为设计点状态,网格采用非结构网格,湍流模型为S-A模型。图9给出优化后外形Y向位置η=21%(机身)处截面的压力系数对比,可以看到机身截面处的压力分布与CFD结果在大体上是一致的,主要在前缘部分计算不够精确,这是因为前缘部分存在总压驻点,工程方法难以捕捉此处的吸力峰值,属于方法本身的局限。

图9 优化外形η=21%处截面的Cp分布Fig.9 Cp distribution atη =21%of optimized configuration
表3为CFD数值计算的气动力结果,与表2相比较可以看到工程算法与精确CFD计算升阻力特性吻合的较好,说明工程算法也具有较高的精度。同时,精确CFD数值计算对于优化前后升阻比气动特性提升的校验,说明了优化设计平台的精度与效率。

表3 CFD计算气动力结果对比Table 3 Comparison of CFD aerodynamic results
4 结论
通过对CST方法特性的分析,本文提出分块CST方法,实现了复杂飞行器曲面的参数化建模,并以类乘波翼身组合飞行器为例校验了其在优化设计中的应用。
参数化建模结果表明,对于形状变化较大的曲面,分块CST方法可以使用较少的参数表达,并具有较高的精度;对于类别形状性质不同的曲面,分块CST方法能保证不同分区曲面之间的光滑连接,实现曲面的整体参数化建模。
气动外形优化算例表明,基于分块CST方法、遗传优化算法和气动力快速计算方法建立的优化平台设计变量少,具有较高的计算效率、优化效果与精度,是高超声速飞行器气动外形优化设计的有力工具。
[1] Brenda M K.Recent extensions and applications of the‘CST’universal parametric geometry representation method[R].AIAA 2007-7709,2007.
[2] Jamshid A S.Survey of shape parameterization techniques for high-fidelity multidisciplinary shape optimization[J].AIAA Journal,2001,39(5):877 -884.
[3] Longo JA,Dittrich R,Nanuti D,et al.Concept study for Mach 6 transport aircraft[R].AIAA 2009 -435,2009.
[4] Brenda M K,John E B.Fundamental parametric geometry representations for aircraft component shapes[R].AIAA 2006 -6948,2006.
[5] Jacob H,William C.A parametric approach to supercritical airfoil design optimization[R].AIAA 2009 -6950,2009.
[6] 关晓辉,李占科,宋笔锋.CST气动外形参数化方法研究[J].航空学报,2012,33(4):625-633.[Guan Xiao-hui,Li Zhan-ke,Song Bi-feng.A study on CST aerodynamic shape parameterization method[J].Acta Aeronautica et Astronautica Sinica,2012,33(4):625 -633.]
[7] Maxim T,Jinhwan P.Subsonic airfoil and flap hybrid optimization using multi-fidelity aerodynamic Analysis[R].AIAA 2012 -5453,2012.
[8] Pier D C,Thomas Z,Bjorn N.CST parameterization for unconventional aircraft design optimization[C]. 27th International Congress of The Aeronautical Sciences, Nice,France,2010.
[9] Li P,Chen WC.‘CST’parametric geometry representations for waveriders[C]. The Proceedings of 2010 Asia-Pacific International Symposium on Aerospace Technology, Xi’an,China,2010.
[10] Michiel H S,JL Tooren,Mark V.Extension to the class-shapetransformation method based on b-splines[J].AIAA Journal,2011,49(4):780-790.
[11] 陈兵,徐旭,蔡国飙.基于遗传算法和空间推进方法的高超声速进气道优化设计研究[J].宇航学报,2006,27(5):1010 -1015.[Chen Bing,Xu Xu,Cai Guo-biao.Optimization design of hypersonic inlets using genetic algorithm based on a parabolized Navier-Stokes flow solver[J]. Journal of Astronautics,2006,27(5):1010 -1015.]
[12] 高清,张卫民,陈英文.新一代超/高超声速带进气道飞行器气动力特性快速计算[J].宇航学报,2008,29(2):494-498.[Gao Qing, Zhang Wei-min, Chen Ying-wen. Rapid calculation of aerodynamic characteristics of new supersonic and hypersonic aircrafts with inlets[J].Journal of Astronautics,2008,29(2):494 -498.]
[13] 李维东,韩汉桥,陈文龙,等.考虑高空粘性干扰效应的乘波体气动性能工程预测方法研究[J].宇航学报,2011,32(6):1217 -1223.[Li Wei-dong,Han Han-qiao,Chen Wenlong,et al.An engineering prediction method for aerodynamic performance of waverider with hypersonic viscous interaction[J].Journal of Astronautics,2011,32(6):1217 -1223.]
[14] 罗世彬,罗文彩,王振国.基于并联协作混合遗传算法的高超声速巡航飞行器一体化优化设计研究[J].宇航学报,2004,25(1):28 - 34.[Luo Shi-bin,Luo Wen-cai,Wang Zhen-guo.Parallel collaborative hybrid genetic algorithm applied to integrated design optimization of hypersonic cruise vehicle[J].Journal of Astronautics,2004,25(1):28 -34.]
[15] Steve H W,Fredrick R.Falcon hypersonic technology overview[R].AIAA 2005-3253,2005.
[16] 王晓鹏.遗传算法及其在气动优化设计中的应用研究[D].西安:西北工业大学航空学院,2000.[Wang Xiao-peng.Researches on genetic algorithm and its application in aerodynamics shape optimization[D].Xi’an:School of Aeronautics,Northwestern Polytechnical University,2000.]
