敏捷机动小卫星姿态的非线性自适应控制及实验研究

谌 颖，楚中毅，徐静怡

(1.北京控制工程研究所，北京100190;2.北京航空航天大学仪器科学与光电工程学院小卫星与深空探测技术研究所，北京100191)

0 引言

随着航天技术的发展，以及飞行任务等对地观测的需求，敏捷机动成为卫星的重要功能之一，如卫星对地成像、对地目标的跟踪及精确指向［1］等功能都要求卫星具有快速机动的能力。低轨敏捷机动小卫星以其对目标的精确跟踪、对地观测范围广、收集信息量大等特点成为科研人员研究的热点之一［2－3］。小卫星要实现敏捷机动的能力需要较大的姿态控制力矩，但是在重量受限的情况下，动量轮和反作用飞轮等所产生的力矩已不能满足小卫星敏捷机动功能的需求，而控制力矩陀螺(Control Moment Gyro，CMG)因其自身小质量就可以获得较大输出力矩的特点成为敏捷小卫星首选的控制执行机构。

另一方面，在轨运行的卫星会受到各种干扰、模型不确定性［4－5］等因素的影响，这会严重影响姿态控制精度，进而影响姿态机动和姿态跟踪性能。近年来，国内外学者采用各种控制方法来解决航天器的姿态控制问题［1－2，4－7］。文献［1 － 2］中应用了PID饱和或经典的PD控制器实现航天器的姿态控制;文献［4－5］以变速控制力矩陀螺(Variable Speed Control Moment Gyroscope，VSCMG)为执行机构，在考虑执行机构模型的基础上设计了自适应控制器，但从仿真结果来看，航天器机动的快速性有待提高;文献［6］和文献［7］分别采用了四元数和改进的罗得里格参数(MRPs)描述航天器的姿态运动，在考虑模型不确定性和外界干扰的情况下设计了模糊前馈控制器、滑模控制器，但在控制器设计过程中均没有考虑执行机构的动力学模型。近年来，国外学者和研究机构在这方面做了大量的理论和仿真实验研究［1－2］，如英国萨瑞大学研制的微小卫星执行机构CMG MK.II为金字塔构型［2］，并以其为平台进行了单轴姿态机动的实验;美国佛罗里达大学使用搭建的SOBEK(Spacecraft Orientation Buoyancy Experimental Kiosk)仿真平台进行了相关实验［8］。但国内在实验研究方面相对较少，其中长春光学精密机械研究所使用单轴气浮台对SGCMGs进行了半物理仿真实验［9］等。

模型参数不确定性以及外界干扰等因素对航天器的姿态控制有着极大的影响，针对这种情况，自适应控制理论具有一定的优势，因此其在航天器姿态控制中的应用成为众多学者研究的重点方向之一。本文针对航天器在运行过程中会受到各种不确定因素的影响，设计了一种具有自适应能力的控制系统，利用自适应控制的“学习”能力，有效利用控制过程中获得的关于不确定性结构的信息，在线估计参数的不确定性，通过设计合适的参数自适应控制律以减小姿态角和姿态角速度跟踪误差，从而削弱系统参数的不确定性和环境干扰力矩对姿态控制的影响，改善航天器姿控系统的性能。为校验该方法的有效性，本文搭建了基于金字塔构型SGCMGs的半物理仿真实验系统，并在考虑模型不确定性、外界环境干扰及执行机构控制力矩受限的情况下进行了半物理仿真实验研究，通过实验校验了本文方法的有效性。

1 基于CMGs的航天器动力学与运动学描述

1. 1 航天器动力学模型

假设航天器为刚体，执行机构由n个单框架控制力矩陀螺(SGCMG)组成，则卫星整体的角动量公式为［8］

式中，As0、At0和 Ag0是 As、At和 Ag的初始值。

式(2)两端分别对时间求导得

令hCMGs表示SGCMGs的整体角动量，则

将式(4)代入式(1)得

式(4)两端分别对时间求导，可得

由动量矩定理得

其中，对于任意向量x=(x1，x2，x3)T，其反对称矩阵

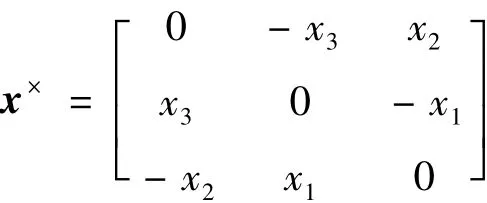
M为航天器运行过程中所受到的外力矩。

式(5)两端分别对时间求导得

不考虑转动惯量随时间变化率的影响，即J·=0，上式化为

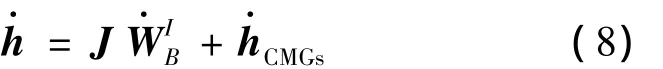
将式(5)和式(8)代入式(7)整理得

假设外力矩M=0，并将式(4)和式(6)代入上式化简后可得

其中，

1. 2 航天器运动学描述

采用修正的罗得里格参数(MRPs)描述航天器姿态运动。

定义 MRPs为 σ，满足下式［10］:

式中^e，φ分别为欧拉旋转主轴的单位矢量和旋转角。σ为3维列向量，且

其中，pi(i=1，2，3，4)为四元数。

用MRPs描述航天器姿态运动方程为:

其中，

I为3×3的单位矩阵。

2 非线性自适应控制器设计

假设

由式(10)可知，用MRPs描述航天器姿态的误差方程为:

由式(13)得

将式(12)和式(14)代入式(9)并左乘G－T(σe)化简得

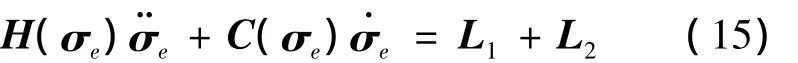
其中，H(σe)=G－T(σe)JG－1(σe);

因为H·(σe)+2C(σe)为斜对称矩阵，所以有

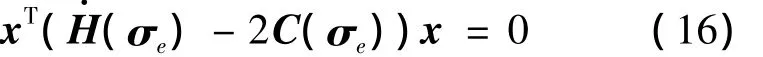
设参数a为6维列向量，且定义如下:

设^a为参数a的估计值，则定义~a=^a－a。

定义一个描述姿态的误差方程［11］

其中，λ是3×3的常值正定矩阵。

预选Lyapunov函数

式中Γ－1为对角阵。

对V求导得

对式(17)两边求导并左乘H(σe)，与式(15)联立可求得

由式(16)，式(17)，式(19)和式(20)联立可求得

定义矩阵［10］

设计控制律为

选取自适应控制律为

将式(22)、式(23)和式(24)代入式(21)整理得

鉴于－sTKps≤0，根据Lyapunov定理可知所设计的控制器是稳定的。

由以上分析可得输出力矩为

在实际应用中，执行机构的输出力矩有一定的限制，考虑控制饱和，设

其中，U为考虑饱和的自适应控制器输出力矩，Umax为饱和力矩。

由式(25)可得

对上式求伪逆得

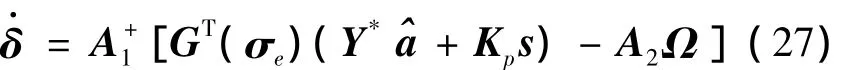
图1 卫星姿态控制的半物理仿真系统图Fig.1 Semi-physical experiment set－ up of the satellite attitude control system

3 半物理仿真实验系统设计与组成

图1所示为搭建的半物理仿真系统图，本文的半物理仿真平台主要由上、下位机两部分组成，上位机主要完成数值仿真的工作，下位机主要实现执行机构的指令运动。金字塔构型的SGCMGs的框架电机采用FAULHABER公司的1524步进电机;转子电机为该公司的1525直流无刷电机;执行机构运动过程中实际的框架角由日本的S-FCPS22R电位计测得;另外，采用Turbo PMAC2实时运动控制板卡实现对框架和转子的伺服控制及上、下位机间的通讯。具体实现过程为:上位机通过数字仿真得到指令框架角速度，并将其发送到下位机，由PMAC卡控制相应的电机驱动SGCMGs按照指令运动，并将实际框架角和转子转速传回上位机进行数字仿真，形成闭环控制系统［12］。

4 半物理仿真实验及结果分析

在搭建的半物理仿真实验平台上对所设计的自适应控制器进行实验校验，其中，金字塔构型的塔面倾角为 β =54.73°，转子的转动惯量为Jω=2.17×10－4kg·m2。假设航天器运行在300km的轨道上，且外界环境干扰力矩均为10－3N·m的常值干扰。则轨道角速度为ω0=0.001 16rad/s。

假设航天器转动惯量的标称值为:

实际转动惯量为:

初始姿态角:φ =0°，θ=0°，ψ =0°;对应的初始罗德里格参数σi=0，初始框架角、框架角速度、姿态角速度均为0。

估计参数的初始值为:

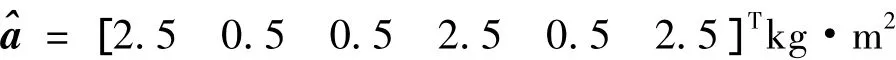
自适应控制器的参数为:

为便于比较还设计了PID控制器，其参数为:

目标姿态为:30s内三轴机动

图2(a)、(b)所示分别为自适应和PID控制器的姿态角误差，在自适应控制方法下，三轴(以下均指横滚轴、俯仰轴和偏航轴)的姿态角误差分别为:0.056°，0.047°，0.034°;PID 控制方法下，三轴的姿态角误差分别为:0.070°，0.050°，0.125°。

图2 姿态角误差Fig.2 The error of the angles

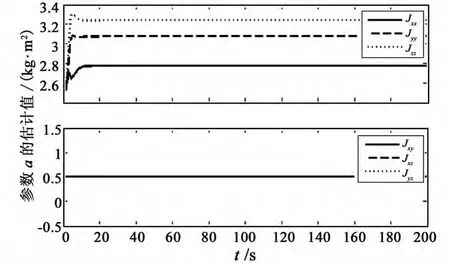
图3 自适应估计参数Fig.3 The estimated parameters of the adaptive method

图4 (a)、(b)所示分别为自适应和PID控制器的姿态角速度跟踪误差，可以看出自适应控制方法的姿态角速度跟踪效果要明显优于PID控制，自适应控制方法下三轴的姿态角速度跟踪误差分别为:0.000 3(°)/s，0.000 3(°)/s，0.000 4(°)/s;PID 控制方法下，三轴的姿态角速度跟踪误差分别为:0.003(°)/s，0.002(°)/s，0.005(°)/s。两种控制方法的姿态角误差和姿态角速度跟踪误差详见表1。图3给出了参数a的估计结果:

图4 姿态角速度误差Fig.4 The error of the angular velocities

图5 实际转子转速Fig.5 The real rotor velocities

图5 为测得的转子实际转速，实际运转过程中转子转速存在近似周期性的波动，经过滤波和PID控制之后，误差控制在4rad/s以内。

表1 两种控制方法的结果对比Table 1 Comparison of the two control methods

图6(a)、(b)所示分别为自适应和PID控制器的指令力矩，图7(a)、(b)和图8(a)、(b)分别对应自适应和PID控制器测得的实际框架角速度和实际框架角。从中可以看出，完成同样的姿态机动、姿态角速度跟踪及克服干扰，自适应控制方法所需能量较少。

图6 指令力矩Fig.6 The control torques

5 结论

图7 框架角速度Fig.7 The gimbal angular velocities

图8 框架角Fig.8 The gimbal angles

针对敏捷小卫星在运行过程中遇到的各种不确定性和干扰等问题，本文研究了一种非线性自适应姿态控制方法，并以单框架控制力矩陀螺为执行机构进行了半物理仿真实验校验。本文控制方法可有效地补偿模型参数不确定性和外界扰动对姿态控制精度和姿态角速度跟踪的影响，尤其在姿态角速度跟踪及能量消耗方面有明显优势，为敏捷卫星的快速机动、快速稳定控制提供了一种可行的参考方案。

［1］ Reimer B.Control moment gyro actuator for small satellite applications［D］.South Africa:University of Stellenbosch，2005.

［2］ Vaios JL.A control moment gyro(CMG)based attitude control system(ACS)for agile small satellite［D］.UK:University of Surrey，2002.

［3］ Argan A，Tavani M，Giuliani A，et al.The data handling system for the AGILE satellite［C］.IEEE Nuclear Science Symposium Conference Record，Rome，Italy，2004.

［4］ 张军，徐世杰.采用VSCMG的航天器IPACS设计的一种投影矩阵方法［J］.宇航学报，2006，27(4):609 －615.［Zhang Jun，Xu Shi-jie.A projection matrix approach for design of IPACSof spacecraft with VSCMGs［J］.Journal of Astronautics，2006，27(4):609 －615.］

［5］ 刘向东，辛星，从炳龙，等.以VSCMG为执行器的航天器姿态机动自适应动态滑模控制［J］.宇航学报，2012，33(8):1064 －1071.［Liu Xiang-dong，Xin Xing，Cong Bing-long，et al.An adaptive dynamic sliding mode attitude maneuver control law for rigid body satellites using VSCMG actuator［J］.Journal of Astronautics，2012，33(8):1064 －1071.］

［6］ 宋斌，李传江，马广富.航天器姿态机动的鲁棒自适应控制器设计［J］.宇航学报，2008，29(1):121 －125.［Song Bin，Li Chuan-jiang，Ma Guang-fu.Robust adaptive controller design for spacecraft during attitude maneuver［J］.Journal of Astronautics，2008，29(1):121 －125.］

［7］ Jin Y Q，Liu X D，Qiu W，et al.Time-varying sliding mode controls in rigid spacecraft attitude tracking［J］.Chinese Journal of Aeronautics，2008，21(4):352 －360.

［8］ Jung D，Tsiotras P.A 3-DoF experimental test-bed for integrated attitude dynamics and control research［C］.AIAA Guidance，Navigation，and Control Conference，Austin，Texas，2003.

［9］ Dai L，Jin G.A 3-axis simulator for spacecraft attitude control research［C］. 2010 IEEE International Conference on Information and Automation， Harbin， Heilongjiang， China，2010.

［10］ Panagiotis T.Stabilization and optimality results for the attitude control problem［J］. Journal of Guidance， Control， and Dynamics，1996，19(4):2 －3.

［11］ David A D.Adaptive attitude control and closed-loop power tracking for an integrated power and attitude control system using variable speed control moment gyroscopes［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，San Francisco，California，August 15－18，2005.

［12］ 楚中毅，任善永.带柔性伸杆小卫星振动控制的半物理仿真实验［J］.宇航学报，2013，34(6):748 －754.［Chu Zhong-yi，Ren Shan-yong.Semi-physical simulation on vibration control of small satellite with flexible manipulators［J］. Journal of Astronautics，2013，34(6):748 －754.］