广播星历参数物理意义分析与相关性研究

黄 华，何 峰，刘 林

(1.61876部队，三亚572022;2.北京卫星导航中心，北京100094;3.南京大学天文与空间科学学院，南京210093)

0 引言

广播星历参数的拟合精度与稳定性直接影响卫星导航系统的服务性能，目前广播星参数模型主要有两种，一种是GPS采用的基于开普勒根数及其摄动变化量的星历模型，另一种是GLONASS采用的基于卫星位置速度和简化动力学模型参数的星历模型。GPS采用的16参数模型具有拟合精度高，用户算法简单等特点，此后发展的卫星导航系统基本都采用类似参数模型。导航卫星轨道几何特征和动力学特征是广播星历参数设计的重要依据。GPS星座由周期大约12小时、轨道倾角约55度的MEO卫星组成，其广播星历参数的设计主要针对该类卫星。GEO卫星的轨道几何和动力学特征与MEO存在较大差异，如果采用传统方法进行拟合，各参数之间相关性较强，而且存在部分参数变化幅度偏大等问题。国内的很多专家和学者对GPS广播星历参数模型在GEO卫星中的运用进行了研究和探讨。文献［2］研究了GEO卫星广播星历拟合中出现的Δn变化幅度过大和出现半月振荡周期等问题，提出了基于参数岭估计的解决方案，文献［3］、［6］对比分析了18参数和16参数两种广播星历模型之间的差别。本文主要通过研究GPS广播星历参数的物理意义，进一步分析不同类型卫星拟合中参数间的相关性，最后探讨GPS广播星历参数对GEO卫星拟合不稳定的内在原因，为混合星座(由GEO，IGSO，MEO卫星组成)的广播星历参数设计以及拟合算法研究提供参考，进一步提高卫星导航服务精度和稳定性。

1 导航卫星轨道变化规律

导航卫星轨道高度较高，主要摄动源包括地球非球形引力、日月引力和太阳辐射压。从卫星轨道运动分析解［1］中可以看出，在以上主要摄动力作用下，导航卫星轨道变化存在以下几个特征:

(1)地球非球形引力和日月引力属于保守力，太阳辐射压在理想模型(球模型)和不考虑地影的情况下也属于保守力，因此轨道没有能量耗散，轨道半长径A无长期变化项;

(2)由于地球非球形引力田谐项共振的影响，MEO、GEO和IGSO卫星轨道半长径都存在一阶(J2的量级)长周期项，其中GEO和IGSO卫星的一阶长周期项量级比MEO大;

(3)偏心率e不存在长期变化，在非球形引力J3项和太阳辐射压的影响下存在一阶长周期项;

(4)轨道倾角i没有长期变化项，但在日月引力摄动下存在一阶长周期项;

(5)升交点赤经Ω、近点角距ω和平近点角M存在一阶长期变化项和一阶长周期变化项;

(6)所有轨道根数都存在短周期变化项。短周期项的频谱分布为:最大项为半轨道周期项，其次是1倍轨道周期和3倍轨道周期项，大小与半轨道周期项相差一个偏心率因子。

由以上特征可以将轨道根数的变化用以下公式表达:

其中短周期项可写成如下形式

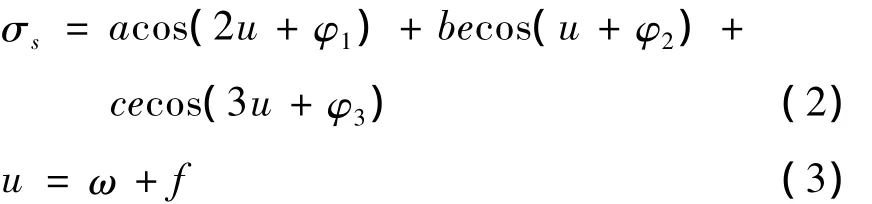
2 广播星历参数物理意义分析

导航系统卫星精密轨道不采用普通的多项式或其它纯数学意义的参数拟合，而是设计具有一定物理意义的广播星历参数，可以获得更高的拟合精度和更强的预报能力。下面针对广播星历参数物理意义做一些分析。

GPS广播星历参数拟合弧长一般采用2到3个小时，短弧条件下长周期项的影响与长期项相近。

由第1节中对轨道摄动变化特征的介绍，GPS的16 参数广播星历模型中，(，e，i0，Ω0，ω0，M0)表达参考时刻的平根数(Ω0的意义与惯性系下的值并不一致)。

(Crs，Crc，Cus，Cuc，Cis，Cic)为短周期项改正的振幅，对应的改正项幅角为2u，广播星历中短周期项的改正项表达式为［4］:

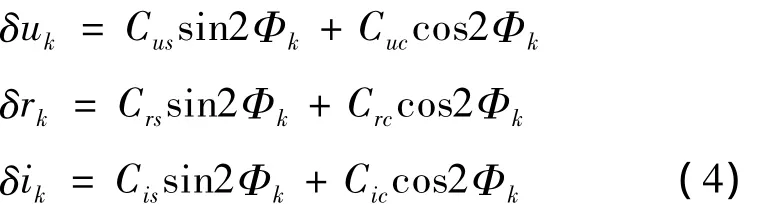
解算正弦和余弦项振幅与解算余弦项振幅和相位等价，从式(4)可以看出，这6个参数只改正了短周期项的主项，即式(2)中的a cos(2u+φ1)项。广播星历参数并没有针对每一个轨道根数做短周期项修正，而是对沿迹向幅角u、径向距离r以及轨道倾角i进行修正。如果对每一个轨道根数都做短周期项修正，总的短周期项修正参数将达到12个，参数太多对星历的拟合也会带来不利的影响。所有的短周期项都可以归算到三轴分量上，即R、T、N方向，对径向距离r的修正实际上相当于对径向R方向的修正，对沿迹向幅角u的修正相当于对切向T方向的修正，对轨道倾角i的修正相当于对轨道面法向N方向的修正，只需6个参数就可以表达对轨道的短周期项修正。广播星历的短周期改正项只吸收了短周期项的主项，其余的周期项残留在了其他参数当中，对不同参考时刻的星历参数作图［6］就可以看出这一点，主要是与u，3u相关周期项。

Δn为平均角速度的修正值，导航卫星的偏心率较小，对于MEO和IGSO卫星来说，主要吸收了M和ω的长期项和长周期项，Ω·吸收了Ω的长期项和长周期项，idot吸收了i的长周期项。GPS新的18参数广播星历模型新增的两个参数为半长径A的变化率A·和Δn变化率Δ˙n，A·主要吸收半长径的长周期项，Δ˙n主要吸收由A·引起的卫星运动角速度变化率。

与短周期项修正参数的考虑一样，长期项和长周期项的修正实际上也相当于加在三轴方向，Δn为沿迹向修正，idot和Ω·为轨道面整体摆动的修正。在拟合弧段较短的情况下可以不考虑径向的长周期变率，因此16参数模型中并没有针对径向的长期修正项，18参数模型引入了径向相关的长期项修正参数即半长径A的长期变化率，有利于进一步提高拟合精度。

3 广播星历参数相关性

利用经典拟合方法［5］对倾角为55度的MEO卫星轨道数据进行拟合，拟合弧段为3小时，轨道数据历元间隔5分钟。表1～表3给出了部分参数之间的相关系数(由于篇幅限制，这里不再列出所有参数之间的相关系数)，具有以下特点:

(2)参数 i0，Ω0，Cis，Cic，idot，Ω·之间相关性较强;

(3)Δn与所有参数的相关性基本相同。广播星历参数计算卫星位置的算法中最后一个公式［4］为:

表1 MEO卫星■A与其他参数的相关系数表Table 1 The correlation of■A and other parameters for MEO satellites

表2 MEO卫星i0与其他参数的相关系数表Table 2 The correlation of i0 and other parameters for MEO satellites

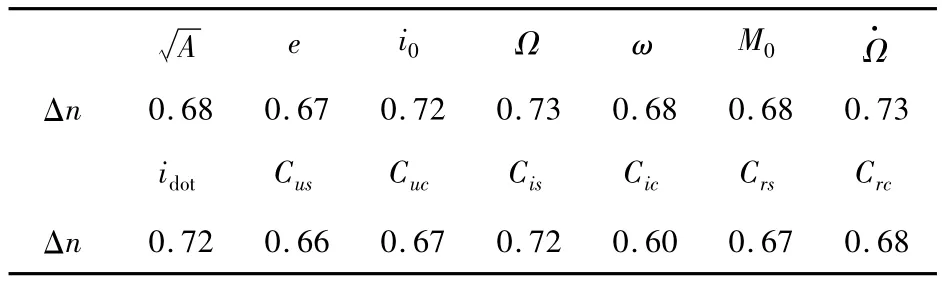
表3 MEO卫星Δn与其他参数的相关系数表Table 3 The correlation ofΔn and other parameters for MEO satellites

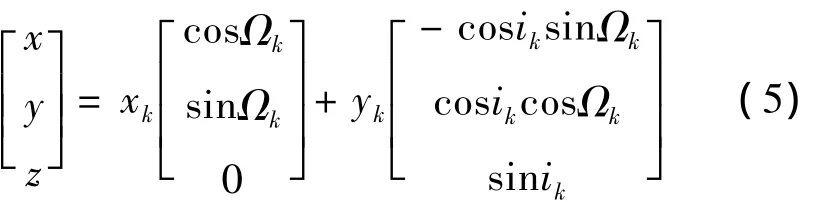
其中 xk、yk由，e，ω0，M0，Crs，Crc，Cus，Cuc以及 Δn得出，ik、Ωk由 i0，Ω0，Cis，Cic，idot，Ω·确定。xk、yk决定了位置矢量的大小和在轨道面内的指向，而ik、Ωk则决定了轨道面的空间指向，因此它们各自之间的相关性较强。Δn平均角速度的修正值，其中与日月引力相关的项为后面的式(8)，当轨道倾角较大(55度)时，Δn由A，e，i，Ω决定，所以它与其他参数的相关性基本相同;当i接近0时，Δn的大小主要由i决定，因此它与表达轨道面定向参数之间的相关性会增大，表4给出了GEO卫星Δn与其它参数之间的相关系数，Δn 与 i0，Ω0，Cis，Cic，idot，Ω·的相关性明显增大。

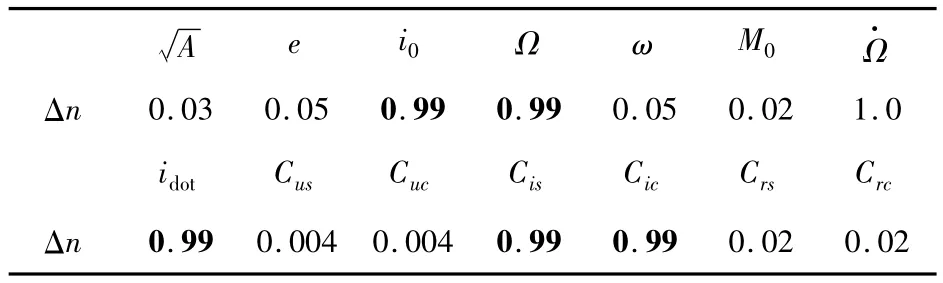
表4 GEO卫星Δn与其他参数的相关系数表Table 4 The correlation ofΔn and other parameters for GEO satellites

4 GEO卫星的小倾角问题

GEO卫星与IGSO/MEO卫星轨道几何特征的差别之一在于其轨道倾角较小，基于开普勒根数的广播星历参数本身具有一定奇异性，即存在小倾角奇点。

4. 1 Δn等参数振幅的分析

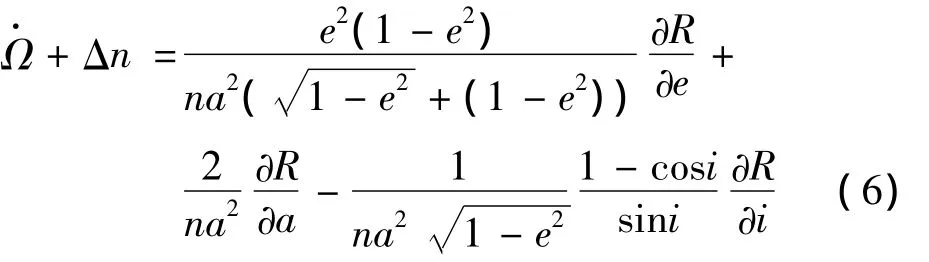
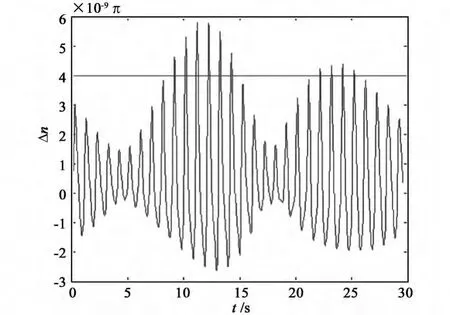
对GEO卫星轨道拟合还发现，Δn的变化有半月周期［2］，如图2 所示。

地球的非球型引力J2项和日月引力是GEO卫星的主要摄动力。J2项摄动引起的Δn一阶长期项如下式:

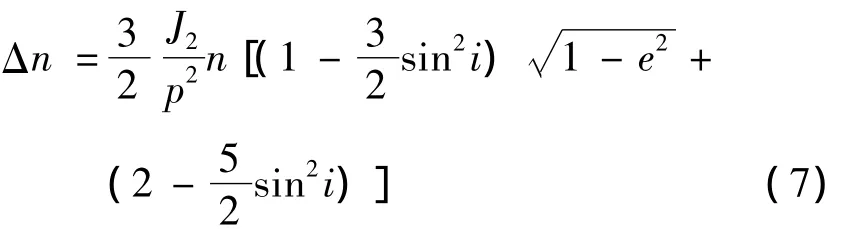
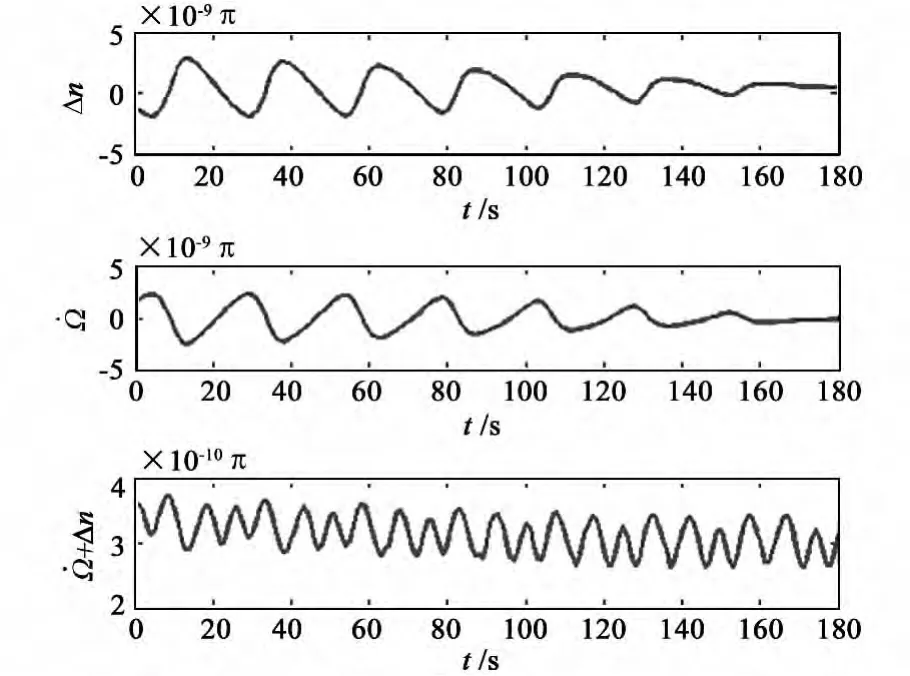
图1 Δn、+ Δn 变化图Fig.1 The evolution ofΔn， + Δn

其中 p=a(1 －e2)，J2=1.082 63 ×10－3，当i=5°，a=42 165 725.844m，e=1.0 × 10－4时，J2引起的Δn=2.5×10－9(用 π 量化，即将标准单位(弧度 /秒)对应的值再除以π)，由式(7)可以看出，J2引起的长期项中不包含奇点，不会引起Δn超限，日月引力摄动的长期项也不含奇点，且量级比J2小，所以也不可能造成超限问题。J2引起的长周期项没有奇点，也不可能造成超限现象。日月引力引起Δn的长周期项中含有奇点，包含奇点的项为:

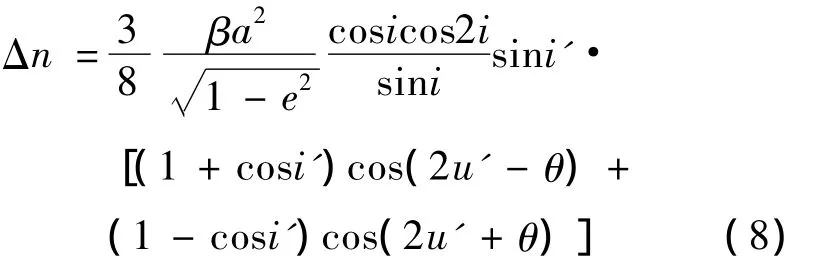
其中β=m'/(r')3，m'为摄动天体的质量，r'为摄动天体到地球的距离，i'为摄动天体轨道倾角，u'=2中Δn变化幅度增大且出现半月周期的原因。量级估算为:

i=1°，a=42 165 725.844m，e=1.0 × 10－4时，Δn=7 × 10－9;

i=5°，a=42 165 725.844m，e=1.0 × 10－4时，Δn=1.5 × 10－9。

由此可见i=1°比i=5°引起的Δn要大许多。但在i=5°的情况下，Δn的变化范围仍然较大。

4. 2 对拟合稳定性的影响

造成GEO卫星拟合效果不佳和部分参数振荡范围增大的主要原因是参数之间的相关性太强，特别是在小偏心率和小倾角两个奇点的同时影响下，Δn和Ω·的相关性太强，甚至可能接近线性相关的条件，这种情况下会导致拟合的法方程病态，最终导致拟合发散。在e→0，i→0的情况下:ω'+M'为摄动天体近地点角距与平近点角之和，θ=Ω－Ω'为升交点赤经与摄动天体升交点赤经之差。式(8)表明，Δn的长周期变化项周期为摄动天

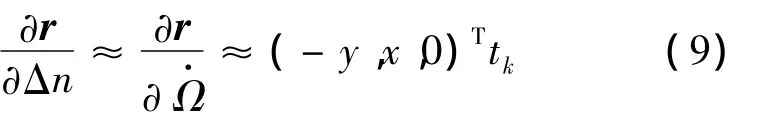
tk=t－toe，为数据历元与参考历元之差。这种情况下法方程将出现亏秩现象，导致拟合难以收敛。

4. 3 解决策略探讨

小倾角引起的奇点并不是本质奇点，而是由于坐标系的选取不当导致，有学者提出了坐标系基本参考面旋转一个角度的方法来改善GEO卫星的拟合效果［5］，相当于重新选取坐标系。只改变坐标系基本参考面的情况下，新的坐标仍然是惯性系，卫星在新坐标系下的摄动变化规律基本不变，轨道形状的变化规律无论在那个惯性系下都不会变，轨道面整体的南北摆动、西退或东进等规律也不会变，因此，在新坐标下各参数的值有所变化，但其物理意义并没有严重扭曲，新坐标系下不存在小倾角引起的奇点，参数的振幅变小，法方程的病态性也得到了很大改善，不会出现拟合发散的现象。图3给出了倾角为1度的GEO卫星，坐标系旋转55度以后Δn与Ω·的变化图，可以看出，Δn和Ω·的变化幅度都比图1小。

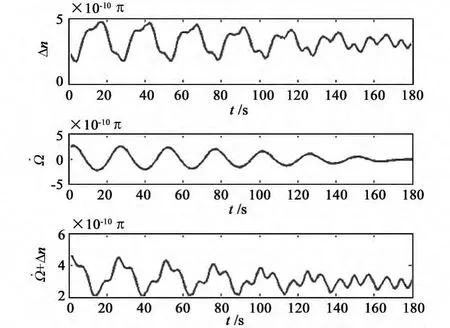
图3 GEO 卫星 Δn、Ω· 以及Ω· + Δn变化图Fig.3 The evolution ofΔn，Ω· and Ω· + Δn for GEO satellites

5 结论

通过对广播星历参数物理意义和参数之间相关性的分析得出以下几点结论:

(1)广播星历参数的设计基本依据了卫星轨道的几何和动力学特征，对于MEO卫星，参数之间相关性的特点是:反映卫星位置矢量大小及其在轨道面内指向的参数之间相关性较强，表征轨道面定向的参数之间相关性较强，Δn与所有参数的相关性一样。

(2)GEO卫星广播星历拟合过程中Δn与表征轨道面定向的参数之间相关性增大，主要原因是小倾角条件下参数奇异性的影响，这也是导致拟合过程中Δn变化幅度偏大和部分情况下拟合发散的根本原因。

(3)GEO卫星拟合中的小倾角奇点问题主要反应在日月引力摄动中，这是GEO卫星广播星历参数Δn出现半月振荡周期的原因。

(4)通过将坐标系基本平面旋转一定角度可以改善GEO卫星的拟合效果，角度的选择不宜太小，否则仍然可能出现参数超限现象。

［1］ 刘林.航天器轨道理论［M］.北京:国防工业出版社，2000.

［2］ 何峰，王刚，刘利，等.地球静止轨道卫星广播星历参数拟合与实验分析［J］.测绘学报，2011，40(5):52 －58.［He Feng，Wang Gang，Liu Li，et al.Ephemeris fitting and experiments analysis of GEO satellite［J］.Acta Geodaetica et，Cartographica Sinica，2011，40(5):52 －58.］

［3］ 崔先强，焦文海，贾小林，等.两种GPS广播星历参数算法的比较［J］.空间科学学报，2006，26(5):382－387.［Cui Xianqiang，Jiao Wen-hai，Jia Xiao-lin，et al.Comparisons of two kinds of GPSbroadcast ephemeris parameter algorithms［J］.Chin.J.Space Sci，2006，26(5):382 －387.］

［4］ Hegarty CJ.GPS原理与应用［M］.寇艳红译.北京:电子工业出版社，2007.

［5］ 刘光明，廖瑛，文援兰，等.广播星历参数拟合算法研究［J］.国防科技大学学报，2008，30(3):100－104.［Liu Guangming，Liao Ying，Wen Yuan-lan，et al，Research on the fitting algorithm of broadcast ephemeris parameters［J］.Journal of National University of Defense Technology，2008，30(3):100－104.］

［6］ 黄华，刘林，周建华，等.18参数广播星历分析研究［J］.飞行器测控学报，2012，31(3):80－84.［Huang Hua，Liu Lin，Zhou Jian-hua， et al. Research on 18 elements broadcast ephemeris model［J］.Journal of Spacecraft TT＆C Technology，2012，31(3):80 －84.］

［7］ Van Dierendonck A J，Russel SS，Kopitzke E R，et al.The GPS navigation message［J］.Navigation，1978，25(2):147 －165.

［8］ 文援兰，刘光明，张志.基于无奇异变换的卫星广播星历拟合算法［J］.宇航学报，2011，32(12):2478－2483.［Wen Yuan-lan，Liu Guang-ming，Zhang Zhi.Research on the fitting algorithem of broadcast ephemeris parameters based on no-singular transformation［J］.Journal of Astronautics，2011，32(12):2478－ 2483.］