小推力最优轨道转移问题的UKF估计算法

李 鉴，韩 潮

(北京航空航天大学，北京100191)

0 引言

小推力推进系统具有比冲高、消耗工质少，有效载荷比高，体积小，工作时间长，推力精确可控等特点，所以在空间任务中得到越来越多的应用。

小推力轨道转移具有机动时间长，非线性强的特点，其优化问题一直是空间轨迹优化领域的研究热点和难点，目前主要的研究内容是时间最短轨道转移问题和燃料最优轨道转移问题。就数值解法而言，连续推力轨迹优化的求解方法可分为直接法和间接法。直接法通过不同的离散化方法对控制量进行参数化，把轨道优化问题转化为带有约束的参数优化问题，然后采用非线性规划算法进行求解。这类方法目前的研究热点是伪谱法［1－2］，该方法与传统方法相比具有求解精度较高，寻优参数少，收敛性好的优点，但它仍然需要猜测初值，而且严重依赖非线性规划软件的求解能力。目前所见文献中，用伪谱法求解小推力最优轨道转移问题多局限于同平面圆轨道之间。对于大尺度长时间小推力轨道机动问题，其求解效果尚不明确。

间接法主要通过变分法和极大值原理将原始的连续推力轨迹优化问题转化为两点边值问题，然后利用各种数值方法来求解该问题，常用的方法为打靶法。在应用打靶法求解两点边值问题时，有3个难点:(1)需要获取目标函数或者终值误差函数对于状态量和协态变量的梯度矩阵，这些矩阵推导复杂，并且可能出现病态。一般采用数值微分方法避免推导，但精度有限。(2)打靶法对于两点边值问题中的协态变量初值很敏感，收敛半径小，而协态变量又缺乏物理意义，难以估计初值。于是一部分学者研究了协态变量的初值猜测技术，如鲁棒性算法［3］，进化算法［4］和粒子群算法［5］。随机搜索算法虽然可以得到全局最优解，但是计算效率太低，不适合需要长时间积分的小推力轨迹优化问题。Lee［6］提出了一种新的螺旋形轨道协态变量初值猜测方法，但仅适用于平面内轨道机动。(3)控制切换时刻不易确定，文献［7］提出了控制切换点的搜索算法，但无法保证一定能获得全部控制切换点。

文献［8－10］通过构造两层同伦，以控制连续、求解相对容易的能量最优问题解作为初值，逐步逼近燃料最优问题的解。这样使每一层优化问题都获得了良好的协态变量初值，克服了协态变量初值猜测的困难。文献［11］在文献［9］算法基础上对协态变量进行归一化处理，并加入控制切换点搜索算法和粒子群算法以获取全局最优解。同伦法具有较高的稳定性、精确性和求解效率，是目前小推力轨迹优化文献中最有效的算法。但是它引入了两个新的优化问题，需要另外构造其最优控制律和相关的梯度矩阵，增加了求解的繁琐程度，并且还需要使用同伦算法程序包，这些都增加了该算法对于工具软件的依赖程度。

针对上述研究现状，本文提出一种基于UKF参数估计算法的小推力最优轨道转移问题求解方法，将轨道机动最优控制问题所对应的两点边值问题转化为参数估计问题，然后用UKF滤波器进行参数估计。该方法流程简单，不依靠强大的非线性规划软件包。其基本原理是估计理论，不依赖梯度信息，故不需要良好的协态变量初值，也不用推导梯度矩阵，同时又具有较好收敛性和精确性，可以很好地解决小推力轨道机动优化问题。

1 小推力轨道最优轨道转移问题

1. 1 原始优化问题描述

小推力轨道转移的时间历程通常很长，飞行圈数可达几百甚至上千圈，如果采用直角坐标描述航天器的运动会导致状态量的时间历程振荡剧烈，不利于快速积分。本文采用改进春分点轨道要素来描述航天器的轨道运动，这样既有利于提高积分速度和精度，又避免了可能出现的奇点问题。改进春分点轨道要素［p，ex，ey，hx，hy，L］与经典 Kepler 轨道要素的关系如公式(1)所示:

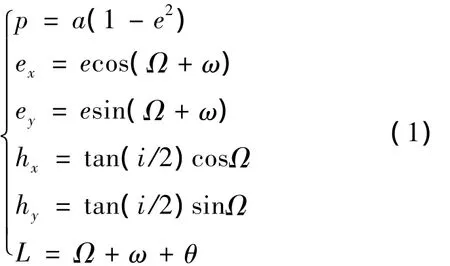
式中:p为轨道半通径，a为轨道半长轴，e为偏心率，i为轨道倾角，Ω为升交点赤经，ω为近地点幅角，θ为真近点角。同时，定义如下辅助变量:

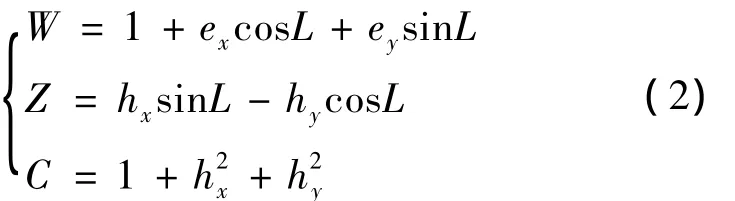
以改进春分点轨道要素表示的航天器轨道动力学方程为:

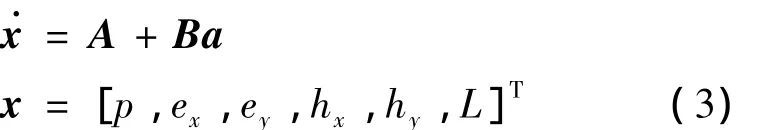
式中:

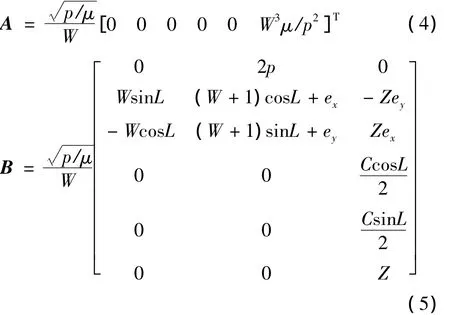
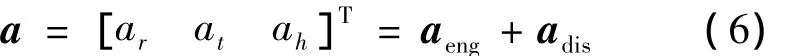
式(6)中，a为除二体引力加速度之外的其他外力加速度矢量，［ar，at，ah］T为 a 在轨道径向、垂直于径向和动量矩方向的分量，aeng为发动机推力加速度矢量，adis为其他摄动加速度矢量。本文的讨论范围为只有二体引力加速度和发动机推力加速度情况下的小推力轨道机动优化问题，其他摄动加速度的影响将在后续工作中研究。为简化起见，在后文公式中用a代替aeng作为发动机推力加速度矢量。

设航天器质量为m，发动机推力大小具有上限Tmax和常值比冲Isp，g0=9.780 4m/s2为赤道重力加速度，则方程(3)～(6)可改写为

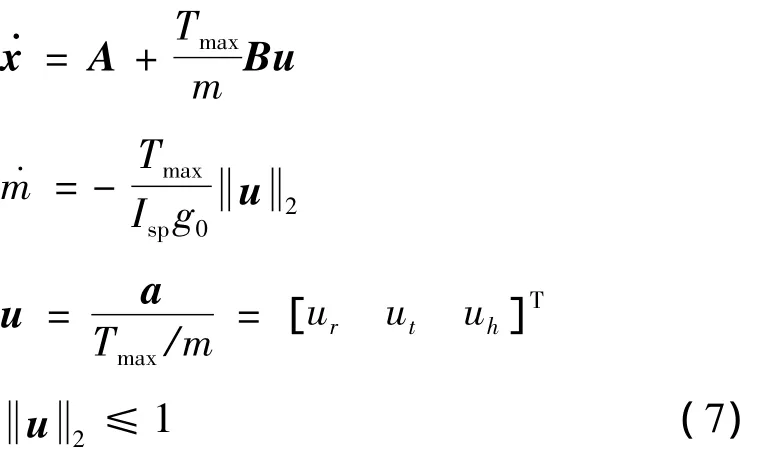
1. 2 最优控制两点边值问题

要求解MF问题必须先求解TF问题，因为MF问题的飞行时间必须大于求解TF问题所得的最短飞行时间tfmin。本文基于极大值原理求解最优控制问题，由文献［9－10］可知，TF问题与MF问题所满足的状态变量与协态变量微分方程形式一致，两种问题的最优控制律也具有相似的形式。应用本文提出的算法求解TF问题与MF问题的过程完全相同，并且TF问题更容易求解，因此将MF问题作为讨论重点，对TF问题只给出求解结果以便与文献的算例作比较。

引入与改进春分点轨道要素对应的协态变量λ= ［λp，λex，λey，λhx，λhy，λL］T和与质量对应的协态变量λm。MF问题的Hamilton函数为:

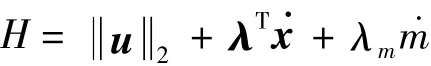
其中α为矢量u与BTu之间的夹角。与终端状态~x(tf)和终端时刻tf相关的性能指标K为:

状态约束为:

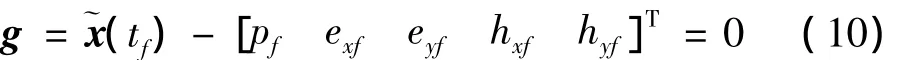
系统定常，根据极大值原理，最优控制的必要条件为:

状态与协态方程:

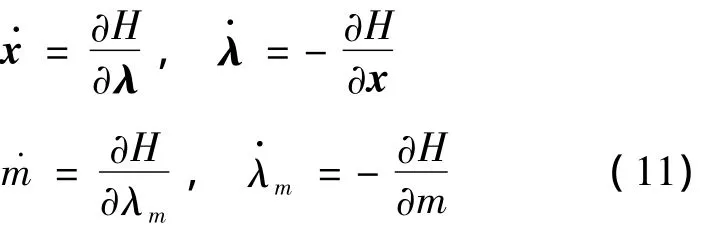
初始条件:

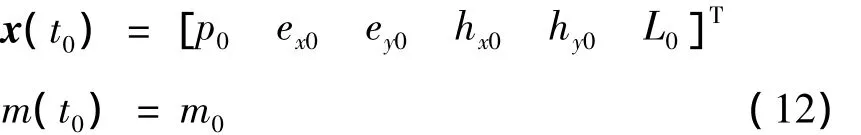
引入状态约束g的拉格朗日乘子ν，则末值条件为:

Hamilton函数对最优控制u*有极小值，即:

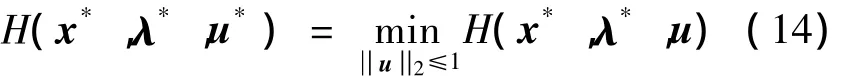
由式(8)和(14)可知，控制取最优时α=π。系统定常，Hamilton函数不显含时间，故当控制取最优时H在［t0，tf］上为常数。

考察λm的方程

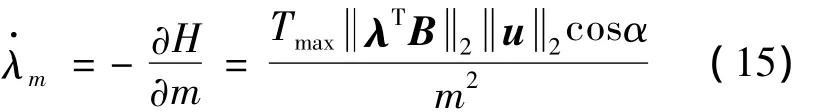
易知当α=π时，λm的导数非正。又由式(13)可得当控制为最优控制时，tf时刻λm应为0，故λm在［t0，tf］上非负，这一结论对TF问题也成立。令开关函数ψ为:

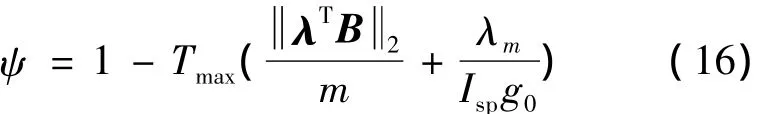
由文献［9］可知最优控制律应具有如下形式:

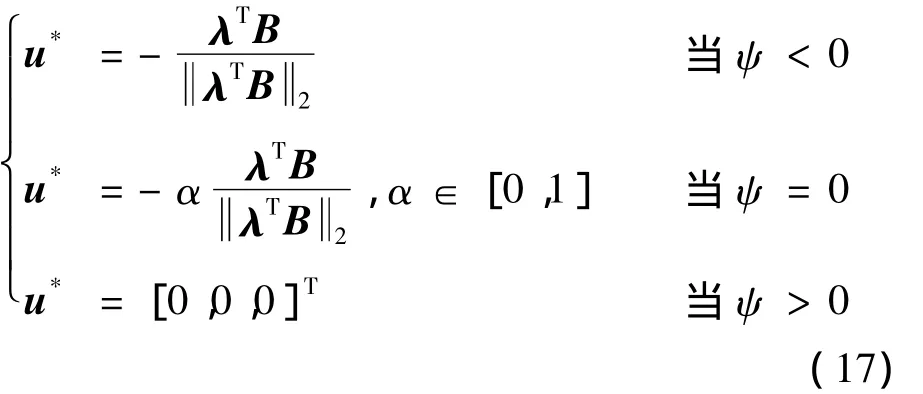
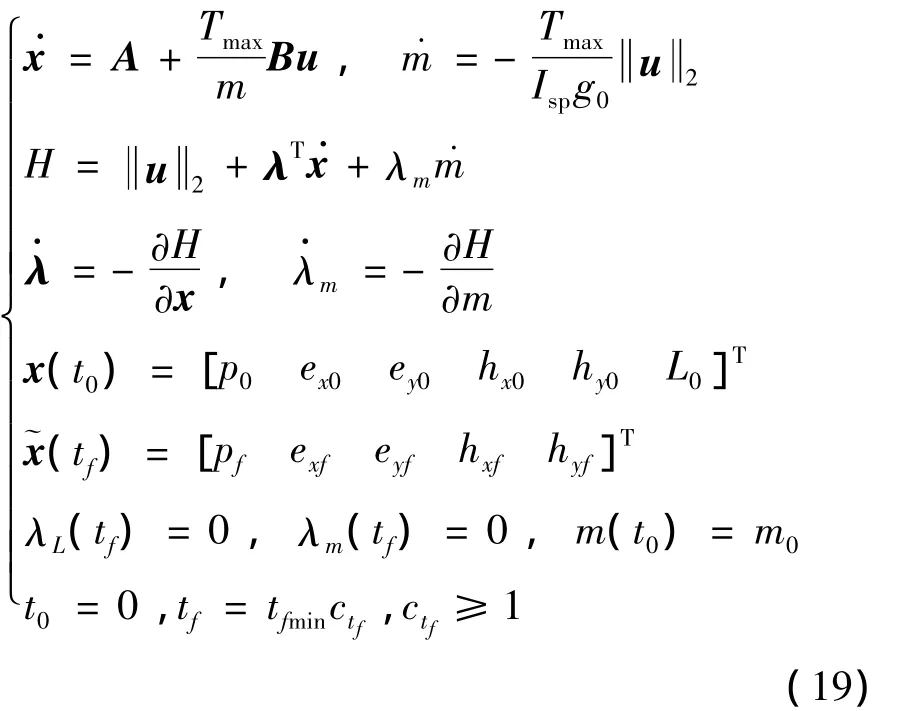
下面讨论如何将上述两点边值问题改写成参数估计问题，然后利用UKF滤波估计算法求解。

2 UKF参数估计及其求解方法

参数估计问题，又被称为系统辨识或者机器学习问题，其目的是为了确定一个非线性映射:

该映射的输入为xk，输出为yk，w为非线性映射的参数。一般来说，映射输入xk和期望输出dk是不变的，输出误差定义为ek=dk－G(xk，w)，求解参数估计问题就是要估计w的均值，使映射G(xk，w)的输出误差最小。用滤波器求解参数估计问题的相关理论，文献［12］作了详细阐述，本文只作简要介绍。

将原始参数估计问题写成状态空间表达式:

上式代表一个状态转移矩阵为单位阵的静态过程，rk为过程噪声，而期望输出dk则与对wk的非线性观测相对应，ek为观测噪声。这样，原参数估计问题就可以用EKF，UKF等滤波器求解。基于UKF滤波器的参数估计算法流程［12］如图1所示。

图1 UKF参数估计算法Fig.1 UKF parameter estimation

UKF参数估计算法公式中，

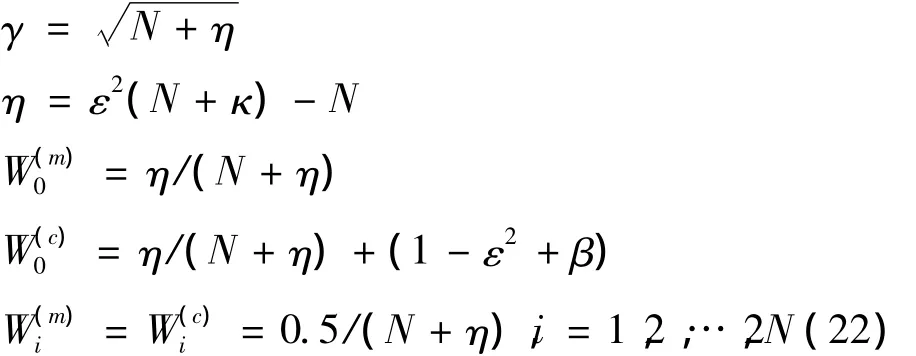
Rr和Re分别是过程噪声和观测噪声的协方差阵。N是w的维数，η是尺度参数，常量ε决定了UT变换的σ点相对于w当前均值的分布范围，一般设为小量，取值范围为［10－4，1］。常量 κ 也是个尺度参数，一般取为0或者3－N。β是与w的先验分布相关的常量，对于高斯分布，β=2是最优的。ρRLS是遗忘因子，用于防止因模型误差较大造成的滤波发散，其取值范围为(0，1］。关于这些常量选取方法的详细讨论可以参看文献［12］。

参数估计问题相当于求解如下以w为优化变量的优化问题:

式(23)中

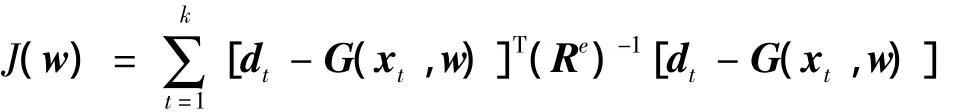
定义观测误差为qk=dk－G(xk，wk)，将式(21)重写为如下观测误差形式:

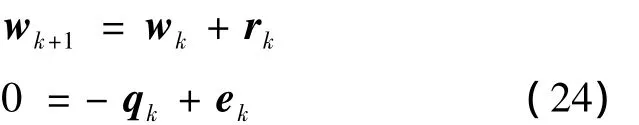
上式表明观测误差的期望值为0，求解原始参数估计问题最终转化为求解式(24)所代表的非线性过程的参数估计问题。

3 UKF参数估计算法求解小推力最优轨道转移问题

将式(19)代表的燃料最优两点边值问题改写为参数估计问题，选择待估计参数w为:

观测误差为q:

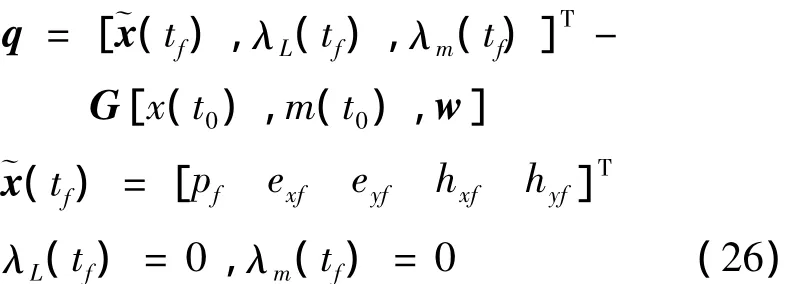
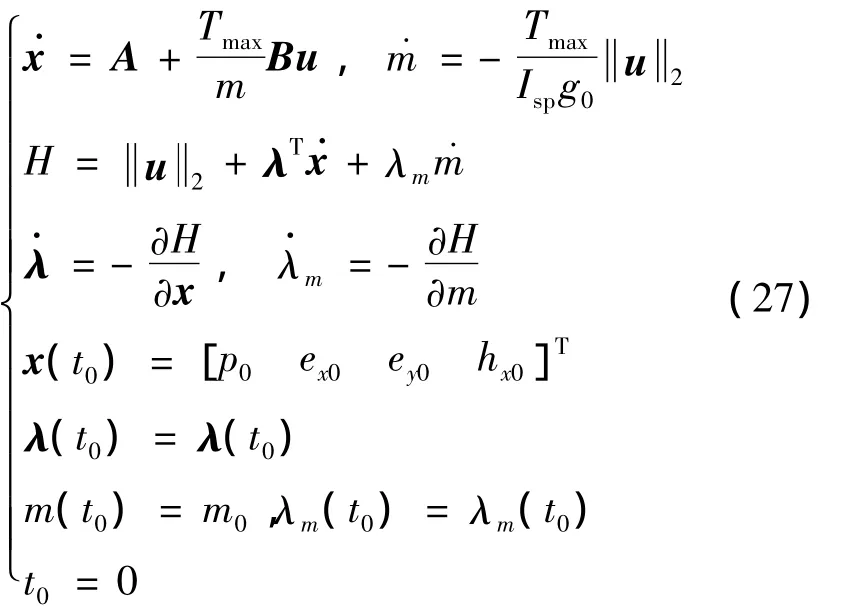
其中G为如下微分方程组初值问题的解:至此，TPBVPMF问题(19)与式(24)形式上一一对应，已转化为参数估计问题，可通过UKF参数估计算法求解。

4 数值算例与结果分析

首先求解TF问题。以表1给出的初末轨道参数和发动机参数为例，求解不同最大推力值下的时间最短小推力轨道转移问题，并将计算结果(由PE法表示)与同伦法的计算结果［10］作比较，如表2所示。

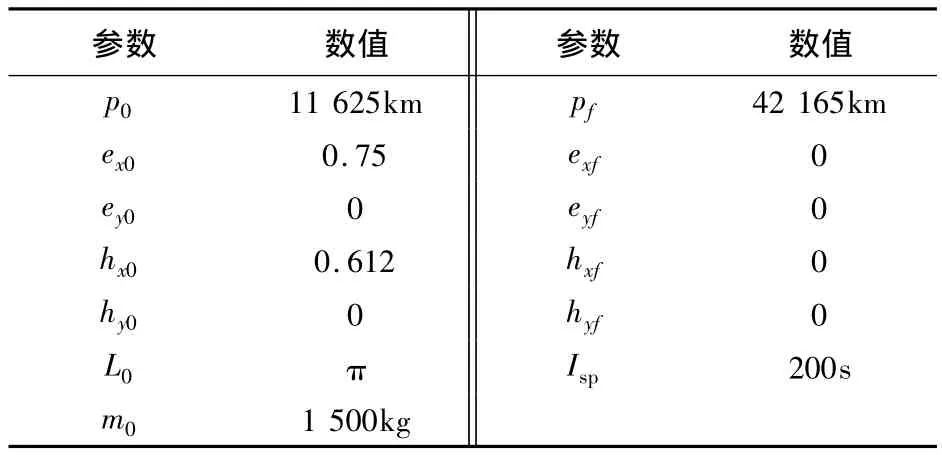
表1 初始计算参数Table 1 Initial parameters

PE法可以直接用随机初值得到Tmax=0.01N时TF问题的解，文献［10］只给出了直至Tmax=0.14N时的计算结果，所以在表中没有数据。

文献［8］证明了当最大推力值趋近于0时，最小转移时间和最大推力值之间存在如下简单关系:

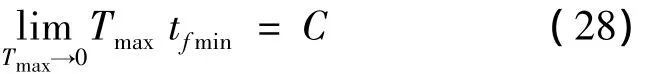
式中C为常数，仅与机动过程的初末轨道参数和发动机参数相关。表2中的PE数据是完全符合上述关系式的，也说明本文算法能够正确求解时间最短小推力轨道转移问题。

表2 最短轨道转移时间Table 2 Minimum transfer times

下面以表1给出的初末轨道参数、发动机参数为例，取飞行时间参数ctf=1.5，求解不同最大推力值下的燃料最优小推力轨道转移问题，并在表3中与同伦法的计算结果作比较。

文献［9］所给出的计算条件为SUN-Blade 1 000，本文所得数据的计算条件为Intel i3 3.10GHz，由于没有确切的计算能力参数，只能根据CPU的浮点计算能力估计后者的计算能力是前者的10倍。由表3可见，两种方法的求解效率大致相当。

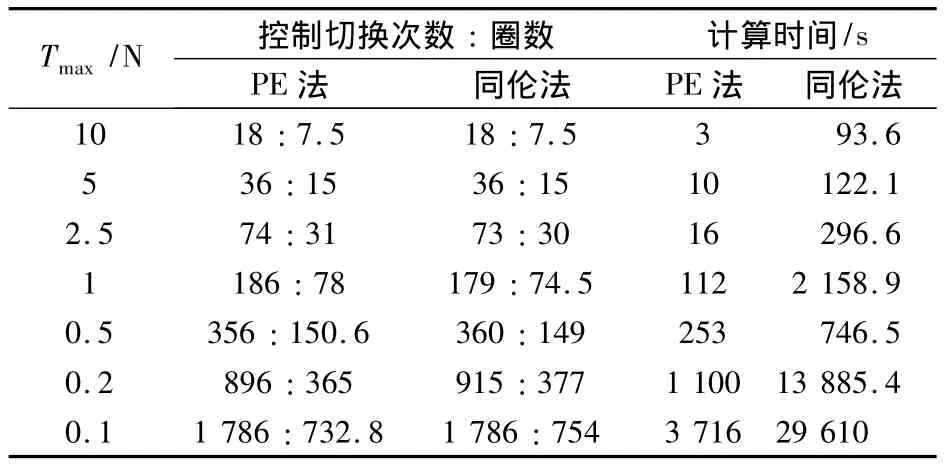
表3 不同T max情况下的燃料最优轨道转移问题控制切换次数和计算时间Table 3 Switches and computation times of fuel-minimum orbit transfer problem with various T max

可以看出在推力较大的情况下两者的计算结果是非常吻合的。当推力小于1N时，结果出现了差别，但由表中数据算出的比值仍然是吻合得比较好的，基本上保证了一圈内有2次控制切换，这与文献［9］中得出的结论一致。数据的差别可以解释为两种方法得到了不同的局部最优解。文献［9］明确指出，求解小推力TPBVPMF问题(19)时极易陷入局部最优解，其具体表现就是相同的飞行时间对应不同的Lf，即不同的飞行圈数。事实上，文献［9］得到的最优解最终剩余质量大约为1 382kg，而本文算法得到的最终剩余质量约为1 378kg，从实际应用角度出发，这个偏差是可以接受的。

为了验证本文方法所得结果的精确性，下面以Tmax=10N为例求解TPBVPMF问题(19)，结果如图2～图3所示。对比图2～图3和文献［9］的图示结果，两者几乎是完全一致的。图3中Hamilton函数值在整个机动过程中近似保持不变则验证了所得结果的最优性。

5 问题与经验总结

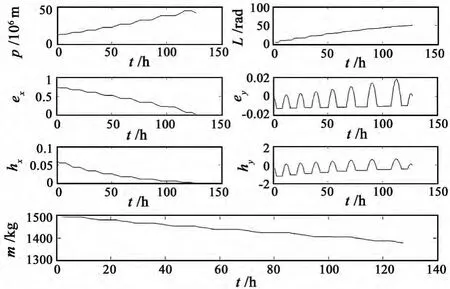
图2 燃料最优轨道机动问题最优解的轨道要素随时间变化历程(最大推力值为10N)Fig.2 Modified equinoctial elements vs time for minimum-fuel orbit transfer problem(T max=10N)

图3 燃料最优轨道机动问题的最优控制量和Hamilton函数随时间变化历程(最大推力值为10N)Fig.3 Optimal control and Hamilton function vs time for minimum-fuel orbit transfer problem(T max=10N)

(1)应用UKF参数估计方法，协态变量初值可以随机选取，但λm的初值一定要为正。初值的选取范围与构造问题时使用的量纲是紧密相关的。本文所有算例的长度量纲为106m，时间量纲为小时，以便与文献［9］对比结果，不一定是最优的选择。针对不同的轨道转移问题，选取合适的量纲，使各个协态变量量级尽量接近，可以提高求解效率。

(2)UKF滤波算法公式中的过程噪声Rr、常量ε和遗忘因子ρRLS对滤波收敛过程的影响很大。这些量的选取和更新方法属于UKF滤波器算法改进范畴，不是本文的讨论重点，可以作为下一步工作。本文通过大量数值仿真，总结常量ε和遗忘因子ρRLS的选取和更新方法如下:对于常量ε，滤波初始阶段ε应尽量取较大值(如0.8)，随着滤波迭代的进行，ε应该随观测误差的减小而减小，这样有利于算法的快速收敛。本文的算例中，ε最终可减小至0.001。对于遗忘因子ρRLS，当遗忘因子ρRLS较小时，滤波过程的振荡幅度很大，反之则振荡幅度较小。推力较大时(1N/1 500kg左右)，采用较小的 ρRLS(如 0.2 ～0.3)，滤波可以很快收敛。当推力较小时，则应采用较大的 ρRLS(如0.5 ～ 0.7)。

6 结论

本文提出的基于UKF参数估计算法的小推力轨道转移优化设计方法具有简洁、精确、高效的优点，可作为求解小推力轨道机动优化问题的一个有力工具。

［1］ Ross I M，Gong Q，Sekhavat P.Low-thrust，high-accuracy trajectory optimization［J］.Journal of Guidance and Control，2007，30(4):921－933.

［2］ 尚海滨，崔平远，徐瑞，等.基于高斯伪光谱的星际小推力转移轨道快速优化［J］.宇航学报，2010，31(4):1005－1011.［Shang Hai-bin，Cui Ping-yuan，Xu Rui，et al.Fast Optimization of interplanetary low-thrust transfer trajectory based on Gauss pseudospectral algorithm［J］.Journal of Astronautics，2010，31(4):1005 －1011.］

［3］ 刘滔，何兆伟，赵育善.持续推力时间最优轨道机动问题的改进鲁棒算法［J］.宇航学报，2008，29(4):1216－1221.［Liu Tao，He Zhao-wei，Zhao Yu-shan.Continuous-thrust orbit maneuver optimization using modified robust algorithm［J］.Journal of Astronautics，2008，29(4):1216 －1221.］

［4］ Igarashi J，Spencer D B.Optimal continous thrust orbit transfer using evolutionary algorithms［J］.Journal of Guidance，Control，and Dynamics，2005，28(3):547 －549.

［5］ Pontani M，Conway B A.Particle swarm optimization applied to space trajectories［J］. Journal of Guidance， Control， and Dynamics，2010，33(5):1429 －1441.

［6］ Lee D H，Bang H C.Efficient initial costates estimation for optimal spiral orbit transfer trajectories design［J］.Journal of Guidance，Control，and Dynamics，2009，32(6):1943 －1947.

［7］ Jamison B R，Coverstone V.Analytical study of the primer vector and orbit transfer switching function［J］.Journal of Guidance，Control，and Dynamics，2010，33(1):235 －245.

［8］ Bombrun A，Pomet J B.Asymptotic behavior of time optimal orbital transfer for low thrust 2-body control system［J］.Discrete and Continuous Dynamical Systems，2007(Supplement):122 －129.

［9］ Haberkorn T，Martinon P，Gergaud J.Low-thrust minimum-fuel orbital transfer:a homotopic approach［J］.Journal of Guidance，Control，and Dynamics，2004，27(6):1046 －1060.

［10］ Caillau J，Gergaud J，Noailles J.3D geosynchronous transfer of a satellite:continuation on the thrust［J］.Journal of Optimization theory and Applications，2003，118(3):541 －565.

［11］ Jiang F H，Baoyin H X，Li J F.Practical techniques for lowthrust trajectory optimization with homotopic approach［J］.Journal of Guidance，Control，and Dynamics，2012，35(1):245－258.

［12］ Haykin S.Kalman Filtering and neural networks［M］.USA:John Wiley＆ Sons Inc，2002.