自平衡控制系统稳定性分析与验证

张 毅，张 磊，罗 元

(重庆邮电大学智能系统及机器人研究所，重庆400065)

0 引言

自平衡控制系统的主要任务是精确地获取系统当前准确的倾角及实时产生合适的控制量，使系统维持在平衡状态。由于自平衡控制系统自身的优点，广泛应用在火箭发射中的垂直度控制、倒立摆控制，两足行走机器人以及两轮电动双轮车直立控制等方面，因此，对其稳定的研究具有重要意义［1］。

对于自平衡控制系统，主要任务是准确获取当前系统的倾角，采取一定的策略快速地调节系统保持稳定。通常对自平衡系统的理论及稳定性分析比较复杂，在系统倾角获取上一般采用卡尔曼滤波、互补滤波等算法获取系统当前的倾角数据［2］，但误差仍然存在。对于后续系统平衡的控制，一般采用模糊比例积分微分(proportion integral differential，PID)控制、线性二次型调节器或自适应控制器等方法控制系统达到并维持平衡状态 。为提高控制精度，部分算法需细分控制范围，但会导致控制规则呈几何级数增加，即所谓的“规则爆炸”问题［4］，影响控制实时性。

本文针对自平衡系统采用重心运动方程来分析系统的稳定性及维持系统稳定的控制方法，通过实际和理论分析，降低维持系统稳定性分析和算法的复杂性，同时根据所用的获取倾角数据的方案，配合理论分析与校正得到当前更精确的倾角数据。同时为完成对系统平衡的调节，用滤波后的倾角和陀螺仪数据分别配以对应的参量，组成比例微分(proportion differential，PD)控制，计算出驱动机构的控制量，完成系统的调节过程。

1 数学模型的建立及简化

根据自平衡控制系统的定义与应用场合，其行为特性与倒立摆有很大的相似性［5］，故在分析自平衡控制系统的特性时可以参考对倒立摆稳定性分析的控制方法。但相比于倒立摆，自平衡控制系统有其自身的特点，由于其调整平衡机构的质量相对于整个系统的质量很小，在分析过程中可以忽略驱动机构的质量，这样不但简化了理论分析，而且简化算法的设计，降低控制系统运算的复杂程度。下面将对比倒立摆的建模，引出自平衡控制系统的建模，如图1所示。

图1 倒立摆的受力分析Fig.1 Stress analysis for Inverted Pendulum

图1中，对其水平和垂直方向受力分析、结合刚体动力学方程可得出倒立摆的运动方程［6］:

(1)-(2)式中:x为小车的相对基准位移;x˙为小车的速度;x为小车的加速度;θ为摆线对垂线的角位移;˙θ为摆线对垂线的角速度;¨θ为摆线对垂线的角加速度;J为摆绕其重心的转动惯量;m为摆的质量;M为小车的质量;l为摆重心到转轴之长;H为小车对摆的水平反力;V为小车对摆的垂直反力;c为摆转动时的摩擦系数;b为小车的滑动系数;F为作用在小车上的外力。

由传统的对自平衡系统的分析方法可知，其分析方法复杂，运算求解时间长，为此特简化自平衡系统，降低分析的复杂度。忽略驱动机构的质量M，简化后的倒立摆模型，即等效的自平衡控制系统模型如图2所示，对模型受力分析如图3所示。

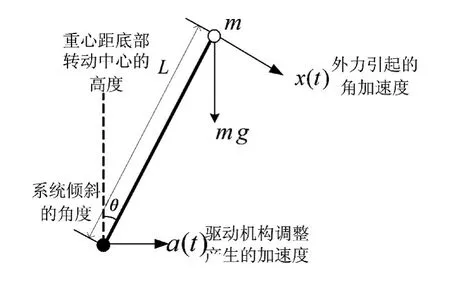
图2 自平衡控制系统等效图Fig.2 Equivalent chart for self-balancing control system

图3 自平衡控制系统受力分析图Fig.3 Stress analysis for self-balancing control system

将模型等效为可绕底部支点左右转动的倒立摆，其重心距底部距离为L，质量为m。假设由于外力的干扰引起系统向右倾斜产生角加速度x(t)，偏离数值方向一个角度θ，忽略驱动机构的质量，控制系统检测到此倾角后立即控制驱动机构驱动底部支点向右加速运动，此时，在质心m所在位置进行分析，它就会受到额外的惯性力，该力作用在系统质心上，与底部驱动调节的加速度方向相反，大小为macosθ，且与a成正比，故在质心m运动的速度方向上。

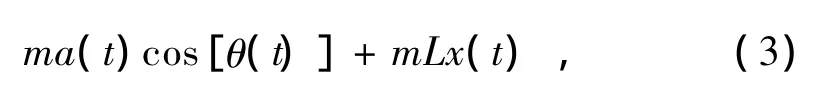
等式两边消去m，得

在实际调节过程中，调节速度很快，通常偏离平衡位置很小角度，故运动方程简化为

2 稳定性分析与极点配置

2.1 实际模型稳定性分析

自平衡控制系统是一个高阶次、非线性、不稳定的系统，在实际的单摆模型中，当物体偏离平衡位置时，受到回复力(重力的切向分力)与物体的位移方向呈钝角α，故单摆在偏离平衡位置时，重力的切向分力对摆动物体做负功，同时由于空气阻力及其它因素，最终使摆动物体停止在平衡位置。而对于自平衡控制系统，其重心在支撑点之上，重心位于支撑点正上方时，系统处于不稳定的平衡状态，由于制造误差和其他外界干扰因素的存在，物体很难停止在支撑点的正上方，一旦偏离支撑点的正上方，摆动物体重力的切向分量与其位移s呈锐角β，即对脱离正上方支撑点的物体做正功，加速摆动物体的偏离程度。2种状态分别如图4和图5所示。

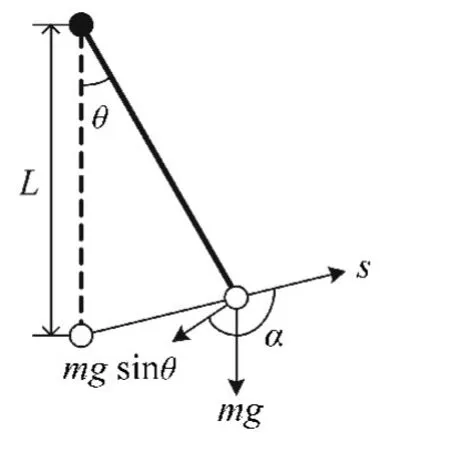
图4 单摆稳定性分析示意图Fig.4 Schematic diagram for stability of pendulum

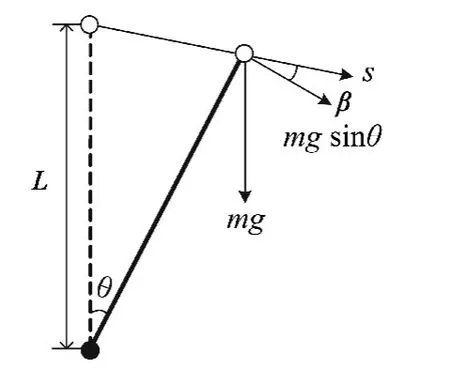
图5 倒立摆稳定性分析示意图Fig.5 Schematic diagram for stability of Inverted pendulum

2.2 系统极点配置

由公式(5)，当自平衡系统静止时，a(t)=0，化简得

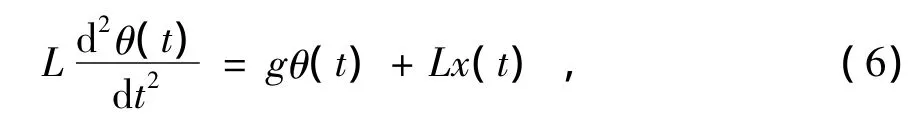
系统传递函数为

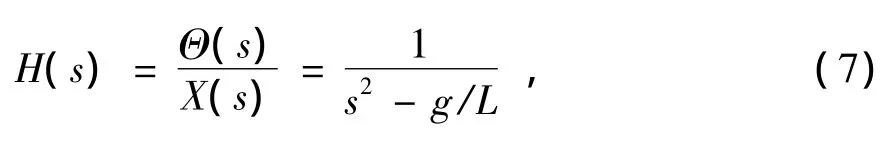
驱动机构通过调节底部支点加减速运动来完成调节平衡的过程。驱动机构进行调节时，系统会在摆动的质心处就会受到额外的惯性力，该力与底部调节机构运动的加速度方向相反，大小成正比(见图3)，此时摆动质心处受到的回复力为

在实际的调节过程中，调节速度很快，通常偏离平衡位置角度很小，故对运动方程线性化为

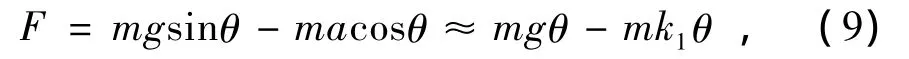
由(8)式，如果k1＞g，回复力的方向便与位移方向相反，当物体偏离平衡位置时，受到指向平衡位置的回复力，使系统重心趋于平衡位置。

为使系统尽快在平衡位置稳定下来，还需增加阻尼力。增加的阻尼力与偏角的速度成正比，方向相反。因此，(8)式变为

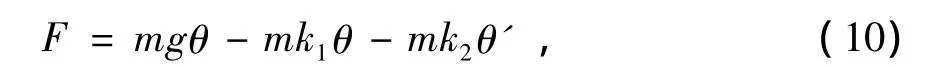
增加阻尼项后，把倒立摆模型等效成单摆模型，能够稳定在平衡位置附近。因此，可得到控制系统的加速度控制算法。

(8)-(11)式中:θ为偏离平衡位置的倾角;θ'为角速度;k1，k2为比例系数。两项相加后作为系统调节平衡的控制量。只要保证k1＞g，k2＞0的条件下，可以使得自平衡系统像单摆一样维持在近似直立的状态。k2决定了回到平衡位置的阻尼系数，选取合适的阻尼系数可以保证系统尽快稳定在平衡位置;k1决定了系统是否能够稳定到垂直平衡位置，它必须大于重力加速度。

得出自平衡控制系统保持稳定性的条件和控制系统的加速度控制算法后，对控制系统引入比例、微分反馈控制，如图6所示。

在图6中，引入了角度反馈控制，与角度成比例的控制量为比例控制;与角速度成比例的控制量为微分控制。其中，微分参数相当于阻尼力，可以有效抑制系统的震荡。引入比例、微分控制后系统稳定性分析如下。

系统的传递函数为

此时，系统的极点为

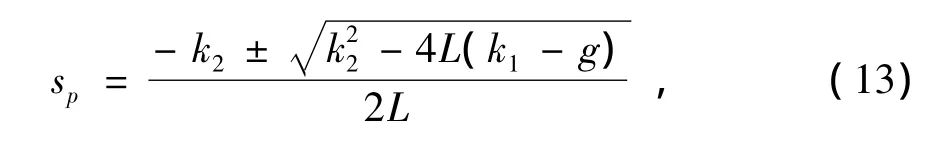
系统要保持稳定，2个极点都位于S平面的左半平面［7］。要满足条件，需要k1＞g，k2＞0。因此，当k1＞g，k2＞0时，自平衡控制系统便可以保持平衡的状态。在实际测试中通过适当调整比例和微分的系数，可使系统快速回到平衡位置，并维持稳定状态。

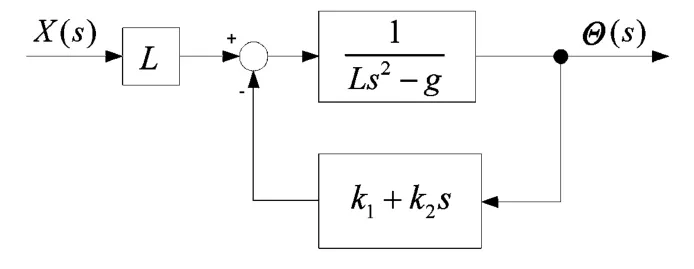
图6 引入比例、微分反馈后的系统框图Fig.6 System block diagram for the introduction of proportional，differential

3 控制策略及结果分析

3.1 获取与处理倾角信息

对自平衡系统稳定性的分析，有助于采用合理控制策略对系统稳定性的控制。由于实际自平衡系统的振动及硬件电路的干扰，会对加速度传感器信号的输出产生很大的干扰。陀螺仪动态性能很好，不易受振动和速度的影响，但容易产生漂移误差，很小误差经过积分运算后会产生很大误差，因此，都不适合单独使用。结合各自的优缺点及系统调解平衡所需的条件，同时采用2种传感器，经过算法处理共同完成角度检测和产生控制量的任务。

为精确获取传感器输出的角度信息，采用卡尔曼滤波对传感器输出的数据进行处理。在应用卡尔曼滤波算法过程中，先对陀螺仪输出的角速度信息进行积分，求得陀螺仪传感器对应的角度信息Angle_gyro:

(14)式中，Gyro_data为陀螺仪输出的角速度信息，对比加速度传感器输出的角度信息，求得当前的角度误差为

(15)式中:Angle－error为当前的角度误差;Angle_data是加速度传感器输出的经过计算的角度信息，依据卡尔曼滤波的第3个公式，并进行简化得

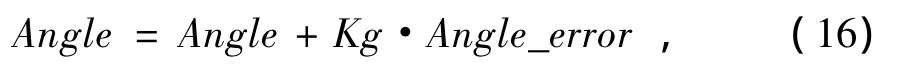
(16)式中，等号左边的Angle就是经过运算之后当前比较准确的角度信息，等式右边的Angle是上一次经过卡尔曼滤波后比较准确的角度信息。在整个卡尔曼滤波运算过程中，需要不断递推卡尔曼增益Kg以及当前的协方差P，以便进行下一次角度的计算和更新。同时也要更新b，求得当前的、经过滤波后的真实角速度Gyro_real，具体控制过程如图7所示。

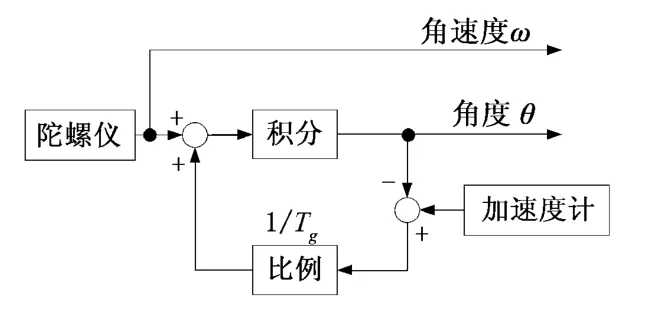
图7 传感器信息处理方法Fig.7 Processing method of Sensor information

利用加速度传感器所获得的角度数据Angle_data，与陀螺仪积分之后的角度Angle_gyro进行比较，将比较的误差经过比例1/Tg放大之后与陀螺仪输出的角速度数据叠加，抵消陀螺仪的积分误差，之后再进行积分，此时获取的角度更接近真实的系统倾角。

3.2 产生控制量

由系统稳定性分析与极点配置，系统快速回到平衡位置并维持稳定需引入比例和微分控制。通过系统对倾角信息的获取及处理，已得到精确的角度和角速度信息。在数学运算关系上，对角度微分得到角速度。系统通过获取传感器的信息并处理，分别得到精确的角度和角速度信息，角度信息看成是比例项的一部分，则获取的角速度信息为微分项的一部分，二者配合适当的系数组成比例微分PD控制器，便可以产生恰当的控制量，控制驱动机构完成调解过程。具体控制过程如图8所示。

图8中，k1和k2分别是比例系数和微分系数，具体意义和功能上面已论述，产生控制量的表达式为

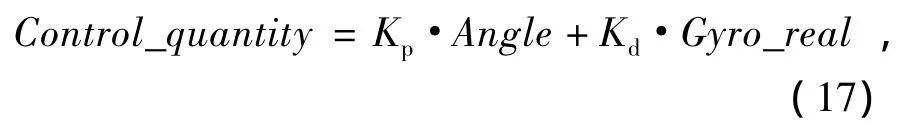
(17)式中，Kp和Kd相当于图8中的k1和k2。适当的调节Kp和Kd，便可得到合适的控制量，控制驱动机构完成平衡的调整。

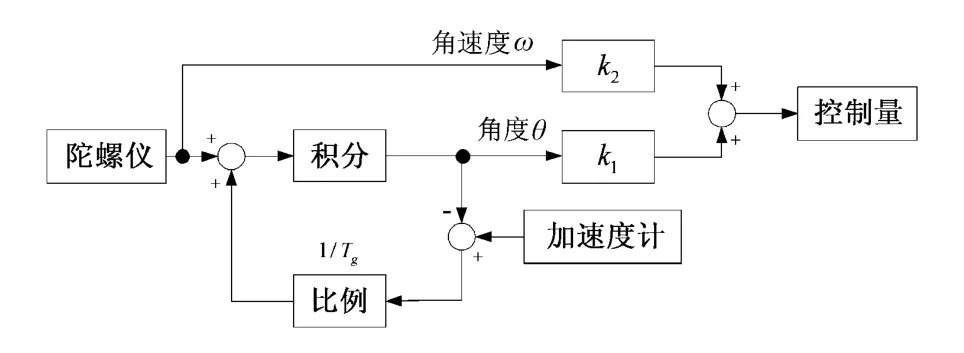
图8 产生控制量的方法Fig.8 Method for generating control quantity

3.3 测试结果及分析

在测试平台上搭建自平衡控制系统，精确获取系统角度和角速度信息，适当调节控制量相关的参数，便可完成对自平衡系统稳定性的控制。将自平衡控制系统运行中的参数实时传送到上位机，便可观察各参数之间的变化，滤波前的角度与滤波后的角度各放大1 000倍后对比如图9所示。

图9 滤波前后的角度对比Fig.9 Angle Contrast before and after filtering

图9中，下方曲线是滤波前的角度数据，上方曲线是经过滤波和误差比较放大后的角度数据。从图9中可知，由于机械振动对加速度输出的影响及硬件电路电磁干扰的存在，滤波前采集到的角度数据混有高频干扰信号，经过滤波后，角度数据比较光滑，更为接近实际的角度数据。

系统调节产生的控制量需要当前比较准确的角度数据和角速度数据，故需对采集的角度和角速度数据进行滤波，获得相对精确的数据。各放大1 000倍后上传到上位机，图10为滤波前后角度波形与滤波后陀螺仪数据变化情况，中间2条频率比较低的波形为滤波前后的角度数据，位置关系见图9。频率和幅值比较高的曲线是滤波后陀螺仪波形。

滤波后的角度、角速度与控制量之间的波形如图11所示。图11中，角度数据放大100倍，陀螺仪数据放大10倍，控制量不放大。其中，处于上方频率较低的波形为滤波后的角度数据，中间频率比较低的波形为产生的控制量，下方的频率和幅值比较高的波形为滤波后的陀螺仪数据。由图11可知，由PD控制器产生控制量波形与角度数据波形比较相近，主要原因是角度数据在控制量的产生中占有很大的比重。

图10 滤波前后角度和角速度波形Fig.10 Angle and angular velocity before and after filtering

图11 滤波后的角度、角速度与控制量之间的波形Fig.11 Waveform of angle，angular velocity and control quantity after filtering

4 结束语

本文从理论和实际2个方面对自平衡控制系统的稳定性进行分析，依据理论和实际的分析结果，推导出维持系统保持稳定性所需的条件。设计了自平衡控制系统测试平台，在测试平台上进行算法和改进控制策略的验证。通过测试，系统能很好地完成倾角数据的处理，调节系统处于平衡状态，同时，将系统获得的角度、角速度及相关的控制量数据实时传送到上位机，生成波形图，方便了解各参量之间的关系。

［1］屠运武，徐俊艳，张培仁，等.自平衡控制系统的建模与仿真［J］.系统仿真学报，2004，16(4):839-841.TU Yunwu，XU Junyan，ZHANG Peiren，et al.Model and Simulation of Self-balance Control System［J］.Jour-nal of system simulation，2004，16(4):839-841.

［2］肖乐.两轮自平衡机器人建模及智能控制研究［D］.哈尔滨:哈尔滨理工大学，2011:5-14.XIAO Le.Two-wheel Self-balancing Robot Modeling and Intelligent Control［D］.Harbin:Harbin University of Science and Technology，2011:5-14.

［3］孙建勤.两轮自平衡小车大范围镇定方法研究［D］.西安:西安电子科技大学，2010:34-54.SUN Jianqin.Research on Methods of the Two-wheeled Self-balancing Vehicle’s Wide-range Stability［D］.Xi an:Xidian University，2010:34-54.

［4］YONG T K，BIEN Zeungnam.Robust self-learning fuzzy controller design for a class of nonlinear MIMO systems［J］.Fuzzy Sets and Systems，2000，111(2):117-135.

［5］HYUNGJIK L，SEUL J.Balancing and navigation control of a mobile inverted pendulum robot using sensor fusion of low cost sensors［J］.Mechatronics，2012(2):95-105.

［6］SHIROMA N，MATSUMOTO O，KAJITA S，et al.Cooperative behavior of a wheeled inverted pendulum for object transportation［C］//Proceedings of the 1996 IEEE/RSJ International Conference on.Intelligent Robots and Systems.Japan，Osaka:IEEE Press，1996，2:396-401.

［7］胡寿松.自动控制原理［M］.4版.北京:科学出版社，2007.HU Shousong.Automatic control theory［M］.4th Edition.Beijing:Science Press，2007.

［8］SPONG M W，CORKE P，LOZANO R.Nonlinear control of the reaction wheel pendulum［J］.Automatica，2001，37(11):1845-1851.