耦合三端子量子点系统中Andreev反射调控的热电输运

郝方原，王瑞强

(华南师范大学物理与电信工程学院 广东省量子工程与材料重点实验室，广州510006)

热电效应(即Seebeck 效应)是指在存在温度梯度情况下电子由高温区向低温区移动，导致电荷堆积的一种现象. Seebeck 效应是温差发电的基础，当前全球环境和能源条件恶化的情况下，利用热电效应原理的温差发电技术已成为引人注目的研究领域.另一方面，随着自旋电子学的发展，也促进了自旋电子器件的研发.然而，在自旋电子学的发展过程中遇到许多技术难题，最大的难题之一就是自旋流的产生问题. 2008年，日本著名研究小组Uchida等［1］将热电效应与自旋电子学相结合，提出了类似于电荷Seebeck 效应的一个新的概念——自旋Seebeck 效应.在磁性材料N81Fe19薄膜的热电实验中，测量出由温度梯度产生的自旋偏压，即首次得到自旋相关的Seebeck 效应. 该成果标志着自旋偏压或自旋电流的产生可以由热电效应机制来实现，为自旋流的产生提供了新方法，由此极大地激发了这方面的研究.在单分子磁性体(SMM)的热电效应研究中［2－4］，通过调控门电压，可以获得纯的自旋流，其特点是自旋热电系数大于电荷热电系数. 在单量子点热电输运的研究中［5］，发现自旋极化的热电流有明显的重整化效应. 总之，纳米材料的热电输运的研究不仅有助于理解纳米结构中热电输运重要的物理机制，还为产生、调控、检测自旋提供新颖的方法.

在纳米结构体系中，将量子点耦合到电极的混杂系统成为研究热点，因为该体系中电子输运可通过耦合电极来控制. 将量子点耦合到包括超导材料的多端子混杂体系时，超导电极的引入使得系统包含更丰富的物理机制. 在超导体中，一个自旋向上(向下)的电荷与其自旋相反的电荷以库伯对(Cooper pair)的形式参与输运过程. 在该混合系统中，如果自旋相反的2个电子来自于同一个电极，则发生所谓的正常Andreev 反射;如果2个电子来自于不同的电极，则发生交叉Andreev 反射. 由于Andreev 反射中电子的配对是自旋相关的，如果同时引入铁磁电极和超导电极，那么系统将表现出更多新奇的现象.例如，在铁磁电极上加偏压，则在正常金属电极端能产生自旋极化的电流，甚至是纯的自旋流［6］;通过对混合系统中电子输运特性的研究，可以辨别和分析交叉的Andreev 反射［7］，这对深入理解超导体的物理机制具有重要作用.

关于多端子量子点系统的研究，主要集中于外加偏压驱动下电子的输运，而对热电输运却涉及很少.最近研究发现，多端子系统的热电效应能呈现出很多有趣的现象.当1个量子点耦合2个铁磁电极及1个正常金属电极时，在偏温的条件下，在正常金属电极端能产生纯的自旋流［8］. 当多端子系统中引入超导电极时，发现自旋热电系数及电荷热电系数可以达到很大，并且门电压和温度对自旋热电系数和电荷热电系数有显著的影响［9］. 本文以1个三端子量子点混杂系统为研究对象，在铁磁电极和正常电极之间施加一个温度差，采用Master 方程计算方法，得出了正常金属电极端的热电荷流和热自旋流的表达式，并重点讨论超导电极对电荷流及自旋流的影响.

1 理论模型

一个量子点耦合到超导金属电极(S)、铁磁金属电极(F)和正常金属电极(N)的三端子混杂系统(图1).

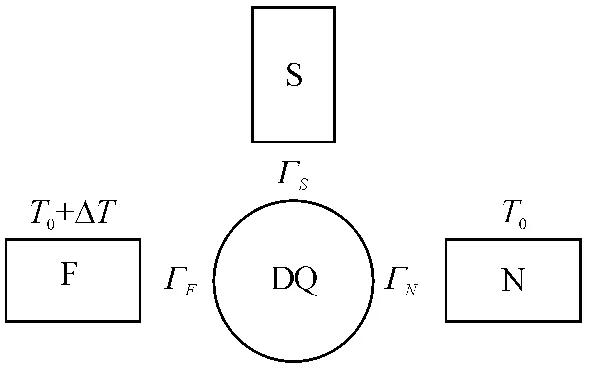
图1 三端子示意图Figure 1 Schematic model of a three-terminal

该系统的哈密顿量表示如下:

式中，Hdot为量子点的哈密顿量，Hα(α =F，N，S)为不同电极的哈密顿量，Hαt表示电子在量子点与电极α 之间的隧穿哈密顿量. 铁磁电极、正常电极、超导电极的哈密顿量分别表示如下:

式中第一项描述了电极上无相互作用的电子，其中H.c.表示，其能量εαkσ是与动量k 和自旋有关是电子的产生(湮灭)算符.第二项中aα－k↓aαk↑表示BCS 理论中的超导库伯对，Δ表示库伯对的对势能，当α = S 时，此项不为零. 采用安德森模型，量子点的哈密顿量可以表示为:

Vα为自旋无关的隧穿矩阵元，H.c.表示为了简化，在宽带近似下认为该矩阵元与动量无关.由此导致的隧穿耦合强度定义为:

其中ρασ表示在电极α 上自旋为σ 的电子态密度.当耦合电极为铁磁电极时，引入自旋极化强度p =(ρF↑－ρF↓)/(ρF↑+ρF↓)来表示其磁性的强弱，则相关的隧穿耦合强度ΓF，↑(↓)=ΓF(1 ±p).

2 研究方法

为了研究Andreev 反射对热电输运特性的影响，考虑一种极限情况Δ→∞，这时超导中的准粒子激发受到严重的抑制.在此条件下，与超导电极耦合的量子点可以用1个有效的哈密顿量［10－12］表示:

考虑量子点弱耦合到非超导电极的情况，即铁磁电极的耦合强度ΓF. 正常金属电极的耦合强度ΓN小于kBT.在此条件下，整个系统的动力学行为可以用密度矩阵所满足的刘维尔运动方程来描述，在玻恩近似和马尔可夫(Markovian)近似下，可以得到一套关于密度矩阵的量子Master 方程［13］:

这里，Pi是密度矩阵的对角元，代表t 时刻找到量子点在占据态的几率;

由式(9)计算Pi之后，进一步计算出电极α 上自旋为σ 的电流，其计算公式为:

3 结果与讨论

将铁磁电极端的温度设置为TF=T0+ΔT，正常金属电极端的温度设置为TN=T0. 为了简单，仅考虑对称耦合的情况，即ΓF=ΓN↑=ΓN↓=Γ0. 以U为能量单位，具体参数设置为T0=0，kBΔT =0.05，Γ0=0. 01，p =0. 6 以及μS=0. 利用式(9)和式(10)，可以计算得到正常金属端的自旋流，其表达式如下:

而通过正常金属极端的电荷流为:

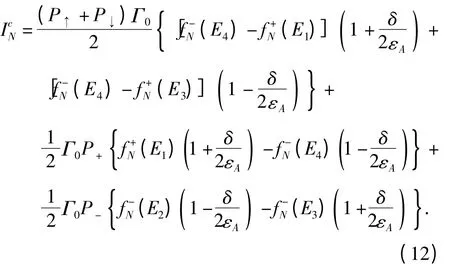
式(11)和式(12)中，简记E1=U/2 +εA，E2=U/2－εA，E3=－U/2 +εA，E4=－U/2－εA，表示量子点中单占据态与空态和双占据态或之间跃迁时的激发能.

当该混合系统不受超导电极的影响时(ΓS=0)，系统退化为简单的铁磁/量子点/正常金属隧道结系统.一个明显的现象就是通过调节量子点能级ε，电流的方向可以从正到负改变，这是偏温驱动情况下特有的性质［2］，主要来源于在不同量子点能级下，或者电子或者空穴在输运中占主导的表现，这明显区别于偏压驱动下电流方向固定的情况. 比较正常金属极中电荷流和自旋流曲线可知，它们有类似的变化行为，都在ε=0 及ε =－U 左右呈现出2个符号相反的峰值，这是电子型输运与空穴型载流子输运的转换点. 在粒子－空穴对称点ε =－U/2 附近，出现了一个零电流的平台，电荷流和自旋流关于ε=－U/2 严格反对称.当ΓS≠0 时，无论是还是的峰值都对超导的耦合强度ΓS非常敏感.随着ΓS逐渐增大，一方面电流峰值被压抑而变小，另一方面处于位置ε=0 和ε =－U 的峰值以ε=－U/2 为中心逐渐靠拢.可以解释为:当ΓS为有限时，量子点中量子态或发生跃迁所需要的激发能要发生修正，在图2中，2个峰值转换点的位置分别处于ε1= (－ U－是由E1=0 及E2=0 所决定.由此可见，当ΓS增大时，ε1处的峰值向右移而ε2处的峰值向左移. 另外，从式(11)和式(12)可以看出，ΓS也严重影响着电流计算公式中隧穿强度，当ΓS增大时，εA也增大，导致电流的减小.超导电极对正常金属电极或的影响，可以用来调控热电效应的电流大小及其方向.

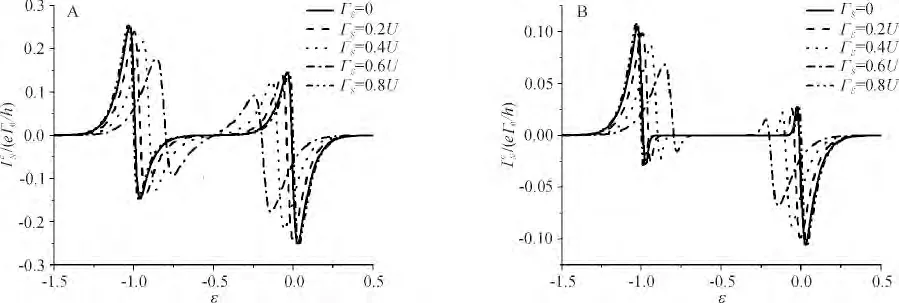
图2 正常金属电极中热电荷流(A)和热自旋流(B)随门电压的变化关系Figure 2 Thermal charge current (A)and thermal spin current (B)in normal lead as a function of dot level

图3 正常金属电极中热电荷流(A)和热自旋流(B)随超导电极耦合强度ΓS 的依赖关系Figure 3 Thermal charge current (A)and thermal spin current (B)in normal lead as a function of ΓS

4 结论

通过对耦合到一个超导电极、一个铁磁电极和一个正常金属电极的三端子量子点混杂系统的研究，不仅有助于理解在纳米结构中耦合了超导电极的混杂系统的热电输运性质和物理机制，还为产生、调控、检测自旋提供一个新颖的方法. 利用量子Master 方程推导出热自旋流和热电荷流表达式. 绘制出了混杂系统热自旋流和热电荷流受门电压和超导电极影响，利用Andreev 反射机制，重点讨论了在偏温条件下超导电极对混合系统产生的热电荷流和热自旋流的调控作用，这对深入理解超导体的物理机制具有一定的作用.

［1］Uchid A K，Takahashi S，Harii K，et al. Observation of the spin Seebeck effect［J］.Nature，2008，455(7):778－781.

［2］Wang R Q，Sheng L，Shen R，et al. Thermoelectric effect in single-molecule-magnet junctions［J］. Physical Review Letters，2010，105(5):057202.

［3］Zhang Z Z，Liang J，Wang R Q，et al. Thermoelectricinduced spin currents in single-molecule magnet tunnel junctions［J］. Applied Physics Letters，2010，97(24):242101.

［4］王瑞强，刘晨. 量子点隧道结中自旋相关的电流关联［J］.华南师范大学学报:自然科学，2011(4):71－74.Wang R Q，Liu C. Spin-dependent current correlation in quantum dot tunnel junction.［J］.Journal of South China Normal University:Natural Science Edition，2011(4):71－74.

［5］Qi F H，Ying Y B，Jin G J. Temperature-manipulated spin transport through a quantum dot transistor［J］. Physical Review B，2011，83(7):075310.

［6］Futterer D，Governale M，Köing J. Generation of pure spin currents by superconducting proximity effect in quantum dots［J］.Europhysics Letters，2010，91(4):47004－47010.

［7］Futterer D，Governale M，Pala M G，et al. Nonlocal Andreev transport through an interacting quantum dot［J］.Physical Review B，2009，79(5):054505.

［8］Ying Y B，Jin G J. Nonlocal tunnel magnetoresistance and thermal rectification effect in a nanoscale three-terminal junction［J］. Journal of Physics:Condensed Matter，2012，24(49):495304.

［9］Wysoki ski K I. Thermoelectric transport in the three terminal quantum dot［J］.Journal of Physics:Condensed Matter，2012，24(33):335303.

［10］Rozhkov A V，Arovas D P. Interacting-impurity Josephson junction:Variational wave functions and slave-boson mean-field theory［J］. Physical Review B，2000，62(10):6687－6691.

［11］Karrasch C，Oguri A，Meden V. Josephson current through a single Anderson impurity coupled to BCS leads［J］. Physical Review B，2008，77(2):024517.

［12］Meng T，Florens S. Self-consistent description of Andreev bound states in Josephson quantum dot devices［J］.Physical Review B，2009，79(22):224521.

［13］Timm C. Tunneling through molecules and quantum dots:Master-equation approaches ［J］. Physical Review B，2008，77(19):195416.