代数体函数与其系数函数的Borel点

孙道椿 ，张少华，吴昭君，郭晓晶

(1.华南师范大学数学科学学院，广州510631;2.湖北科技学院数学与统计学院，咸宁437100;3.广州大学松田学院，广州511370)

本文首先研究了单位圆内的k 值代数体函数，证明了一些单位圆内的定理. 然后利用这些定理首次研究了确定代数体函数的系数函数的Borel 点与代数体函数的Borel 点间的关系. 本文使用的术语和符号与文献［1］－［10］相同.

设Ak(z)，Ak－1(z)，…，A0(z)是连通区域D 内一组没有公共零点的解析函数，则二元复方程

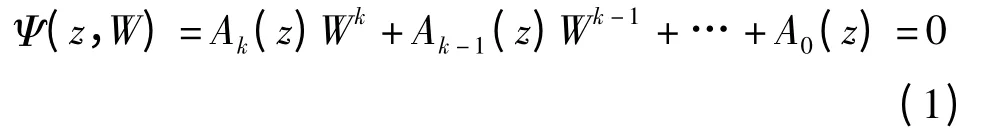
定义了区域D 上的一个k 值代数体函数W(z). 若Ψ(z，W)在D 上是不可约的，则称W(z)是D 上的不可约k 值代数体函数. 本文一般不要求代数体函数是不可约的. 若Ak(z)≡1，则称W(z)是D 上的k值整代数体函数.若Ak(z)，…，A0(z)都是D 上的多项式，则称W(z)是D 上的k 值代数函数.

用经过所有分支点的曲线将圆盘{|z| ＜R}割开成单连通区域D－，W(z)在D－上分离成k个单值分支，记为定义

定理1 设W(z)= {(wt(z)，a)}，M(z)={(mt(z)，a)}是{|z| ＜R}上2个有对应关系的k 值代数体函数.则对任意r(0，R)，有

为了建立圆盘内代数体函数的Nevanlinna 第一基本定理，给出如下引理.

引理1 设f(z)和g(z)是圆盘{|z| ＜R}上2个不恒为零、也不恒为无穷的亚纯函数，对任意r(0，R)，有

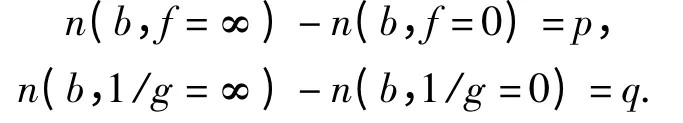
则在b 点附近有

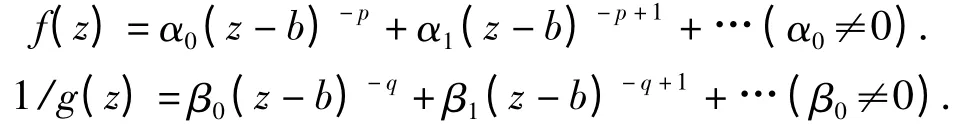
因此

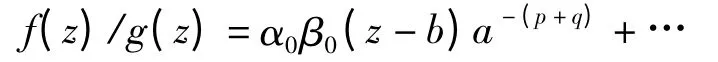
当p+q≥0 时，n(b，f/g=∞)=p+q，n(b，f/g =0)=0.当p+q ＜0 时，n(b，f/g =∞)=0，n(b，f/g =0)=－p－q. 所以

定理2 (代数体函数的Jensen 公式)设W(z)是圆盘G={|z| ＜R}内由二元复方程

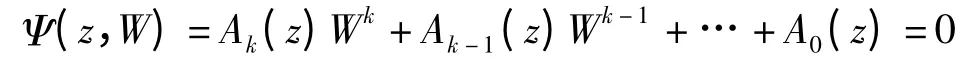
定义的k 值代数体函数.

i)若A0(z)=Ψ(z，0)≢0，则其中ak是亚纯函数在原点罗朗展式中第一个非零系数.

ii)若Ψ(z，b)≢0，则

其中cb是亚纯函数Ψ(z，b)/Ak(z)在b 点罗朗展式中第一个非零系数.

证明 用经过所有分支点的曲线将圆盘G 割开成单连通区域D－，设{Wj(z)}是D－上分离W(z)得到的k个单值分支.

上面第2个等式用到了引理1，并注意N(r，A0(z)=∞)=0 =N(r，Ak(z)=∞).

ii)令M=W－b，则二元复方程

定义一个k 值代数体函数M(z). 注意Ψb(z，0)≡Ψ(z，b)≡B0(z)，对M(z)应用i)即得ii).

定理3 (Nevanlinna 第一基本定理)设W(z)是圆盘{|z| ＜R}上由二元复方程(1)定义的k 值代数体函数. 设bC，Ψ(z，b)≢0，则有

其中cb是Ψ(z，b)/Ak(z)在原点罗朗展式中第一个非零的系数.

证明 由定理1 知

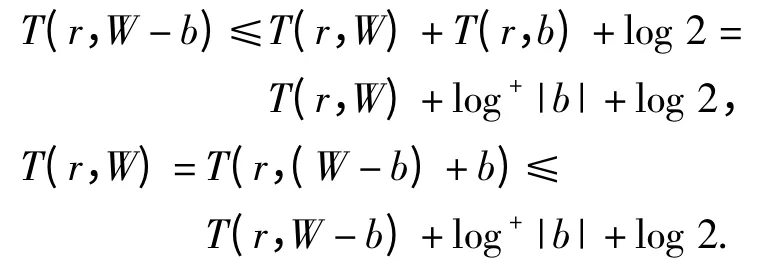
结合二者得

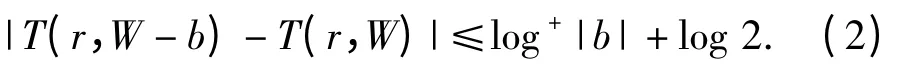
应用定理2 得

代入式(2)就得到定理3.

定理4 设W(z)是圆盘{|z| ＜R+ε}内由二元复方程

定义的k 值整代数体函数. 定义它的最大模函数为

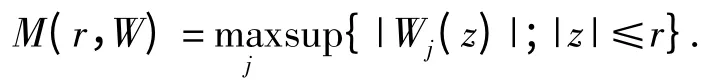
则对任意0 ＜r ＜R，有

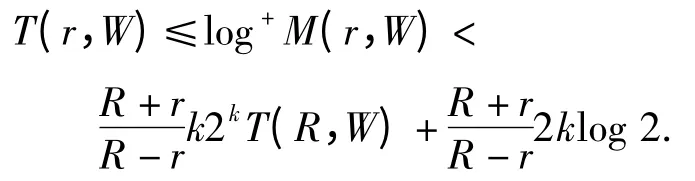
证明 先证明第一个不等式，即

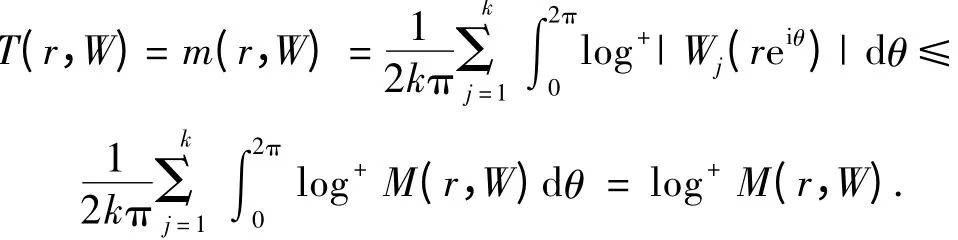
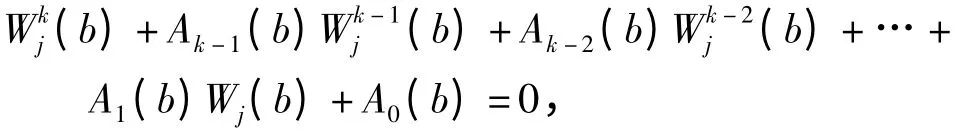
知

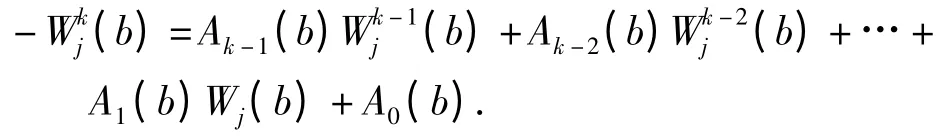
因此

所以

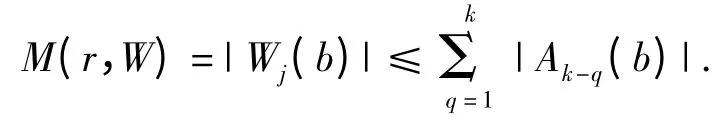
对上式取对数后运用Poisson-Jensen 公式及韦达定理

即

定理4 得证.

注1 关于不可约代数体函数的Jensen 公式和第一基本定理，在文献［2］中均有详细描述，我们这里的证明不要求代数体函数是不可约的. 关于平面上整代数体函数与定理4 对应的结果见文献［4］.

为了确定代数体函数的系数函数的Borel 点与代数体函数的Borel 点之间的关系，我们先研究单位圆内代数体函数的增长级与其系数函数的增长级之间的关系. 文献［4］研究了复平面上的代数体函数的增长级与其系数函数的增长级之间的关系.

定义1 设n(r)是(0，1)上的正值实函数. 定义n(r)的级为

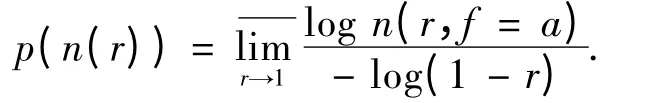
定义T(r，W)的级为单位圆内代数体函数W(z)的级.

设W(z)是单位圆内的k 值整代数体函数. 由定理4 得ρ(W)≤p(log+M(r，W))≤1 + ρ(W).

引理2［10］设n(r)是(0，1)上的正值实函数.若p(n(r))≥1，则有p(n(r))= 1 +p(N(r))，这里

引理3［9］设W(z)是单位圆内由式(1)确定的k - 值代数体函数. 则

其中ck表示Ak(z)在零点的罗朗展式中第一个非零系数，

引理4 设W(z)是单位圆内由式(1)确定的ρ(W)级k－值代数体函数. 则

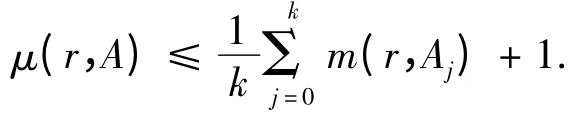
从而有ρ(W)≤ρ(AM))，其中ρ(AM)=max{ρ(At);t=0，1，2，…，k}.

证明 由μ(r，A)的定义有

由此即得引理.

注2 引理4 的反方向的不等式不一定成立.如H(z)=exp{(1/(1－z))2}.注意单位圆内2 值代数体函数H(z)(1－z)W2－H(z)=0 可写成W(z)，故是零级的(ρ(W)=0)，但ρ(A0)

引理5 设W(z)是单位圆内由式(1)确定的ρ(W)级k 值代数体函数.任取t，u{0，1，2，…，k}，若Au(z)≢0，则有

其中|x|+=max{1，x}.则

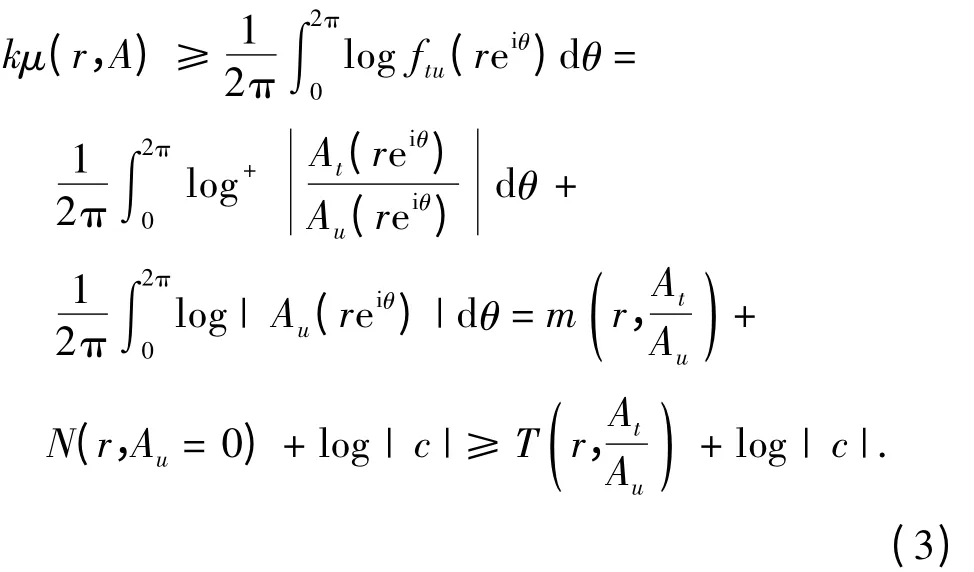
结合引理3 及式(3)，得

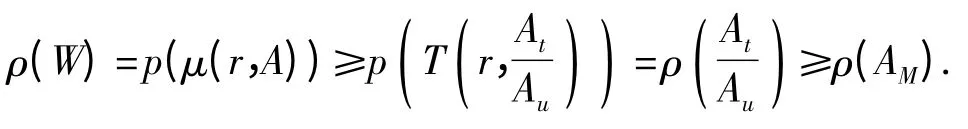
再结合引理4 即得ρ(W)=ρ(AM).

由引理5 立即可得

推论1 W(z)是单位圆内由式(1)确定的ρ(W)级k 值整代数体函数. 则必有ρ(W)=ρ(AM)成立，即ρ(W)=max{ρ(Aj);j=0，1，2，…，k－1}.

引理6 任取ε ＞0，

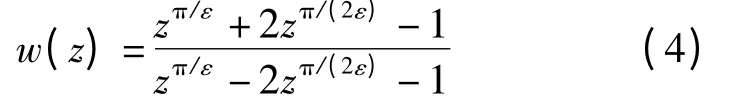
是将扇形{z;0 ＜|z| ＜1}∩{z;|arg z| ＜ε}变到单位圆盘{|w| ＜1}的共形映射.则存在一个仅与ε 有关的常数b(0，1)，使得

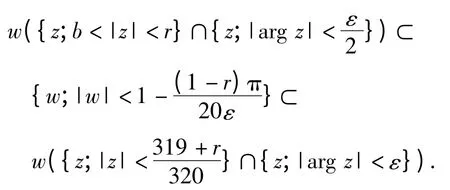
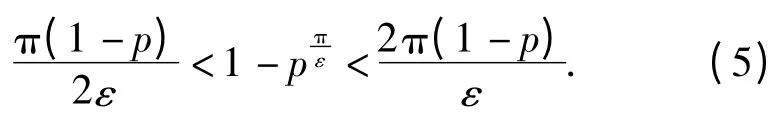
容易验证w(z)是将扇形{z;b ＜|z| ＜1}∩{z;|arg z|＜ε}变到单位圆盘{|w| ＜1}的共形映射，且有记z0=peiφ=pcos φ+ipsin φA，令

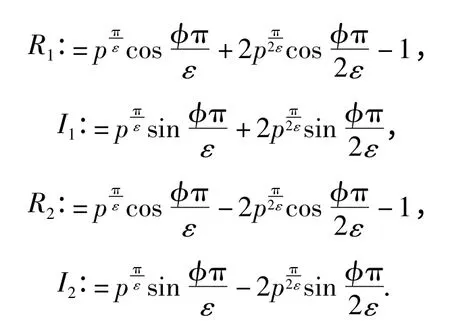
则由式(4)有

又由于

结合式(5)～(7)知

结合式(8)、(9)可得

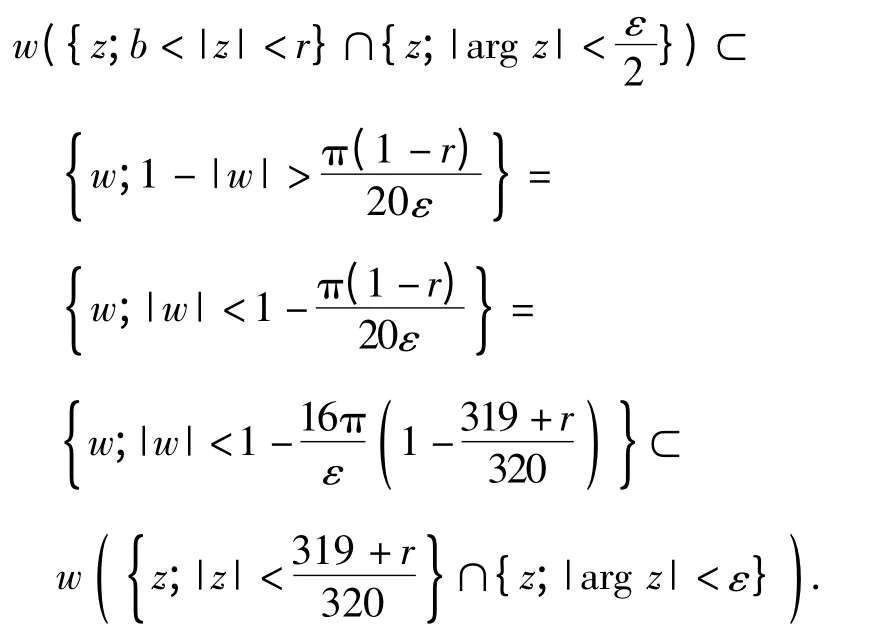
下面研究单位圆内代数体函数的Borel 点和确定代数体函数的系数函数的Borel 点之间的关系.为此，先给出Borel 点的定义.

定义2 设W(z)是单位圆内k 值代数体函数(包括圆内亚纯函数)，若对任意bC∞，至多除去2k个例外(至多有2个例外值)，任意ε ＞0，n(r，t－ε，t +ε，W =b)(表示扇形{z;b ＜|z| ＜r}∩{z;|arg z－t| ＜ε}中W(z)－b 的零点个数)的级恒为p，则称eit是W(z)的p 级Borel 点.若n(r，t－ε，t +ε，W=b)的级至少为p，则称eit是W(z)的至少为p级的Borel 点.

定理5 设W(z)是单位圆内由二元复方程

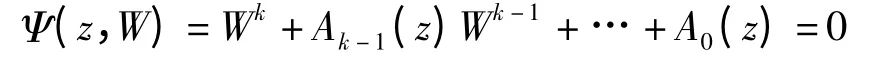
定义的k 值整代数体函数. 设eit是Aj(z)(0≤j≤k－1)的一个p(＞1)级Borel 点，则eit一定是W(z)的一个至少p 级的Borel 点. 特别，若代数体函数是p－1 级的，则eit是W(z)的p 级的Borel 点.

其中n(r，t－ σ，t + σ，Aj(z)= b)= n(r，－ σ，σ，Aj(zeit)=b). 用映射(4)将扇形D:={|z| ＜1}∩{|arg z| ＜ε}变到单位圆B:={|w| ＜1}，其逆映射记为z(w)，由引理6 得

即n(r，Aj(z(w)eit)=b)在单位圆B 内的级至少是p. 由引理2，N(r，Aj(z(w)eit)=b)在B 内的级至少是p－1. 结合亚纯函数的Nevanlinna 第一基本定理，单位圆内解析函数Aj(z(w)eit)的级至少是p－1.由推论1，整代数体函数W(z(w)eit)在单位圆B 内的级至少是p－1 级. 再结合代数体函数的Nevanlinna 第二基本定理及引理2，任取d 不是例外值，则n(r，W(z(w)eit)=d)在单位圆B 内至少是p级.应用引理6 即得

这说明在扇形{|z| ＜1}∩{|arg z| ＜ε}内，n(h，－ε，ε，W(zeit)=d)至少是p 级，即在扇形D:={|z| ＜1}∩{|t－arg z| ＜ε}内，n(h，t－ε，t +ε，W(z)=d)至少是p 级.由d 的任意性，eit是W(z)的至少p 级Borel 点. 若代数体函数是p－1 级的，则eit是W(z)的至多p 级Borel 点.

定理6 设W(z)是单位圆内由二元复方程

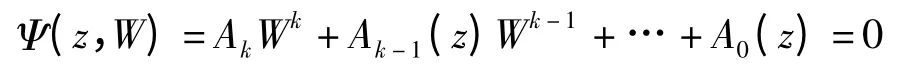
定义的k 值代数体函数.若eit是W(z)的一个p(＞1)级的Borel 点，则至少存在一个正整数j{0，1，2，…，k}，使eit是Aj(z)的一个至少p 级的Borel 点.

类似定理5 的证明，可以证明N(r，W(z(w)eit)=b)在单位圆内的级至少是p－1.由定理3，单位圆内代数体函数W(z(w)eit)的级至少是p－1. 由引理4，至少存在一个正整数j{0，1，2，…，k}，使单位圆内解析函数Aj(z(w)eit)的级至少是p－1.结合亚纯函数的Nevanlinna 第二基本定理及引理2，任取d 不是例外值，则n(r，Aj(z(w)eit)=d)在单位圆B 内至少是p 级.再用引理6 即得

这说明在扇形D:={|z| ＜1}∩{|arg z| ＜ε}内，n(h，－ε，ε，Aj(zeit)=d)至少是p 级，即在扇形D:={|z| ＜1}∩{|t－arg z| ＜ε}内，n(h，t－ε，t +ε，Aj(z)=d)至少是p 级. 由d 的任意性，eit是Aj(z)的至少p 级Borel 点.

定理7 设W(z)是单位圆内由二元复方程

定义的k 值p－1(＞0)级整代数体函数. 则eit是W(z)的p(＞1)级Borel 点的充分必要条件是至少存在一个正整数j{0，1，2，…，k－ 1}，使eit是Aj(z)的一个p(＞1)级Borel 点.

证明 由定理5 得充分性. 下证必要性:设eit是W(z)的p(＞1)级Borel 点，由定理6，存在正整数j{0，1，2，…，k}，使eit是Aj(z)的一个至少p 级的Borel 点. 结合推论1，Aj(z)的级至多是p－1，因此eit至多是Aj(z)的p 级Borel 点.证毕.

［1］杨乐. 值分布论及其新研究［M］.北京:科学出版社，1982.

［2］何育赞，萧修治. 代数体函数与常微分方程［M］. 北京:科学出版社，1988.

［3］孙道椿，高宗升. 代数体函数的唯一性定理［J］.华南师范大学学报:自然科学版，2005(3):80－85.Sun D C，Gao Z S. Uniqueness theorem of algebroidal functions［J］. Journal of South China Normal University:Natural Science Edition，2005(3):80－85.

［4］孙道椿. 代数体函数的增长性［J］. 华南师范大学学报:自然科学版，2006(3):1－6.Sun D C.On the growth of algebroidal functions［J］.Journal of South China Normal University:Natural Science Edition，2006(3):1－6.

［5］王辉坚，孙道椿. 代数体函数的正规定理［J］.华南师范大学学报:自然科学版，2009(2):9－11.Wang H J，Sun D C.Normal theorem of algebroidal functions［J］.Journal of South China Normal University:Natural Science Edition，2009(2):9－11.

［6］孙道椿，郭晓晶. 零点，极点和分支点［J］. 华南师范大学学报:自然科学版，2009(3):1－4.Sun D C，Guo X J. Zeros，poles and branch points［J］.Journal of South China Normal University:Natural Science Edition，2009(3):1－4.

［7］向士东，孙道椿，王松敏. 关于代数体函数的注记［J］.华南师范大学学报:自然科学版，2010(4):5－8.Xiang S D，Sun D C，Wang S M. A note of algebroidal functions［J］. Journal of South China Normal University:Natural Science Edition，2010(4):5－8.

［8］Wu Z J. T－Direction and Borel Direction of algebroid functions of finite and positive order［J］. Georgian Mathematical Journal，2009，16(3):583－596.

［9］Huo Y Y，Sun D C. Algebroid function and its derived function in unit circular disc［J］. Acta Mathematica Scientia，2009，29B(1):129－139.

［10］Sun D C. Commom Borel points of a meromorphic function and its derivatives in the unit circle［J］.Acta Mathematica Scientia，1984，4B(2):227－232.