可渗透反应墙墙体内流速及流态数值模拟

汪 强，徐建平

（安徽工程大学 生物与化学工程学院，安徽 芜湖 241000）

酸性矿井废水（Acid Mine Drainage，简称AMD）是世界采矿工业面临的最具挑战性的环境问题之一.由于煤矿开采过程中，破坏了煤层及围岩中的硫化矿物（主要是硫铁矿）原来的还原环境，使之与氧气和水接触，在微生物作用下发生一系列复杂物理化学反应，生成大量的低p H值废水，该废水又将煤层及围岩中的有毒有害金属离子溶滤其中，形成了酸性矿井废水[1-3].该含有多种有害金属离子的酸性矿井废水的排放，将会导致严重的水体和土壤污染.

可渗透反应墙（PRB）是一种被动的原位修复技术，根据美国环保局1998年发行的《污染物修复的PRB技术》手册定义，PRB技术是指在地下水安装活性材料墙体以便拦截污染物羽状体，使污染羽状体通过反应介质后，其污染物能转化为环境接受的另一种形式，从而实现使污染物浓度达到环境标准的目标.本课题研究由透水的反应介质及固载硫酸盐还原菌组成的新型PRB，将其置于酸性矿井废水的下游，当酸性矿井废水通过PRB时，通过产生沉淀、吸附、氧化还原等物化及生化反应去除水中的污染物，从而得到清洁地下水[4].本文主要采用计算流体力学（CFD）商业软件Fluent对酸性矿井废水流经新型可渗透反应墙进行仿真数值模拟，研究该墙体内水流速度及流态，为墙体内填充介质固定生物菌提供水力学依据.

1 应用Fluent软件原因及基本方程

流体运动的规律都是以质量、动量和能量三大守恒定律等基本物理定律为基础的.而这些基本定律可由数学方程组描述，采用数值计算方法和图像显示对包含有流体流动和热传导等相关物理现象进行分析，该方法即是计算流体力学（CFD）[5-6].该法的优点在于数值模拟可以形象地再现流动情景，没有具体实验带来的经费投入、人力和物力的巨大消耗及周期长等许多困难.因此，要研究可渗透反应墙墙体内流体运动规律可以采用该方法.

近年来，计算流体力学（CFD）发展很快，有许多比较成熟的商业软件包，如Fluent、CFX、StarCD等.而Fluent是目前功能最全面、适用性最广、国内使用最广泛的CFD软件之一[5-6].针对陶粒这一多孔介质材料，Fluent定义的多孔介质的动量方程具有附加的动量源项[7].源项由两部分组成，一部分是粘性损失项（Darcy），另一个是内部损失项：

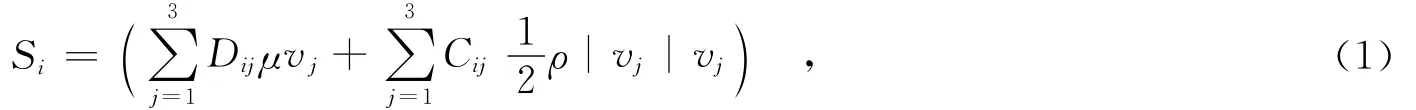
其中，Si是i向（x，y或z）动量源项，vj是j向（x，y或z）的瞬时速度，ρ为流体密度，μ是流体粘度，D和C是规定的矩阵.在多孔介质单元中，动量损失对于压力梯度有贡献，压降和流体速度（或速度方阵）成比例.对于简单的均匀多孔介质，简单的指定D和C分别为对角阵1／α和C2，其他项为0，得

式中，α是渗透阻力系数，即渗透率，若已知水力传导系数K，而K＝αρg／μ，可求得α＝Kμ／（ρg）.C2是内部阻力因子，即惯性阻力系数，在地下水低流速下定义水流状态为层流，通过多孔介质的层流流动中，压降和速度成比例，惯性阻力系数C2设为0.

2 实验室构建简化可渗透反应墙及试验结果

采用柱体实验，实验装置图如图1所示.柱体直径为16 cm，充填平均粒径5 mm的陶粒，有效高度Δh＝86 cm，L＝66 cm.运用排水法实验数据及计算如表1、表2所示，计算得出小球构成的柱体总孔隙度V加水饱和／V干试样＝0.44，给水度Sy＝V排水／V加水＝0.305.由于给水度与总孔隙度计算的值有差异，说明陶粒小球有不连通的孔隙，而有效孔隙度值n应在总孔隙度和给水度之间，这里取n＝给水度值Sy，即n＝0.305.又由于该可渗透反应墙设计水力停留时间为24 h，水力传导系数K＝V·L／（Δh·A·t），实验数据如表3所示，计算得出K平均值为1.117 mm／s，进而计算得出陶粒床层渗透阻力系数α＝1.14×10-10m2.

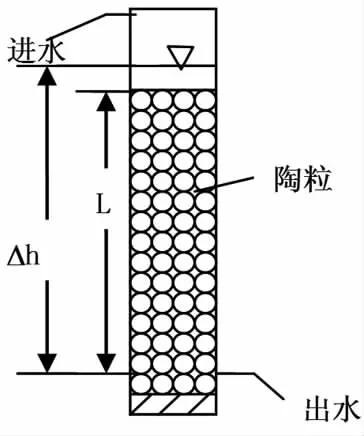
图1 实验装置简化图

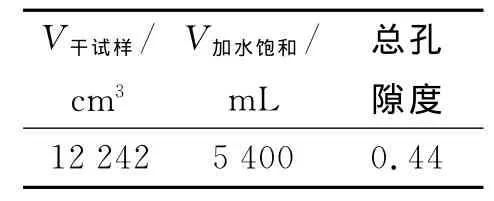
表1 柱体总孔隙度

表2 给水度

表3 水力传导系数K和渗透阻力系数

3 Fluent软件构建可渗透反应墙及模拟计算与分析

3.1 Fluent软件构建可渗透反应墙

虽然根据前期基础实验数据分析得出了部分参数，但是试验发现柱体壁流现象比较明显，不能真实地反应PRB内部的流态情况.我们又重新设计组装实验室模拟试验的矩形PRB槽，槽体尺寸为120×30×25 cm，进出水均采用蠕动泵，槽体中间装填有长度为100 cm的陶粒介质段.

将实验装置简化为二维图（见图2）来观察PRB内流态模拟状况.边界条件：速度进口（velocity-inlet），出口为outflow类型，内部单元区域采用流体（fluid）类型，其余四周采用壁面（wall）类型.基本参数（部分参数取自上述实验结果）如下：v＝1 mm／s，1／α＝8.77×109m-2，C2＝0，μ＝10-3Pa·s，ρ＝10-3kg／m3，n＝0.305.

求解设置：选用基于压力的二维定常解算器，残差在迭代100次后小于10-4，认为计算收敛[5-6，8].

从Fluent模拟实验室自组装可渗透反应墙墙体内流场可以看出：①水流在流入多孔介质时受到介质阻力（见图3），流速降低至入水口流速的6.67%；②在该实验装置下，流体流经介质时低流速下基本保持层流状态，中间流量较大，边界存在壁流粘滞阻力影响，流速较慢，流量较小（见图4，注：流函数是单位时间流体通过介质的流量），反应墙介质内中间流量与边界流量相差约6倍；③流体在未流入介质之前由于介质阻力产生了一定涡流现象（见图5，注：中间线为对称轴）.

模拟后发现基于Fluent自定义多孔介质只能进行动量转化，不能对多孔介质材料内部流态进行可视化模拟与水流速度数值计算，必须采用三维模拟方式.

3.2 三维情况下模拟水流区域

鉴于在二维构建平面陶粒时，陶粒与陶粒间不能紧密相连，水流速度在该区域模拟运算不符合实际三维流动情况，故改用在三维视角下模拟水流区域.

首先运用GAMBIT网格化定义三维试验区域（见图6），将水流区域简化为为30×20×20 mm的矩体，矩体内小球直径为5 mm，从左至右第1层有4×4个小球，第2层3×3个小球，第3层4×4个小球（将若干堆积陶粒堆积的墙体简化为3层小球，3层小球基本上可以反映出多层小球累积的多孔介质）.

图2 简化二维图

图3 速度等值线图

图4 流函数图

所研究液体为水，为粘性、不可压、牛顿流体，流动方向从左至右，垂直于Y-Z面（沿X方向），层流，定常流动.设定水流面初始速度为1 mm／s，流出面为自由流出.基本参数取值同上二维模型.

初始化后，由软件模拟迭代200次，残差得到很好收敛，得到以下结果：（剖面总图见图7，左面为入口面，右面为出口面，中间球状物为介质陶粒，切面为剖面在水流区域位置）

图5 速度矢量图

图6 三维水流区域

图7 剖面总图

①横断水流方向上过陶粒球心的面如图8所示.由图8可以看出，陶粒外部速度很快，越接近表面其速度越慢；剖面X＝12.5速度分布变化趋势如图9所示.由图9可以看出，在该剖面上球体内水流速度可以衰减到接近为0，球体外流速最高值可以比入口流速快3.47倍，而该剖面上平均流速则只有入口流速的75.2%，说明陶粒介质对流速存在阻力衰减，而壁面流速下降很快，则表明液体的粘滞阻力在低流速下对实验室装置条件下的污染物溶质运移会有一定影响；水流穿过介质后在该矩体内的速度等值线图如图10所示；剖面X＝25速度分布变化趋势如图11所示.图11符合低流速下层流的状态，该剖面上平均速度与图8剖面的平均速度值基本相等，说明填充介质陶粒对整个流体的宏观流速影响不大，而陶粒间流速由于在水头压力作用下会变大.

图8 剖面X＝12.5速度等值线图

图9 剖面X＝12.5速度分布变化趋势图

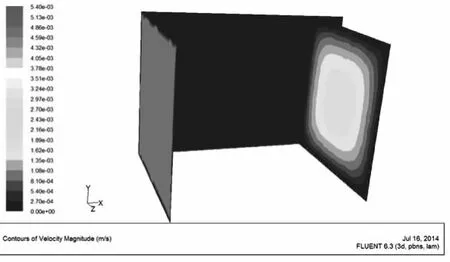
图10 剖面X＝25速度等值线图

②水流方向上穿过陶粒球心的面如图12所示.由图12可以看出，陶粒由外部向内部速度明显呈递减趋势，穿过陶粒介质之后，水流稳定为层流状态，水流速度从中间向两壁逐渐递减，靠近壁面时流速下降很快；剖面Z＝12.5速度矢量图如图13所示.由图13可以看出，在流经陶粒区域低流速下，雷诺数较小，未产生涡流现象.该剖面上最大流速比入口流速要高82.1%，沿X方向平均流速为入口流速的67.5%.

③水流方向上不穿过陶粒球心剖面Z＝15的面如图14所示.由图14可以看出，陶粒间流速相对较快，缝隙越小流速越快（由于三角网格面积还是过大导致该剖面速度变化曲线不能够圆滑）；剖面Z＝15速度变化趋势图如图15所示.由图15可知，其流速最高能达到进水流速的5.2倍，与剖面Z＝12.5相比的1.821倍，流速此剖面上要更快.这是因为入水面和出水面之间没有陶粒介质阻挡，因此在构建可渗透反应墙时，需要考虑墙体的结构设计类型[9]，应完全堵住污染物羽状分布区域，否则会使得局部流速过快，避开了可渗透反应墙，而使得局部污染严重，达不到治理污染的效果.

④水平切面方向上只穿过第2层陶粒球心的剖面如图16所示，穿过第1层和第3层陶粒球心的剖面如图17所示.由图16、图17同样可以得出上面的结论，在低流速（地下水流速）下水流穿过可渗透反应墙介质时孔隙流速相对较快，而陶粒内部流速相对很慢，将生物菌固定在陶粒内部生长是可行的，同期试验结果也表明在固定了硫酸盐还原菌的同时改变进水流速的情况下，酸性矿井水中硫酸根浓度还是有一定的降解速率[4，10]，同时也可以得到若在可渗透反应墙墙体内固定生物菌后，其固定相吸附解吸一阶反应速率与溶解相一阶反应速率[10]与流过水流的流速呈一定的相关性.

图11 剖面X＝25速度分布变化趋势图

图12 剖面Z＝12.5速度等值线图

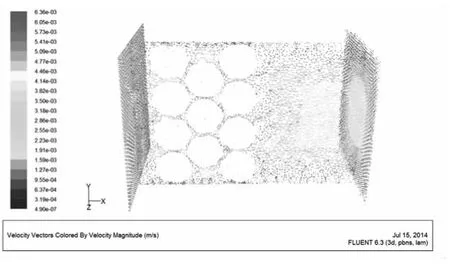
图13 剖面Z＝12.5速度矢量图

图14 剖面Z＝15速度等值线图

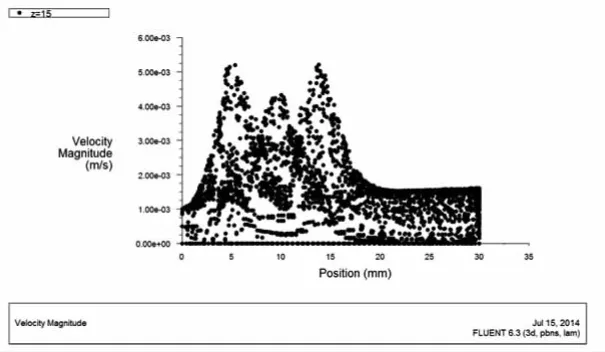
图15 剖面Z＝15速度变化趋势图

图16 剖面Y＝10速度等值线图

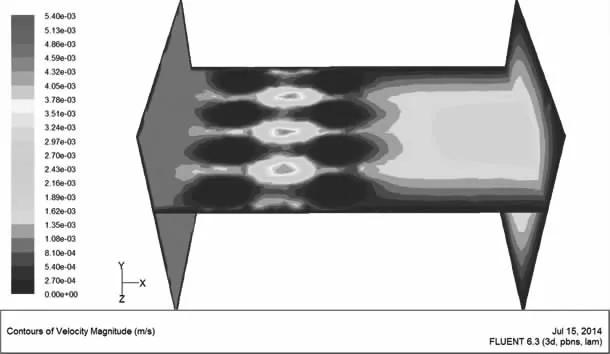
图17 剖面Y＝10速度等值线图

4 结论

模拟仿真结果表明：低流速下（如地下水流速），可渗透反应墙墙体内平均流速受到流体的粘滞阻力的影响，与流体本身的性质相关.而填充介质陶粒内部流速相当缓慢，速度下降很快，可以很好地固定生处理污染物质的生物菌，陶粒间缝隙速度一般为进水流速的3～4倍，甚至更高，这为可渗透反应墙的设计提供一些参考.利用CFD软件Fluent可以微观模拟仿真可渗透反应墙墙体水流状态，从而推导其溶质运移情况.在实验基础上得到可渗透反应墙相关影响因子的溶质运移衰减的动力学方程，通过编写UDF加载到Fluent软件中，

从而可以更真实地反映可渗透反应墙处理废水的情况.

[1]何玲芳.酸性矿坑废水原位治理技术[J].节能与环保，2008，3：27-29.

[2]丛致远，赵峰华，郑晓燕.煤矿酸性矿井水研究进展[J].煤炭环境保护，2002，16（5）：8-12.

[3]熊玲，张瑞雪，吴攀，等.碳酸盐岩处理煤矿酸性废水的试验研究[J].水处理技术，2010，36（8）：45-48.

[4]罗亚楠.可渗透反应床固定化硫酸盐还原菌原位治理酸性矿井水技术的研究[D].芜湖：安徽工程大学，2013.

[5]王福军.计算流体动力学分析[M].北京：清华大学出版社，2004.

[6]韩占忠.FLUENT——流体工程仿真计算实例与分析[M].北京：北京理工大学出版社，2009.

[7]孔德川，丁爱中，郑蕾，等.分层式潜流人工湿地水力学特性数值模拟与分析[J].环境工程学报，2011，5（4）：741-744.

[8]王瑞金，张凯，王刚.Fluent技术基础与应用实例[M].北京：清华大学出版社，2007.

[9]楼静，马兴冠，景长勇，等.PRB在酸性矿井水处理中的应用分析[J].矿业安全与环保，2008，35（3）：83-85.

[10]王岩.酸性矿井水对地下水污染规律的数值模拟研究[D].沈阳：辽宁工程技术大学，2007.