泡沫金属的微惯性效应和动态塑性泊松比＊

王长峰，郑志军，虞吉林

（中国科学技术大学中国科学院材料力学行为与设计重点实验室，安徽 合肥230026）

泡沫金属具有稳定且可持续吸收能量的平台应力，作为吸能材料在工业领域应用广泛。在实际应用中，泡沫金属大多经受复杂加载状态，因而了解泡沫金属在多轴加载下的力学行为有重要的意义。

准静态条件下，许多学者给出了泡沫金属多轴加载下的唯象屈服表面。G.Gioux等［1］给出了开孔和闭孔泡沫金属准静态条件下唯象的屈服表面，M.Doyoyo等［2］给出了以拉伸加载状态为主的唯象屈服表面。V.S.Deshpande等［3］给出了唯象的屈服表面及其演化规律。C.Chen等［4］在理论上提出了一个泡沫金属本构模型的唯象框架，能够很好地描述泡沫金属在压缩主导的应力状态下的响应。泊松比作为材料本构模型中的重要参数，影响着屈服面的形状，因而得到泡沫金属泊松比的准确结果有着重要的意义。由于泡沫金属的不规则性，在实验中很难准确测量泡沫金属的泊松比。G.Gioux等［1］测量了相对密度7%的Duocel泡沫和相对密度8%的Alporas泡沫，认为其塑性泊松比分别为0.052和0.024。V.S.Deshpande等［3］测量了相对密度16%的Alporas泡沫和相对密度7%的Duocel泡沫，认为其塑性泊松比分别约为0.2和0.15。即便是相同相对密度的Duocel泡沫，其塑性泊松比的测量结果也存在较大的差异。在动态冲击条件下，J.L.Yu等［5］发现闭孔泡沫金属在侧向约束条件下动态压溃应力随着加载速率的增加有显著下降。为了解释这个现象，要对泡沫金属动态塑性泊松比问题有较深入的研究。但由于实验条件和测量手段的限制，测量泡沫金属动态塑性泊松比是非常困难的，P.S.Kumar等［6］和S.L.Lopatnikov等［7］认为泡沫金属的动态塑性泊松比为0，但是没有给出具体的测量结果。数值模拟方法能够克服实验测量手段的限制，采用泡沫金属的细观有限元模型，可以定性研究泡沫金属塑性泊松比的变化规律。

本文中采用三维Voronoi结构的开孔和闭孔泡沫金属模型，研究2类泡沫金属动静态加载条件下塑性泊松比的变化规律，并讨论相对密度和冲击速度对其的影响，进而分析微惯性对泡沫金属轴向冲击性能的影响，并对实验中的现象给出了解释。

1 数值模拟

1.1 三维Voronoi构型

为了得到与真实泡沫相似的几何构型，采用三维随机Voronoi技术［8］构建了闭孔和开孔2种泡沫金属的细观模型。在给定的体积为V0的区域上随机撒下N个点，如图1（a）所示，满足任意两点的距离δ不小于一定的给定的距离δmin，其定义为：

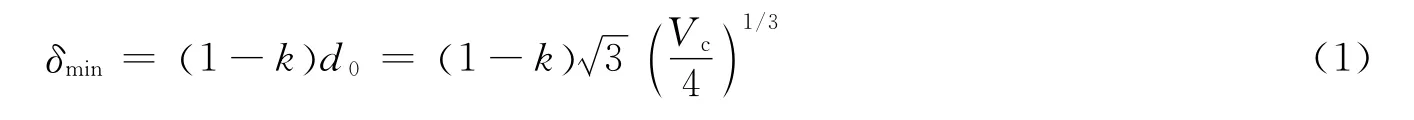
式中：k为不规则度，d0和Vc分别为规则正十四面体模型中最邻近成核点之间的距离和单胞的体积。

这N个成核点被拷贝到周围的26个区域中，通过这27 N个成核点生成Voronoi构型，最后通过切割算法获取原先指定空间区域内的Voronoi结构。采用Voronoi构型的胞元表面结构来构建闭孔泡沫金属的细观有限元模型，采用胞元棱边来构建开孔泡沫金属的细观模型，分别如图1（b）和（c）所示。

图1 含600个胞元的三维Voronoi构型Fig.1 Three－dimension voronoi models with 600nucleus

1.2 有限元模型

有限元模型的几何尺寸为20mm×20mm×30mm，长轴为加载方向。整个几何模型含有600个胞元，不规则度为0.5。并假定基体为弹性－理想塑性材料，密度ρs＝2.77g／cm3，杨氏模量Es＝69GPa，弹性泊松比νs＝0.3，屈服强度σys＝170MPa。泡沫模型上下表面添加刚性表面，下部的刚性表面固定，上部的刚性面以恒定的冲击速度v压缩泡沫样品。泡沫模型和刚性平面，以及泡沫模型内部的结构施加了接触。为了着重探讨细观拓扑结构、相对密度和冲击速度对泡沫金属宏观力学行为的影响，近似忽略摩擦的影响，在计算模拟过程中将摩擦系数设为0.02［9］。

对于闭孔泡沫金属模型，假定泡沫金属有均匀的厚度，其相对密度可以表示为：

式中：ρ0是泡沫材料的密度，ρs是基体材料的密度，V是泡沫材料的体积，Ai是第i个胞壁的表面积，h为泡沫材料的胞壁厚度。模型的有限元单元采用ABAQUS中的S3R和S4R壳单元。通过网格敏感性分析，壳单元的特征长度设置为0.3mm，最终划分为约170 000个壳单元，其中包括约20 000个S3R单元和150 000个S4R单元。

对于开孔泡沫金属模型，假定所有棱边有相同的横截面面积A，其相对密度可以表示为：

式中：Li是第i个棱边的长度。采用ABAQUS中的B31单元模拟。通过网格敏感性分析，梁单元的特征长度为0.25mm，最终划分成约38 000个梁单元。

2 计算结果与分析

2.1 变形模式

相对密度为0.1的开孔和闭孔泡沫金属在不同冲击速度下的变形分别如图2（a）、（b）所示。无论是开孔泡沫金属还是闭孔泡沫金属，在不同冲击速度下的变形都可以分成3种主要的模式。这与二维随机蜂窝观察到的变形模式是一致的［9－10］。在冲击速度较低时（如1m／s），其变形较为均匀，表现为随机分布的剪切变形带，称之为“均匀模式”。当冲击速度很高时（如110m／s），泡沫金属表现为逐层压溃变形，在冲击端附近形成很窄的变形带，称为“冲击模式”。当冲击速度介于这两者之间时，泡沫金属的变形带比较集中于冲击端，形成较为局部的变形带，称为“过渡模式”。

图2 泡沫金属在不同冲击速度下的变形模式Fig.2 Deformation modes of metallic foam under different impact velocities

2.2 临界速度

为了描述随机蜂窝材料的变形／应力均匀性，Y.D.Liu等［10］引入了应力均匀性指标：

式中：σ（s）pl和σ（i）pl分别为支撑端和冲击端的平台应力。同时认为均匀性指标90%可作为一个临界值，对应于从均匀模式到过渡模式的临界转变速度。相对密度为0.1的闭孔和开孔泡沫金属的均匀性参数φ随冲击速度的变化规律分别如图3（a）、（b）所示。

图3 泡沫金属的应力均匀性指标随冲击速度变化关系Fig.3 Stress uniformity index varied with impact velocity for metallic foam

对于闭孔泡沫金属，临界转变速度为56.7m／s，对于开孔泡沫金属，临界转变速度为39.7m／s。当冲击速度很高时，泡沫金属模型的变形处于过渡模式或冲击模式，局部变形会使得泡沫金属的力学行为更多地表现为一种结构响应，而非材料响应。这时试件横向变形的宏观度量失去意义，定义的动态塑性泊松比偏差较大。因而泡沫金属动态泊松比问题仅仅限定在泡沫金属处于“均匀模式”下讨论。

2.3 相对密度对塑性泊松比的影响

泡沫金属塑性泊松比定义为横向塑性应变（εx和εy的平均值）的负值与轴向塑性应变εz的比值：

在低速冲击（1m／s）下，不同相对密度的闭孔和开孔泡沫金属的名义塑性泊松比随着轴向应变的变化分别如图4（a）、（b）所示。计算结果表明，当轴向应变较小时，名义塑性泊松比的值较大，随着相对密度的增大，2种泡沫金属的塑性泊松比和初始的峰值均有明显的提高。

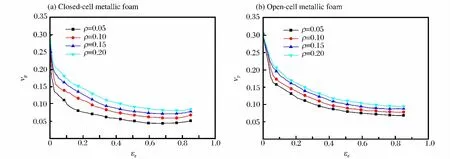
图4 不同相对密度的泡沫金属的塑性泊松比随轴向应变的变化Fig.4 Plastic Poisson’s ratio varied with longitudinal strain for foams with different relative densities

2.4 冲击速度对塑性泊松比的影响

在不同的冲击速度下，相对密度为0.1的闭孔和开孔泡沫金属的塑性泊松比随轴向应变的变化如图5所示。图6所示为塑性泊松比峰值随冲击速度的变化，随着冲击速度提高，闭孔和开孔泡沫金属的塑性泊松比的峰值有明显下降。

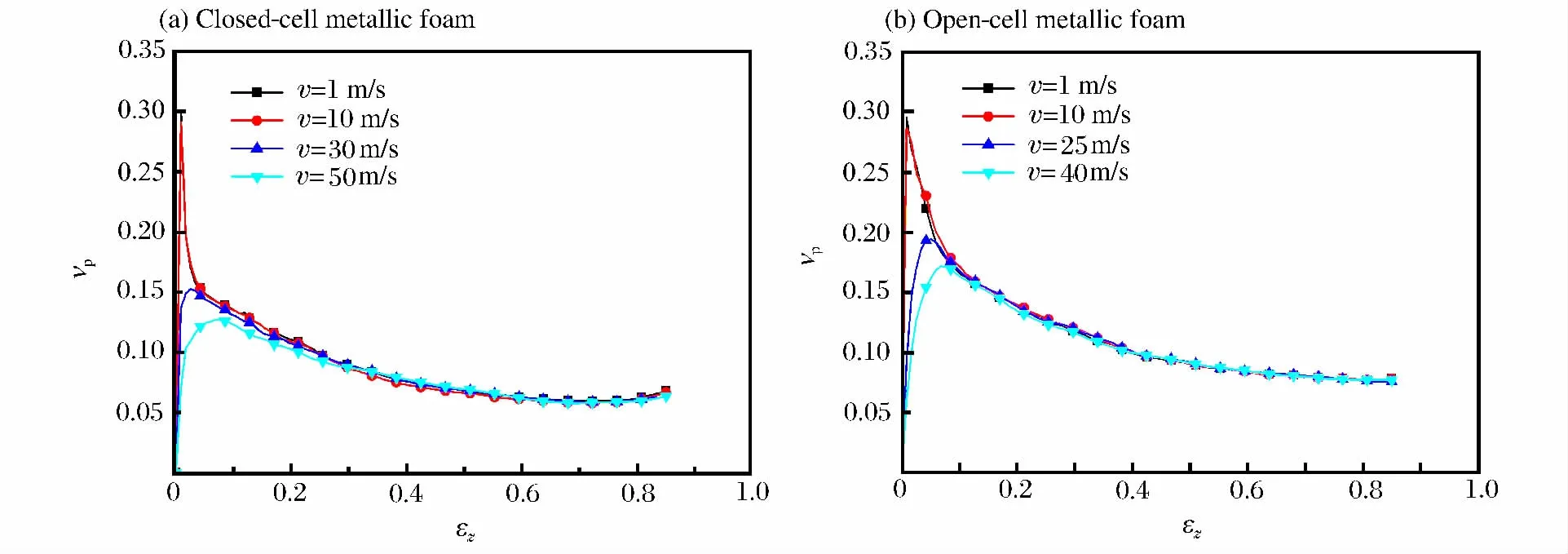
图5 不同冲击速度下泡沫金属塑性泊松比随轴向应变的变化Fig.5 Plastic Poisson’s ratio varied with longitudinal strain at different impact velocities

塑性泊松比随着冲击速度的下降可以解释为：在准静态单轴压缩情况下，由于泊松效应，泡沫会发生横向膨胀。当冲击速度很低时，泡沫有充分的时间发生横向变形；但当冲击速度提高时，由于横向惯性的存在，泡沫金属来不及发生横向变形。因而，塑性泊松比随着冲击速度的增加，其峰值下降。

以上机制可以解释文献［5］中的实验现象。当施加侧向约束后，在准静态加载下，较高的塑性泊松比初始峰值导致较大的变形阻力，泡沫金属的初始压溃应力提高。当冲击速度较高时，塑性泊松比的初始峰值很低，侧向阻力减弱，所以侧向约束条件下泡沫金属的压溃载荷随着加载速率的提高而降低。

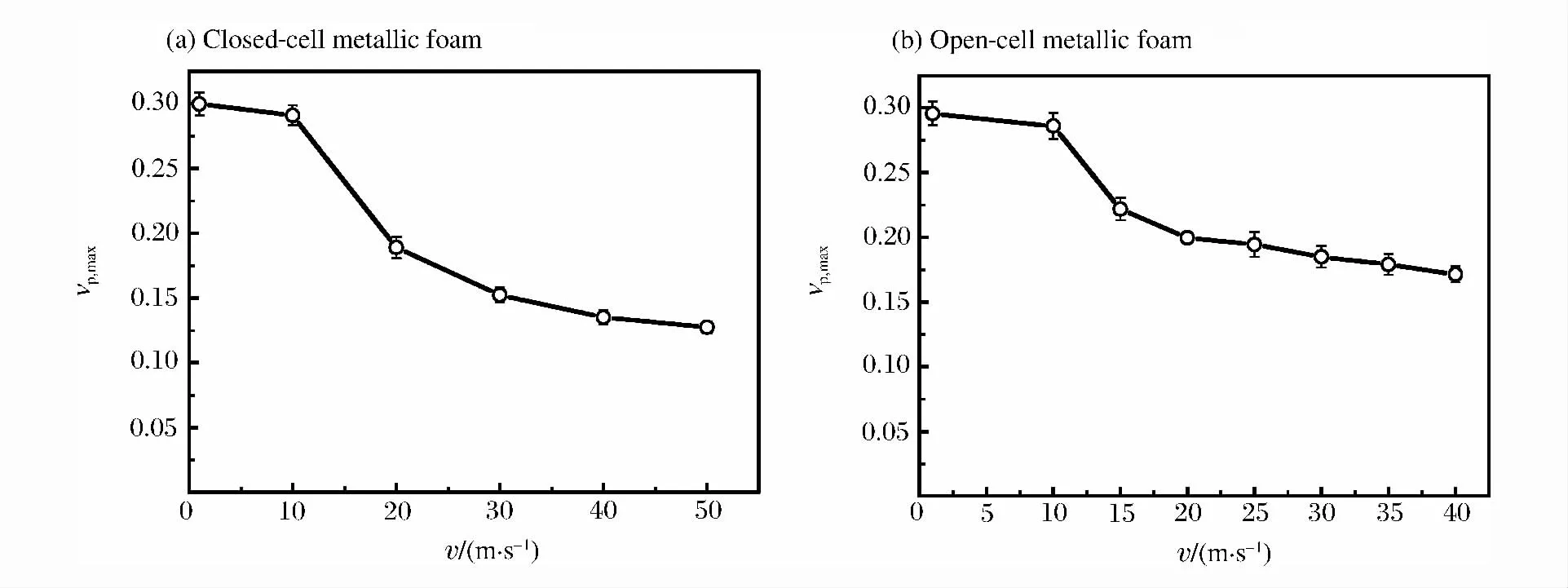
图6 泡沫金属塑性泊松比峰值随冲击速度的变化Fig.6 Peak value of plastic Poisson’s ratio varied with impact velocity

2.5 微惯性效应

横向惯性的存在会直接影响泡沫金属的动态塑性泊松比。由于泡沫金属材料中存在大量空隙，局部的横向变形并不会对周围材料产生影响，这种横向惯性效应实际上是一种微惯性。对于微惯性效应的存在是否影响泡沫金属的轴向力学性能，文献中有一些冲突的观点。一些研究者认为，细观结构的微惯性对金属泡沫的动态增强效应起到了非常重要的作用［11－13］；但另外一些研究者认为，微惯性对泡沫金属的动态增强效应的影响很微弱［14］。为了量化微惯性效应，即横向惯性对轴向力学性能的影响，Y.D.Liu等［10］引入了微惯性参数μ，定义为泡沫金属所有节点的侧向加速度平方根（Ax和Ay）和纵向加速度平方根（Az）之比：

对于不同冲击速度下的微惯性参数随轴向应变的变化，如图7所示。

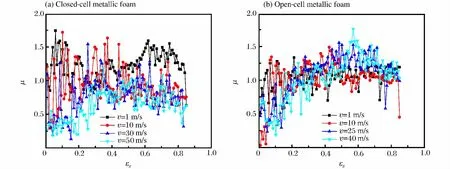
图7 泡沫金属微惯性参数随轴向应变的变化Fig.7 Micro－inertia parameter varied with longitudinal strain for metallic foam

图8所示为泡沫金属的微惯性参数的平均值与冲击速度的关系，从图8（a）中可知闭孔泡沫金属的微惯性参数的平均值随着冲击速度的下降而下降；从图8（b）中可知，开孔泡沫金属的微惯性参数的平均值随着冲击速度的增加基本保持恒定。并且它们的数值与密实固体材料同量级，远小于典型的第二类结构的微惯性参数［10］。这说明三维泡沫金属不是典型的第二类结构，微惯性效应是微弱的。

图8 泡沫金属微惯性参数随冲击速度的变化Fig.8 Micro－inertia parameter varied with impact velocity

3 结 论

采用三维细观有限元模型模拟了闭孔和开孔2种泡沫金属的动态压缩响应。结果显示2种三维泡沫金属均与二维随机蜂窝有类似的变形模式分类，即随着冲击速度的提高出现均匀模式、过渡模式和冲击模式。当发生均匀模式的变形时，开孔和闭孔泡沫金属的塑性泊松比均不是一个常数，塑性泊松比随着轴向应变的增加而下降。当相对密度增加时，泡沫内部孔隙减少，导致泡沫金属的塑性泊松比有明显的提高。而随着冲击速度的增加，泡沫金属的动态塑性泊松比随着轴向应变的增加有明显的下降。这是由于横向惯性的存在，随着速度提高，泡沫金属中以细观结构崩塌为主导的变形来不及引起宏观的侧向膨胀，从而解释了文献［5］中实验观察到的现象。通过分析横向惯性对平台应力的影响，发现对于闭孔和开孔泡沫金属，微惯性效应相比典型的第二类结构来说要小的多。因此，泡沫金属不是典型的第二类结构，微惯性对平台应力的影响是非常微弱的。

［1］Gioux G，McCormack T M，Gibson L J.Failure of aluminum foams under multiaxial loads［J］.International Journal of Mechanical Sciences，2000，42（6）：1097－1117.

［2］Doyoyo M，Wierzbicki T.Experimental studies on the yield behavior of ductile and brittle aluminum foams［J］.International Journal of Plasticity，2003，19（8）：1195－1214.

［3］Deshpande V S，Fleck N A.Isotropic constitutive models for metallic foams［J］.Journal of the Mechanics and Physics of Solids，2000，48（6／7）：1253－1283.

［4］Chen C，Lu T J.A phenomenological framework of constitutive modelling for incompressible and compressible elasto－plastic solids［J］.International Journal of Solids and Structures，2000，37（52）：7769－7786.

［5］Yu J L，Wang E H，Li J R.An experimental study on the quasi－static and dynamic behavior of aluminum foams under multi－axial compression［M］.Lancaster：D E Stech Publications，2008：879－882.

［6］Kumar P S，Ramachandra S，Ramamurty U.Effect of displacement－rate on the indentation behavior of an aluminum foam［J］.Materials Science and Engineering：A，2003，347（1／2）：330－337.

［7］Lopatnikov S L，Gama B A，Haque M J et al.Dynamics of metal foam deformation during Taylor cylinder－Hopkinson bar impact experiment［J］.Composite Structures，2003，61（1／2）：61－71.

［8］Okabe A，Boots B，Sugihara K.Spatial tessellations：Concepts and applications of Voronoi diagrams［M］.Chichester Wiley，1992：229－287.

［9］Zheng Z J，Yu J L，Li J R.Dynamic crushing of 2Dcellular structures：A finite element study［J］.International Journal of Impact Engineering，2005，32（1／2／3／4）：650－664.

［10］Liu Y D，Yu J L，Zheng Z J，et al.A numerical study on the rate sensitivity of cellular metals［J］.International Journal of Solids and Structures，2009，46（22／23）：3988－3998.

［11］Raj R E，Parameswaran V，Daniel B S S.Comparison of quasi－static and dynamic compression behavior of closedcell aluminum foam［J］.Materials Science and Engineering：A，2009，526（1／2）：11－15.

［12］Vesenjak M，Veyhl C，Fiedler T.Analysis of anisotropy and strain rate sensitivity of open－cell metal foam［J］.Materials Science and Engineering：A，2012，541：105－109.

［13］Montanini R.Measurement of strain rate sensitivity of aluminium foams for energy dissipation［J］.International Journal of Mechanical Sciences，2005，47（1）：26－42.

［14］Deshpande V S，Fleck N A.High strain rate compressive behaviour of aluminium alloy foams［J］.International Journal of Impact Engineering，2000，24（3）：277－298.