基于遗传算法的海杂波K分布参数估计
2014-12-07朱人杰陈红卫
朱人杰,陈红卫
(江苏科技大学 电子信息学院,江苏 镇江212003)
0 引 言
大量实例表明,当雷达分辨力较低或在大的观测角下,海杂波的幅度分布可用瑞利分布表示,但在高分辨率雷达低擦地角情况下,海杂波的幅度分布不再服从瑞利分布,此时可用对数正态分布、韦布尔分布等来拟合。但对窄脉冲雷达的测量与分析发现,海杂波幅度会出现很长的拖尾情况,Jakeman和Pusey 第一次将K分布模型[1]用于海杂波模型研究。
针对海杂波K分布模型,为能得到精确的统计模型,关键在于对模型参数进行最优估计。目前常用的有效估计方法包括最大似然法、矩估计法[2]、神经网络估计法等。其中最大似然法的精度最高,但其模型解析式较难获得。而神经网络法估计结果虽精确,但收敛时间较长,需要多次迭代,不适用于实时计算。因此在工程上大都采用运算相对简单,适用性较广的矩估计法,它计算简单且能达到一定的精度。V.Anastassopou los 等提出的高阶矩估计法估计参数仅是在矩估计的基础上,对多参数进行优化,并没有从根本上解决全局搜索的非线性问题[3]。本文从不依赖于非线性模型表达式的参数估计出发,寻求一种解决海杂波模型参数估计的方法。
遗传算法(GA)是模拟遗传选择和生物进化过程的计算模型,是基于自然选择和基因遗传学原理的有导向随机搜索算法。同时它具有全局搜索能力强、计算简单、鲁棒性强、并行处理及高效实用等显著特点。本文在两参数的K分布参数估计过程中,建立非线性最优化模型,利用GA 对杂波幅度模型的参数进行优化计算,并用Matlab 实现所提出的方法。
1 复合K分布模型
复合K分布模型是基于广义Gamma分布模型提出的复合分布模型的一种应用[4]。K分布的概率密度函数如式(1)所示。在此模型中,海杂波回波的幅度被描述为2个因子的乘积:第1 部分是斑点分量(即快变化分量),它由大量散射体的反射进行相参叠加而成,符合瑞利分布;第2 部分是基本幅度调制分量(即慢变化分量),它反映了与海面大面积结构有关的散射束在空间变化的平均电平,具有长相关时间,服从Gamma分布。
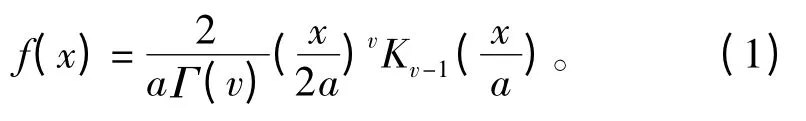
式中:Γ(·)为Gamma 函数;Kv-1(·)为v-1 阶第二类修正Bessel 函数;a为尺度参数;v为形状参数。
对于大多数海杂波,形状参数的取值范围为0.1 <v <∞,当v →∞时,杂波的分布接近于瑞利分布。而对于高分辨率低擦地角的海杂波v的值在0.1~3 之间。图1和图2 给出了K分布概率密度随尺度参数a 及形状参数v的变化情况。
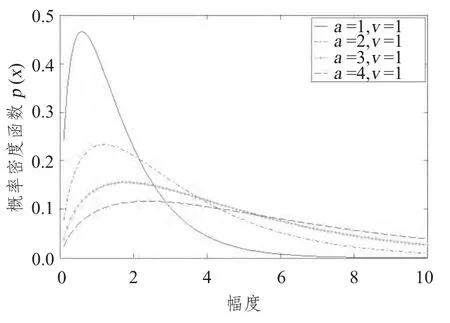
图1 K分布概率密度随尺度参数a 变化Fig.1 The pdf of K distribution with a
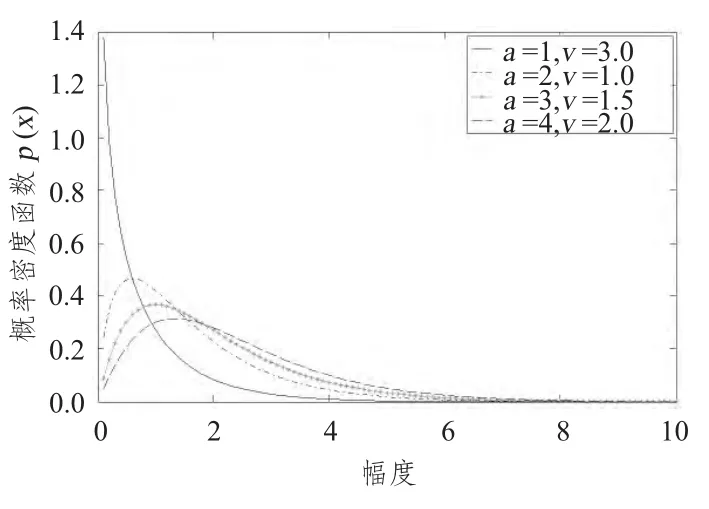
图2 K分布概率密度随形状参数v 变化Fig.2 The pdf of K distribution with v
2 遗传算法及其改进
2.1 遗传算法基本原理
遗传算法(GA)是一种以自然选择和遗传理论为基础,将生物进化过程中适者生存规则与群体内部染色体的随机信息交换机理相结合的搜索算法[5]。遗传算法把问题的解表示成染色体,在算法中是以二进制编码串表示,并在执行遗传算法之前,给出一群染色体,即是假设解。然后把这些假设解置于问题的环境中,并按适者生存的原则,从中选择出较适应环境的染色体进行选择,再通过交叉、变异的过程产生更适应环境的新一代染色体群。通过不断的进化,最后收敛得到最适应环境的染色体,即问题的最优解。
2.2 遗传算法的改进
为改善遗传算法的实际性能[6],将从编码方案、适应度函数标定等方面进行算法改进。
编码是遗传算法应用需要解决的首要问题,也是设计遗传算法的一个关键步骤。编码的好坏直接影响算法中选择、交叉、变异等遗传运算。传统的编码采用二进制0,1 字符构成的固定长度串,它的缺点之一是具有较大的汉明(Hamming)距离,因为在某些相邻整数的二进制代码之间有很大的差别,比如用4 位二进制编码7和8 时,分别为0111和1000,此时若要实现从7 到8的改变,必须改变所有编码位,这种缺陷使得遗传算法的交叉和变异难以跨越,降低了遗传算法的搜索效率。
为此本文采用格雷码(Gray Code),使得相邻整数之间汉明距离都为1,能有效避免这一缺陷。格雷码的特点是任意2个连续的整数所对应的编码之间仅有1 位编码不同,其余均相同。把二进制码b1b2…bn转换成对应的格雷码a1a2…an,采用式(2)完成变换任务。

经仿真表明,遗传算法采用格雷码具有提高遗传算法的局部搜索能力、利于实现交叉、变异等遗传操作、符合最小字符集编码原则以及便于利用模式定理对算法进行理论分析等优点。
同样,适应度函数的标定也是整个算法的关键。适应度函数是根据目标函数确定的用于区分群体中个体好坏的标准,是进行自然选择的唯一依据。因此在函数的设计上必须满足计算量小、通用性强等原则。为此本文中选择实测数据密度函数曲线与理论模型概率密度函数之间距离的倒数为适应度函数。此外,为避免收敛过早和除法运算出错,在分母上进行加1 处理,如下式所示:

2.3 多种群遗传算法
标准遗传算法的全局搜索能力较强,局部搜索能力较弱,出现未成熟收敛[7],主要体现在种群中的个体均趋于统一状态而停止进化,从而得不到最优解。多种群遗传算法可以较好地解决这个问题,其算法结构如图3所示。它引入多个群体同时优化。对于不同种群采用不同的控制参数,并通过移民算子进行连接,实现了多种群的协同优化。
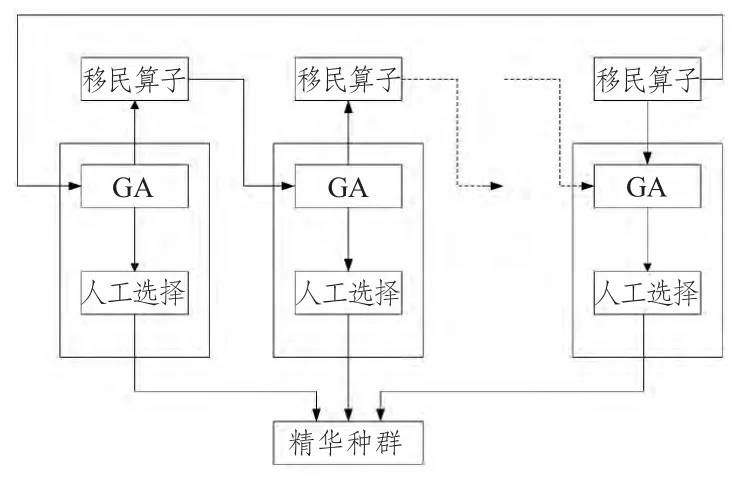
图3 多种群遗传算法结构示意图Fig.3 Poly-population Genetic Algorithm structure
移民算子在多种群算法设计中至关重要,它将各个群中进化的最优个体定期地引入到其他种群中,实现种群间的相互联系。具体操作是将目标种群中最差个体用源种群的最优个体替代,在进化的每一代结果中,通过人工选择选出各个种群最优个体,放入精华种群并保存。为了保证进化过程中产生的最优个体不被破坏和丢失,精华种群并不参与选择、交叉、变异操作。
3 基于遗传算法的参数估计
将遗传算法应用于海杂波K分布模型的尺度参数a、形状参数v 估计中,其流程如图4所示。步骤如下:
1)设定终止条件、交叉概率和变异概率。
2)编码:将a1,v1,…ak,vk按各自需要的精度用二进制串表示,然后将其连接成一个单一的L 格雷码串。
3)产生初始种群:随机产生n个L 位的二进制串。
4)确定适应函数:参数搜索范围可以选择参数的经验区间[8],针对高分辨率低擦地角的海杂波的情况,参数搜索范围选用经验区间[0,5]。适应度函数的选择是遗传算法用于参数估计的重点,好的适应度函数可以减少计算量以及计算时间,确保得到全局最优的搜索结果,并计算初始种群每个染色体的适应度值和适应度概率。
5)产生子代个体:根据适应度概率从种群中选择S个染色体进行交叉和变异,产生子代个体。
6)选择:将适应度概率最大的个体作为当前最优个体,并保留;直接选取交换后的群体中具有最大适应度的前N个个体作为下一代进行繁殖。这一步骤的存在使得当前群体是所有搜索过的解中最优的前N个的集合。
7)交叉:以概率fi/∑fi从种群中选出n个串(父串),以概率pc(交叉概率)在一随机位置进行交换,按它们的适应值从大到小排序,取前面一半为新一代解群。
8)变异:在新的种群中挑出1个个体,在一随机位置进行变异。在群体中随机选择一定数量个体,对于选中的个体以概率pm(变异概率)随机地改变串结构数据中某个基因的值。计算子代个体的适应度值和适应度概率,人工选出各个种群最优个体,放入精华种群并保存。
9)判断最优个体保持代数是否满足要求,若满足结束算法,否则转步骤5 继续。

图4 遗传算法参数估计流程Fig.4 Parameter estimation of Genetic Algorithm
4 仿真与分析
4.1 仿真实验及结果
实验中海杂波实测数据来自CSIR (The Council for Scientific and Industrial Research)组织的网站http://www.csir.co.za/small _ boat _ detection/mtrials02.html,提供的数据已被归一化成标准的数据。实验中编码长度取L =20,初始种群N =40,以最优个体保持代数作为结束标志,图5 是海杂波数据用改进遗传算法对K分布模型参数进行估计的适应度值的变化情况,从中可以看出标准遗传算法在起始的1~20 代中,适应度值快速收敛,而在其后的20~50 代中两者变化缓慢直至平稳。而采用多种群遗传算法的稳定性更好,收敛速度更快,使用的遗传代数更少,适合复杂问题的优化。

图5 遗传算法进化过程图Fig.5 Genetic Algorithm evolutionary process
为体现改进遗传算法用于海杂波K分布模型参数估计的有效性及适应非线性系统模型的优点,实验将原始海杂波数据与改进遗传算法拟合曲线进行对比研究,结果如图6所示。

图6 实测杂波与优化曲线Fig.6 The measured clutter and optimized curve
4.2 均方差检验
为了进一步得到定量分析结果,采用均方差(Mean Squared Deviation,MSD)进行检验。均方差检验法是统计学中常用的检验方法,其如下式所示:

式中:pe,pt分别为实测概率密度和理论概率密度;N为序列长度。MSD 值越小。表明结果拟合越接近。为直观起见,分别计算矩估计法、最小误差逼近法以及改进遗传算法得到的优化曲线与实测数据的均方差,结果如表1所示。

表1 参数估值与误差Tab.1 Parameters estimation and error
从图6 以及表1 可以看出,采用改进遗传算法所拟合的曲线与真实海杂波分布曲线拟合度较高。
5 结 语
在研究海杂波K分布模型、遗传算法的基础上,针对遗传算法中二进制编码、适应度函数标定存在的缺陷进行改进,并针对早熟收敛问题,采用多种群遗传算法用于参数估计,利用CSIR 组织公布的雷达实测数据进行仿真。仿真结果与统计量估计法以及标准遗传算法进行比较表明,利用改进遗传算法得到的拟合曲线与杂波数据直方图吻合较好,也表明了改进遗传算法用于参数估计的有效性与精确性。
[1]JAKEMAN E,TOUGH R.Generalized K distribution:a statistical model for weak scattering[J].Journal of the Optical Society of America A,1987(4):1764-1772.
[2]胡文琳,王永良,王首勇.基于Zlog(z)期望的K分布参数估计[J].电子与信息学报,2008,30(1):203-205.HU Wen-lin,WANG Yong-liang,WANG Shou-yong.Parameter estimation of compound k distribution model by zlog (z)[J].Journal of Electronics and Information Technology,2008,30(1):203-205.
[3]姜斌,任双桥,黎湘,等.一种新的高分辨雷达杂波模型参数估计方法[J].现代雷达,2007,29(5):14-18.JIANG Bin,REN Shuang-qiao,LI Xiang,et al.Method of high resolution radar clutter model parameter estimation[J].Modern Radar,2007,29(5):14-18.
[4]ANASTASSOPOULOS V,LAMPROPOULOS G A.Generalized radar clutter model[C].Proc.of the IEEE National Radar Conference,1994:41-45.
[5]刘晋胜,彭志平,周靖.一种多策略并行遗传算法研究[J].计算机测量与控制,2011,19(5):118-119.LIU Jin-sheng,PEN Zhi-ping,ZHOU Jing.A multi strategy parallel genetic algorithm research [J].Computer Measurement and Control,2011,19(5):118-119.
[6]BRANKE J,KAUBLER T,SCHMIDTC,et al.A multi population approach to dynamic optimization problems[J].Adaptive Computing in Design and Manufacturing,2000:299-308.
[7]陈国良,王煦法,庄镇泉.遗传算法及其应用[M].北京:人民邮电出版社,1996.CHEN Guo-liang,WANG Xu-fa,ZHUANG Zhen-quan.Genetic algorithm and application [M].Beijing:The People's Posts and Telecommunications Press,1996.
