基于耦合边界元法的水下目标低频声散射特性
2014-12-07魏克难柴应彬
魏克难,李 威,雷 明,柴应彬
(华中科技大学,湖北 武汉430074)
0 引 言
水下复杂目标的声散射特性直接影响着武器装备的水下作战性能,它对于水中目标的识别、隐蔽和反隐身起着决定性作用,一直以来倍受人们的关注,有着重要的军事意义。因此,对复杂目标的散射特性进行精确而快速的预报一直是声学研究的热点之一。目前国内外围绕这个主题,通过研究提出了一系列的理论解法和近似解法,从而对水下目标的声散射特性有了更深入的了解。
目标的声散射问题理论上是解决一个数学物理问题,即求解三维流体空间中的目标受声激励产生的满足波动方程、表面边界条件和辐射条件的散射声场。围绕这个问题,对水下目标声散射特性研究的方法主要分为理论解法和近似解法。理论解法主要包括积分方程法和分离变量法;近似解法主要包括统计能量分析法、T 矩阵法、物理声学方法及时域有限差分法[2-4]。国内外也开发出了很多预报潜艇目标强度的软件,例如瑞典的M.Almgren和M.Nodin[5]开发的SUBTAS 软件,美国海军实验室(NRL)的Joseph Shirron[6]开发的有限元-无限元计算软件SONAX 等。
本文是采取声振耦合边界元的方法,采用商业软件MSC.Patran 建立目标网格模型,采用声学分析软件LMS.Virtual.Lab 进行数值分析计算[7-8],对比探究刚性BeTSSi-Sub和弹性BeTSSi-Sub的全向散射特性,并且通过改变BeTSSi-Sub的外形,探究了在低频段舵和上层建筑潜艇这2个特殊的部分对潜艇目标强度的影响。
1 声学边界元理论
1.1 边界元法简介
边界元法是将问题的微分方程变成边界上的积分方程,然后引入边界上的有限个单元将积分方程离散,得到只含有边界上节点未知量的方程组,然后进行数值求解。由于边界元法是将区域上的控制方程转化为沿着区域边界的积分方程,因此它只需要定义边界上的单元,结合边界条件求解,这样就使处理问题的维数降低一维,可以有效地将复杂的三维几何模型简化为二维图形。与同样复杂的完整三维有限元模型相比,这是更小、易于创建、易于检验,并易于处理的模型,这些简化模型可以在更短的时间内得出结果。但边界元法所建立方程组的系数矩阵稠密,而且一般非对称,矩阵元素分量的计算量很大,增加了计算时间。由于边界元法所利用的微分算子基本解能自动满足无限远处的条件,因而边界元法特别便于无限域以及半无限域问题。
当声波入射物体时,如果结构和流体之间的相互作用比较大,就必须考虑结构和流体之间的相互作用,本文计算弹性体的声散射就属于这一类情况,用到的是基于有限元和边界元相结合的耦合声学边界元理论。
1.2 耦合声学边界元分析理论
运用边界元法处理求解积分方程,边界元需要把边界Ωa离散成许多单元和节点,每个单元内部任意点的声压和法向速度可以用属于这个单元节点上的声压pi和法相速度vni与全局矩阵形函数Na来表示:

式中Na为与边界Ωa上na个节点上声压pi和法向速度vni相关的全局形函数。
在边界元中,还有一些不知道声压和振动速度的节点,例如节点b,也就是ra= rb,则有
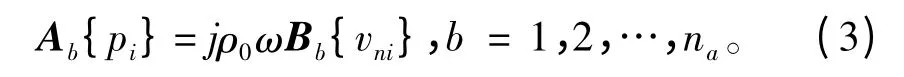
式中系数矩阵Ab和Bb都是(1 × na)的矩阵。
对于耦合边界元,声场分布和结构的振动位移是同时计算出来的。对于边界元网格,可以分为2个部分,一个是与结构网格耦合的部分,包含an1个节点,另一部分是不参与耦合的部分,包含an2个节点(an1+an2= an),这样边界元上的声压p(ra)和速度v(ra)可以写为

式中Na1和Na2分别为与an1节点和an2节点相关的形函数。由于声压也作用在结构上,它作为一个载荷,同样也可以引起结构的振动,这样结构部分的动力学方程为

式中Ks,Cs和Ms分别为结构有限元模型的刚度矩阵、阻尼矩阵和质量矩阵;{ui}为结构移位向量;{Fs}为作用在结构网格上的外载荷(不包含声压载荷);Lc·{pi1}为声压作用在结构网格上的载荷;Lc为(ns× na1)耦合矩阵,即
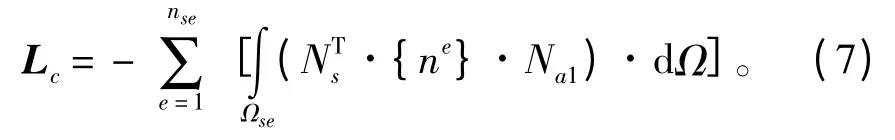
式中:nse为耦合的结构网格的单元数量;Ns为结构网格的形函数;{ ne}为单元的法向方向;负号是因为结构网格的单元法向方向与边界元的单元法向方向相反。
对于耦合边界元法,在结构与声音耦合面Ωs处,结构网格的节点和声音网格的节点需要重合。在耦合面Ωs处,由结构网格的振动速度与声音网格的振动速度的连续性与位移{u}、速度{v}之间的关系{v}=jω{u},可得

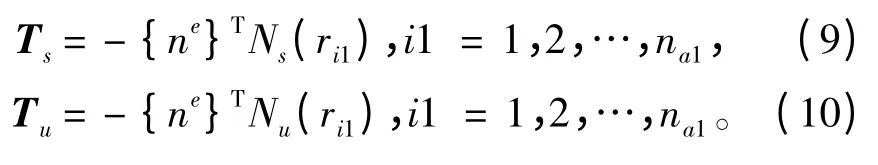
式中{ne}为结构网格的法线方向,负号表示结构的法线方向与声学网格的法线方向相反。将式(8)代入式(3)可得

结合结构有限元方程式(6)和边界元式(11),可以得到结构有限元与边界元的耦合方程为

式中:

2 算例分析
2.1 弹性球壳平面波入射下的散射特性分析
为了验证该方法的有效性,采用此方法计算无界流体中收发合置下弹性球壳的反向散射特性。首先在建立球壳的网格模型,定球壳的外径为1 m,厚度为0.03 m,建立网格模型如图1所示。

图1 球壳的网格模型Fig.1 Shell mesh model
定该球壳的密度ρ = 7 860 kg/m3,杨氏模量E= 200 Gpa,泊松比ν = 0.266。因为是在水中,所以流体参数的设置,密度ρ水= 1 000 kg/m3,声音传播的速度c水= 1 500 m/s,求解平面波入射下的目标强度随频率的变化,与解析解对比分析图如图2所示。
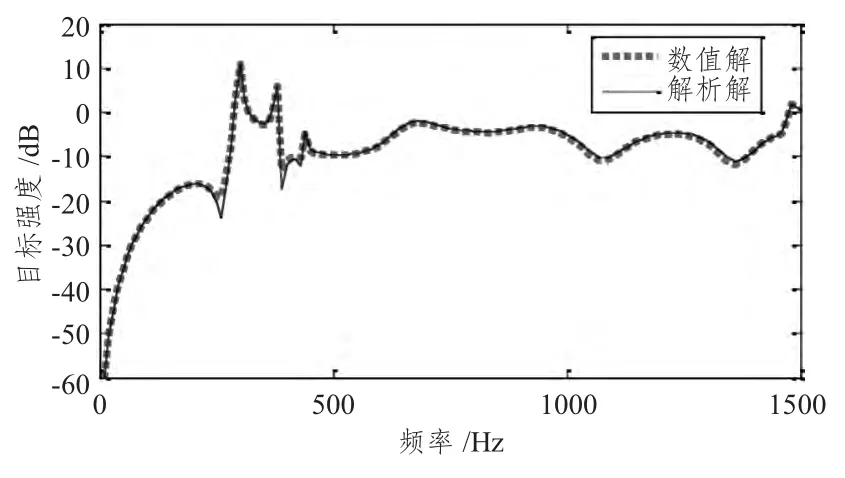
图2 弹性球壳反向散射特性对比图Fig.2 Backscattering of the elastic shell
从图2 可看出,用数值解和解析解有很好的吻合,初步论证了耦合边界元法在计算水下目标声散射特性可行。
2.2 BeTSSi-Sub的全向散射特性分析
按照参考文献[1]中的潜艇规格图 (见图3),在MSC.Patran 中建BeTSSi-Sub的网格模型,如图4所示,此模型有6 656个单元,6 650个节点。
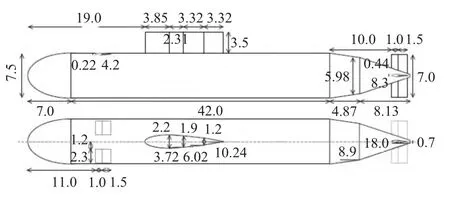
图3 BeTSSi-Sub 规格图Fig.3 Dimensions of BeTSSi-Sub

图4 BeTSSi-Sub的网格模型Fig.4 BeTSSi-Sub mesh model
对于边界元模型来说,要求最大单元的编程要小于计算频率波长的1/6,所以要计算到很高的频率,势必网格单元数量会急剧上升,计算时间会急剧增长,对计算机的要求也变高。所以根据本文所画的网格模型,最大的计算频率约为373 Hz。
从文献[9]可知,潜艇目标强度值的测量随测量距离发生变化,所以为了得到稳定可靠地测量结果,测量应该在远场进行。对于长度为L的潜艇而言,当入射波长为λ,即测量距离r 要大于L2/λ,所以本文定义波源位置为距离潜艇几何中心1 000 m处,计算收发合置情况下刚性和弹性(钢)潜艇的全向散射时的目标强度,定义从潜艇首部入射为0°,从潜艇尾部入射为180°,每隔2°计算1 次,计算频率分别为100 Hz,200 Hz,300 Hz,定义弹性BeTSSi-Sub的材料参数为钢,密度ρ = 7 860 kg/m3,杨氏模量E = 200 Gpa,泊松比ν = 0.266,钢板厚度为35 mm,得到刚性和弹性(钢)的目标强度对比图如图5所示。
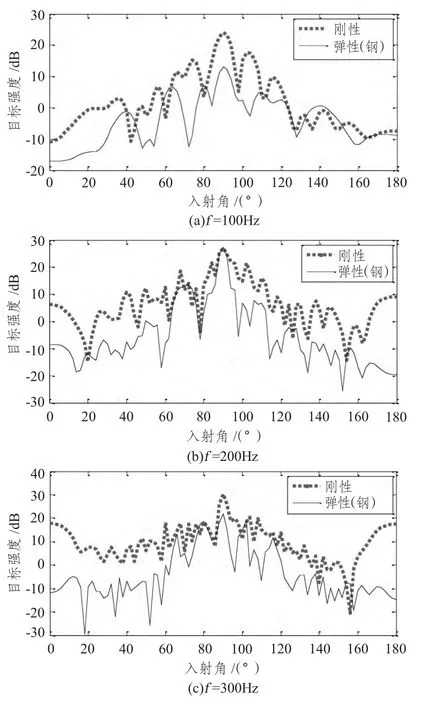
图5 刚性和弹性(钢)BeTSSi-Sub 全向散射目标强度对比图Fig.5 Omni-directional scattering of the rigid BeTSSi-Sub and the elastic (steel)BeTSSi-Sub
从图5 可明显看出,刚性潜艇的目标强度大于弹性(钢)的目标强度,这是由于所谓刚体散射是指物体入射声波的作用下既不发生形变,声波也透不到物体内部,而弹性目标的散射声波则会进入物体的内部,进而会在物体的内部产生更复杂的散射和折射,同时也会引起目标的变形和振动。
2.3 不同形状的弹性(钢)BeTSSi-Sub 散射特性的分析
从潜艇的网格图可以看出,潜艇不是规则的几何体,尤其是舵和上层建筑,因此为了探究这2个形状不规则的部分对潜艇整体目标强度的影响,分别建立无上层建筑的BeTSSi-Sub 网格模型和无舵的BeTSSi-Sub 网格模型,如图6和图7所示。

图6 无上层建筑的BeTSSi-Sub 网格模型Fig.6 BeTSSi-Sub mesh model with no superstructure

图7 无舵的BeTSSi-Sub 网格模型Fig.7 BeTSSi-Sub mesh model with no rudder
从图中可看出,正横方向(90°)是潜艇目标强度最大的方位,一般我们最关心的也是正横附近的目标强度。对这3个不同形状的潜艇网格模型,本文计算了正横方向的反向散射,这3 种模型的材料均为钢,ρ = 7 860 kg/m3,杨氏模量E = 200 Gpa,泊松比ν = 0.266,钢板厚度为35 mm,计算结果如图8所示。
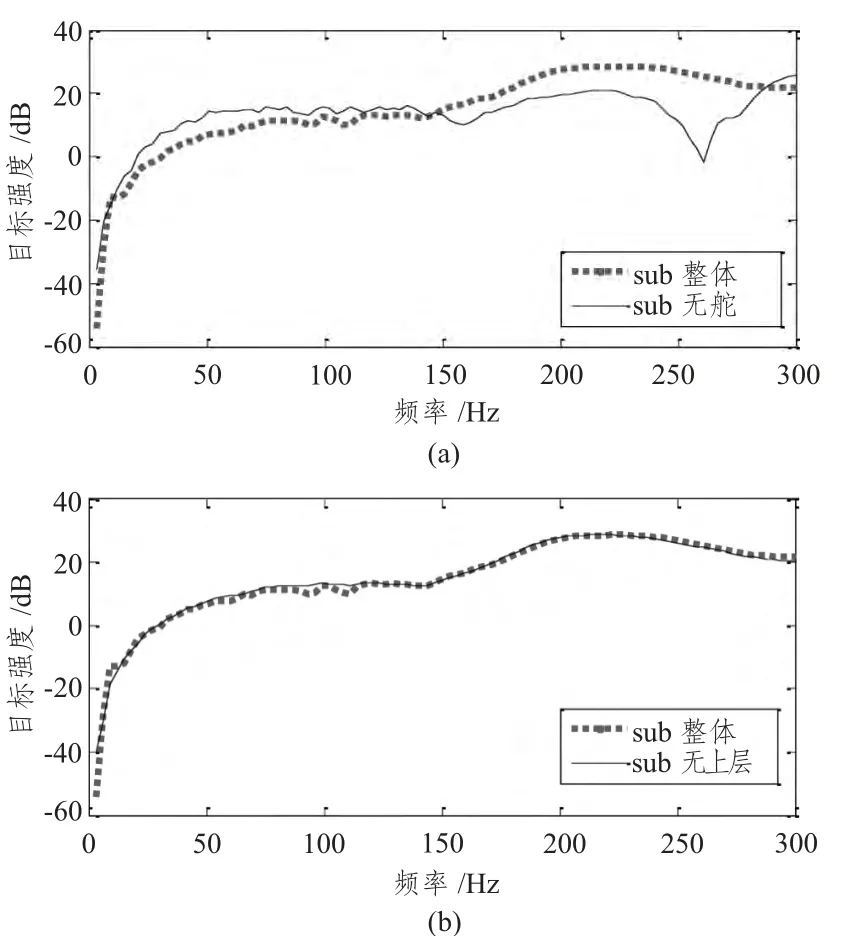
图8 不同形状的BeTSSi-Sub 正横反向散射目标强度对比图Fig.8 Backscattering of the elastic BeTSSi-Sub with different shapes
由图8 可知,在正横方向上,无舵的BeTSSi-Sub 在0~150 Hz的目标强度比BeTSSi-Sub 大,而在150~300 Hz 比BeTSSi-Sub 小。上层建筑的存在对BeTSSi-Sub的目标强度基本没影响,在低频段上,舵对潜艇正横方向目标强度的影响比上层建筑大。
3 结 语
从本文的数值计算算例可以看出,这种结合商业软件的耦合边界元数值计算方法,不仅可以解决简单的弹性目标的声散射特性问题,对于水下像潜艇一样有复杂结构的水下目标,也能准确且成功预报其目标强度。
通过在低频段对不同材料,不同形状的BeTSSi-Sub的目标强度的计算,对比发现:刚性BeTSSi-Sub的目标强度大于弹性BeTSSi-Sub的目标强度;在正横方向上,舵对BeTSSi-Sub 目标强度的影响作用比生层建筑更加明显。
[1]NELL C W,GILROY L E.An improved BASIS model for the BeTSSi submarine [R].Canada;DRDC-AT LANTIC,2003.
[2]李威,赵耀,张涛,等.水下刚硬体声散射场计算及分析[J].声学技术,2007,26(5):844-849.LI Wei,ZHAO Yao,ZHANG Tao,et al.Computation and analysis of the acoustic scattering field from submerged rigid objects[J].Technical Acoustics,2007,26(5):844-849.
[3]汤渭霖.用物理声学方法计算界面附近目标的回波[J].声学学报,1999,24(1).TANG Wei-lin.Calculation of acoustic scattering from object near an interface using physical acoustic method[J].Acta Acustica,1999,24(1).
[4]HASTING F D,SCHNEIDER J B,BROSEHAT S,Afinitedifferenee time-domain solution to scattering from a rough pressure-release surface[J].Acoust.Soc Am,1997,102(6):3394-3400.
[5]ALMEGRON M,NODIN M.Acoustics target strength of submarines.PRAO'S,1991.
[6]SHIRRON J.Computational simulation of elastic scattering[D].Naval Research Laboratory.Washington D.C
[7]龙凯,贾长治,李宝峰.Pratran2010与Nastran2010 有限元分析从入门到精髓[M].北京:机械工业出版社,2011.LONG Kai,JIA Chang-zhi,LI Bao-feng.Finite element analysis from entry to the essence of pratran2010 and Nastran2010 machinery industry press[M].Beijing:China Machine Press,2011.
[8]李增刚,詹福良.Virtual.lab.Acoustics 声学仿真计算高级应用实例[M].北京:国防工业出版社,2010.LI Zeng-gang,ZHAN Fu-liang,Virtual.lab.Advanced acoustic simulation application examples[M].Beijing:National Defense Industry Press,2010.
[9]刘伯胜.水声学原理[M].哈尔滨:哈尔滨大学出版社,2011.LIU Bo-sheng.Water acoustics [M].Harbin:Harbin University Press,2011.
