计及流体效应的三体船流固耦合自振特性
2014-12-07周清华刘世明杜国和
周清华,刘世明,杜国和
(1.江南造船(集团)有限责任公司,上海201913;2.中国舰船研究设计中心,湖北 武汉430064)
0 引 言
如何准确地计算三体船总振动的模态特性,以避开共振状态,是三体船结构设计的关键问题之一。对于三体船在水中的振动问题,需要考虑流体与结构的耦合作用。目前,船舶结构的流固耦合力学分析方法主要有以下3 种:
1)经验公式法如刘易斯图谱法,该方法可求解低阶垂向振动和水平振动的附连水质量,已广泛应用于单体船的振动分析中;
2)解析-数值方法,如Geers 提出的双渐进法[1],该方法适用于研究形状规则的结构;
3)纯数值计算方法[2],如有限元法和边界元法等。
对于形状复杂的水中结构,一般采用数值分析方法,由于该方法在工程上的实用性,国内外学者做了大量的研究。Deruntz 等[3]利用边界积分法计算附连水质量,讨论了处理流固耦合问题的不连续边界积分方法。夏利娟等[4]采用2 种不同边界条件的二维边界元法计算高速船垂向振动的附连水质量。黄晓明等[5]以加筋圆柱壳模型试验为基准,研究船体结构在无限水域中的垂向低阶湿模态特性仿真计算方法;吴绍亮等[6]采用边界元法和经验公式法对船体局部结构的附连水质量计算进行了比较性研究。苏海东等[7]应用有限元-边界元混合法分析了等深度无限大片状域流场中三维结构的自由耦振问题。
本文基于流固耦合振动的纯数值解法理论,分别采取有限元法和边界元法对某三体船流固耦合系统的无阻尼自由振动特性进行比较性研究,并分析侧体附连水质量对三体船总振动特性的影响,为进一步研究受迫耦振问题奠定基础。
1 流固耦合振动的纯数值解法
1.1 流固耦合系统的基本方程
理想不可压缩流体小扰动的动力平衡方程为

式中:▽为Hamilton 算子;p为流场动压力。
边界条件如下:
2)在自由面上(不考虑表面波),p = 0;
3)在固定界面上,∂p/∂n = 0;
结构在流体中的无阻尼自由振动方程为:
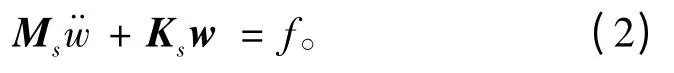
式中:Ms为结构的质量矩阵;Ks为结构的刚度矩阵;w为结构位移矢量;f为流体动压力所产生的节点力矢量。
1.2 有限元法
有限元法将整个流体域离散为若干个流体元,采用Gauss 数值积分法计算各个流体元的贡献。根据Galerkin法建立整个流体域的运动方程为:

式中:H为流体动压力系数矩阵,H = ∭Ω▽N·▽NTdΩ;B为 流 固 界 面 耦 合 矩 阵, B =Λ;Ω为流体域;N为流体元的形函数;Ns为接触面的形函数;Λ为坐标的转换矩阵;=Λ;SI为流固交界面。
由虚功原理得到流固交界面上的流体力矢量为:

合并式(2)~式(4),得到流固耦合系统的运动方程为:

式中:Ma= ρBTB为附连水质量矩阵。
1.3 边界元法
边界元法将船体结构的振动和入射波的作用视为流固交界面上具有分布的脉动源,并离散为有限个源点。定义Green 函数G(P,Q)为Q 点作用一单位脉动源强时在流域内任一点P 处所引起的速度势,则所有界面上的分布源所产生的速度势为:

式中:σ(xs,ys,zs)为流固交界面上单位面积的源强;(x,y,z)为场点;(xs,ys,zs)为源点。
采用Green 函数法计算流场,得到分布源强的积分方程式为:
除上述三种途径的假荫外,唐朝还有杂色荫,其中也有假冒资荫现象。唐朝的前朝荫是对北齐、北周、隋三朝的名臣子孙用荫。贞观元年(627年),唐太宗 “以选人多诈冒资荫,敕令自首,不首者死。 ”〔11〕(p6031)尽管在严刑峻法的管制之下,还是有人诈冒资荫,被发现以后,唐太宗要处以死刑,虽然最后没有实行,但这反映了统治者对于诈冒资荫的厌恶,并且希望通过严惩来告诫其他人。
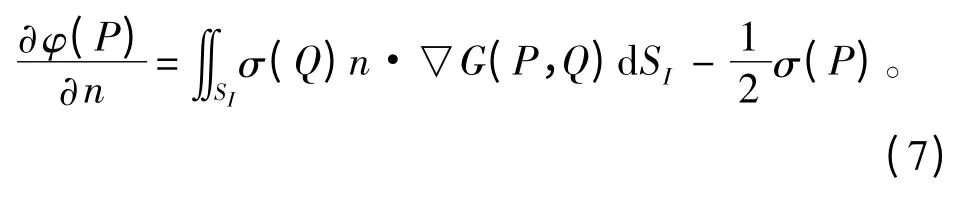
将式(7)通过对边界划分成有限个数的单元进行离散化,可得间接边界积分方程为:

式中C的元素为:

D的元素为:
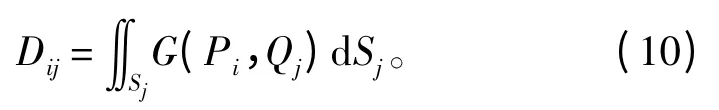
由虚功原理得到流固交界面上的流体力矢量为:

式中A为结构湿表面面积的对角矩阵。
将式(11)代入式(2),得到流固耦合系统的运动方程为:

式中Mf= ρΛTADC-1Λ为附连水质量矩阵。
2 算例及分析
2.1 计算模型

图1 三体船结构有限元模型Fig.1 Trimaran structure finite element model
有限元法中,采用Abaqus 软件计算[8]。对于无限域流场采用Abaqus 提供的三维声学流体单元AC3D4 进行模拟,定义流体介质的压缩模量和密度。水线以下的结构湿表面和水的接触面采用关键字TIE连接,使其始终保持接触状态而不分离。一般情况下模拟无限域流场的边界距结构的距离至少应为结构尺度的6 倍左右,综合考虑计算时间、精度和三体船结构特征,文中将流场半径取为船中距侧体中心距离的5 倍,建立三体船流固耦合计算模型(见图2)。
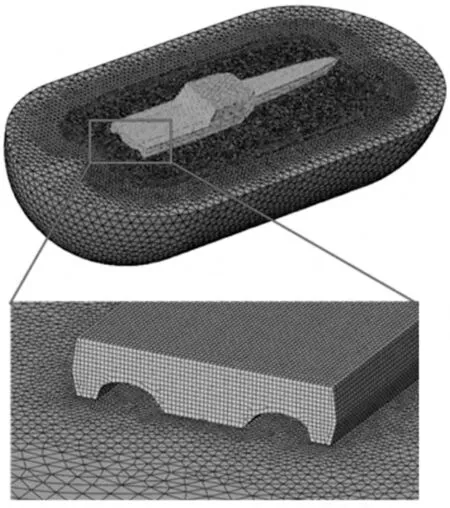
图2 三体船流固耦合计算模型Fig.2 Trimaran fluid-structure coupling calculation model
边界元法中,采用MSC.Nastran 软件计算[9]。定义湿表面网格为流固耦合界面,用边界元代替三维声学流体单元,将无限流域的定解问题简化成仅在流固耦合界面进行数值积分。具体实现过程:在模型数据段,通过卡片MFLUID 定义参考坐标系、液面高度、流固耦合界面、流体密度、是否有对称边界条件、积分方法等参数;通过卡片ELIST 定义构成“湿面”的二维单元,流固耦合界面由一组TRIA3 或QUAD4 单元组成。在情况控制段,通过卡片MFLUID=SID 标识流固耦合分析。
2.2 数值计算
采用Lanczos 算法求解结构的特征值和特征向量,即流固耦合系统的自由振动固有频率和模态。受低阶单元形函数的限制,数值计算结果一般只适用于低频范围。由于文中采用的简化建模方法合理,低阶模态中均为整体振动模态,选取前4 阶典型模态作为研究对象,计算结果如表1所示。
由表1 可见,计及流体效应后的三体船流固耦合自振频率比干模态频率明显降低,其中首阶垂向弯曲和水平弯曲的振动频率降幅最大;与边界元法相比,有限元法的频率计算值均偏小,高阶振动频率相对误差较小,不超过5%。主要原因有2个:一是流场范围对附连水质量的影响[10]。附连水质量随着流场半径的增加而减小,文中采取的流场范围不足以精确模拟无限域流场的影响,致使计算结果偏小;二是流体单元类型、大小和质量对计算结果的影响。
典型振动模态如图3所示。三体船前3 阶总振动模态为垂向弯曲和水平弯曲,高阶模态多为首部水平弯曲和尾部扭转的耦合振动。由于三体船的侧体布置于尾部,首部结构较为瘦削,首部和尾部的抗弯和抗扭刚度差异较大,且剪切中心线和水平弯曲中心线不一致,致使首部水平弯曲与尾部扭转的耦合振动较为突出,该振动特性与普通的闭口类单体船有所不同。
为研究深V型、浅吃水侧体的附连水质量对三体船总振动的影响,现分别考虑侧体和主体附连水质量2 种情况进行比较分析。在MSC.Patran 中,利用卡片MFLUID 可以定义相应的流固耦合界面即可实现计算。计算结果如图4所示。
由图4 可见,仅考虑侧体附连水质量的频率计算值和干模态接近,最大偏差为2.37%;仅考虑主
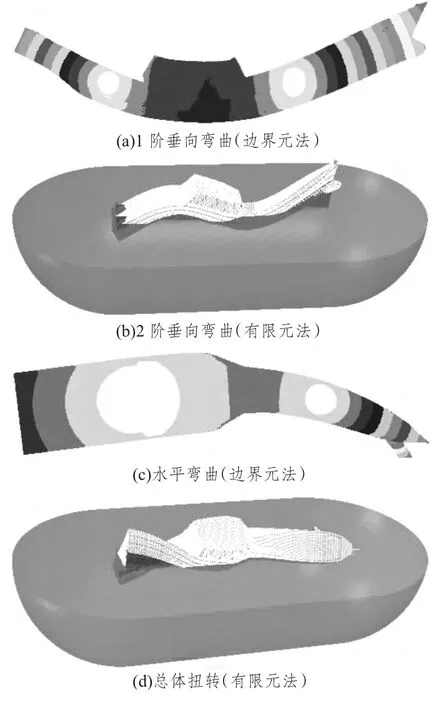
图3 典型振动模态Fig.3 Typical vibration modes

图4 附连水质量的影响比较Fig.4 Additional water mass impact comparison
体附连水质量的频率计算值与湿模态接近,最大偏差为4.85%。由此可知,深V型、浅吃水侧体由于其结构形状独特和排水体积小的特点,其附连水质量对三体船总振动影响很小。
3 结 语
1)考虑流体效应时,三体船自振频率均有所降低,其中首阶固有频率下降幅度最大。
2)三体船总振动较常规船型复杂,需要考虑尾部扭转和首部水平的耦合振动以及连接桥区域的局部结构的耦合振动。同时,由于三体船航速较高,有必要分析螺旋桨和主机激振力作用下的结构振动响应。
3)深V型、浅吃水侧体的附连水质量对三体船总振动的影响较小。在工程应用中,可忽略该类侧体附连水质量的影响。
4)有限元法和边界元法均能解决三体船流固耦合振动问题。相比之下,边界元法降低求解流场问题的空间维数,且自动满足远场辐射条件,单元数少,计算量小,是预报三体船总振动更为快速有效的方法。
[1]GEERS T L.Doubly asymptotic approximations for transient motion of submerged structure[J].The Journal of the Acoustical Society of America,1978,64(5):1500-1508.
[2]陆鑫森.高等结构动力学[M].上海:上海交通大学出版社,1992.
[3]DERUNTZ J A,GEERS T L.Added mass computation by the boundary integral method[J].International Journal for Numerical Methods in Engineering,1978(12):531-550.
[4]XIA Li-juan,WU Wei-guo,WENG Chang-jian,et al.Analysis of fluid-structure-coupled vertical vibration for high-speed ships[J].Journal of Ship Mechanics,2000,4(3):43-50.
[5]黄晓明,朱锡,牟金磊,等.整体结构模型低阶湿模态仿真计算方法[J].舰船科学技术,2011,33(5):9-12.HUANG Xiao-ming,ZHU Xi,MU Jin-lei,et al.Simulation and experimental investigation on transverse lower order wet mode of whole structure model[J].Ship Science and Technology,2011,33(5):9-12.
[6]吴绍亮,金咸定.流固耦合计算方法在船舶局部结构中的应用[J].振动与冲击,2003,22(4):26-28.WU Shao-liang,JIN Xian-ding.Computation method for fluid/structure interaction in local structures of ship[J].Journal of Vibration and Shock,2003,22(4):26-28.
[7]苏海东,黄玉盈,陈琴,等.片状域流场中三维结构的湿频率和湿模态[J].华中科技大学学报,2007,35(1):121-124.
[8]Abaqus/CAE user's manual[DB/CD].2005.
[9]HERTING D N.MSC/Nastran advanced dynamic analysis user's guide[DB/CD].1997.
[10]金占礼,王宗利,李红云,等.结构在无限流体域中的振动时附连水质量的数值计算方法[J].上海交通大学学报,2000,34(8):1078-1082.JIN Zhan-li,WANG Zong-li,LI Hong-yun,et al.Numerical computing method of additional water mass when the structure vibrates in the infinite liquid[J].Journal of Shanghai Jiaotong University,2000,34(8):1078-1082.
