一类特殊的Sturm-Liouville 问题第一特征值的估计
2014-12-07周振宁
周振宁
(天津商业大学宝德学院基础教研室,天津 300384)
一类特殊的Sturm-Liouville 问题第一特征值的估计
周振宁
(天津商业大学宝德学院基础教研室,天津 300384)
为了更精确地研究 Sturm-Liouville 问题第一特征值,本文主要讨论一类特殊的 Sturm-Liouville问题第一特征值关于势函数的依赖性。应用变分原理,估计了此类特殊的 Sturm-Liouville问题第一特征值在不同参数值下的界限,并证明出其中的一些界限是可以达到的,为Sturm-Liouville问题第一特征值的逼近提供了更好的理论基础。
特征值 势函数 极小化序列
Sturm-Liouville问题理论在数学和物理中起着重要的作用,在过去的十几年里许多学者对Sturm-Liouville问题的特征值关于边界的依赖性进行了深入的研究[1-3]。近年来大部分关于 Sturm-Liouville问题的工作都集中在特征值的逼近方面。施德才讨论了自伴常微分算子特征值的解析重数和几何重数的关系[4],王艳基于微分方程基本解,研究了具有光滑势函数的S-L问题特征值和规范常数的高阶渐近式[5],马美绒通过微分方程基本解的高阶展开式,研究了边界条件中含谱参数的Sturm-Liouville算子特征值的渐近展开式.进一步利用初值问题解的渐近估计,并借助于一个积分恒等式,采用留数方法,得到了边界条件中含谱参数的2×2Sturm-Liouville问题特征值的迹公式[6]。
本文研究了类特殊的 Sturm-Liouville 问题第一特征值,估计了此类特殊的 Sturm-Liouville 问题第一特征值在不同参数值下的界限。
考虑Sturm-Liouville 问题

满足边界条件:


其中α为一实数,且α ≠0. 基于变分原则,我们有第一特征值
令

我们来估计

下面得到我们的主要结论.
若 α ≤-1,则
mα=C()α
且Mα= ∞.并且存在函数.使得

这里
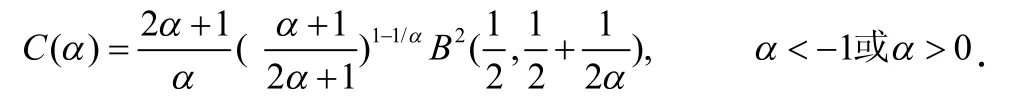
证:令a≤-1,则1≤r<2,根据Ho˙˙lder不等式,有

我们有

所以 m≥1.
考虑一个极小化序列{yk},满足

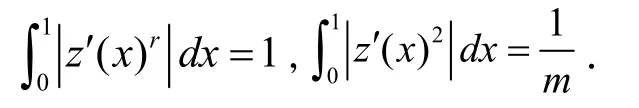
又因为函数z(x)满足欧拉—拉格朗日等式

用z'(x)乘以上述方程并积分,得到
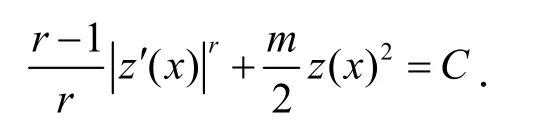
于是得到

做变量替换z=My,我们得到等式

因为

所以
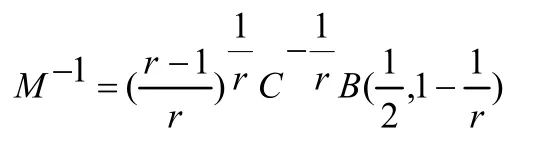
[1]KONG Q, ZETTL A. Eigenvalues of Regular Sturm-LIouville Problems[J].J Differentail Equations,1996,131:1-19.
[2]KONG Q, ZETTL A. Dependence of Eigenvalues of Regular Sturm-LIouville Problems on the Boundary[J].J Differentail Equations,1996,126:389-407.
[3]Rostyslav O.Hryniv,Yaroslav V. Mykytyuk.Inverse spectral problems for sturm-liouville operators with singular potentials,II.Reconstruction by two spectra[J]. North-Holland Mathematics Studies,2005,29:26-37.
[4]施德才.多区间上自伴Sturm-Liouville算子和高阶常微分算子特征值的重数关系[D].南京:南京理工大学,2009:59-102.
[5]王艳.Sturm-Liouville问题特征值的渐近性及其对反问题的应用[D].西安:陕西师范大学,2011:115-152.
[6]马美绒.三类Sturm-Liouville特征值问题[D].西安:陕西师范大学,2013:1-47.
In order to study the first eigenvalue of the Sturm-Liouville problem more precisely, in this paper, a special Sturm-Liouville problem is considered and the dependence of the first eigenvalue on the potential is studied. The boundary of the first eigenvalue with different values of the parameter is estimated and some of them can be get based on the variational principle.It provides a better theoretical basis for the first eigenvalue approximation problem.
eigenvalue potential minizing sequence
