两端锚定的单链聚电解质在交流电场中的滞后效应
2014-12-07吉轩廷
吉轩廷
(北京工业大学,北京 100124)
两端锚定的单链聚电解质在交流电场中的滞后效应
吉轩廷
(北京工业大学,北京 100124)
在均匀的交流电场作用下,应用布朗动力学模拟方法,研究了两端锚定的柔性和半柔性的单链聚电解质的动力学行为。研究结果表明,链段的位置随交流电场的变化表现出类似于磁滞回线的滞后效应,随着交流电的频率减小,这种滞后效应逐渐消失,成为一条单一的曲线。本项目针对两端锚定的聚电解质随交流电场变化的动力学行为的研究,文献中未见报道。
滞后效应 聚电解质 交流电场
1 介绍
近年来,在使用高频率电场操纵聚电解质分子逐步引起关注,特别是关于DNA方面的研究[1-4]。例如,将长度超过7μm的长肌动蛋白丝两端用两个金属电极吸引,终止交流电压后,观察两个电极之间的情况[5]。前人的工作表明,单链PE在交变电场中的构型转变存在滞后性[6]。在聚电解质的动力学和电学行为的研究中,一个单链PE的操纵是至关重要的。与研究链在静态下的行为相比较[7],在外部周期力的扰动下的单链的动力学行为更值得研究[8]。最近一项研究表明[9],通过动态蒙特卡洛模拟,在震荡力下的单链聚合物展现出了周期行和非周期性的动力学行为。在本文中,我们将研究一条两端锚定的柔性或半柔性的PE链,链的两端将处于均匀的交流电场内。通过对链的布朗动力学模拟,我们将研究交流电场的频率对链的位形的影响。
2 模型和方法
我们的系统包括一条单一的线性聚电解质链,处于一个各项均匀的电场中。链的模型为竹簧链模型[10]。该链由N个粒子(单体)构成,由N-1个距离为的键连接。在我们的模拟中,我们假设聚合物链是均匀带电的,每一个分子的带电量均为αe.连接成链的单体具有FENE势能:
其中,r是相邻两个单体之间的键长,bmax是链可以延伸的最大长度,kb为劲度系数。
所有的单体均应满足LJ势:
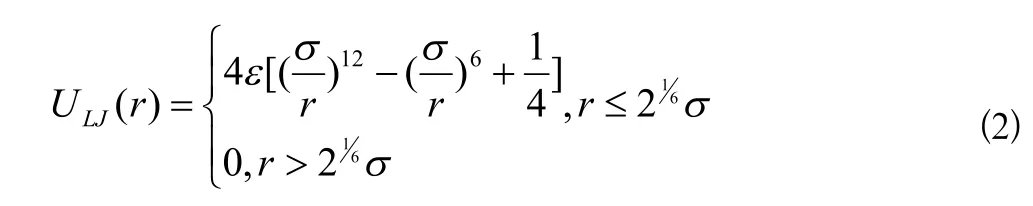
其中,σ仍然反映键长,ε表征了LJ势的强度。因此,单体之间的相互作用是可以忽略的。
该链还将受到因角度改变而引起的势[11,12],

其中,θ是两个单体之间的角度。平衡角度被设置为π,对于半柔性链,弹性系数kθ定为2。粒子之间也会通过库仑势相互作用,该势被写为
由于热浴运动带来的力隐藏在郎之万方程中,
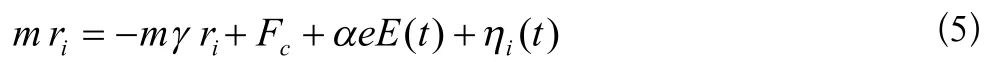

图1
(图1)两端在x轴上被锚定在原点和x=d处的单PE链。交流电场的方向为z轴方向。实点表示链的中点(中间的单体)。
接下来,对于柔性和半柔性PE链,ω 将在一个比较大的范围内变动,我们将研究其对链的中点位置z(t)的影响,以及外部电场E(t)。郎之万方程中的Verlet算法每一步的时间要求为。系统需要先进行710MD时间以达到平衡,并进入静止系统集合(E0,ω),紧接着进行步骤以得到100个粒子的轨迹。
3 结果
三维的柔性和半柔性的PE链如(图2)所示。无论是柔性还是半柔性PE链,都在(z,E)平面内展现了相似的动力学行为。随着频率ω的下降,首先,一些椭圆形曲线出现倾斜,然后,这些曲线的两端逐渐变得平滑。渐渐地,平滑部分不断增多,留在曲线中间部分的圆形越来越小。这意味着,在周期性电场下,曲线中点出现滞后现象。这些滞后现象显示了在交变电场的半个周期内PE链的不同的动力学行为,这也是由于链不能在任何时刻都遵循电场的周期性的变化过程。因此,这显示出了一个在Z和E之间超前或滞后的图像。频率进一步下降将会导致滞后现象的消失。最终,平直的线将完全取代椭圆形曲线。由于半柔性链比柔性链有更大的弹性,因此为了消除半柔性链的这种滞后现象,需要更低的频率。

图2
这种动态变化会在(z,E)平面上以不同的外形反映出来,这主要决定与电场的频率、振幅以及系统其它因素诸如链的长度、固定长度D以及半柔性聚合物链的弹性等的影响。这里,我们只考虑一定系统参数下的结果。如(图2)所示。
(图2)PE链在不同电场频率ω下的轨迹柔性(左图)半柔性(右图)链长度均为。从顶到底,ω依次为:(左图)1/100,1/300,1/900,1/1800,1/5800;(右图)1/100,1/500,1/1400,。Z(t)是链中点随时间变化的位置。
4 结语
总之,本文是首次研究交流电场对两端锚定的单PE链的影响的动力学行为。在空间均匀电场里,不同频率的郎之万动力学模拟表明交流电场的频率是链段空间——电场平面内位形的重要影响因子。一般来说,在低频率段,链会形成一条单一曲线,如其本身形状;在高频率段,链的位形会出现滞后。我们也检验了电场强度对位形的影响,然而,当电场振幅足够低时,对链的形状的影响可以忽略不计。我们希望我们的模拟结果可以被在交变电场下的短链DNA或肌动蛋白检验,并推进聚电解质的动力学和电学行为的研究,更进一步的研究可以解释出一些生物物理学的相关问题。[13,14]
[1]A. E. Cohen, Phys. Rev. Lett. 91, 235506 (2003).
[2]H. Liu et al., Macromolecules, 43, 4805 (2010).
[3]J.-M. Y. Carrillo et al., Macromolecules, 43, 2589 (2010).
[4]P.-Y. Hsiao et al., Soft Matter 7, 1207 (2011).
[5]M. E. Arsenault et al., Biophys. J. 93, L42 (2007).
[6]S. Wang et al., Macromolecules, 43, 7402 (2010).
[7]T. Sakaue, Macromolecules 40, 5206 (2007).
[8]B. Xue et al., J. Chem. Phys. 122, 194912 (2005).
[9]A. K. Chattopadhyayand et al., Phys. Rev. Lett. 98, 088101(2007).
[10]K. Kremer et al., J. Chem. Phys. 92, 5057 (1990).
[11]Y. F. Wei et al., J. Chem. Phys. 127, 064901 (2007).
[12]Z. Ou et al., J. Chem. Phys. 123, 074905 (2005).
[13]B. Xue et al., J. Chem. Phys. 119, 7534 (2003).
[14]B. Xue et al., Int. J. Mod. Phys. B 18, 2123 (2004).
We investigate the dynamics of a single flexible and semiflexible polyelectrolyte (PE), fixed at both ends under the action of spatially uniform alternating-current (ac) electric fields using Brownian dynamics simulations. The results show that the shapes of the orbits in the position-electric field plane are strongly influenced by the frequencies of ac electric field. These orbits transform gradually from hysteretic cycles to single curves with the decreasing frequencies.
Hysteresis effect Polyelectrolyte Ac electric field
