基于正交试验－遗传神经网络的陶瓷球面精密磨削参数优化

刘 伟 邓朝晖， 万林林 伍俏平

1.湖南大学，长沙，410082 2.湖南科技大学，湘潭，411201

0 引言

陶瓷等难加工材料以其强度高、耐高温、耐化学腐蚀等优良性能在工业和国防等重要领域应用广泛。随着科技的迅速发展，各种高精度复杂曲面形状零件的需求日益迫切，这对磨削加工的精度和效率提出了更高的要求。目前，陶瓷等难加工材料的精密加工主要通过超硬精细磨料的研磨及精密磨削来实现［1］。

传统的球面磨削主要采用三种加工方法［2－4］：一是用平行砂轮外圆磨削球面，采用这种加工方法磨头需要安装在回转盘上，对回转盘的精度与响应要求较高；二是采用成形砂轮磨削球面，这种加工方法效率虽高，但存在砂轮修整时间长、砂轮磨损后加工形状精度低等问题；三是用碗型砂轮内侧磨削球面，该方法常用于小直径的球面磨削，加工过程中需要大量磨削液进行润滑冷却。

当前磨削加工所面临的共同问题是严重依赖操作人员的经验，选择磨削加工工艺方案的方式仍以传统的试切法和经验法为主，加工效率低，加工柔性差［5］。由于磨削加工成形机理复杂，影响加工的因素众多，加工参数在线检测困难，故磨削加工过程的工艺方案优选一直是困扰制造企业的难题。如何实现磨削加工质量的整体提升，实现磨削加工经济效益的最大化及磨床加工能力的最大利用，即在保证最佳工件质量的前提下实现磨削加工效率的最大化、磨削加工成本的最小化是亟待解决的问题。

本文针对氮化硅陶瓷材料球面廓形工件砂轮法向跟踪精密磨削，采用正交试验法设计试验，运用极差法和方差法综合分析砂轮半径、砂轮转速、进给速度、磨削厚度等工艺参数对工件表面粗糙度、加工时间的影响规律；在此基础上利用改进遗传神经网络算法（genetic neural network，GNN）优化砂轮半径、砂轮转速、进给速度、磨削厚度等工艺参数。

1 陶瓷球面精密磨削加工方法

采用MK2945C高精度数控坐标磨床，对氮化硅陶瓷材料球面廓形工件进行砂轮法向跟踪精密磨削。如图1所示，配合自旋工作台，用弹性夹头夹持工件的柄部，通过磨床的C轴、U 轴、Z轴及自旋工作台之间的联动，采用工件旋转、砂轮沿圆周进给的方法实现氮化硅陶瓷材料球面廓形工件的磨削加工［6－7］。其中，砂轮轴和主轴之间存在一个偏置D，其大小为砂轮半径rs、球头半径rw、磨削余量Ar之和；通过U轴控制，无需额外设置砂轮半径补偿。磨削过程中，砂轮轴与工件轴相互垂直，通过C轴旋转，磨削点与砂轮中心连线始终与球面廓形工件法线方向（即径向）重合；砂轮在轴线方向（即Z向）做上下往复运动，同时高速旋转，保证砂轮外圆周表面磨粒能均匀地参与磨削，最大限度地减少砂轮损耗，提高砂轮耐用度。

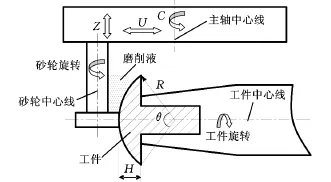
图1 陶瓷球面廓形工件砂轮法向跟踪精密磨削示意图

2 陶瓷球面精密磨削加工正交试验

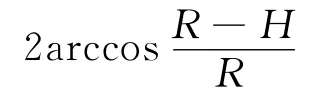
为实现氮化硅陶瓷材料球面廓形工件精密磨削，需要合理选择磨削加工工艺方案。根据上述分析，影响工件质量的工艺参数有砂轮半径rs、砂轮转速ns、进给速度vr、工件转速nw、磨削厚度ap和砂轮Z向插磨速度vZ等。其中，工件由自旋工作台驱动旋转，nw不可调，取100r／min；vZ取固定值11m／min。采用正交试验法设计氮化硅陶瓷材料球面廓形工件精密磨削试验，rs、ns、vr、ap都取3个水平，分析各工艺参数对工件加工质量和加工效率的影响，各因素及其水平如表1所示。为确定加工效率，取磨削总厚度aT为6μm。从正交表中选择标准的4因素3水平正交表L9（34），设计试验方案，并分别测量9组试验后工件表面粗糙度Ra与加工时间t，进行正交试验极差与方差分析。其中加工时间t只考虑实际加工过程，工件装夹等辅助时间不计算在内，其计算公式为

式中，aT／ap为加工循环次数；π／3为球头角度θ的一半；tj为进刀时间，取3s；ta为球面磨削完后横向继续加工时间，取2s；tt为退刀时间，取5s。

表1 正交试验各因素与水平

每组试验加工3次，Ra取3次加工的算术平均值。正交试验数据与极差计算结果如表2所示，方差计算结果如表3所示。其中，响应P是指正交试验中各因素对结果的影响百分比，用于改进工艺参数遗传神经网络优化。

表2 L9（34）正交试验数据与极差计算

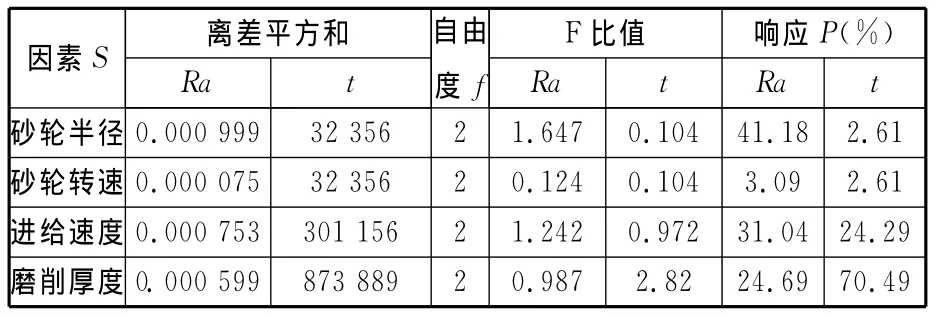
表3 L9（34）正交试验方差分析

3 GNN优化算法

神经网络算法的网络结构能够良好地实现具有相关性的已知条件与结果之间的多重非线性映射关系，但是优化过程中易于陷入局部最优［8］。遗传算法是一种全局优化搜索算法，能够避开局部最优。由基于马尔可夫链的定量数学证明可知，简单遗传算法不是全局收敛的，带有最优保存的遗传算法才会全局收敛［9］。为此引入自适应遗传算法（adaptive genetic algorithm，AGA）。在进化过程中，AGA根据个体的具体情况自适应地改变交叉概率Pc、变异概率Pm，保持多样性，防止早熟收敛，提高算法的计算速度与精度。结合BP（backpropagation）神经网络算法和AGA的特点，建立改进GNN优化算法，能够实现全局高效寻优。

改进GNN优化过程如下：使用遗传算法对神经网络结构的权值阈值初始种群进行进化学习，得到最优的权值阈值基因，从而建立具有相关性的已知条件与结果之间的多重非线性映射关系，具体流程如图2所示；将已知条件输入神经网络，计算出结果。其中，遗传算法的目标函数是权值阈值基因个体代入相应结构的神经网络后，该网络所有学习样本的计算结果与理论结果的误差之和。

图2 改进GNN优化算法学习流程图

由于影响磨削加工质量的因素繁多，影响因素之间又相互交叉、相互制约，故确定最佳磨削工艺方案较为困难。采用人工智能技术，建立磨削加工要求与工艺参数之间的多重非线性映射关系，确定磨削工艺方案，优化工艺参数，能够实现高效精密磨削。氮化硅陶瓷材料球面廓形工件精密磨削工艺参数优化采用改进GNN算法。

氮化硅陶瓷材料球面廓形工件精密磨削中，加工目标是在满足一定表面粗糙度的情况下实现高效加工。由上述分析可知，需要优化的工艺参数有砂轮半径、砂轮转速、进给速度和磨削厚度。考虑到磨削工艺参数存在非连续取值的问题，直接采用遗传神经网络优化算法计算得到的工艺参数与实际取值有差距，无法直接应用，且对相关参数进行调整后无法保证加工质量和加工效率；因此，还需要建立磨削工艺参数与加工要求的预报模型，保证调整后的工艺参数能够满足加工要求。优化流程如图3所示，当工艺参数无法根据实际取值继续进行调整且不能满足要求时退出循环，无结果输出。

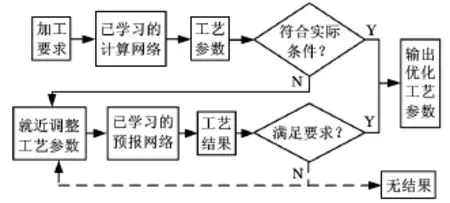
图3 氮化硅陶瓷材料球面廓形工件精密磨削工艺参数优化流程图

建立两个网络模型：其一用于计算磨削工艺参数，其二用于预报加工质量与效率。采用2输入4输出、4输入2输出的神经网络结构，网络隐层均取1层，节点数可由下式计算得到：

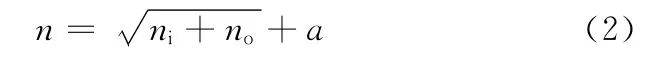
式中，n为隐层节点数；ni为输入节点数；no为输出节点数；a为1～10之间的常数。

根据式（2）并通过程序比较寻优确定n＝12。即神经网络模型结构为2×12×4、4×12×2，如图4所示。其中，xi、yj（i，j＝1，2，3，4）分别表示神经网络的输入与输出值。

图4 神经网络结构图

每个神经元的输出f可由下式计算：

式中，i、j分别为神经元、输入变量的个数；pj为输入变量；wij为权值；b为阈值。

为进一步提高改进GNN的优化速度与精度，结合正交试验分析结果对其进行改进，在对网络进行学习前用方差分析响应P替换工艺参数所在层神经元的权值wij。

4 试验验证

由于建立的神经网络结构输入输出较小，正交试验的9组数据可以作为GNN的学习样本。经过GNN学习，得到遗传神经网络陶瓷球面精密磨削参数优化模型（包括计算与预报两个模型）。应用该优化模型，进行了5组氮化硅陶瓷材料球面廓形工件数控磨削试验。5组试验的磨削加工条件同前，加工目标见表4中输入部分。通过GNN陶瓷球面精密磨削参数优化模型的计算，得到加工参数的试验计算值，具体输入输出见表4。其中，输入x1、x2分别表示表面粗糙度、加工时间，输出y1、y2、y3、y4分别表示砂轮半径、砂轮转速、进给速度、磨削厚度。

表4 GNN陶瓷球面精密磨削参数优化输入输出

其中第5组试验在现有试验条件水平下无法实现，需调整输入的表面粗糙度或者加工时间的要求。采用上述工艺条件与工艺参数进行氮化硅陶瓷材料球面廓形工件数控磨削加工。磨削加工完成后，采用JB－4C精密粗糙度仪检测氮化硅陶瓷材料球面廓形工件的表面粗糙度，检测结果见表5。加工时间可以通过式（1）计算得到。

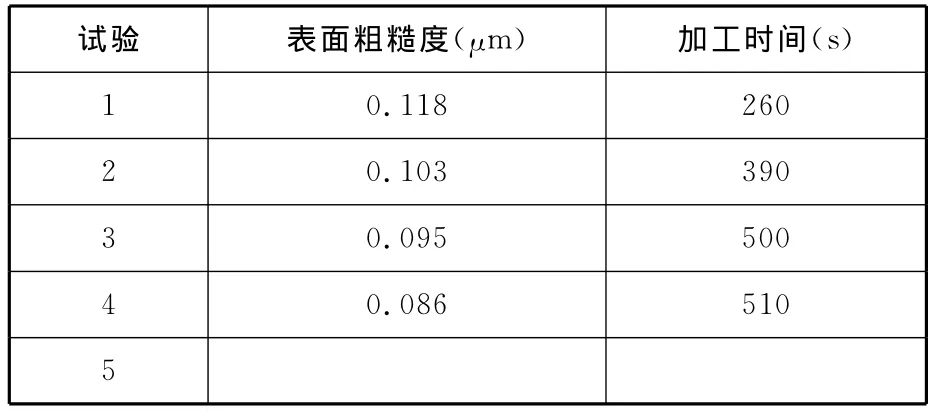
表5 陶瓷球面精密磨削加工检测结果

比较表4、表5可知：工件实际表面粗糙度值均比加工目标的对应值小，且都满足加工时间的要求，表明加工目标确实得到了优化，加工质量得以提高；表面粗糙度目标值和检测结果基本相等，误差小于5%。由此可知，本文所建立的优化计算模型能够有效地应用于氮化硅陶瓷材料球面廓形工件数控磨削加工参数的优化计算，提高了加工质量与加工效率。

5 结论

（1）针对氮化硅陶瓷材料球面廓形工件砂轮法向跟踪精密磨削，建立了基于正交试验－遗传神经网络的陶瓷球面精密磨削参数优化计算模型，该模型通过确定加工目标与加工参数之间的非线性近似函数关系，实现加工参数优化计算，且易于编程实现。

（2）采用正交试验法设计氮化硅陶瓷材料球面廓形工件砂轮法向跟踪精密磨削试验，运用极差法和方差法综合分析砂轮半径、砂轮转速、进给速度、磨削厚度等工艺参数对工件表面粗糙度、加工时间的影响规律。分析结果显示：砂轮半径为15mm、砂轮转速为17 000r／min、进给速度为4.58mm／min、磨削厚度为1μm时，工件表面粗糙度较低；进给速度为9.16mm／min、磨削厚度为3μm时，加工时间较短，加工效率较高。各工艺参数对表面粗糙度的影响程度从大到小依次为砂轮半径、进给速度、磨削厚度、砂轮转速，各工艺参数对加工时间的影响程度从大到小依次为磨削厚度、进给速度。

（3）设计改进GNN基本结构模型，利用该算法建立陶瓷球面精密磨削参数优化计算模型，并应用于氮化硅陶瓷材料球面廓形工件砂轮法向跟踪精密磨削试验。试验结果表明，该优化计算模型是有效和可靠的，有利于陶瓷球面精密磨削加工质量和加工效率的提高。

［1］Malkin S，Hwang T W.Grinding Mechanisms for Ceramics［J］.CIRP Annals－Manufacturing Technology，1996，45（2）：569－580.

［2］Yin Ling，Vancoille E Y J，Lee L C，et al.Highquality Grinding of Polycrystalline Silicon Carbide Spherical Surfaces［J］.Wear，2004，256（1／2）：197－207.

［3］牟仲德，陈云.一种实用简便的球面磨削方法［J］.工具技术，2005，39（12）：79.Mou Zhongde，Chen Yun.A Practical and Easy Method of Spherical Grinding［J］.Tool Engineering，2005，39（12）：79.

［4］Li Dongdong，Xu Mingming，Wei Chenjun，et al.Error Analysis and In－process Compensation on Cup Wheel Grinding of Hard Sphere［J］.International Journal of Machine Tools and Manufacture，2011，51（6）：543－548.

［5］Liao T W，Chen L J.A Neural Network Approach for Grinding Processes：Modelling and Optimization［J］.International Journal of Machine Tools and Manufacture，1994，34（7）：919－937.

［6］邓朝晖，李约铃，万林林，等.基于砂轮法向跟踪的回转曲面磨削研究［J］.制造技术与机床，2011（2）：86－89.Deng Zhaohui，Li Yueling，Wan Linlin，et al.Research of Revolving Curved Surface Grinding Based on Normal Tracing of Wheel［J］.Manufacturing Technology ＆ Machine Tool，2011（2）：86－89.

［7］Deng Zhaohui，Wan Linlin，Zhang Xiaohong，et al.Modelling the Processing Parameters of Rotary Curved Surface Grinding Using RSM［J］.Advanced Materials Research，2011，338：130－135.

［8］于兰峰，关立文，黄洪钟.基于神经网络的多目标优化模型的模糊解法［J］.中国机械工程，2001，12（z1）：131－133.Yu Lanfeng，Guan Liwen，Huang Hongzhong.Fuzzy Multi－objective Optimization Methods Based on Functional－link Network［J］.China Mechanical Engineering，2001，12（z1）：131－133.

［9］石峰，娄臻亮，张永清，等.基于遗传算法和神经网络的冷挤压工艺参数模糊优化设计［J］.机械工程学报，2002，38（8）：45－49.Shi Feng，Lou Zhenliang，Zhang Yongqing，et al.Fuzzy Optimization of Cold Extrusion Mold Based on Genetic Algorithm and Neural Network［J］.Journal of Mechanical Engineering，2002，38（8）：45－49.