剪式机构阵列可展结构的静力学分析方法与应用研究
2014-12-05刘国林王三民
刘国林 王三民 尚 鹏
西北工业大学,西安,710072
0 引言
可展结构是一种由收缩状态展开成预先设定的展开状态、承受载荷并保持稳定构型的结构,因具有可收缩、可展开的特点,在航空、航天和建筑领域具有广阔的应用前景。可展结构可以看成是由某种类型的单元机构按照某种方式阵列而成,这是这种机构式结构不同于于其他结构的一个显著特点。
随着可展结构的广泛应用,许多学者在从事其构型设计、运动及动力学分析等方面的研究工作。土耳其学者Gokhan等[1]以曲柄滑块机构为对象进行运动拓扑分析,发现了一种剪式单元机构构成环状可展结构和多面体可展结构的方法。雅典学者Charis[2]采用剪式机构构成了平面和曲面可展结构,研究了其展开过程中的几何非线性现象和杆件的变形。Karpov等[3-4]根据有限元理论,采用离散傅里叶变换,研究了不同单元构成的阵列组合结构的边值问题,并进一步研究了因构件尺寸误差产生的构件的初始装配应力的概率分布问题。Stephen[5]利用传递矩阵法研究了阵列组合结构在不同的载荷和支撑下的弹性静力学问题。EI-Raheb[6]根据周期对称理论,研究了剪式机构构成的六边形可展结构的动力学特性,获得了各阶固有频率和阵型。杨毅等[7]利用凝聚矩阵法,进行了剪式单元可展结构的静力学分析与拓扑优化设计。陈向阳等[8]利用主从自由度分析了剪式单元的真实力学模型,并推导了混合坐标下剪式单元的刚度矩阵和自由振动方程。张春等[9]进行了空间可展机构弹性动力学特性研究。
可展结构的单元多、尺寸大,如果按照常规的有限元方法对其进行建模和分析,计算量大,效率低,耗时长。所以,如何在分析中有效地利用可展结构由一个基本单元按照某种方式阵列而成的结构特点,减小模型计算量,提高计算效率,成为目前研究的一个热点。本文以剪式单元机构线状阵列可展结构为研究对象,建立其静力学分析有限元模型,根据总刚度矩阵的循环特性,通过离散傅里叶变换进行求解,得到了该类型可展结构各铰链处的位移和约束力。因阵列组合可展结构的总刚度阵总可以通过简单的变换而变成循环矩阵,所以该方法也可推广应用于其他类型的可展结构中。该方法是进行阵列组合结构静力学分析的一种新方法。
1 建模方法
剪式单元线状阵列可展结构如图1所示。该类可展结构以剪式机构作为单元机构,相邻剪式机构之间铰接连接,通过线状阵列,得到N个剪式单元组成的平面可展结构,各剪式单元机构编号分别为0,1,…,N-1,各铰链点编号为i0、j0、k0,…,iN-1、jN-1、kN-1,iN、jN。

图1 剪式机构线状阵列可展结构
1.1 剪式单元刚度阵
剪式单元机构如图2所示,由两根杆通过中间的枢轴节点铰接构成,展开角度用θ表示。由于相邻的剪式机构之间铰接,而每个剪式单元机构有6个节点,分别为A、B、C、A′、B′、C′,故可将剪式机构划分为4个两节点平面梁单元,分别为单元AB、BC、A′B′、B′C′。根据梁单元刚度阵及其在整体和局部坐标系下的转换关系,组装剪式机构的4个梁单元,可得到整体坐标系下剪式单元的刚度矩阵和平衡方程。对于图2b所示的剪式单元,常用于环状阵列可展结构,其单元刚度矩阵的建立稍有不同。

图2 剪式机构单元
由于节点B、B′铰接,所以其平动自由度相等,即xB=xB′、yB=yB′,代入剪式单元的平衡方程,得

式中,f*、q*为16×1的列向量,分别为各节点处的节点力和位移;k*为对应刚度阵。
节点A、C、A′、C′的外部力矩为0,可以释放其转动自由度,节点B、B′是单元机构的内部节点,不与其他单元机构直接发生联系,可以凝聚其自由度。根据保留自由度和被凝聚的自由度,式(1)分块表示为

其中,qr、f*r分别表示保留自由度及其对应的力或力矩,为8×1的列向量,qo、f*o分别表示被凝聚的自由度及其对应的力或力矩,同为8×1的列向量。krr、kro、kor、koo为矩阵k*的分块表示,无特殊含义。保留自由度为节点A、A′、C、C′的两个平动自由度分量。由式(2)得凝聚后的平衡方程:

式中,kr为剪式机构单元的刚度阵。
1.2 总刚度矩阵
将式(3)所得的剪式单元刚度矩阵进行组装,得到总刚度矩阵K,平衡方程为

式中,F、q分别为节点力和位移矩阵。
由于相邻剪式单元之间铰接,所以有

将式(5)代入式(4),最后得平衡方程:

其中,qr(r=0,1,…,N-1)为4×1的列向量,各分量分别为剪式单元r中节点A、A′的两个平动自由度分量,qN分量分别为剪式单元N-1中节点C、C′的两个平动自由度分量,Fr(r=0,1,…,N)为对应于qr的载荷,矩阵K*的各分量由前述计算过程确定。
将边界条件代入式(6),得到一个静定线性方程组,求解该方程组,可得到各节点的位移。但是当剪式单元机构数量较多时,刚度矩阵K*的规模会很大,导致计算量增加,计算效率降低。可展结构由剪式机构线状阵列构成,结构上规律性较强,刚度矩阵K*也具有较强的规律性,这是该类结构刚度矩阵不同于普通结构的一个显著特点,该特点为求解式(6)提供了新的方法。
1.3 平衡方程的卷积形式
式(6)中,矩阵K*的第2行至第N行是循环的形式,下面通过等价变形,将矩阵K*表示为循环矩阵。
式(6)可以展开表示为


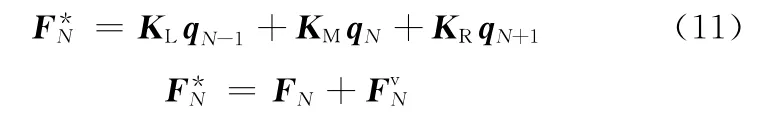

综合式(8)、式(10)、式(11)得式(6)的等价方程组,表示成离散卷积的形式为

1.4 环状可展结构的有限元模型
以上为剪式机构线状阵列可展结构的有限元模型的建立过程,当进行环状阵列时,因坐标变换矩阵不同,使得总刚度阵不是循环矩阵,这时,采用以下方法处理。
环状可展结构如图3所示,单元机构如图2b所示,每个单元机构对应的圆心角都是α。对每一个剪式单元建立固定坐标系XrOYr,O点位于圆心,OYr轴过铰链点ir、jr。仍然划分为4个单元AB、BC、A′B′、B′C′,对应6个节点 A、B、C、A′、B′、C′。整体位移的选择遵循以下原则:剪式单元r的节点A、B、A′、B′的整体位移以坐标系XrOYr为参考系,节点C、C′的整体位移以坐标系Xr+1OYr+1为参考系,从而保证不同剪式单元中的同一个梁单元的坐标变换矩阵相同。
按照前述过程,组装整体坐标系下的梁单元刚度矩阵,并进行自由度凝聚,可得到剪式单元的刚度矩阵。上述整体自由度选择原则保证了不同的剪式单元具有完全相同的刚度矩阵。组装剪式单元的刚度矩阵,可得到可展结构的总刚度矩阵。由于单元0与单元N在铰链i0、j0处铰接,所以总刚度阵为循环矩阵,无需进行式(12)所示的变换过程。另外,需要说明的是,载荷向量F的各分量应表示在与对应自由度相同的坐标系下,即剪式单元r的节点A、B、A′、B′的载荷表示在坐标系XrOYr中,节点C、C′的载荷表示在坐标系Xr+1OYr+1中。最后可得式(12)所示的卷积形式的有限元方程。

图3 剪式机构环状阵列可展结构
2 求解方法
式(12)将剪式机构线状阵列可展结构的有限元方程表示为离散卷积的形式,离散傅里叶变换和离散卷积的性质为求解该方程组提供了新的方法。式(12)本质上仍是一个非齐次线性方程组,其通解可以表示为一个特解和对应的齐次线性方程组的通解之和。
2.1 F(n)=q(n)*K(n)的特解
首先将F(n)、K(n)、q(n)进行拓展,使其成为周期性无限长序列,即

式(12)的另一种等价形式为

对式(14)两边进行离散傅里叶变换,然后在等式右侧同时乘以和除以e-i2πsp/(N+1),得

由式(15)得

对式(17)进行离散傅里叶逆变换得

q(s)即为所求得的位移。






由式(22)、式(23)得


因此,式(12)的特解可以表示为

2.2 q(n)*K(n)的通解


对式(27)进行离散傅里叶逆变换得


式(29)即为q(n)*K(n)=0的通解。
以上求得了式(12)的特解及其对应的齐次线性方程组的通解,根据非齐次线性方程组的解的结构及式(25)、式(29),式(12)的通解可以表示为

2.3 计算各铰链点位移和约束力
式(12)的通解可以表示为式(30)的形式,但是,式中系数向量C以及F(0)、F(N)未知,所以,需进一步计算系数向量C和F(0)、F(N)。
由式(30)可得

将式(31)代入式(19),并根据F(N)=FN+FvN,得到一个静定线性方程组,解之,得F(0)、F(N)、q(N)。
得到F(0)、F(N)后,代入式(25),可得各铰链点的位移q(s),其中s=1,2,…,N-1,将q(s)代入式(3),得到各剪式单元中节点 A、A′、C、C′的节点力,减去各节点处的外部载荷,得到各铰链点的约束力。另外,根据自由度凝聚过程,还可以求得各铰链点B、B′的位移和约束力。得到各节点的位移后,在单元的局部坐标系下,与几何矩阵相乘,得到各单元的应变,与应力矩阵相乘,得到各单元的应力。
3 算例


表1 直线阵列结构铰链点C、C′的位移 mm

表2 直线阵列结构节点B、B′的最大应力 MPa
例二为环状阵列可展结构,5个单元机构,约束i0、j0处x、y方向位移,单元2、3的节点B、B′处受到100N的径向力作用,其余条件同例一。计算结果如表3、表4所示。比较计算结果可以发现,环状可展结构的应力和变形远小于直线可展结构。

表3 环状阵列结构铰链点C、C′的位移 mm

表4 环状阵列结构节点B、B′的最大应力 MPa
4 结论
(1)本文根据有限单元法,将剪式单元机构划分为四个平面梁单元,通过对其自由端和铰接点自由度进行凝聚,建立了剪式单元机构的刚度矩阵,然后组装剪式机构的刚度矩阵得到可展结构的总刚度阵和有限元方程。通过等价变形,将总刚度阵表示为循环矩阵,平衡方程表示为离散卷积的形式。
(2)根据离散傅里叶变换和离散卷积的性质以及非齐次线性方程组解的结构,提出了一种新的方法求解平衡方程,得到了各单元的变形和应力,以及各铰链点的约束力,最后采用两个算例验证了方法的有效性。
(3)由于阵列组合结构在结构上的循环对称的特点,文中所用方法不仅适用于剪式机构阵列形成的可展结构,也适用于其他类型的单元机构阵列形成的各种形式的可展结构。该方法相对于常规的有限元方法,计算量减小了,提高了计算效率。
[1]Gokhan K,Eres S,Ozgur Kisisel A U.A Family of Deployable Polygons and Polyhedra[J].Mechanism and Machine Theory,2008,43:627-640.
[2]Charis G.An Improved Analytical Model for the Prediction of the Nonlinear Behavior of Flat and Curved Deployable Space Frames[J].Journal of Constructional Steel Research,1997,44(1/2):129-158.
[3]Karpov E G,Stephen N G,Dorofeev D L.On Static Analysis of Finite Repetitive Structures by Discrete Fourier Transform[J].International Journal of Solids and Structures,2002,39(16):4291-4310.
[4]Karpov E G,Stephen N G,Liu W K.Initial Tension in Randomly Disordered Periodic Lattices[J].International Journal of Solids and Structures,2003,40(20):5371-5388.
[5]Stephen N G.Repetitive Beam-like Structures:Distributed Loading and Intermediate Support[J].International Journal of Solids and Structures,2009,46(20):3664-3668.
[6]EI-Raheb M.Modal Properties of a Cyclic Symmetric Hexagonal Lattice[J].Computers and Structures,2011,89(23/24):2249-2260.
[7]杨毅,丁希仑.剪式单元可展机构静力学分析与拓扑优化设计[J].中国机械工程,2010,21(2):184-189.Yang Yi,Ding Xilun.Analysis and Topology Optimization of Deployable Mechanism Based on Pantograph[J].China Mechanical Engineering,2010,21(2):184-189.
[8]陈向阳,关富玲,陈务军.折叠结构的主从自由度分析[J].工程力学,1999,16(5):83-88.Chen Xiangyang,Guan Fuling,Chen Wujun.Master/Slave Freedom Analysis for Foldable Structures[J].Engineering Mechanics,1999,16(5):83-88.
[9]张春,王三民,袁茹.空间可展机构弹性动力学特性研究[J].机 械 科 学 与 技 术,2007,26(11):1479-1482.Zhang Chun,Wang Sanmin,Yuan Ru.On Elastodynamic Characteristics of Space Deployable Mechanism[J].Mechanical Science and Technology for Aerospace Engineering,2007,26(11):1479-1482.
