涡旋柱面垂直度误差评定算法研究

胡瑢华 王 轮 陈中扬 刘国平

南昌大学，南昌，330031

0 引言

决定涡旋压缩机诸多优良性能的关键点在于涡旋齿的加工精度。为了评价涡旋齿加工精度的高低，本文就涡旋齿柱面数据进行分析，从垂直度的角度来判断涡旋齿柱面的加工性能。

国内外诸多学者从事着垂直度方面的研究工作。如，Peng等［1］提出了基于实数编码的多种群遗传方法评定轴线对平面的垂直度；Lai等［2］和Wen等［3］也同样用遗传算法以及遗传优化算法评定了圆柱面的垂直度；侯宇［4］提出了采用非线性约束最优化算法评定三坐标上测量线对面垂直度的方法；朱振伟［5］采用光学技术研究了垂直度误差测量系统。以上研究对于涡旋齿柱面垂直度误差的研究具有参考价值，但是由于其研究的垂直度均为线对线、线对平面、平面对平面以及圆柱面对平面，且使用的遗传算法、光学技术以及非线性约束最优化模型较为复杂，不易实施，因此，上述方法难以在工业上进行广泛运用。针对涡旋齿柱面的特殊形状，本文提出基于最小二乘的逼近优化算法来评定涡旋齿柱面垂直度，并将结果与ZEISS测量仪测量的结果进行比较。

1 涡旋型柱面的产生

用具有螺旋状的涡旋型线构成具有一定厚度的动静涡旋齿，并使动静涡旋齿之间满足正确啮合，这一过程称为涡旋齿型线的生成［6］。本文中的涡旋齿型线采用法向等距法生成［7］。涡旋柱面则是以该型线为准线，平行于Z轴的直线为母线所形成。该渐开线方程为

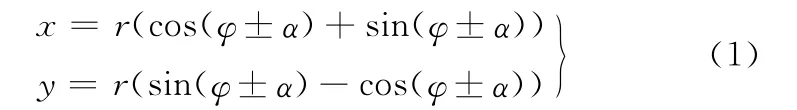
式中，r为基圆半径；φ为渐开线渐开角；±α为内外涡旋准线的起始角。

2 建立数学模型

垂直度误差属于相对位置误差，柱面对基准平面相对位置关系及精度要求如图1所示。

2.1 基准平面的确定

设基准平面上点的坐标为 Qi（xi，yi，zi），i＝1，2，…，m，基准平面方程为

则基准实际面上各采样点Qi对基准平面的偏差为

根据最小二乘法原理，令偏差平方和最小，即可表示为

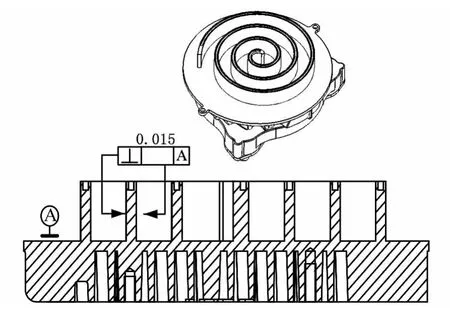
图1 涡旋齿外形及其垂直度要求

将式（3）代入式（4）进行展开，分别对a、b、c求导且令S·a＝0，S·b＝0，S·c＝0，采用矩阵法求取a、b、c的值，基准平面即可确定。同时可知该基准平面的法向量为v＝ （a，b，－1），该平面与理想XOY平面的夹角为γ，则

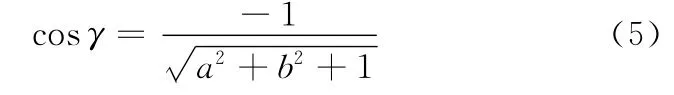
2.2 逼近参数的求取

设涡旋型柱面的实测数据为P＊i（x＊i，y＊i，z＊i），i＝1，2，…，n，将该实测点数据向基准平面投影，投影点的坐标为P′i（x′i，y′i，z′i）。由于基准平面方程已知，且该平面的法向量v＝ （a，b，－1），则投影线方程为

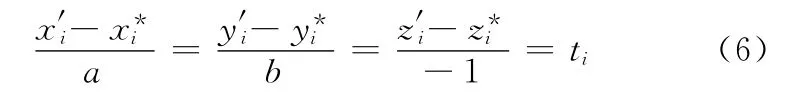
式中，ti为任意非零实数。

将式（6）中的x′i、y′i、z′i的表达式代入到式（3）可求得

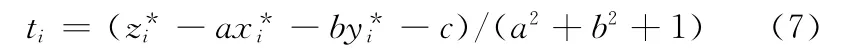
于是各实测点P＊i（x＊i，y＊i，z＊i）到基准平面的投影点Pi（xi，yi，zi）的值分别为

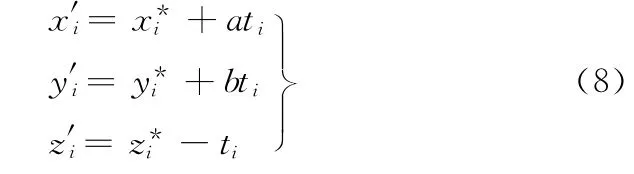
如此即可将涡旋型柱面上的点投影到基准平面上，将三维问题转化为二维问题来计算。由于式（2）是建立在XOY平面内的理想方程，而基准平面并不一定与该平面重合，因此为了方便计算，需要将基准平面的点再次投影到理想平面，设投影点坐 标 为 Pi（xi，yi，zi），则 xi＝ x′i，yi＝ y′i，zi＝0。

将实测点投影到理想平面后，即将三维垂直度的问题转化为二维平面上的点到涡旋线之间的距离问题，可将此距离进行反投影后来表示涡旋型柱面的垂直度误差。

将式（2）表示平面曲线设为Π，那么可以将Π看成是相应的柱面f（x，y）＝0与平面z＝0的交线。在Π充分光滑的情况下，Π上任意一点的特征可以用下面两个矢量来表示：矢径p，单位法矢量n，切线矢量τ。

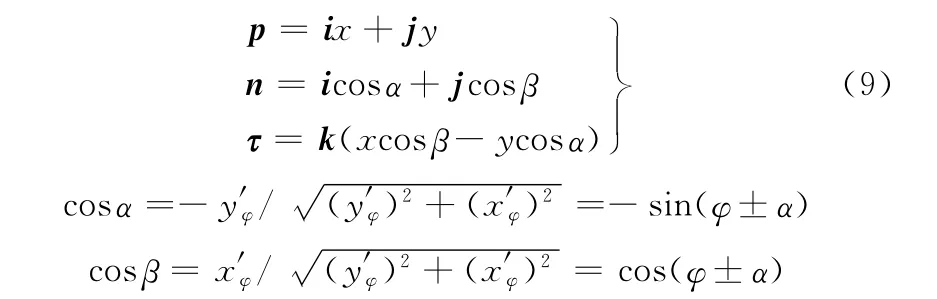
由于实测点P＊i（x＊i，y＊i，z＊i）投影到XOY平面的坐标为Pi（xi，yi），均在理想曲线Π 附近，设理想曲 线 Π 上与点Pi（xi，yi）相对应的 点 为Pφ（xφ，yφ），该点的切向量为m，法向量为k，如图2所示。

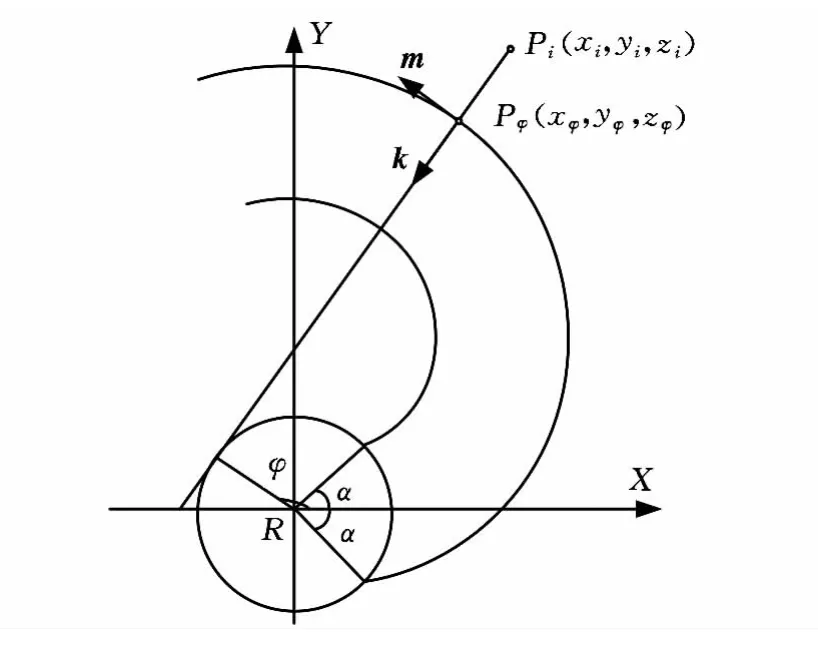
图2 涡旋型柱面在XOY平面投影

根据理想方程的数学特性，对渐开线方程中的x、y求导，即可求得m ＝ （x′φ，y′φ）。由于向量m与向量k相互垂直，那么k＝ （－y′φ，x′φ）。将向量k单位化后可得到k的单位向量，即可得到理论曲线上渐开角为φ的点在向量k方向上的梯度为

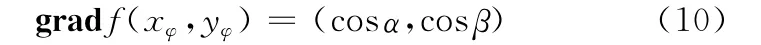
对于涡旋线，定义影响函数［8］为

设Pi（xi，yi）与其对应的理论点 Pφ（xφ，yφ）之间形成的向量为f，则f可以表示为

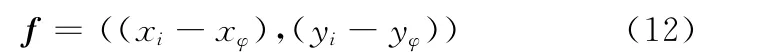
向量f方向与k的方向相反。那么Pi（xi，yi）到理想曲线Π的距离的第一部分可以表示为

将式（10）与式（12）代入到式（13），即可得到垂直度误差的第一部分距离的详细公式：

为了减小由于设计基准、加工基准和测量基准不重合带来的误差，提高算法精度，评定时需要进行微量调整。针对本文中的涡旋柱面，微量调整包括两个方向上的微分移动量δx、δy与绕一个轴的微分旋转量θz［8］。设u＝ （δx，δy，θz）T为逼近参数，并用它来描述曲线的位置和姿态。设Pi（xi，yi）经过微量调整后的坐标为P＃φ（x＃φ，y＃φ），那么P＃φ与Pi之间的关系［9］为

通过式（15）可知，Pi（xi，yi）到理想曲线Π的距离与逼近参数u及P＃φ（x＃φ，y＃φ）到理想平面的距离两个因素相关，记

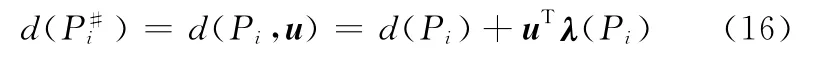
其中，d（Pi）为点到曲线的距离：

根据最小二乘原理求取逼近参数u，令

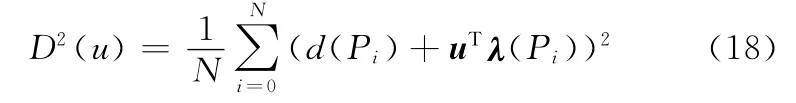
为了求出式（18）的最小值，需要对逼近参数u的各个分量进行求导，即对δx、δy、θz求导，并令其为0。将求导的3个式子进行整理可得如下等式：

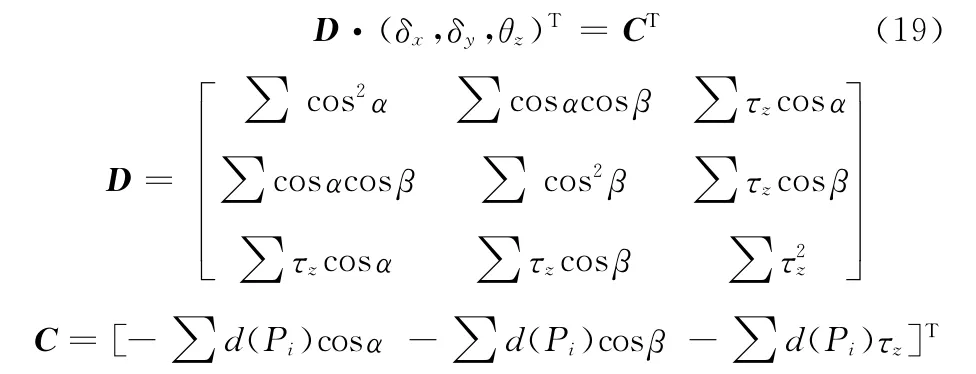
利用以上整理出来两个矩阵即可以求出逼近参数u。

2.3 垂直度的计算

将u代入式（16）得到：

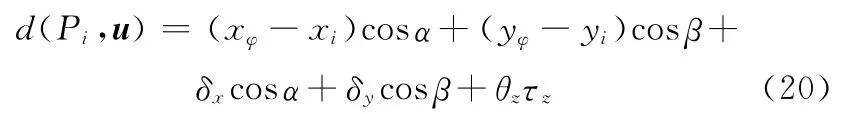
利用式（20）即可求出每个实测投影点Pi（xi，yi）到理想曲线Π的距离，设这些数据中最大值与最小值之差为e′，即

由于e′是每个XOY理想平面上投影点到理想曲线Π的距离，为了反映实测点到涡旋柱面的真实距离，需要将e′进行反投影，设反投影后的距离为e。由式（5）可知理想平面与基准平面的夹角为γ，那么

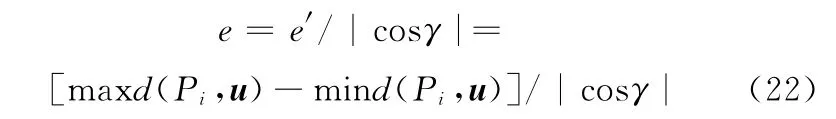
以式（22）的结果来表示涡旋型柱面对底面的垂直度误差。

在此特别提出，DuT＝CT的解法按照线性方程组的原始定义解法（即用CT取代D中的某列求解某未知数的方法）较uT＝D－1CT的解法精度高。

3 算法测试与分析

3.1 数据来源与数据格式

本文数据来源于德国ZEISS公司UMC 550型的三坐标测量机。被测的涡旋盘及三坐标探头与涡旋齿相对位置如图3所示，探头的运动轨迹如图4所示。

图3 涡旋齿与探头相对位置示意图

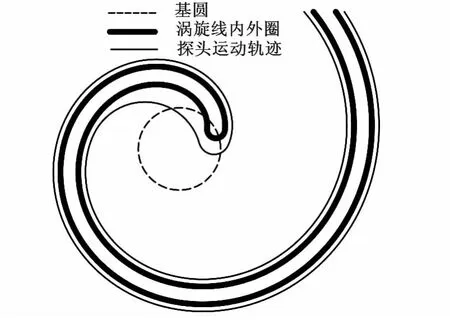
图4 型线与探头的检测轨迹俯视图

图3中，三坐标测量机的探头（扫描式）置于高度1上，外圈从外到内，内圈从内到外，贴着涡旋齿面行走，探头中心的移动轨迹为图4中的虚线所示。在探头运动的过程中采集高度1上的1000个数据点。同理，在高度2和3上进行同样的数据采集工作，这样得到三圈的数据经过ZEISS预处理后导出的数据便是本文的数据来源。

本文所使用的数据为某型号涡旋压缩机静盘涡旋齿内圈与外圈数据，以内圈数据为例，其格式以及部分数据见表1。表1中R－N，A－N，H－N分别为数学模型上的理论点的极半径、极角、高度；R、A、H分别为实测点的极半径、极角、高度。

3.2 测试结果与分析

德国ZEISS公司UMC 550型号的三坐标测量机作为本文的比较对象，其性能参数如表2所示。

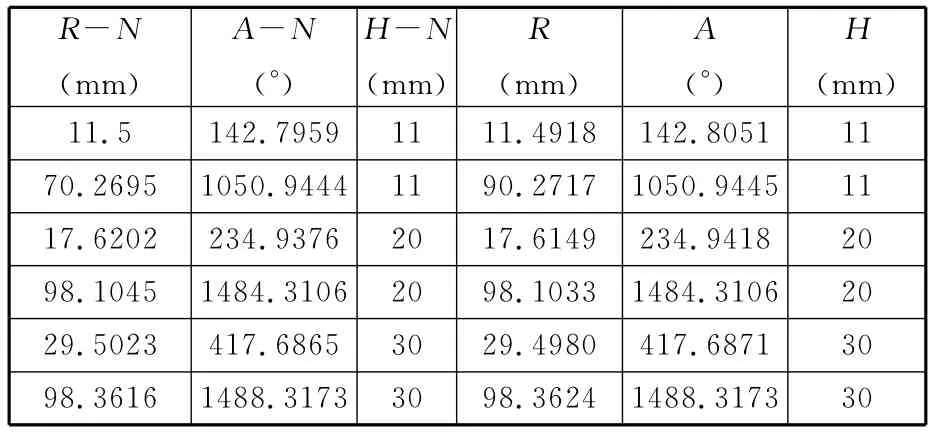
表1 静盘内圈部分数据及格式

表2 UMC 550型三坐标性能参数表

就采集到的静盘内外涡旋齿面数据为例，通过ZEISS三坐标测量机的计算，每个点到理想柱面的距离组成的曲线如图5和图6所示。

图5 静盘内圈ZEISS计算结果曲线图

图6 静盘外圈ZEISS计算结果曲线图

图5与图6中横坐标表示数据点的个数Ni，纵坐标表示距离di，di值精确到微米级，变化范围均在－8～8μm之间，由此可知ZIESS的算法精度很高。

将同样的数据导入本文算法程序中，其运行结果的数据曲线如图7和图8所示。

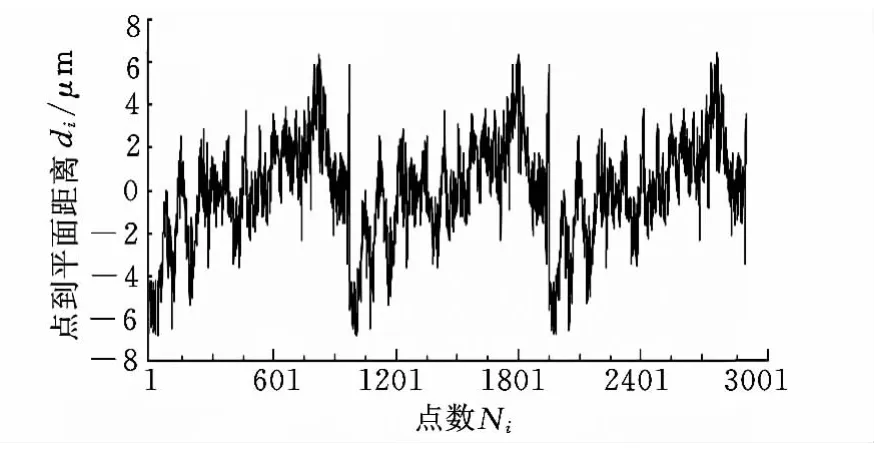
图7 静盘内圈本文算法计算结果曲线图

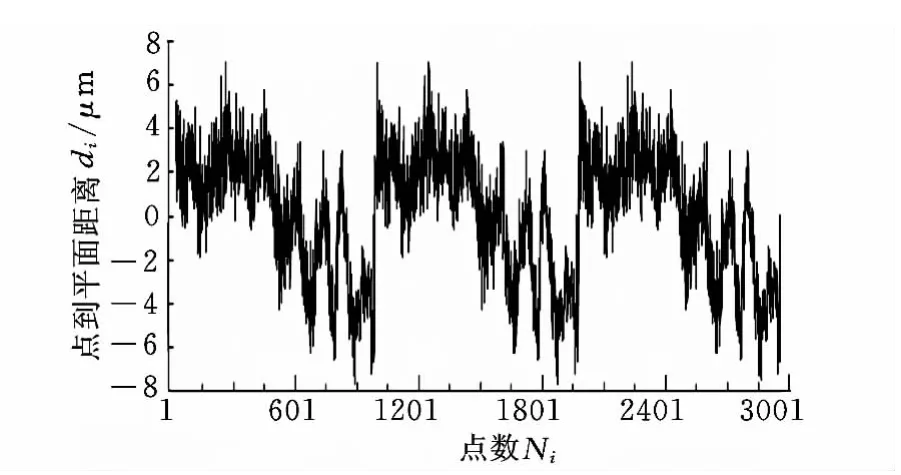
图8 静盘外圈本文算法计算结果曲线图

将图5与图7进行比较，本文算法结果曲线走势与ZEISS计算结果曲线走势完全一致，若将两条曲线放在一张表中进行重合度比较，可以发现本文算法结果曲线与ZEISS算法结果曲线重合度在99%以上，这表明本文算法具有与ZEISS算法相同的精度。经过图6与图8的重合度比较，可得到相同的结论。为了说明重合度的问题，本文将部分数据点在本文算法中的结果与在ZEISS的结果进行比较，如表3所示。

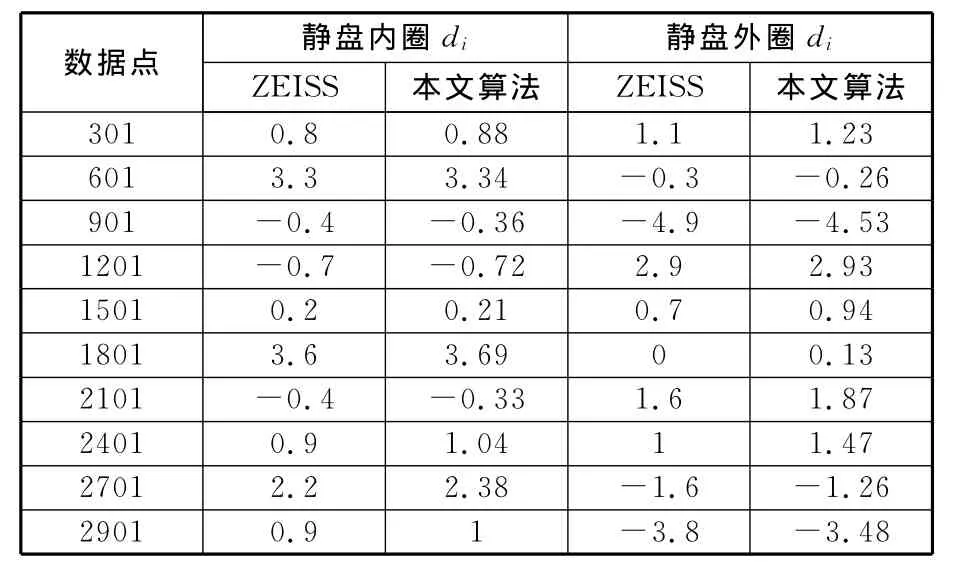
表3 点到柱面距离结果比较 μm

表3为相同的数据在两种不同算法中结果，可发现结果极其相近，差值仅微米之间，完全可以认为两点重合。涡旋柱面垂直度误差在两种算法中的最终结果如表4所示。

表4 垂直度误差结果比较 μm

通过表4的结果比较可知，本文算法与ZEISS算法结果基本相同，说明了本文算法的准确性。

4 结论

本文根据涡旋面的形成原理，基于最小二乘的逼近优化算法建立了评定涡旋面垂直度误差的数学模型，并将算法予以编程实现。通过大量的数据对该算法进行测试，结果表明：本文算法的结果曲线图与ZEISS的结果曲线图走势完全一致，重合度达到99%以上，精度可达到微米级。该算法可作为涡旋齿柱面垂直度的评定算法。

［1］Peng J，Zhong Y R，Huang M F.Perpendicularity Error Evaluation of an Axis Based on New Generation GPS［C］／／2009Third International Conference on Genetic and Evolution Computing.Guilin，2009：85－88.

［2］Lai H Y，Jywe W Y.Precision Modeling of Form Errors for Cylindricity Evaluation Using Genetic Algorithm［J］.Prec.Eng.，2000，24（4）：310－319.

［3］Wen X L，Song A G.Cylindricity Error Evaluation Based on an Improved Genetic Algorithm［J］.Acta Metrologica Sinica，2004，25（2）：115－118.

［4］侯宇.三坐标测量机上平行度和垂直度的精确评定［J］.计量学报，1994，15（3）：232－234.Hou Yu.The Exact Evaluation of Parallelism and Perpendicularity on Coordinate Measuring Machine［J］.Acta Metrologica Sinca，1994，15（3）：232－234.

［5］朱振伟.垂直度误差测量系统的软件开发［D］.武汉：华中科技大学，2009.

［6］Yu Chen，Nils P H，Eckhard A G.Mathematical Modeling of Scroll Compressors－Part I：Compression Process Modeling［J］.International Journal of Refrigeration，2002，25：731－750.

［7］胡瑢华，刘强飞，宋红滚，等.涡旋压缩机型线的加工及其误差分析［J］.南昌大学学报（工科版），2012，34（1）：79－82.Hu Ronghua，Liu Qiangfei，Song Honggun，et al.Profile Processing of Scroll Compressor and Its Error Analysis［J］.Journal of Nanchang University（Engineering ＆ Technology），2012，34（1）：79－82.

［8］熊有伦.精密测量的数学方法［M］.北京：中国计量出版社，1989.

［9］全荣，杨泰来.计算机辅助复杂曲面轮廓度误差评定的通用数学模型［J］.国防科技大学学报，1992，14（4）：86－92.Quan Rong，Yang Tailai.A General Mathematic Model of Computer Aided Evaluating Profile Error of Complex Surfaces［J］.Journal of National University of Defense Technology，1992，14（4）：86－92.