衍射光栅机械刻划工艺理论分析与实验研究

张宝庆 史国权 石广丰 蔡洪彬

长春理工大学，长春，130022

0 引言

衍射光栅是航空、军工等领域光谱仪器的核心元件。机械刻划加工方式［1］在制作低刻线密度原刻衍射光栅方面具有独特的优势。它是利用金刚石刻划刀在镀有金属膜（如铝膜）的基底上进行挤压、抛光，形成光栅槽形的过程［2－3］。

光栅机械刻划已有近200年的历史。目前，世界上光栅刻划技术领先的是法国、德国、美国和日本等发达国家，其机械刻划光栅工艺先进，光栅品质已经接近极限。国内衍射光栅机械刻划工艺方法仍与几十年前相同——正式刻划前需要通过多次、长时间的试刻划，并且在刀具设计与刻划时加入经验值进行槽形补偿［4－5］，才能获得合格品。这导致成本高、浪费大，机械刻划槽形无法预控。近年来，国内外许多学者针对刻划机、金刚石刻划光栅理论、金刚石［6］刻刀晶面定向与刃磨工艺等开展了研究，并取得了阶段性成果，但尚未有针对刻划工艺与槽形预控的研究报道。

光栅刻划中，铝膜材料变形是几何非线性与材料非线性的问题，而有限元模拟分析技术是解决复杂工程技术问题的有效途径，故将材料试验与有限元模拟技术相结合是研究光栅刻划槽形预控的有效方法。对光栅刻划成槽工艺过程的研究结果表明：光栅成槽与刀具结构参数、工艺及安装参数（统称为工装参数）关系密切，因此需要一种有效的方法，即通过预先设定正确的工装参数来实现对槽形的预控。

1 刻划过程分析与转化

1.1 刻划工装参数与槽形参数的定义

1.1.1工装参数的分析与确定

金刚石尖劈刀刀具结构如图1所示，它由2个前刀面（定向面和非定向面）、1个后刀面、1条主刻划刃和2条副刻划刃构成，是一个以刀尖为基点，具有“三面三刃”的空间三棱锥结构。由此建立刀具正交参考坐标平面，如图2所示。

在此坐标系下定义刀具结构参数：

（1）刀尖角——在正交平面内测量的刀具定向面与非定向面之间的夹角。

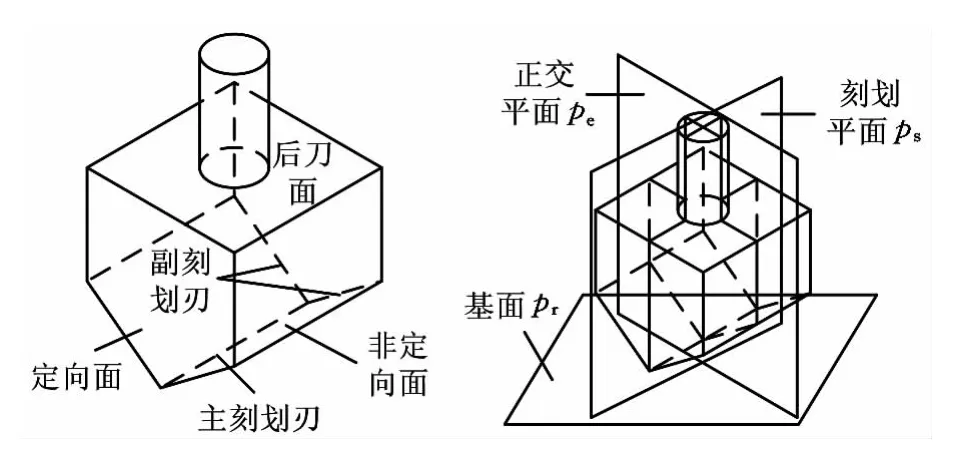
图1 尖劈刀刀具几何结构 图2 刀具正交参考平面

（2）定向角——在正交平面内测量的刀具定向面与基面间的夹角。

（3）俯仰后倒角——在倒角平面内测量的刀具后刀面与基面间的夹角。

（4）滚转后倒角——在基面内测量的后倒角面的法平面与刻划平面之间的夹角。

（5）刃口半径——磨制刀具时，3条刃上产生的圆角半径。

刀具安装参数：

（1）滚转角——绕刻划平面与基面相交轴旋转产生的角度。

（2）俯仰角——绕正交平面与基面相交轴旋转产生的角度。

（3）方位角——绕刻划平面与正交平面相交轴旋转产生的角度。

（4）刻划速度——刻划过程中，刻刀单位时间内的行进距离。

（5）落刀深度——刻划刀刀尖点距离薄膜表面的垂直距离。

1.1.2槽形参数的定义

图3为衍射光栅机械刻划示意图，刻划后理想的槽形各参数用图4表示。图4中，φ为槽底角；θ1为闪耀角；θ2为非闪耀角，θ2＝180°－θ1－φ；d为光栅常数；b为槽宽；h为槽深。

图3 衍射光栅机械刻划示意图

由于实际刻划的槽形截面与理想槽形截面不一致，所以实际槽形各参数的度量采用“主要近似法”或“加权平均法”对槽形作几何近似，将代表槽形的主要结构作为度量对象，或将槽形主要结构与次要结构作加权平均后作为度量对象。本文根据光栅刻划的实际情况，采用“主要近似法”对槽形参数进行描述。

图4 理想化槽形参数示意图

1.2 刻划工艺理论分析与过程转化

利用高倍率显微镜对刻划后的光栅端面及截面进行观测，发现两端没有材料挤出的现象（图5），多个光栅槽形截面的重合性好（图6）。从两端无材料挤出且多个槽形截面重合性好可知，刻划过程中不产生切屑，几乎没有材料沿纵向流动，光栅刻划过程可近似认为是铝膜受刻划刀挤压，薄膜材料向两侧隆起的过程。

图5 高倍显微镜下刻划光栅始、末端面图

图6 原子力显微镜光栅多截面槽型

刀具在刻划光栅行进过程中，在铝膜上形成三角槽形。经过刀尖点沿刻划方向取铝膜任意截面C（图7），当刻刀沿刻划方向进给至L1时，刻刀在截面C上投影的三角形高为H1。同理，进给至L2时，高为H2。依此类推，当刻划深度不再变化时槽形截面投影的三角形高便是刻划深度。由此，便可将刻划过程转化为楔形片压入过程，将三维刻划转化为二维平面应变问题。

图7 光栅刻划截面成型原理示意图

1.3 光栅刻划实际截面投影求解分析

初始建立的坐标系如图8所示，以OX轴正方向为刻划刀行进方向，在正交平面OYZ上投影：角A为定向角。OP为初始定向面在OYZ上的投影，当刀具经过安装参数俯仰角α、滚转角β、方位角θ调整后，定向面在OYZ上新的投影为OP′，新定向角为A′。

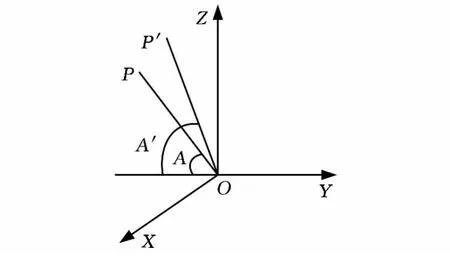
图8 光栅截面定向面投影位置图

根据OP 的方向余弦（0，cos A，sinA），可求得

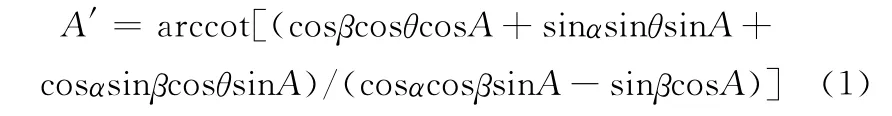
从式（1）可知，光栅刻划实际截面投影与定向角、俯仰角、方位角、滚转角的函数关系，通过调整其中几个参数，便可得到新的投影位置与截面形状。

2 光栅机械刻划过程有限元模拟

2.1 材料力学参数的获取

为了进行有效、准确的光栅刻划数值模拟试验，须对刻划成槽有较大影响的力学参数如弹性模量、金刚石与铝薄膜的摩擦因数等进行准确测量。

这里以79线／mm中阶梯衍射光栅刻划模拟实例为参照，对6.5μm厚铝薄膜样本做纳米压痕与划痕实验，图9为纳米压痕实验图，横坐标为纳米压头压入深度（位移），纵坐标是压头压入力的大小（载荷）。图10为纳米划痕实验图，横坐标为划针划入铝薄膜时间，纵坐标分别为法向力、横向力及它们对应的位移。表1所示为多次重复试验分别得到的弹性模量E、金钢石刻刀与铝薄膜间摩擦因数的平均值。根据文献［7－10］，运用量纲理论、反演方法和有限元模拟对纳米压痕实验进行分析，最终拟合出应力－应变曲线。以上力学参数的获取，保证了模拟仿真结果的准确性。

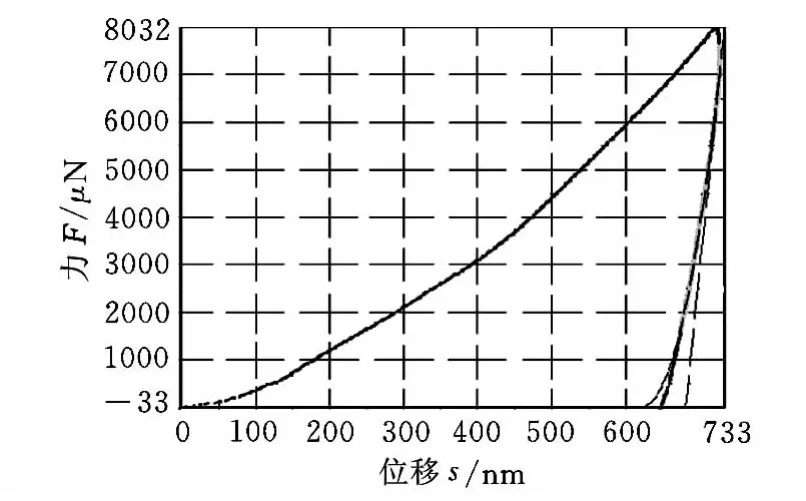
图9 铝膜纳米压痕实验图

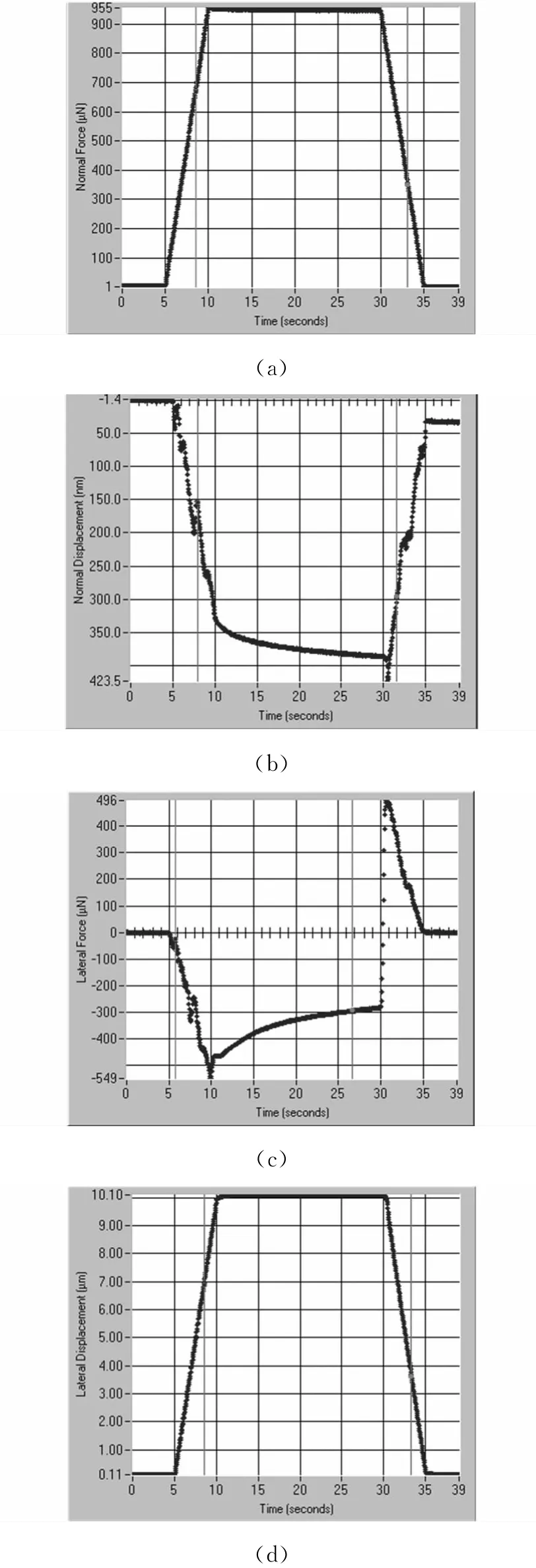
图10 纳米划痕实验图

表1 弹性模量与摩擦因数

2.2 有限元模拟分析与数据处理

通过对光栅刻划工艺的分析，采用有限元软件DEFORM［11］进行模拟时作如下设定：

（1）刻划刀为金刚石材料，其强度、硬度远高于铝膜材料，将其设为刚性材料。

（2）铝膜在刻划过程中发生塑性形变并伴有非线性弹性变形，将其设为弹塑性材料。

（3）对刻划刀作用铝膜处采用局部细化网格与自动重划网格设定，以解决运算精度与模拟时间的矛盾，使后面的正交试验具有可行性，如图11所示。

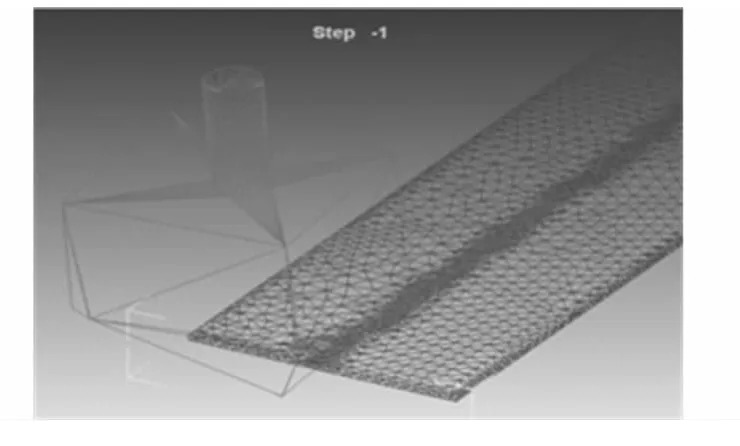
图11 局部细化网格图

模拟后为了获得准确槽形，利用DEFORM软件后处理功能对槽形作剖切分析：在光栅槽形各参数中，槽深及槽宽可通过点的坐标采集方式直接利用DEFORM 中相关功能计算得出［12］。由于DEFORM－3D不含有角度测量功能，故将槽形截面图导入CAD中进行角度测量（图12）。同时，为了提高数据采集精度，采用多次测量计算取平均值的方式。

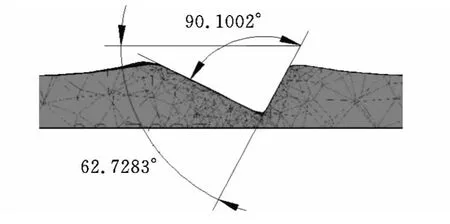
图12 光栅槽底角和闪耀角的测量

3 光栅刻划正交试验分析

为分析各工装参数对槽形的影响程度，对各影响因素取不同的水平进行正交试验。

3.1 正交试验表

正交试验［13］具有试验次数少、试验效率高、试验效果好等优点，光栅机械刻划过程中对槽形产生影响的因素有刀尖角等10个因素。水平数选的越多，规律曲线越趋于真实可信，但水平数过多，正交试验的次数越多，综合考虑正交模拟试验所需时间与可信程度，采用正交试验法并按照L50（511）进行正交试验，如表2（部分）所示。

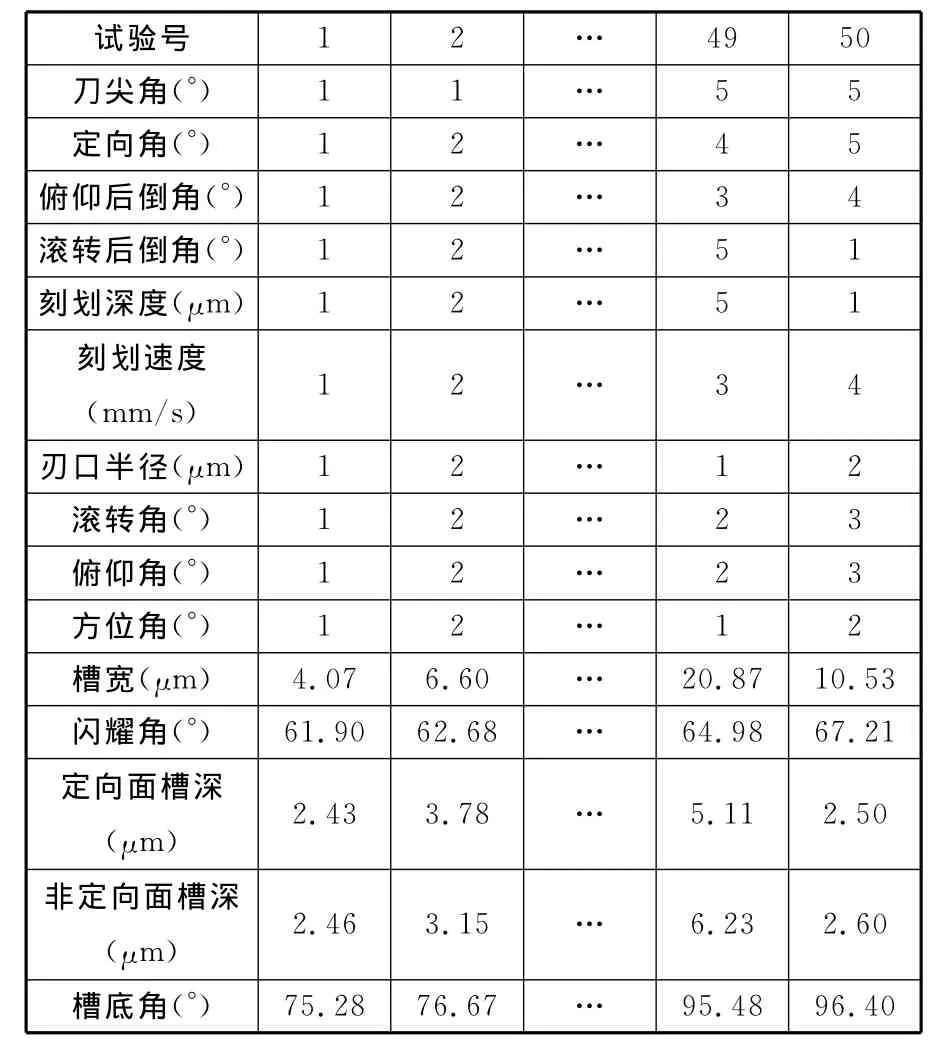
表2 正交模拟试验结果表

3.2 影响光栅槽形主次因素的分析

以槽底角为评测指标，分析各工装参数对槽底角影响轻重程度，其他槽形参数的评测与此类似。表3为10个工装参数在不同水平下，评测指标－槽底角之和列表。Ⅰ～Ⅴ分别为各影响因素的水平，R为因素的极差，即每个因素水平Ⅰ～Ⅴ中最大值与最小值之差。R越大，因素对试验指标的影响越显著。影响槽底角各因素的轻重程度从大到小排序依次为刀尖角、方位角、定向角、俯仰后倒角、刻划速度、刃口半径、刻划深度、滚转后倒角、滚转角、俯仰角。R值过小的影响因素可忽略不计，取极差为0.1，这样得到影响槽底角的主要因素：刀尖角、方位角与定向角。

表3 各因素对槽底角影响规律统计表

4 各主要影响因素对光栅槽形的影响规律分析

仍以槽底角为例，为建立一个可信的、优化的多因素数学评价模型，需要确定每个单因素对其影响规律。故采用单因素分析法，观察刀尖角、方位角与定向角对槽底角的影响关系，发现三者对槽底角的影响关系均成近似线性关系，如图13～图15所示。

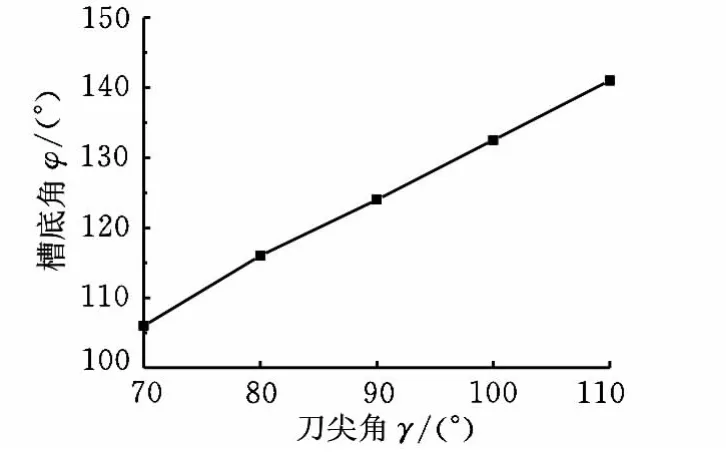
图13 刀尖角对槽底角的影响规律

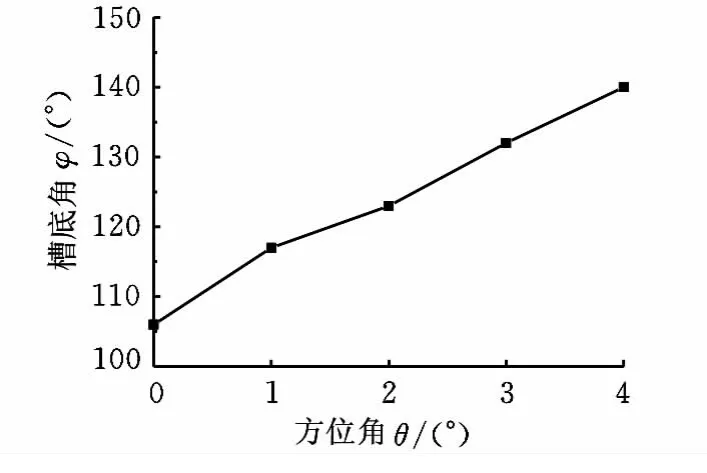
图14 方位角对槽底角的影响规律

图15 定向角对槽底角的影响规律

5 槽底角解析数学模型的建立与求解

根据主要影响因素对光栅槽形影响规律的分析，槽底角多因素解析数学模型可设为

式中，X1、X2、X3分别为刀尖角、方位角与定向角；B1、B2、B3分别为X1、X2、X3的系数。

用矩阵形式表示式（2）并变换后得系数B：

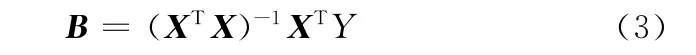
根据表3结果，对式（3）求解，得B1＝0.9763，B2＝0.9574，B3＝0.0537。故

为评测模型（式（4））整体参数的显著性，引入F检验，其中取δ＝0.001，查表F（3，46）＝6.60。而F′（3，46）＝167.4047≫F＝6.60，拒绝原假设，即自变量全体对因变量Y产生显著线性影响。

上述模型的计算与仿真是基于真实的光栅刻划过程所进行的有限元模拟分析，通过所建立的槽底角数学模型，可预先计算得到槽底角的大小。

6 光栅刻划实验［14］分析

仍以刻划79线／mm中阶梯衍射光栅90°理论槽底角为例，采用舒伯哈特公司制作的刻划刀进行刻划实验。刀具结构参数如下：刀尖角为87.5°，定向角为62.5°，后倒角为60°。安装参数如下：滚转角为2°，俯仰角为3°，方位角为0.5°，刻划深度为3.4μm。

刻划后经空间分辨达纳米级的原子力扫描电镜检测，运用NanoScope软件的section分析功能，得到实际槽形截面剖切图（图16中，角1为非闪耀角，角2为闪耀角），通过量取V1、H1、V2、H2，计算得刻划实验槽底角：

通过解式（4）得

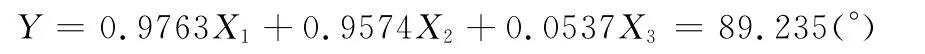
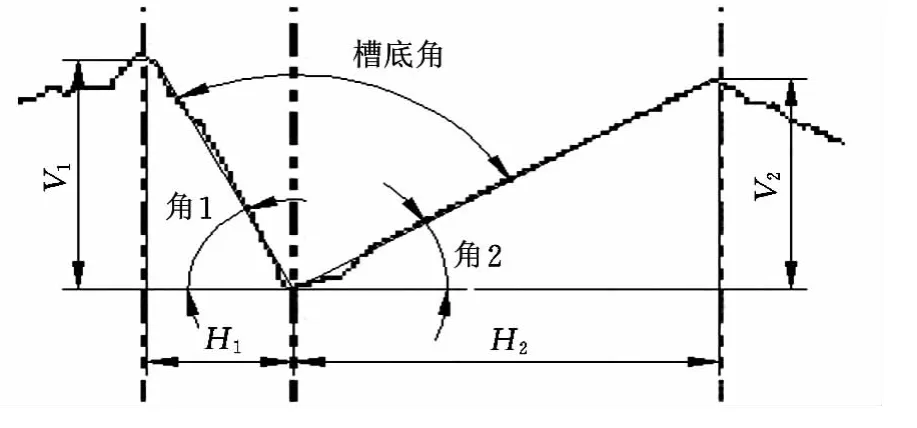
图16 实际槽形槽底角计算示意图

从观测结果可以看出，预测槽底角与实际刻划槽底角的值十分接近，证明所建立的数学模型是可用的，以刻划模拟为基础的槽形数学模型建立方法是可行的。

7 结语

采用刻划实验与有限元模拟技术相结合的研究方法，并结合正交试验与单因素试验手段，可建立以槽底角、闪耀角、槽宽、定向面槽深、非定向面槽深等为槽形评测指标的预测性解析数学模型。该项研究将有限元模拟技术、材料测试技术、实验设计与分析等多种方法相结合，成功地应用于光栅刻划工艺分析中，使刻划光栅工艺手段更先进、工艺更合理。

［1］王芳，齐向东.高精度控制光电光栅刻划机的光栅外差干涉仪［J］.激光技术，2008，32（5）：474－476.Wang Fang，Qi Xiangdong.Grating Heterodyne Interferometer of High Accuracy Controlling Photoelectric Grating Ruling Engine［J］.Laser Technology，2008，32（5）：474－476.

［2］巴音贺希格，高键翔，齐向东，等.10.6μm 激光器一级输出高衍射效率闪耀光栅的研制［J］.光电子激光，2004，15（10）：1137－1140.Bayanheshig，Gao Jianxiang，Qi Xiangdong，et al.10.6μm Development of Laser Level Output High Diffraction Efficiency of Gratings［J］.Photoelectron Laser，2004，15（10）：1137－1140.

［3］时轮，郝德阜，齐向东.高精度衍射光栅刻划机的最新技术进展［J］.仪器仪表学报，2001，22（4）：438－439.Shi Lun，Hao Defu，Qi Xiangdong.The Latest Progress in Technology of High Precision Diffraction Grating Ruling Engine［J］.Chinese Journal of Scientific Instrument，2001，22（4）：438－439.

［4］李英海，巴音贺希格，齐向东.用于衍射光栅刻划的超精密金刚石刻刀的研制［J］.微细加工技术，2006，12（6）：15－17.Li Yinghai，Bayanheshig，Qi Xiangdong.Development of Ultra Precision Diamond Graver for Diffraction Grating［J］.Micro Machining Technology，2006，12（6）：15－17.

［5］李英海.超精密金刚石刀具－衍射光栅刻划刀［J］.光学精密工程，1996，4（3）：81－84.Li Yinghai.Ultra Precision Diamond Cutting Tool－diffraction Grating Knife［J］.Optics and Precision Engineering，1996，4（3）：81－84.

［6］沈彬，孙方宏，薛宏国，等.高性能复杂形状金刚石薄膜涂层刀具的制备和切削性能研究［J］.中国机械工程，2008，19（19）：2287－2291.Shen Bin，Sun Fanghong，Xue Hongguo，et al.High Performance Complex Shape of Diamond Film Coated Tools Preparation and Study on the Cutting Performance［J］.China Mechanical Engineering，2008，19（19）：2287－2291.

［7］马德军，徐可为，何家文.利用纳米压人加载曲线确定金属薄膜的屈服强度和硬化指数.ⅠⅡ 实验及验证［J］.金属学报，1999，35（10）：1049－1052.Ma Dejun，Xun Kewei，He Jiawen.Using Nano Indentation Loading Curve to Determine the Yield Strength and Hardening Exponent of Thin Metal Films.ⅠⅡTest and Verification［J］.The Journal of Metallography，1999，35（10）：1049－1052.

［8］马德军，刘建敏.材料杨氏模量的纳米压入识别［J］.中国科学E辑：工程科学和材料科学，2004，34（5）：493－509.Ma Dejun，Liu Jianmin.Young’s Modulus of Nano Indentation Recognition［J］.Science in China Series E：Engineering Science and Materials Science，2004，34（5）：493－509.

［9］Dao M，Chollacoop N，Van Vliet K J，et al.Computational Modeling of the Forward and Reverse Problems in Instrumented Sharp Indentation［J］.Acta Mater，2001，49（19）：3899－3918.

［10］Oliver W C，Pharr G M.An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments［J］.J.Mater.Res.，1992，7（6）：1564－1583.

［11］胡建军，李小平.DEFORM－3D塑性成形CAE应用教程［M］.北京：北京大学出版社，2011.

［12］张莉，李升军.DEFORM在金属塑性成形中的应用［M］.北京：机械工业出版社，2009.

［13］栾军.现代试验设计优化方法［M］.上海：上海交通大学出版社，1995.

［14］张宝庆，史国权，石广丰，等.衍射光栅机械刻划成槽的预控试验［J］.光学精密工程，2013，21（7）：1666－1675.Zhang Baoqing，Shi Guoquan，Shi Guangfeng，et al.Pre－control of Mechanical Scratching Diffractive Grating［J］.Optics and Precision Engineering，2013，21（7）：1666－1675.