65m射电望远镜副面调整机构容错策略与工作空间边界识别

窦玉超 姚建涛 侯雨雷 赵永生

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004

2.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

0 引言

为实现65m射电望远镜波段转换和副面指向误差修正，在副面与桁架之间加装了Stewart型并联调整机构。该机构具有一定的运动容错能力，可提高射电望远镜的可靠性。

关于机器人的运动容错方法，Monteverde等［1］提出了在并联机器人驱动分支上安装冗余电机或冗余驱动分支的方法进行容错。Yi等［2］将并联机构失效形式分为位置失效、转矩失效、硬件失效，分析了3种失效对机构运动学的影响，采用工作空间冗余和运动学冗余的方法实现了机构容错。Notash等［3］将并联机构的失效形式分为运动失效、驱动失效、传感器失效，分别给出了相应的容错策略。Li等［4］对串联机器人的冗余驱动关节在容错运动过程中的轨迹规划问题进行了研究。Hassan等［5］在各分支上添加冗余驱动关节，实现了并联机器人的运动容错。通过冗余驱动或冗余自由度实现串联机器人容错的研究较多，但将冗余自由度用于并联机器人容错研究并进行应用的报道较少。使用该容错方法得到的工作空间受故障分支长度约束，将小于其正常工作空间，因此精确的工作空间计算方法和边界识别策略是提高容错效果的重要手段。徐刚等［6］采用并联机构在36个特定方向上运动范围的交集对不同机构工作空间的大小进行评价，忽略了姿态和运动副干涉对工作空间的影响。李保坤等［7］将并联机器人非奇异工作空间的内切球作为其实际工作空间，缩小了机器人实际工作范围。Wang等［8］采用统一算法对并联机器人的可达工作空间和灵活工作空间的计算方法进行了研究。荣誉等［9］研究了六足机器人的（U＋UPR）P＋UPS型腿部结构参数对其工作空间性能的影响。袁立鹏等［10］建立了并联机器人机构尺寸参数与工作空间的数学关系。刘欣等［11］进行了欠约束、完全约束、冗余约束3种情况下的一致工作空间存在的证明并得到了求解策略。上述文献研究了结构参数对工作空间大小的影响，却忽视了不规则工作空间边界识别方法对机构实际工作范围的影响。

针对如何实现并联机构运动容错和工作空间边界识别的问题，首先分析了单分支驱动故障对机构自由度的影响，提出利用冗余自由度进行容错的原理，对比了在L波段和S波段指向发生故障时机构可实现的极限工作空间，提出了工作空间不规则边界的识别方法，实现了不规则工作空间边界对机构运动范围的约束。

1 副面并联调整机构容错原理

1.1 并联调整机构自由度分析

副面的Stewart型并联调整机构结构如图1所示。该并联调整机构由固定平台、运动平台及连接固定平台和运动平台的6个驱动分支组成。每个分支由胡克铰（U副）、移动副（P副）及球铰（S副）依次连接而成。其中，胡克铰Bi与固定平台相连，球铰bi与运动平台相连，移动副为驱动副。分别在固定平台和动平台平面内中心点建立直角坐标系oxyz、o1x1y1z1，y轴与 ∠B1oB2的角平分线重合，y1轴与 ∠b1ob2的角平分线重合，z轴、z1轴分别垂直于固定平台、动平台平面竖直向上，坐标系o1x1y1z1相对坐标系oxyz的位姿即为动平台位姿。

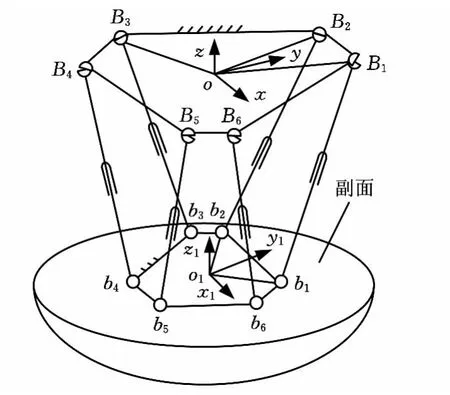
图1 并联调整机构简图

当分支Bibi驱动发生故障导致驱动副P锁死成为定长杆时，故障分支可等效为US结构，而其他分支均具有6个自由度，所以动平台的自由度取决于故障分支的自由度。为分析故障分支的自由度，建立该分支的运动螺旋系，如图2所示。

任意位姿下故障分支的运动螺旋系为

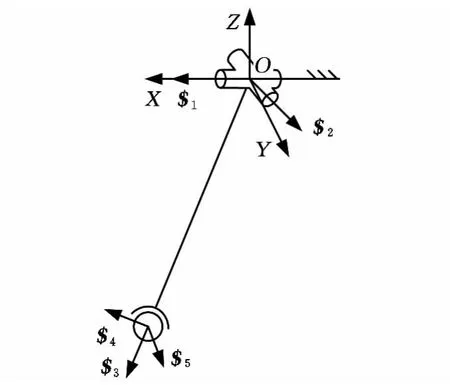
图2 故障分支运动螺旋系

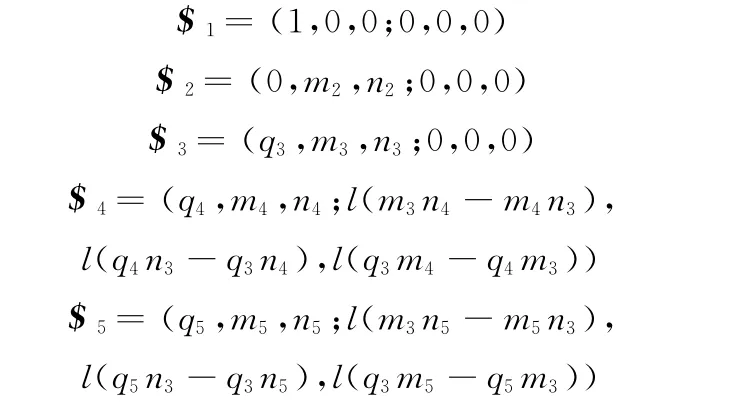
式中，l为发生故障时的分支长度；qs、ms、ns分别为运动副s轴线单位矢量的分量，s＝1，2，…，5。

由故障分支的运动螺旋系可得其反螺旋：

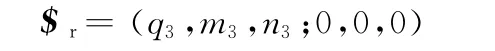
＄r表示一个沿（q3，m3，n3）方向的约束力螺旋。该约束力螺旋轴线与分支杆轴线重合，由此表明该故障分支约束了动平台沿杆长方向的瞬时移动自由度。

1.2 基于冗余自由度的容错原理

假设分支Bibi发生故障时杆长为l，动平台期望位姿为动坐标系o1x1y1z1相对固定坐标系oxyz的位姿：

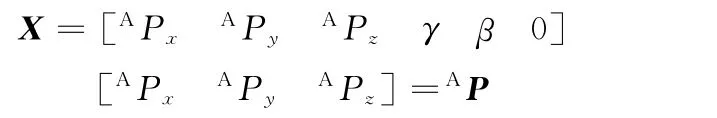
式中，AP、［γ β 0］分别为坐标系o1x1y1z1相对坐标系oxyz的位置和姿态。

以X－Y－Z欧拉角表示坐标系o1x1y1z1相对坐标系oxyz的旋转变换，变换矩阵为

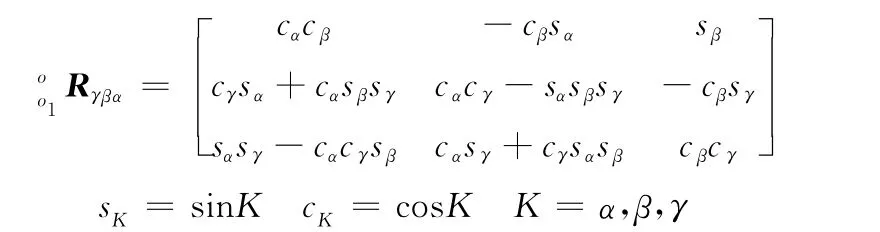
则球铰bi（i＝1，2，…，6）在坐标系oxyz下的位置矢量可表示为

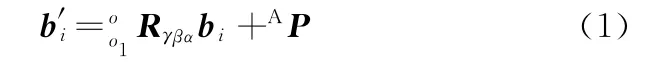
式中，bi为第i个球铰在坐标系o1x1y1z1下的位置。

可求得分支Bibi运动学反解：

式中，Bi为第i个胡克铰在坐标系oxyz下的位置。

显然，当li≠l时，动平台无法到达期望位姿。但因动平台绕其轴线z1的转动并不影响副面指向，故可将动平台绕z1轴转动α，如图3所示。

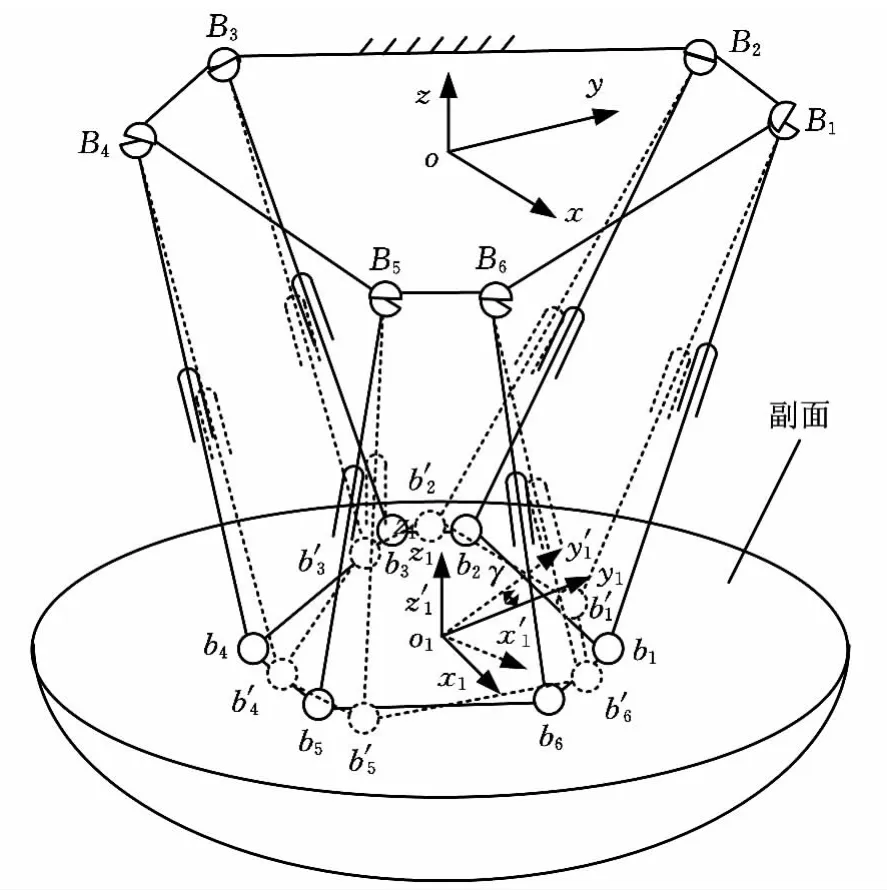
图3 并联调整机构容错原理图

调整后动平台位姿为动坐标系o′1x′1y′1z′1在固定坐标系oxyz下所表示的位姿：

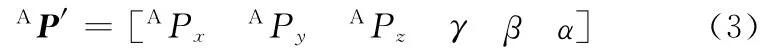
将式（3）所表示的位姿代入式（2），可求得调整后分支Bibi运动学反解：

式中，b″i为坐标系o′1x′1y′1z′1所示位姿下球铰在坐标系oxyz下的位置。

令l′i＝l，可求得转角α与期望位姿以及杆长l的函数关系：

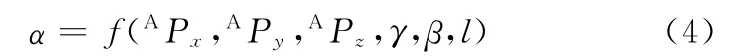
将式（3）所表示的位姿、式（4）代入式（2），可求得并联机构在位姿AP′下的运动学反解：

基于冗余自由度的并联调整机构容错原理可总结为：根据动平台期望位置AP和故障分支杆长l，将动平台绕z1轴转动α，使得调整后的动平台位姿AP′所对应的故障分支运动学反解与分支发生故障时的杆长相等，并按照调整后动平台位姿分别计算其他分支的运动学反解。因动平台绕z1轴转动并不影响副面指向，故可利用式（5）进行并联机构的运动学反解计算，为实现并联调整机构的容错运动提供理论支撑。

2 容错情况下工作空间分析与边界识别

2.1 容错情况下工作空间对比分析

容错情况下，并联调整机构所能实现的工作空间是否满足副面指向调整的需要，决定着能否将上述容错原理应用于实际工作，因此需要进行并联调整机构容错情况下的工作空间计算。

首先根据射电望远镜的方向图对副面位姿进行校正，从而获得射电望远镜主反射面基准俯仰角（50°）及极限俯仰角（5°和90°），射电望远镜在S波段和L波段副面的位姿如表1所示。

表1 副面位姿调整范围

由表1可以看出，射电望远镜工作在S波段和L波段时，主反射面俯仰角从5°至90°调整过程中，副面位置调整范围均为：5.140mm≤x≤5.956mm，0.751mm≤y≤62.110mm，11.410mm≤z≤31.607mm。但副面姿态调整范围并不一致，S波段：0.018 68°≤γ≤0.146 35°，－0.072 91°≤β≤－0.071 36°。L波段：3.968 68°≤γ≤4.096 35°，－0.072 91°≤β≤－0.071 36°（姿态是多个角度的耦合，就单个角度而言确实没有变化，但对于姿态来说是不相同的）。由于副面具有轴对称性，故绕副面轴线转动的α角没有发生变化。以上的副面位姿调整范围即为保证射电望远镜正常工作所需并联调整机构工作空间。

为了计算容错情况下并联调整机构的工作空间，以初始位姿下动坐标系原点为中心，划定涵盖工作空间的立方体区域，将其离散成有限个小立方体的集合。以小立方体的顶点作为目标点，以（i，j，k）（i，j，k＝1，2，…，n）表示目标点在工作空间中的位置序列。在每个目标点处对并联调整机构姿态逐一进行赋值，采用上一节提出的容错原理进行运动学反解计算，并将分支杆是否超出行程，胡克铰、球铰和分支杆间是否发生干涉作为判断目标点是否在工作空间内的依据。所有可到达的小立方体顶点覆盖的空间区域即为并联调整机构在容错情况下的工作空间。该工作空间的搜索流程如图4所示。

使用上述工作空间计算方法对射电望远镜工作在S波段和L波段并联调整机构故障后的极限工作空间进行计算。工作在S波段时，最小、最大工作空间分别发生在2号分支长度为2346.267mm和3号分支长度为2417.517mm时。工作在L波段时，最小、最大工作空间分别发生在6号分支长度为2318.640mm和4号分支长度为2487.044mm时，将调整机构故障后工作空间与其正常工作空间进行对比，如图5所示。可见故障情况下使用容错原理获得的工作空间明显小于正常工作空间，且均发生部分边界超出正常工作空间的现象。这是由于故障情况下动平台为到达期望位姿绕自身轴线进行转动调整，使得并联机构在该方向上运动范围增大。

图4 容错工作空间计算

如图6所示，将射电望远镜工作在S波段和L波段时并联机构发生单分支驱动故障后可实现的最小工作空间与保障射电望远镜正常工作时副面的调整范围进行对比分析。从图6可以看出，L波段和S波段故障情况下的最小工作空间存在交集，且该交集完全涵盖了保障射电望远镜正常工作副面所需的调整范围，即机构在任意位姿下发生故障后，采用容错方法所实现的工作空间均能满足副面指向调整的需要。

2.2 工作空间边界识别

为实现对工作空间边界的识别，在利用前述工作空间计算方法获得的工作空间基础上，计算目标点p与工作空间中所有小立方体顶点（xi，yi，zi）的距离，通过判断与点p 距离最近的小立方体顶点pijk是否位于工作空间内，实现对点p是否位于工作空间内的判断。点p、点pijk、工作空间之间的相对位置关系如图7所示。

图5 故障情况下工作空间与正常工作空间对比

图6 最小工作空间与副面调整范围

图7a中，最近点pijk为工作空间范围内相邻8个小立方体的公共顶点，因点p与pijk之间的距离小于小立方体的体对角线长度的一半，因此点p必位于某个小立方体的内部，即位于工作空间范围内。图7b～图7d给出了其他3种目标点p、最近点pijk、工作空间的相对位置关系，在这3种情况下，点p可能在工作空间内与点pijk最近，也可能在工作空间外与点pijk最近，分别在p0和p′0所示位置。对应此类情况，安全起见，认为点p位于工作空间范围外。即只有最近点pijk为8个相邻小立方体的公共顶点时，才视目标点p位于工作空间范围内。

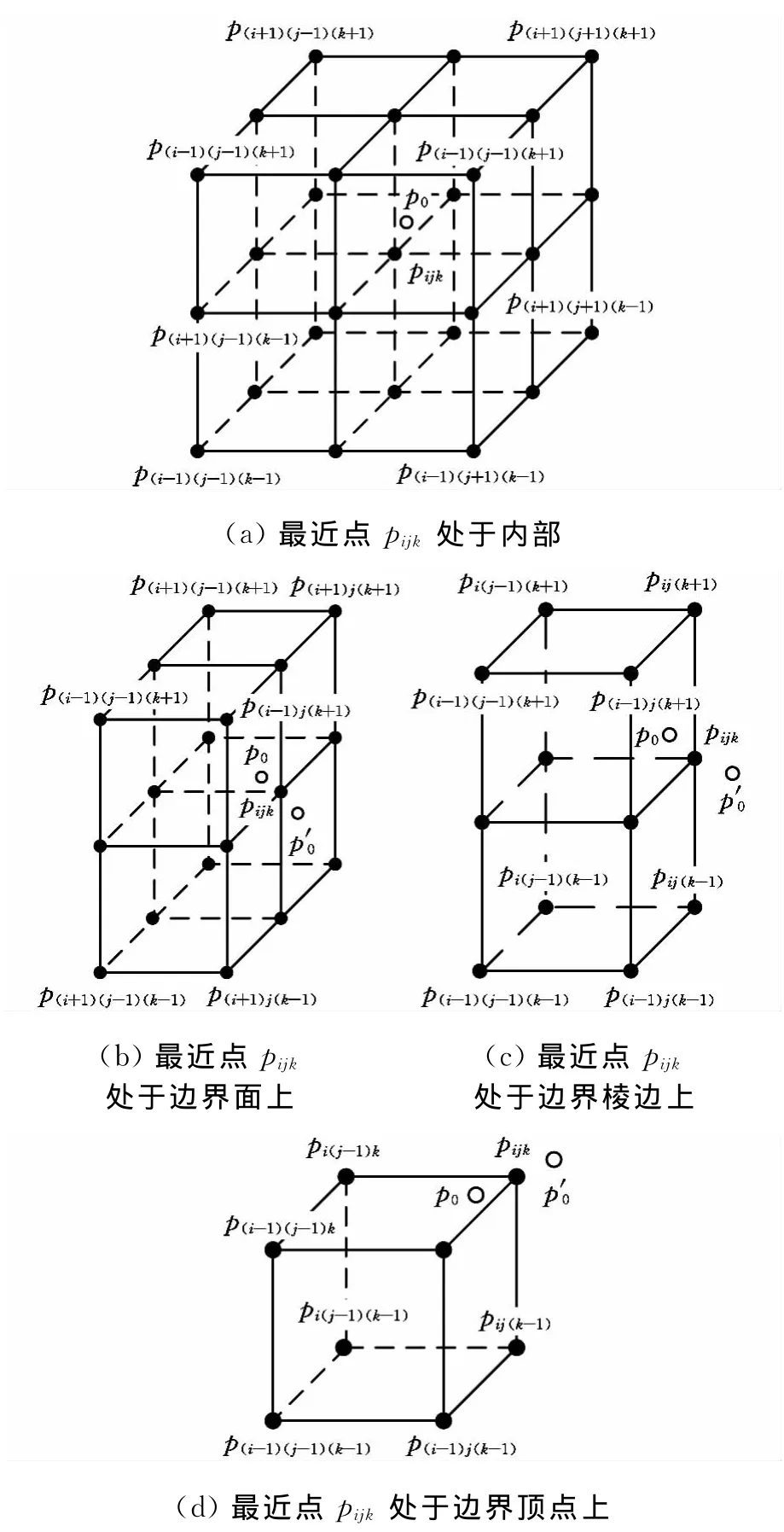
图7 目标点与工作空间边界关系

使用上述方法对工作空间边界进行识别，其精确程度取决于在进行工作空间计算时离散的小立方体棱长，该值越小，对工作空间边界的识别精度越高。

3 并联调整机构容错运动实验

65m射电望远镜已于2012年10月落成并投入使用，其副面并联调整机构如图8所示。为验证本文所提出的容错原理的有效性，进行了现场实验。

实验模拟机构在2号分支长度为2346.267mm时发生故障，要求射电望远镜俯仰角从5°调整至90°，副面位姿从

调整到

以实现馈源由S波段到L波段的切换。

副面从位姿A调整到位姿B的过程中采用直线轨迹进行过渡，使用本文提出的单分支驱动故障容错原理对并联机构的运动学进行计算，实现副面位姿的调整。

由于并联调整机构安装在近70m的高空，现有测量设备难以实现对如此远距离目标的精确测量。为了验证副面是否按照预定运动轨迹到达指定位姿，在并联调整机构运动过程中采集各驱动分支杆长传感器磁尺反馈的数据，如图9所示。采用运动学正解对调整机构运动过程中副面的位置和姿态进行计算，计算结果分别如图10、图11所示。

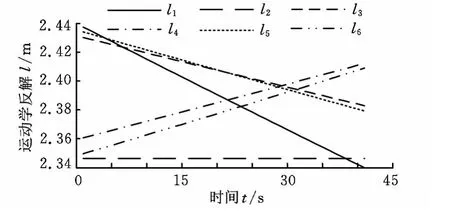
图9 并联调整机构运动学反解

从图10、图11所示的副面位姿调整过程可以看出，副面并未按照设计的起止位姿进行调整，而是从位姿

调整到

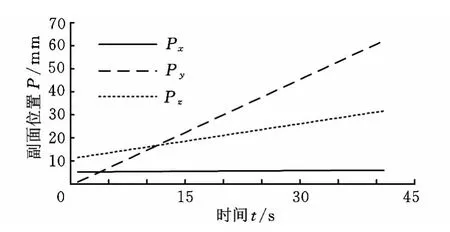
图10 副面位置调整过程

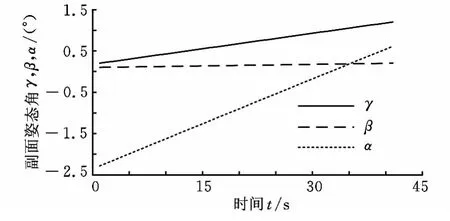
图11 副面姿态调整过程

副面绕与自身轴线重合的z1轴从－2.284 00°转动至0.612 10°，其他5个自由度方向的调整与预期设计的调整过程一致。由于副面绕与自身轴线重合的z1轴转动，副面指向并不发生改变，所以并联调整机构按照预定轨迹实现了对副面位姿的调整。

4 结语

本文以确保上海65m射电望远镜副面并联调整机构正常运行为目的，分析了调整机构单分支驱动故障对机构自由度的影响，提出了利用冗余自由度实现容错运动的方法，并对故障后可实现的容错运动范围进行了计算分析；实现了对机构不规则工作空间边界的识别，避免了设备超出工作空间造成的损坏；实验证明了所提出容错原理的有效性，成功实现副面位姿的调整，提高了射电望远镜运行的可靠性。

［1］Monteverde V，Tosunoglu S.Development and Application of a Fault Tolerance Measure for Serial and Parallel Robotic Structures［J］.International Journal of Modelling ＆Simulation，1999，19（1）：45－51.

［2］Yi Yong，McInroy J E，Chen Yixin.Fault Tolerance of Parallel Manipulators Using Task Space and Kinematic Redundancy［J］.IEEE Transactions on Robotics，2006，22（5）：1017－1021.

［3］Notash L，Huang Li.On the Design of Fault Tolerant Parallel Manipulators［J］.Mechanism and Machine Theory，2003，38：85－101.

［4］Li Kene，Zhang Yunong.Fault－tolerant Motion Planning and Control of Redundant Manipulator［J］.Control Engineering Practice，2012，20：282－292.

［5］Hassan M，Notash L.Optimizing Fault Tolerance to Joint Jam in the Design of Parallel Robot Manipulators［J］.Mechanism and Machine Theory，2007，42：1401－1417.

［6］徐刚，杨世模.Gough－Stewart平台机构的普适工作空间及其几何求解［J］.光学精密工程，2008，16（2）：257－264.Xu Gang，Yang Shimo.Universal Workspace Characteristics of Gough－Stewart Platform and Its Analytic Solution［J］.Optics and Precision Engineering，2008，16（2）：257－264.

［7］李保坤，曹毅，黄真，等.基于单位四元数的Stewart机构姿态工作空间研究［J］.机器人，2008，30（4）：353－358.Li Baokun，Cao Yi，Huang Zhen，et al.Orientation Workspace Analysis of Stewart Platform Based on Unit Quaternion［J］.Robot，2008，30（4）：353－358.

［8］Wang Zhongfei，Ji Shiming，Li Yanbiao，et al.A Unified Algorithm to Determine the Reachable and Dexterous Workspace of Parallel Manipulators［J］.Robotics and Computer－Integrated Manufacturing，2010，26：454－460.

［9］荣誉，金振林，曲梦可.六足步行机器人的并联机械腿设计［J］.光学精密工程，2012，20（7）：1532－1541.Rong Yu，Jin Zhenlin，Qu Mengke.Design of Parallel Mechanical Leg of Six－legged Robot［J］.Optics and Precision Engineering，2012，20（7）：1532－1541.

［10］袁立鹏，赵克定，许宏光.Stewart平台铰点工作空间的研究［J］.航空学报，2006，27（5）：979－984.Yuan Lipeng，Zhao Dingke，Xu Hongguang.Study on Vertex Space of Stewart Platform［J］.Acta Aeronauticaet Asronautica Sinica，2006，27（5）：979－984.

［11］刘欣，仇原鹰，盛英.绳牵引并联机器人工作空间的存在条件证明及一致求解策略［J］.机械工程学报，2010，46（7）：27－34.Liu Xin，Qiu Yuanying，Sheng Ying.Proofs of Existence Conditions for Workspaces of Wire－driven Parallel Robots and a Uniform Solution Strategy for the Workspaces［J］.Chinese Journal of Mechanical Engineering，2010，46（7）：27－34.