混合不确定条件下基于信息公理的产品服务系统方案评价

陈东萍，褚学宁，冯 涛，李玉鹏，左冠丽

（上海交通大学 机械与动力工程学院，上海 200240）

0 引言

作为公理设计（Axiomatic Design，AD）最重要的两个公理之一，信息公理为方案评价提供了一种新的手段［1］。应用信息公理进行方案评价，需要确定评价指标的设计范围和系统范围，以计算各指标的信息量（即系统范围满足设计范围的成功概率的对数负值），并依据信息量的大小确定最佳方案，而不需要决策者给出评价指标的权重，避免了人为主观因素的影响。因此，信息公理在产品、服务和制造系统等领域的方案评价中得到了广泛应用［2-3］。

在基于信息公理的方案评价过程中，评价指标的系统范围有可能是确定性或随机性的变量，需要分别构建不同的信息量计算模型［4］。对于确定性系统范围变量，已有一些文献引入了模糊集合理论［5-6］，定义了模糊系统范围、设计范围和公共范围，构建了模糊评价指标信息量的计算模型。这一模型能够较好地解决定性指标的信息量计算问题，拓展传统信息公理评价方法的应用范围。

然而，对于系统范围为随机变量的情况，目前尚未有文献开展模糊性评价研究。在工程实际中，有很多系统范围为随机变量的定性指标，也需要用模糊语言来刻画决策者的定性评价。例如，服务方案评价中的及时性指标，其系统范围的随机性来源于服务的异质性［7-8］（因每次服务的地点、请求时间和传送方式等不同而有偏差，这时及时性指标表现为满足一定概率分布的随机变量）。此外，对于及时性指标的评价值，决策者往往习惯采用“很快”、“快”、“一般”、“慢”、“很慢”等定性语言来表达［9-11］。针对这类系统范围为随机变量的指标，在考虑评价值为模糊概念的条件下，其信息量的计算涉及上下界为模糊数的积分，现有的模糊信息公理无法直接计算。因此，需要提出随机性和模糊性共存的混合不确定条件下的信息公理评价方法。

混合不确定条件下，信息公理的评价方法存在如下难点：传统信息公理的指标仅能单独表达其随机性或模糊性，如何对混合不确定评价指标进行建模，使同一个指标同时反映随机性和模糊性，是本文要解决的第一个问题；由于混合不确定指标的成功概率是上下界为模糊数的积分，无法直接计算其信息量，如何计算混合不确定指标的信息量，是本文要解决的第二个问题。针对上述难点，本文提出在混合不确定条件下基于信息公理的方案评价方法，并基于模糊模拟方法提出混合不确定评价指标的信息量计算方法。

1 混合不确定条件下的评价指标建模

1.1 传统、模糊和混合不确定三种信息公理对比

模糊性和随机性是现实系统中普遍存在的两种不确定性［12］。随机性是描述事件是否发生的不确定性，而模糊性是描述决策者对概念认知的不确定性。在应用信息公理进行评价时，需确定每一个指标的设计范围和系统范围。设计范围是决策者期望指标达到的范围，分为定量和定性两种变量，其中定性的设计范围变量适合应用模糊数学理论研究；系统范围是方案执行后指标的实际可达范围，分为确定和随机两种变量，其中随机性来源于每次实际执行过程的偏差，适合用概率与统计理论研究。例如服务方案评价中的服务速度、服务成本等指标，其设计范围是模糊变量，系统范围是随机变量。因此，本文提出以随机变量表达系统范围、以模糊变量表达设计范围的混合不确定指标模型，开展模糊性、随机性共存的方案评价。表1从信息量计算公式、适用范围、研究现状等方面对比了信息公理、模糊信息公理和本文所提混合不确定下的信息公理。

表1 三种信息公理的对比

为推导混合不确定条件下信息量的计算方法，下面给出随机变量和模糊变量的定义。

定义1［17］设ξ是从可能性空间｛θ，p（θ），Pos｝到实数集R的一个函数，则称ξ为一个模糊变量。

定义2［17］设ξ是可能性空间｛θ，p（θ），Pos｝的模糊变量，则称

是ξ的α-水平截集。

定义3［17］设ξ是可能性空间｛θ，p（θ），Pos｝的模糊变量，则由可能性测度导出函数

称为ξ隶属度函数。

定义4［17］一个随机变量就是从概率空间（Ω，A，Pr）到实数集的可测函数。

1.2 评价指标分类及混合不确定指标信息量定义

依据表1，在应用信息公理进行方案评价时，需要根据指标的不确定性选择不同模型计算指标的信息量。因此本文依据指标的模糊性和随机性，提出以下四类评价指标：确定性指标、模糊指标、随机指标和混合不确定指标（如图1）。其中：确定性指标和随机指标的信息量可按照传统信息公理计算，模糊指标的信息量按照模糊信息公理计算，混合不确定指标信息量的计算方法是随机指标计算方法的扩展。

随机指标信息量

式中：p为满足给定功能需求FR的成功概率，f（FR）为功能需求FR的系统范围的概率密度函数，drl和dru是设计范围的上界和下界。对于混合不确定指标，其设计范围是模糊变量，成功概率p的积分上下限是模糊数，难以依据式（3）直接计算。为此，本文定义了混合确定指标信息量计算公式。

定义5 混合不确定指标信息量计算公式为

以服务方案评价指标及时性为例，说明混合不确定指标的建模过程。及时性的设计范围是模糊集｛很快，快，一般｝，评价术语集如图2c所示，其系统范围是一个随机变量，分布服从特定的概率密度函数（Probability Density Function，PDF），如图2b所示。图2a展示了混合不确定指标及时性的设计范围和系统范围。根据信息量的计算公式，混合不确定指标信息量

式中：p为满足及时性的成功概率，f（FR）为及时性系统范围的概率密度函数；M和VF为设计范围的上下界，分别表示“中等”和“很快”。

2 混合不确定指标信息量算法

为计算混合不确定条件下的指标信息量，采用模糊模拟方法，将上下限为模糊数的积分转换为一系列精确数积分的加权和。评价指标主要有成本型、效益型和固定型等，成本型和效益型指标的成功概率积分上下界中仅有一个是模糊数，固定型指标的成功概率积分上下界都是模糊数，其计算过程略有不同。

2.1 基于模糊模拟的信息量计算方法

模糊模拟由文献［18-19］提出，它是对模糊系统模型进行抽样实验的一项技术，在处理包含模糊参数的不确定函数方面很有优势［17］。模糊模拟处理不确定函数的主要思想是在模糊数的α-水平截集中取一系列离散的点代表连续变化的模糊数，分别计算这些离散点的函数值，通过一定的方式将离散点的函数值合成，即得到不确定函数的值。因此如何合成离散点处的函数值是模糊模拟的关键。本文借鉴模糊变量期望的模拟方法，对离散点处的函数值进行加权和运算，获取成功概率p。由定义3可知，隶属函数是可能性的度量，本文根据各离散点的隶属度对其函数值赋权，把各离散点的隶属度做归一化处理，设置为各离散点的权重，具体流程如图3所示。

下面通过一个简例说明本算法思路。如图2所示，混合不确定指标及时性的系统范围是概率密度函数为f（x）的随机变量（如图2b），设计范围是“很快”、“快”或“一般”。根据式（3），指标的成功概率p是上界为模糊数的积分，其中dru是“一般”，其α-水平截集为（0，48）h，α=0。为采用模糊模拟的方法计算p值，在α-水平截集中取一系列离散点，为方便说明，此例中仅取x1，x2和x3三个点，如图2c所示，对应的隶属度分别为μ（x1），μ（x2）和μ（x3），成功概率分别为。此三点处函数值（成功概率p1，p2，p3）的权重为隶属度的归一化值，。指标的成功概率p为各离散点处函数值的加权和。因此“服务及时性”这一指标的信息量为I=

混合不确定条件下，成本型和效益型指标公共范围的上下界中只有一个是模糊变量，固定型指标公共范围的上下界都是模糊变量，如图4所示。以成本型指标为例，说明混合不确定指标公共范围的特点。如图4a所示，由于公共范围的上界是模糊变量，图中斜线所示区域为公共范围的模糊边界，这部分公共范围的计算难以采用传统的信息量计算公式。同理，效益型指标和固定型指标的信息量计算方法也需重新设计。

2.2 成本型和效益型混合不确定指标信息量算法流程

步骤1 确定系统范围的概率分布函数f（x）。

步骤3 在区间［a，c］中取一系列均匀分布的离散点xi，其中i=1，2，…，M，M为一个足够大的数（一般M≥100）。

步骤4 计算各离散点xi的隶属度μ（xi）及此处函数值的权重wi，

步骤5 计算各离散点处的成功概率

步骤6 计算此指标成功概率p和信息量I：

2.3 固定型混合不确定指标信息量算法流程

步骤1 确定随机变量的概率分布函数f（x）。

步骤3 分别在区间［a1，c1］，［a2，c2］中随机取一系列离散点，其中i=1，2，…，M，j=1，2，…，M，并使，得到M组区间

步骤5 计算随机变量成功的概率，以M个区间的加权概率之和的形式表示为

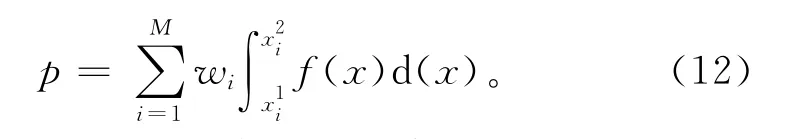
步骤6 计算随机变量的信息量

3 实例

3.1 混合不确定条件下基于信息公理的评价

某著名工程机械企业在新型号起重机产品服务系统方案的研发过程中，确定了5个可行的方案a1，a2，a3，a4，a5。针对这些方案，用所提方法进行评价优选。

步骤1 确定起重机产品服务系统的评价指标，即概念方案设计阶段定义的功能需求（如表2）。其中维修效率、维修成本、维修及时性是混合不确定指标。

步骤2 确定评价指标的设计范围和系统范围。设计范围由决策者根据用户的需求确定（如表2），设计范围的评价术语集和隶属度函数如图5所示，其中图5c的横坐标是维修的费用与产品成本的百分比。

系统范围一般由专家根据经验、知识和历史数据等进行统计分析获得。在多数情况下，对数正态分布是应予使用的最佳分布［20］。因此本案例采用对数正态分布描述c6，c7，c8，其值的对数值满足正态分布N（u，σ）。也可以根据历史数据或专家经验选择其他分布。表3列出了各方案中每个指标的系统范围。

表2 评价指标及其设计范围

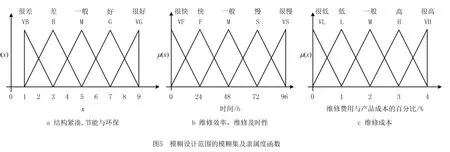
表3 各方案中每个指标的系统范围

步骤3 计算每个方案ak的每个指标的信息量

根据传统信息公理计算c1，c2和c3的信息量，根据模糊信息公理（如表1）计算c4和c5的信息量，根据2.3节提出的混合不确定指标算法，计算c6，c7和c8的信息量，结果分别如表4～表6所示。

表4 c1，c2和c3的信息量

续表4

表5 c4和c5的信息量

续表5

步骤4 计算每个方案ak的信息量，将所有指标的信息量相加得到该方案的信息量，结果如表7所示。

表6 c6，c7和c8的信息量

表7 各方案信息量

按信息量从小到大排序（如表7），a5＞a1＞a3＞a4＞a2，方案a5的信息量最小，是最佳的起重机产品服务系统方案。

3.2 基于传统信息公理的评价

为了验证所提方法的有效性和优越性，现将该方法与传统的信息公理设计方法进行比较。c1～c5的信息量计算方法与3.1节相同。其中c1，c2和c3按照传统的信息公理计算，c4和c5按照模糊信息公理计算。传统的信息公理不考虑随机性指标的模糊性，因此c6，c7，c8的设计范围是精确区间，分别为［0，51.5］h，［0，1.5］%和［0，34.0］h。其信息量的计算结果如表8所示，各方案的信息量及排序如表9所示。

表8 传统的信息公理中c6，c7，c8的信息量

表9 传统的信息公理中各方案的信息量

由表9可知，传统信息公理的排序a5＞a3＞a1＞a4＞a2与本文所提方法的排序结果略有不同（a3与a1的次序不同）。由于所提方法对系统范围为随机变量的评价指标，采用模糊数描述其设计范围，能更有效地表达实际评价过程中决策者的意图。而传统的信息公理将这些指标的设计范围表示成定量的数值，没有考虑评价值的模糊性，造成某些信息丢失，使计算结果不够准确。因此，本文提出的方法更有效、实用。

4 结束语

本文针对方案评价中存在模糊和随机两种不确定因素的特点，提出混合不确定条件下基于信息公理的方案评价方法，构建了以随机和模糊变量分别表达系统和设计范围的混合不确定性指标模型，针对成本型、效益型和固定型指标，采用模糊模拟方法分别提出信息量的计算方法。以起重机产品服务系统方案评价为例，验证了所提方法的可行性和有效性。本文的主要贡献在于：

（1）拓展了信息公理的应用范围，提出以随机变量表示系统范围、以模糊变量表示设计范围的混合不确定性处理方法，对同时具有模糊性和随机性因素的方案评价具有重要的参考价值。

（2）提出了混合不确定条件下评价指标信息量的计算方法，分别针对成本型、效益型和固定型指标，采用模糊模拟方法提出其信息量的算法，将上界和下界为模糊数的积分转化为离散点积分的加权和，通过信息量比较获得最佳方案。

［1］XIAO Renbin，CHENG Xianfu，LIAO Xiaoping.Evaluation method and its application for design scheme based on fuzzy information axiom［J］.Computer Integrated Manufacturing Systems，2007，13（12）：2331-2338（in Chinese）.［肖人彬，程贤福，廖小平.基于模糊信息公理的设计方案评价方法及应用［J］.计算机集成制造系统，2007，13（12）：2331-2338.］

［2］BABIC B.Axiomatic design of flexible manufacturing systems［J］.International Journal of Production Research，1999，37（5）：1159-1173.

［4］SUH N P.Axiomatic design：advances and applications［M］.New York，N.Y.，USA：Oxford University Press，2001.

［5］OSMAN K，CENGIZ K.Fuzzy multi-attribute selection among transportation companies using axiomatic design and analytic hierarchy process［J］.Information Sciences，2005，170（2／3／4）：191-210.

［6］SELCUK C，CENGIZ K.Extension of axiomatic design principles under fuzzy environment［J］.Expert Systems with Applications，2010，37（3）：2682-2689.

［7］ZEITHAML V A，BITNER M J，GREMLER D D.Services Marketing［M］.6th ed.New York，N.Y.，USA：McGraw Hill Higher Education，2010：60-70.

［8］BEVILACQUA M，BRAGLIA M.The analytic hierarchy process applied to maintenance strategy selection［J］.Reliability Engineering and System Safety，2000，70：71-83.

［9］TSAI H，HSIAO S.Evaluation of alternatives for product customization using fuzzy logic［J］.Information Sciences，2004，158（1／2／3／4）：233-262.

［10］HUANG H Z，BO R，CHEN W.An integrated computational intelligence approach to product concept generation and evaluation［J］.Mechanism and Machine Theory，2006，41（5）：567-583.

［11］SUN J，KALENCHUK D，XUE D，et al.Design candidate identification using neural network-based fuzzy reasoning［J］.Robotics and Computer Integrated Manufacturing，2000，16（5）：383-396.

［12］SHAPIRO A F.Fuzzy random variables［J］.Insurance：Mathematics and Economics，2009，44（2）：307-314.

［13］TIAN Qihua，XIAO Renbin，ZHONG Yifang，et a1.Evaluation schemes method for design based on information axiom and fuzzy mathematics［J］.Transactions of the Chinese Society for Agriculture Machinery，2008，39（12）：136-140（in Chi-nese）.［田启华，肖人彬，钟毅芳，等.基于信息公理和模糊数学的设计方案评价方法［J］.农业机械学报，2008，39（12）：136-140.］

［14］HOP N V.Solving linear programming problems under fuzziness and randomness environment using attainment values［J］.Information Sciences，2007，177（14）：2971-2984.

［15］SELCUK C，CENGIZ K.Developing agroup decision support system based on fuzzy information axiom ［J］.Knowledge-Based Systems，2010，23（1）：3-16.

［16］DIYAR A，OSMAN K，BRIAN H.Conceptual design evaluation using interval type-2fuzzy information axiom［J］.Computers in Industry，2011，62（2）：138-146.

［17］LIU Baoding，PENG Jin.A couse in uncertainty theory［M］.Beijing：Tsinghua University Press，2005（in Chinese）.［刘宝碇，彭 锦.不确定理论教程［M］.北京：清华大学出版社，2005.］

［18］LIU B D，IWAMURA K.Chance constrained programming with fuzzy parameters［J］.Fuzzy Sets and Systems，1998，94（2）：227-237.

［19］LIU B D，LIU Y K.Expected value of fuzzy variable and fuzzy expected value models［J］.IEEE Transactions on Fuzzy Systems，2002，1（1）：43-63.

［20］General Administration of Quality Supervision，Inspection and Quarantine of the People's Republic of China，Standardization Administration of the People's Republic of China.GB／T9414.8-2001 Guide on maintainability of equipment Part 9：Statistical methods in maintainability evaluation［S］.Beijing：Standards Press of China，1994（in Chinese）.［中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB／T9414.8-2001 设备维修性导则第九部分：维修性评价的统计方法［S］.北京：中国标准出版社，1994.］