基于灰色粒子群算法的飞机装配公差多目标优化设计

张 岩，莫 蓉

（西北工业大学 现代设计与集成制造技术教育部重点实验室，陕西 西安 710072）

0 引言

公差设计是机械制造过程中的一个重要环节，零件的公差属性与其制造过程及产品装配过程紧密相关，决定了产品的性能和制造成本。在传统的产品设计中，公差值大多凭工程师的经验给定，或采用类比、统计等方法得到，这种凭经验定公差值的方法存在数值不准确、不能迅速达到满足产品精度要求、难以获得较低制造成本等问题。航空航天类复杂产品结构复杂、精度要求高，其公差分配工作具有复杂性和重要性。有效的公差分配技术可以在相对较低成本支出的前提下保证产品的良好性能。

针对传统的公差设计方法存在的缺陷，目前公差分配技术的研究主要集中在建立实用的公差设计模型和选用高效的优化求解算法方面。在构建公差设计模型领域，制造成本由于其对公差影响的直观性，常被作为评定设计公差分配合理性的主要准则。文献［1-2］分别论述了几种典型成本—公差模型，主要包括指数模型、平方倒数模型、负幂指数模型、混合模型和多项式模型等。杨将新等提出基于神经网络的加工成本—公差模型［3］，方红芳等提出一种同时考虑加工成本和质量损失的并行公差设计模型［4］。在模型优化求解算法方面，目前主要采用各种智能优化算法，如遗传算法［5］、模拟退火算法［6］、粒子群优化（Particle Swarm Optimization，PSO）算法［7-8］等。其中，文献［6］分别将遗传算法和模拟退火算法应用于公差优化求解问题，得出遗传算法优化结果更优的结论；文献［7］分别应用改进的基于分类排序Pareto 遗传算法（Non-dominated Sorting Genetic Algorithm Ⅱ，NSGA-Ⅱ）和PSO 算法求解相同的公差设计模型，通过计算工作量、效率和可行解数量等评价指标，分析得出PSO 算法在公差设计求解问题上的优势。

上述方法建立了成本—公差的关联模型分析理论，并实现了基于智能优化算法的模型求解方法，为研究公差分配技术提供了可靠依据。但以上方法在构建成本—公差模型的问题上，多面向零件加工成本和工序成本，没有考虑公差对产品装配成本的影响。以飞机制造过程为例，由于飞机结构复杂、零件和连接件数量繁多，飞机的装配过程占据了大量的工时和成本支出，是飞机制造过程的主要环节［9］。因此，装配成本是评价飞机制造成本的重要指标。考虑公差属性对装配过程的影响，面向成本的公差优化设计必须将装配成本引入制造成本模型中加以分析。

本文针对飞机制造过程中常见的装配工艺方法，综合考虑零件加工成本和装配成本，提出一种飞机制造成本—公差模型，进而构建了以制造成本和质量损失为目标的多目标公差优化设计模型。采用灰色关联理论并结合PSO 算法求解公差模型，给出了算法改进策略，使其能够有效地应用于公差模型求解问题。

1 常用飞机装配精度保障方法

在一般机械制造的大批量生产中，为了保证零组件的互换性，主要采用完全互换装配方法，在飞机成批生产中，也希望尽可能多地采用这种方法。但对结构复杂、协调尺寸较多的部位，或在零件、组合件的刚度较小且装配变形无法预先估计的情况下，过分提高零件、组合件的制造准确度和协调准确度，在经济上不合理，技术上也难以达到。因此，在飞机制造过程中大量采用补偿装配方法，通过调整组成环公差的手段降低制造成本，主要包括修配法和装配精加工法等。其中，修配法是对相配合的零件、组合件或部件进行相互修配，需要反复试装和修合，工作量较大，且相互修配后工件不具有互换性；装配精加工是对某补偿环的单独加工或进一步加工，精加工后的工件具有互换性。飞机制造企业装配现场的调研统计表明，在飞机装配过程中，装配精加工方法是目前优先考虑的一种补偿装配方法。鉴于此，本文在研究公差优化设计问题时，重点考虑补偿装配方法中的装配精加工方法对成本—公差模型的影响，同时因为完全互换装配法大量应用于飞机零组件的实际装配过程，所以构建成本—公差模型时应兼顾两种不同方法的适用性。

（1）完全互换装配法 配合零组件组成环公差之和小于或等于装配允许误差，要求任何零组件不再经过修配和补充加工就能满足装配技术要求。

（2）装配精加工 根据规则，在装配尺寸链中选定某一组成环为补偿环，将其他组成环扩大至经济加工公差，通过对补偿环的精加工处理，抵消各组成环的累积误差，最终保证封闭环的精度要求。

补偿环的选择需同时符合以下规则：

（1）根据制造企业的现有制造资源（如设备能力、技工能力等），选择更经济、加工能力易于满足精加工要求的工件作为补偿环。

（2）选择拆装容易的工件作为补偿环。

（3）一般不选择同时属于两个或多个尺寸链的公共环作为补偿环。

（4）同等条件下，优先选择尺寸链中传递比绝对值更大的组成环作为补偿环。

2 多目标公差优化设计模型构建

大多数装配产品的零部件的偏差在装配过程中会不断累积。零件的制造精度越高，最终装配产品的质量就越好，但同时也会产生较高的制造成本。因此，本文以产品制造成本和产品质量损失作为目标进行装配公差的多目标优化设计，使两者权益得到有效均衡，以获得合理公平的公差设计方案。

2.1 制造成本模型

装配产品的制造成本C包括零件加工成本Cm和装配成本Ca两部分，即

为了得到任意精度范围的制造成本与公差的关系式，首先需要进行制造成本—公差建模。对于加工成本与公差的关系，文献［1-2］给出了多种典型的成本—公差模型，为了获得较高的模型精度［10］，本文暂不考虑加工特征对成本曲线的影响，统一采用五次多项式模型作为加工成本—公差模型，表示如下：

式中：a0i，a1i，a2i，a3i，a4i和a5i表示与公差变动相关的加工成本参数；Ti表示第i个组成环的公差；n为组成环个数。

在飞机装配过程中，工装的设计精度根据零件公差属性确定，而技术等级要求、装配设备选择等指标的确定同样与零件的公差属性紧密相关。因此，在分析成本—公差模型时，应充分考虑装配成本与公差的关系。统计实验表明，装配成本—公差模型曲线符合第一象限内的下凹单调递减分布，随着公差变量的增加，成本趋于常量。由于零件公差与装配成本间不存在显式的表达关系，本文采用统计方法，对装配成本与公差属性之间的关系进行量化处理，以便公差优化设计的定量分析。为了得出任意公差范围内的装配成本—公差关系式，首先需要根据预先分析获取的装配成本—公差分布曲线选取合适的数学表达模型，进而依据某些公差值对应的实际成本数据对表达式进行数据拟合，以获取模型参数值。

适用于不同装配方法的装配成本Ca包括常规装配成本Cca和装配精加工成本Cra，即

式中常规装配成本Cca可由泰勒展开式描述为公差的函数，

为保证计算精度与简化计算量，本文采用五次多项式模型构造装配成本—公差模型。因此由式（5）可知，取Cca的麦克劳林级数可得Ccai（Ti）的5次展开式

式中：b0i，b1i，b2i，b3i，b4i和b5i表示与公差变动相关的装配成本参数；ζ表示装配方法系数，采用装配精加工方法时取1，采用完全互换法时取0。在制造资源确定的前提下，装配精加工成本Cra可视为常量。

2.2 质量损失模型

公差是体现产品质量的重要指标，为使产品质量具有可比性，使质量损失成本有一个明确的定义，进而对其进行定量的管理分析，田口玄一博士［11］引入质量损失函数的概念，该方法改善了传统的二值型质量评价方法不能对产品质量进行连续度量的缺陷。因此，本文采用田口二次型质量损失函数表示质量损失—公差模型。假设产品的质量特征值为y，目标值为m，质量损失函数表示为：

式中k为与y无关的质量损失常数。将公差取双向对称分布，则有

装配产品质量特性由装配性能环（封闭环）体现，而封闭环的质量特性由组成环质量特性决定，由式（7）～式（9）可构建装配产品质量损失—公差模型

式中：ki为第i个组成环的质量损失常数；Ti为第i个组成环的公差为合格产品质量特性容许的封闭环公差；A0为产品不合格造成的成本损失；T0为封闭环累积误差。

2.3 公差设计多目标模型

本文以产品的制造成本和质量损失为目标建立多目标公差设计模型，两个目标之间存在“此消彼长”的利益冲突，不可能同时满足各自的最优需求。图1所示为制造成本、质量损失及总成本的经验曲线，可以看出：公差变化导致两目标值的变化趋势完全相反。

多目标公差设计模型需要综合考虑各目标对总成本的影响，以寻找综合成本最优为目标，根据各目标模型求解相对最优的公差设计方案。基于上文对各目标模型的分析，构建如下基于制造成本和质量损失的公差设计多目标模型：

此模型考虑两种不同的装配方法，约束条件分为两种情况：ζ=0时为采用完全互换法约束条件；ζ=1时为采用装配精加工方法约束条件。式中：和表示第i个组成环制造能力满足的有效公差范围边界；和表示第i个组成环经济加工公差范围边界；ξi和ξr分别为带正、负号的组成环和补偿环传递比，正值表示增环，负值表示减环；Ki，K0和Kr分别表示组成环、封闭环和补偿环的相对分布系数；Tr为精加工能力满足的补偿环极限公差，在固定制造资源条件下其值为常量。

3 基于灰色粒子群优化算法的多目标公差优化设计模型求解方法

PSO 算 法［12］是 由Kennedy 和Eberhart 于1995年提出的一种基于群体智能的全局寻优算法。该算法的提出源于群体中个体之间信息的社会共享有助于整体进化的思想。由于它易于理解和实现，在许多优化问题中得到成功的应用，并且在很多情况下被证实比遗传算法等智能优化方法更有效率。但由于单目标和多目标优化问题最优解的更新寻优机制差异，导致标准PSO 算法不能直接用于多目标优化问题。鉴于此，本文提出采用灰色关联理论结合PSO 算法的方法，用于求解多目标公差设计模型。

3.1 粒子群算法原理

PSO 算法中每个粒子都是一个n维矢量，表示一个在n维求解空间中的解，且每个粒子都具有位置和速度两个特征。其中第m个粒子的位置表示为xm=（xm1，xm2，…，xmn），xmi∈［Ln，Un］，Ln和Un分别为搜索空间的下限和上限；速度为vm=（vm1，vm2，…，vmn），vmi∈和分别表示最小和最大速度。用pm=（pm1，pm2，…，pmn）表示粒子m经历的最好位置，种群的全局最优位置记为pg=（pg1，pg2，…，pgn）。算法通过跟踪当前粒子最优解和全局最优解来更新粒子的位置，当达到终止条件时，当前的全局最优解即为所求问题的最优解。粒子在第s+1次迭代的位置通过下式更新获得：

式中：m=1，2，…，N，N为粒子群规模；ω（s）为惯性权重，其大小决定了粒子对当前速度的继承程度，标准PSO 算法取值为1；c1和c2为学习因子，用于调节粒子飞向个体和全局最优位置的步长，标准学习因子取值为c1=c2=2；r1和r2为［0，1］区间上的均匀分布随机数。

针对本文装配公差优化设计问题，将组成环数设置为粒子解空间的维数，各组成环的公差值作为粒子位置分量，粒子搜索空间的上下限及速度取值区间由各组成环的公差取值范围确定。根据式（11）构建目标适应度函数，并求解粒子某状态下的目标值（即某公差设计方案对应的制造成本和质量损失），借助PSO 算法的迭代更新对粒子不同状态下的目标值进行比较，从而获得更优的公差设计方案。

3.2 基于灰色理论的更新寻优机制

PSO 算法的基本流程可简述为四个步骤，即初始化—评价粒子—更新粒子状态—判断终止条件。其中评价粒子环节是PSO 算法迭代寻优的关键环节，其实现方法为：计算粒子的适应值，若其值优于该粒子当前的个体极值，则将pm设置为该粒子的位置，更新个体极值；若所有粒子的个体极值中最好的极值优于当前全局极值，则将pg设置为该粒子的位置，并更新全局极值及其索引号。对于单目标优化问题，粒子极值的评价可通过直接比较目标函数值实现；对于多目标优化问题，由于存在目标间的冲突关系，粒子极值难以通过直接比较方法实现。同样，本文研究的两个公差优化设计目标——制造成本和质量损失分别代表了不同的含义，通过两者数值之和的大小直接比较目标值的优劣并不严谨；而且由于两者函数表达式的不同造成目标值间数量级的差异，直接比较法容易导致“大数”覆盖“小数”，从而削弱“小数”目标的参考价值，形成局部最优，难以获得全局最优方案。针对此问题，本文引入灰色关联理论用于评价粒子极值关系，进而实现迭代过程中粒子的更新寻优。

灰色系统理论是由邓聚龙［13］教授首创的一种系统科学理论，是一种研究少数据、贫信息的不确定性问题的新方法。其中的灰色关联度分析方法是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列间的关联度越大，表示评价对象与目标对象间的相似程度越大，反之越小。根据灰色关联度分析这一品质，考虑本文采用PSO算法进行多目标公差优化设计时，将制造成本与质量损失作为定量指标分析应用于目标适应度函数中，其结果可直接作为灰色关联分析的量化指标进行定量分析。通过对待评价指标序列与基准序列进行关联度分析，评价粒子极值的优劣，从而实现粒子的更新寻优。

选取多目标问题中满足约束条件的各子目标最优适应值，组成基准序列，序列维数由目标个数确定，表示为

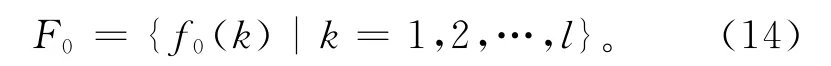
计算粒子每次迭代所得的各目标函数适应值，将其组成待评价指标序列，表示为

则Fi对于F0在k点的灰色关联系数为

式中ρ∈（0，∞）为分辨系数，是预先取定的常数，用于控制关联系数的散布范围。当ρ≤0.546 3时，分辨力最好，通常取ρ=0.5。

因为灰色关联系数是比较待评价指标序列与基准序列在各目标点的关联程度，而对于序列关联度的评价应考虑所有目标点的关联系数综合影响，信息过于分散不便于进行整体性比较，所以将各目标点的关联系数集中表达，在此借助关联系数的加权平均值作为序列关联程度比较的数量表示，平均关联度表示为

式中αk为权重系数，用于表达待评价指标的重要程度，满足。αk越大表明其对应的指标重要程度越高，反之则越低，当各指标同等重要时，作平均权处理。

采用平均关联度表达序列关联程度，认为关联度的大小仅与相关因素序列中各个点关联系数总和有关，没有考虑各点关联系数的差异性。即使点关联系数有明显差异，由式（17）计算得出的平均关联度也可能相同，从而导致实际量化的结果与定性分析相矛盾。鉴于此，将方差引入灰色关联度计算中，通过变异算子反映关联系数序列波动对关联度的影响，用带变异算子的灰色关联度判断待评价指标序列与基准序列的关联程度，其计算公式表示为

通过比较带变异算子的灰色关联度，实现对粒子极值的优劣评价，消除了关联系数存在显著差异而均值相同的序列对关联程度判断的影响，避免了多目标优化问题中出现的早熟局部收敛现象，且采用灰色关联分析方法作为粒子寻优机制具有简单、可靠、易实现的特点。

因为根据灰色关联度值评价待评价指标序列与基准序列的近似程度得出的是相对数值，在算法迭代过程中，关联度数值并非呈规律性趋势变化，所以伴随粒子位置的更新，需将当前状态对应的适应度值和当前全局最优值组成待评价指标序列，分别与基准序列进行关联度计算，并比较相对优劣，关联度值大的为优，反之为劣。

3.3 算法预处理

通过对灰色PSO 算法进行分析，针对公差优化设计模型求解问题，本文给出从粒子初始化条件及惯性权重、学习因子选择两个方面对灰色粒子群求解方法的预处理建议。

（1）粒子初始化

标准PSO 算法的粒子初始化通常采用变量约束区域内的随机生成方法，很容易导致算法前期盲目迭代，降低了寻优效率。因此，本文提出在特定的模型环境下，借助相关规则和知识提前预测可能的最优解位置。考虑在粒子初始化阶段，采用固定解空间中的白化最优解变量，随机生成灰色解变量的方法，以降低算法初期盲目寻优的可能性，提高计算效率。

针对公差优化设计问题，在满足制造成本及制造工艺性要求的前提下，选择传递比绝对值较大、公差变动对目标函数值影响较小的组成环，将其初始公差变量位置选定在公差约束区域的下限附近，即考虑通过收紧对封闭环影响较大的组成环公差，更大限度地放宽其他组成环公差。

（2）惯性权重及学习因子的自适应调节

惯性权重ω（s）的大小决定了粒子对当前速度的继承程度。较大的惯性权重有利于展开全局寻优，较小的惯性权重则有利于局部寻优。因此，本文采用迭代计算过程中呈线性递减的惯性权重，使PSO 算法在开始阶段具有良好的全局搜索性能，能够迅速定位到接近全局最优的区域，而在后期具有良好的局部搜索性能，能够精确地得到全局最优解。线性递减为

式中：smax为最大迭代次数；s为当前迭代次数；ωs和ωe分别表示初始惯性权重和终止惯性权重，一般情况下，可分别取值为0.9和0.4。

学习因子c1和c2的取值范围为［0，4］，标准学习因子取值为c1=c2=2。学习因子决定了粒子本身经验和群体经验对粒子运动轨迹的影响，反映了粒子间的信息交流，设置较大或较小的学习因子值都不利于粒子的搜索。理想状态下，搜索初期要使粒子尽可能地搜索整个空间，而在搜索末期，粒子应避免陷入局部极值。本文采用线性调整学习因子取值［14］，在搜索初期粒子飞行主要参考其本身的历史信息，后期则更注重社会群体信息，取值方法为：

式中：c1s和c2s为初始学习因子，通常分别取值为2.5和0.5；c1e和c2e为 终止学习因子，分别取值0.5和2.5。

采用以上方法确定惯性权重和学习因子取值，随着迭代次数的增加，目标函数值不断接近最优，惯性权重则从ωs线性衰减到ωe，学习因子c1从c1s线性缩小到c1e，c2从c2s线性增大到c2e。该方法符合从全局到局部的寻优策略，实现了迭代过程中粒子的自适应更新。

3.4 基于灰色粒子群优化算法的模型求解流程

步骤1 应用基本PSO 算法分别求解出成本目标函数和质量损失目标函数在约束条件下的最优适应值，将其按一定顺序组成基准序列。

步骤2 设置种群规模，预设算法迭代次数。根据装配尺寸链组成环数，确定粒子解空间变量个数。按照3.3节给出的预处理建议，根据组成环公差约束条件，初始化各粒子的初始位置和速度，并将初始值代入各目标函数，将各适应度值按指定顺序组成初始待评价指标序列。

步骤3 将初始待评价指标序列设置为粒子的个体极值，存储当前粒子位置。计算各粒子的初始待评价指标序列与基准序列带变异算子的灰色关联度，将所有粒子个体极值中与基准序列关联度最高的一个设置为全局极值，并存储其对应的粒子位置。

步骤4 采用式（19）～式（21）更新惯性权重及学习因子，根据式（12）和式（13）更新粒子位置。

步骤5 计算粒子各目标的适应度值，构造待评价指标序列。求解待评价指标序列与基准序列的带变异算子的灰色关联度，并将其与粒子经过的最好位置所对应的关联度进行比较。如果较优，则将当前评价序列更新为个体极值，并存储粒子的当前位置。将所有粒子个体极值的最优值与全局极值进行比较，如果较优，则将该个体极值更新为全局极值，并存储其对应的粒子位置。

步骤6 判断当前迭代次数是否达到结束条件，如果未达到最大迭代次数，则返回步骤4继续搜索；否则，停止搜索，并输出全局极值对应的粒子解变量序列（各组成环的最优公差值）及指标序列（制造成本和质量损失）。

4 实例验证

以某型飞机实验组件为实例，构建面向制造成本和质量损失的公差设计多目标模型，并验证基于灰色PSO 算法的模型求解方法的有效性，组件结构如图2a所示。该组件的装配过程采用定位两插耳向蒙皮装配的路线方法，固定插耳同轴度并作为装配基准，装配准确度要求保证蒙皮外形轮廓度小于0.2mm。装配误差累积沿两条路径由插耳传递至蒙皮外形，装配尺寸链如图2b所示，组成环数据信息如表1所示。假设蒙皮外形轮廓度误差相对分布系数K0=1.44。

表1 组成环数据信息

采用统计方法，分别对加工成本曲线和装配成本曲线进行拟合，获得各组成环成本模型参数如表2和表3所示。由式（10）可知，装配产品质量损失模型可由封闭环质量损失函数表达，本实例封闭环质量损失常数

表2 加工成本模型参数

表3 装配成本模型参数

依据以上提供的模型信息，为了验证灰色PSO算法对公差优化设计求解问题的适用性及本文对算法改进建议的有效性，分别采用本文方法和标准灰色PSO 算法（基本方法）对模型进行求解，算法参数设置如表4所示。首先应用单目标PSO 算法计算约束条件下的制造成本和质量损失目标极值，即在组成环公差范围约束下分别计算出不考虑质量损失的最小制造成本值和不考虑制造成本的最小质量损失值，并将其组成基准序列用于灰色关联寻优，本实例的基准序列为｛10 204.439，1 657.536｝。在本文方法的粒子初始化阶段，依据该实例模型参数，采用3.3节给出的初始化预处理建议，将组成环x5的初始位置预设为0.03（主要考虑收紧公差对目标函数影响较小、尺寸链中对误差累积作用较大等因素），其余组成环对应的初始位置采用随机初始化方法。应用不同方法分别运行一次多目标求解流程，获得的制造成本及质量损失收敛曲线对比效果如图3所示（该曲线为逐次迭代获得的全局最优值变化曲线）。由对比曲线可知，采用本文方法得出的初始目标值、收敛速度、稳健性及最优目标值均优于基本方法，分析结果可以得出以下结论：①预测初始化方法能够保证算法初期目标值最大限度地接近最优目标值，避免盲目迭代，从而提高算法效率；②惯性权重及学习因子的自适应调节能够保证算法的稳健性和收敛速度；③在算法灰色关联度比较寻优阶段引入变异算子概念，能够避免由于均值误差引起的局部最优情况发生，保证算法结果的全局最优性。

表4 算法参数

考虑飞机装配工艺的特点，依据本文建立的适用于不同装配方法的公差多目标优化设计模型，应用改进的灰色PSO 算法，分别选用完全互换装配方法（ζ=0）和装配精加工方法（ζ=1）进行公差优化设计。其中，装配精加工方法根据本文给出的补偿环选取规则，选取组成环x5作为补偿环，假设其精加工能力可达的公差值为0.01mm，根据本实例的制造成本—公差函数计算其精加工成本，并将其代入公差多目标优化设计模型。

为了表征本文算法的稳定性和有效性，在本实例中，分别针对不同装配方法运行本文算法50次，获得的统计结果如表5所示，优化前后设计方案对比如表6所示。

表5 算法多次运行统计数据 元

表5分别列出了算法多次运行统计所得的制造成本和质量损失两个目标值的平均值、最优值和统计误差带宽。由统计数据可知，应用本文算法在多次实验条件下的统计误差较小，误差范围相对可控，算法稳定性良好。表6第一行为该实例组件在优化前依据经验设计的初始公差值及其对应的制造成本和质量损失计算结果。由对比结果可知，本文采用的优化设计方法在保证封闭环质量要求的前提下，大幅降低了该组件的制造成本。同时，通过对两种不同装配工艺方法的设计结果对比可知，对于该类飞机组件，装配精加工方法在收紧补偿环公差的同时，使其他组成环的公差得到放大，由此获得的制造成本和质量损失较完全互换装配方法更低，并保证了组成环零件的互换性。因此，在飞机等大型复杂产品整机装配过程中，对于结构复杂、协调尺寸较多的部位，或在零组件刚度较小的情况下，尽可能采用装配精加工方法，该方法是提高产品装配性能、降低制造成本的有效途径。

表6 公差优化设计前后结果对比

5 结束语

本文以飞机典型装配工艺为背景，将装配成本进行量化处理后引入制造成本模型，全面考虑公差属性对加工成本和装配成本的影响，提出一种基于制造成本和质量损失，并适用于不同装配方法的飞机装配公差多目标优化设计模型。对飞机等复杂装配产品而言，提高了公差设计模型中制造成本目标的精确度和可信度。此外，本文将灰色PSO 算法应用于公差优化设计，并针对公差设计模型求解问题提出了算法改进策略，主要内容包括预测初始化方法、自适应调节惯性权重及学习因子、设置关联度目标权重系数、引入带变异算子的灰色关联度分析等，通过实例分析验证了改进方法的有效性。最后，采用改进的灰色PSO 算法分别对两种典型装配方法对应的飞机装配公差多目标优化设计模型进行求解，并与优化前初始设计数据进行对比分析，验证了模型方法的适用性和有效性。

［1］CHASE K W，GREENWOOD W H，LOOSLI B G，et al.Least cost tolerance allocation for mechanical assemblies with automated process selection［J］.Manufacturing Review，1990，3（1）：49-59.

［2］DONG Z，HU W，XUE D.New production cost-tolerance models for tolerance synthesis［J］.Journal of Engineering for Industry，1994，116（2）：199-206.

［3］YANG Jiangxin，GU Daqiang，WU Zhaotong.Machining cost-tolerance model based on artifical neural network［J］.China Mechanical Engineering，1996，7（6）：41-42（in Chinese）.［杨将新，顾大强，吴昭同.基于神经网络的机械加工—成本模型［J］.中国机械工程，1996，7（6）：41-42.］

［4］FANG Hongfang，HE Yong，WU Zhaotong.Study on concurrent tolerance design based on Taguchi-quality-thinking［J］.Machine Design，1998（3）：22-24（in Chinese）.［方红芳，何勇，吴昭同.基于田口质量观的并行公差设计的研究［J］.机械设计，1998（3）：22-24.］

［5］PRABHAHARAN G，ASOKAN P，RAMESH P，et al.Genetic algorithm-based optimal tolerance allocation using leastcost model［J］.International Journal of Advanced Manufacturing Technology，2004，24（9／10）：647-660.

［6］SINGH P K，JAIN S C，JAIN P K.Comparative study of genetic algorithm and simulated annealing for optimal tolerance design formulated with discrete and continuous variables［J］.Journal of Engineering Manufacture，2005，219（10）：735-760.

［7］SIVAKUMAR K，BALAMURUGAN C，RAMABALAN S.Simultaneous optimal selection of design and manufacturing tolerances with alternative manufacturing process selection［J］.Computer-Aided Design，2011，43（2）：207-218.

［8］XIAO Renbin，ZOU Hongfu，TAO Zhenwu.Multi-objective model of tolerance design and its solution with particle swarm optimization algorithm［J］.Computer Integrated Manufacturing Systems，2006，12（7）：976-980（in Chinese）.［肖人彬，邹洪福，陶振武.公差设计多目标模型及其粒子群优化算法研究［J］.计算机集成制造系统，2006，12（7）：976-980.］

［9］FAN Yuqing.Manufacturing technologies of modern aircraft［M］.Beijing：Beijing University of Aeronautics &Astronautics Press，2001（in Chinese）.［范玉青.现代飞机制造技术［M］.北京：北京航空航天大学出版社，2001.］

［10］WU Zhaotong，YANG Jiangxin.Computer aided tolerance design［M］.Hangzhou：Zhejiang University Press，1999（in Chinese）.［吴昭同，杨将新.计算机辅助公差优化设计［M］.杭州：浙江大学出版社，1999.］

［11］TAGUCHI G，WU Y.Introduction to off-line quality control［R］.Nagoya，Japan：Central Japan Quality Control Association，1985.

［12］KENNEDY J，EBERHART R C.Particle swarm optimization［C］／／Proceedings of IEEE International Conference on Neural Networks.Washington，D.C.，USA：IEEE，1995：1942-1948.

［13］DENG Julong.The basic method of grey system［M］.Wuhan：Huazhong University of Science and Technology Press，1996（in Chinese）.［邓聚龙.灰色系统基本方法［M］.武汉：华中理工大学出版社，1996.］

［14］RATNAWEERA A，HALGAMUGE S.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients［J］.Evolutionary Computation，2004，8（3）：240-255.