基于体分解的MBD 工序模型快速生成方法

赵 鸣，王细洋

（南昌航空大学 航空制造工程学院，江西 南昌 330063）

0 引言

基于模型的定义（Model-Based Definition，MBD）技术详细规定了三维实体模型中产品尺寸、公差的标注规则和工艺信息的表达方法［1］，试图用集成的三维实体模型来完整表达产品定义信息。该技术使三维实体模型作为生产制造过程中的唯一依据，改变了传统的以工程图纸为主、以三维实体模型为辅的制造方法［2］。MBD 工序模型将取代传统的二维工艺卡，实现工艺信息的数字化传递，但人为生成MBD 工序模型的工作量较大。

特征识别技术是计算机辅助设计（Computer Aided Design，CAD）／计算机辅助工艺规划（Computer Aided Process Planning，CAPP）／计算机辅助制造（Computer Aided Manufacturing，CAM）技术集成的纽带和桥梁，也为MBD 工序模型的快速自动生成提供了方法，其关键在于特征识别的效率和准确率。

万能等［3］采用基于图的方法识别出加工特征，通过补特征法与半空间法抑制特征，再由工艺员输入表面加工余量，创建抑制表面特征的实体，然而该方法不能识别不规则几何特征。刘长毅［4］结合体分解和基于图的方法，由图的布尔减运算得到被加工部分，然后逐层分解，再通过特征边界重构最终生成体积特征，但该方法仅适用于2.5 轴加工特征。Kim 等于20世纪90年代初提出立体交替和剖分分解方法［5-6］，对相交特征进行了多种解释，但难以计算带有曲面物体的凸包。Woo等［7-8］对体分解法做了大量研究，在文献［7］中提出通过分解切削体得到最大特征的方法，用平面将切削体一分为二，直到每个体积小于16个面，然后将各体积分解成没有凹边且互不包含的最大体积，并将其组合。该方法虽然分解过程简单，但分解产生的单元体数目很多，且最大特征之间含有大量交集，影响了加工编程效率。文献［8］提出一种基于体分解的方法，该方法对加工零件模型进行简化，直至生成毛坯，所分解出的特征均为最大体积，却没有考虑加工工艺，不是最大加工特征。对最大加工特征进行加工编程，能够有效减少重复走刀的现象。赵鹏等［9］提出一种切削体分解算法，制定了在几何约束、工艺约束下的分割面分解规则和组合策略，该方法能够有效辅助工艺人员进行工艺规划和工序简图绘制。

本文提出一种基于体分解的MBD 工序模型快速生成方法：首先，对包括含曲面的筋特征等加工特征的几何结构进行分析、分类和定义；其次，将切削体分层简化，使用分割面生成方法创建分割面，对复杂相交特征进行分解，以提高体分解效率；再次，根据加工工艺制定单元体组合规则，生成最大加工特征；最后，根据各特征的位置关系制定工艺路线，生成MBD 工序模型。

1 简单零件的体分解

通常，使用编程软件对零件进行加工编程时，首先使用粗加工方法去除尽可能多的体积，系统会对零件进行分层并根据每层的轮廓计算出合理的走刀轨迹，然后再对各个部分进行精加工。对于孔而言，一般遵循先面后孔的原则，孔径较小的单独进行加工，孔径较大的可视为槽进行加工。

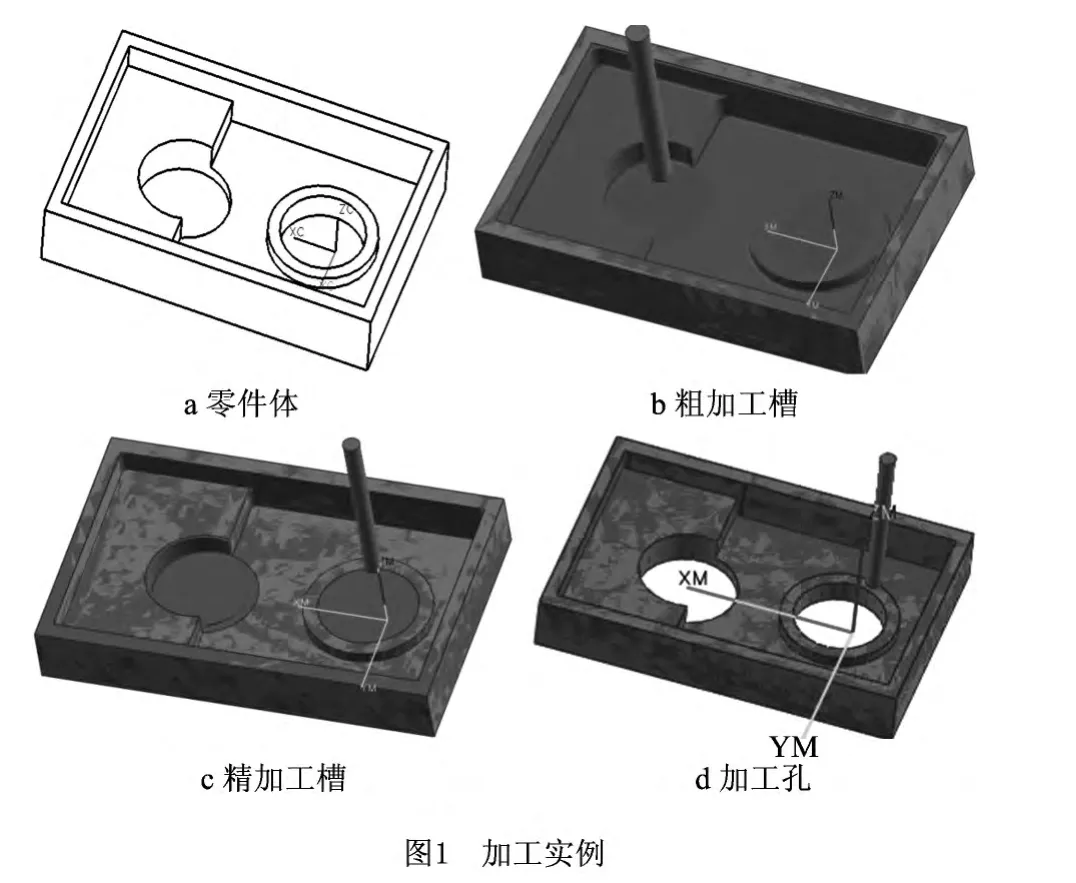
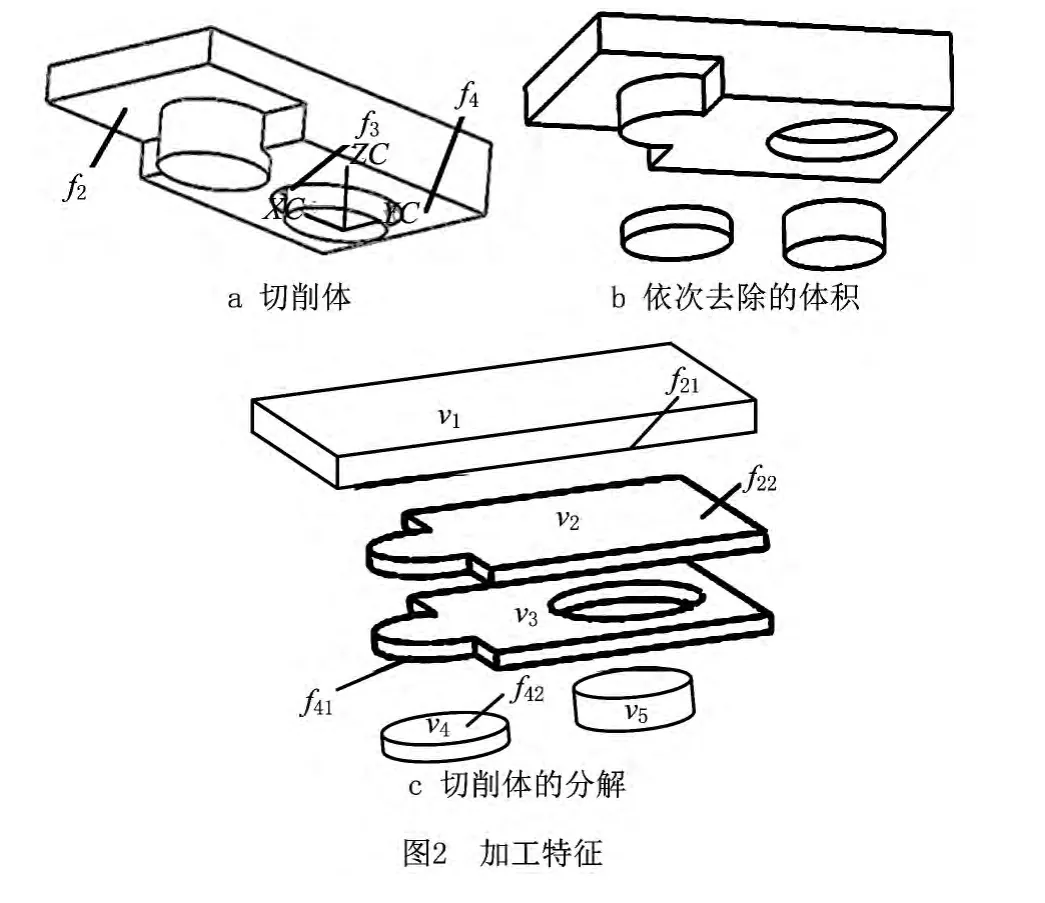
加工实例如图1所示，使用毛坯减去零件体得到的切削体如图2a所示，依次去除的体积如图2b所示，这些体积均为最大加工特征，即一次粗加工可加工出的最大体积。对切削体采用体分解的方法，首先沿加工方向使用一系列平行平面对切削体进行分解（如图2c），然后通过单元体组合得到最大加工特征。特征V1，V2与V3相接触且接触面面积相差不大，可以将其合并；由f4分解体积产生了f41和f42两个面，两个面所在的单元体相接触，但V4为孔特征，因此不执行合并操作。

2 加工特征的分类

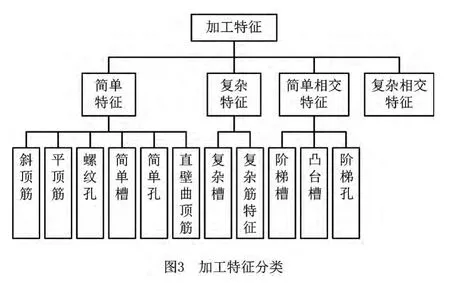
特征识别的意义在于以尽可能简单的方法得到最大加工特征。由于多数零件比较复杂，最大加工特征各不相同，分析其结构，一般为需要单独加工的简单特征、简单相交特征和复杂特征，而加工特征还包括复杂相交特征。加工特征的分类如图3所示。

2.1 简单特征

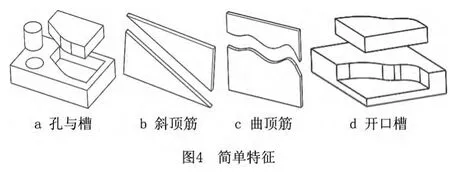
由直线、曲线组成的闭合区间沿其所在平面法向方向拉伸而成的特征为简单特征，这种特征可在三轴数控机床上一次加工出来。简单特征主要包括各种类型槽、孔和部分筋特征，如图4所示。其中单独的槽和孔特征可通过毛坯与零件体的求差运算得到，筋特征则在分离出槽特征后得到。

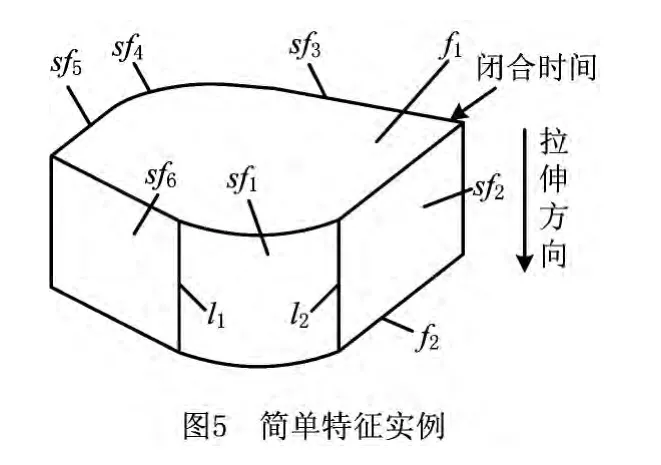
对于切削体，选取能够加工出最多特征的方向作为Z向，记法向为Z向的平面集合为F［10］，并依次编号为F=｛f1，f2，…，fn｝，f1为最先加工的面。垂直于F的平面与柱面［11］集合记为SF，与F成锐角的平面及其他曲面的集合记为XF。记零件面集合为PF，毛坯面集合为MF。各集合中均不包括倒圆面和倒角面等过渡特征，过渡特征的识别与抑制可参考文献［12］。简单特征和简单相交特征记为vs（1，P，Q，N），其中各项依次为特征类型、面集P、面集Q、P面法向N。第一项记槽特征为1，孔特征为2，筋特征为3。

简单特征中两平行平面垂直于其他所有面，其结构如图5所示，用公式表示为

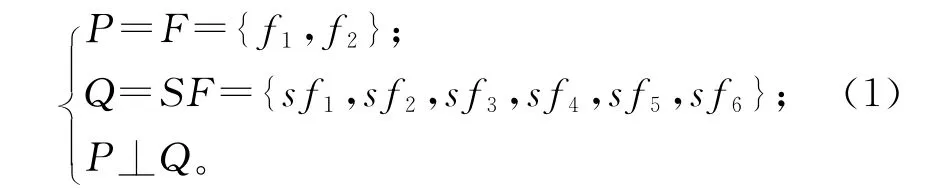
式中：P为垂直于拉伸方向的平面集合；Q为除过渡面外其余面的集合。简单特征中各类子特征的判别条件如下，对于判断错误的个别特征可人为调整：

判别1 当Q中的元素个数｜Q｜=1时，该特征为孔特征。

判别2 若｜Q｜＞1、P中所有面均不与零件接触且拉伸方向不为Z向，则该特征为筋特征，剩余特征为槽特征。

｜Q｜=1时，

｜Q｜＞1时，若∀：sfi（xfi）∈P，sfi（xfi）∩pfj=∅，则，否则Qi，Ni）。

2.2 复杂特征

不能通过拉伸操作生成且不存在凹边的特征，即为复杂特征，如图6所示。复杂特征是将简单特征中的部分面替换为曲面或斜面，增加了识别与加工的难度，这类特征需要特殊的方法进行加工。

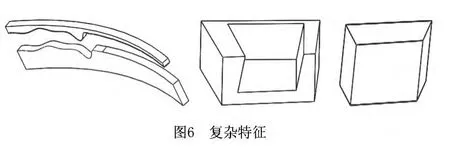
复杂特征记为vc（1，M），其中：第一项为特征种类，复杂槽为1，复杂筋特征为2；M为复杂特征表面集合。子特征的判别条件为：加工方向上的平面fni存在两条小于5mm 的边长，其余的为复杂槽。

若fni∈Mi，∃：l1∈fni，l2∈fni，lenth（l1）＜5，lenth（l2）＜5，则（2，Mi），否则

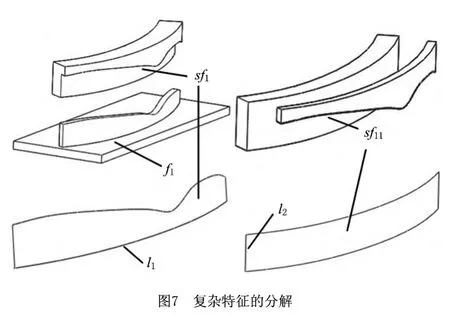
不规则曲面的识别难度较大，很难通过曲面的定义来识别，但可以通过体分解的方式将其分离出来，应用于数控加工编程。图7中使用垂直于平面f1的柱面sf1分解特征，即使用曲线l1沿l2方向拉伸生成曲面进行分解。

2.3 简单相交特征

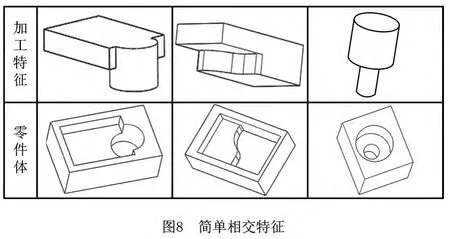
由拉伸方向相同的简单特征相交而成、可分解为两个或多个简单特征的特征，即为简单相交特征，如图8所示。简单相交特征中，集合P中包含的元素个数｜P｜＞2，主要包括槽特征与孔特征的相交。

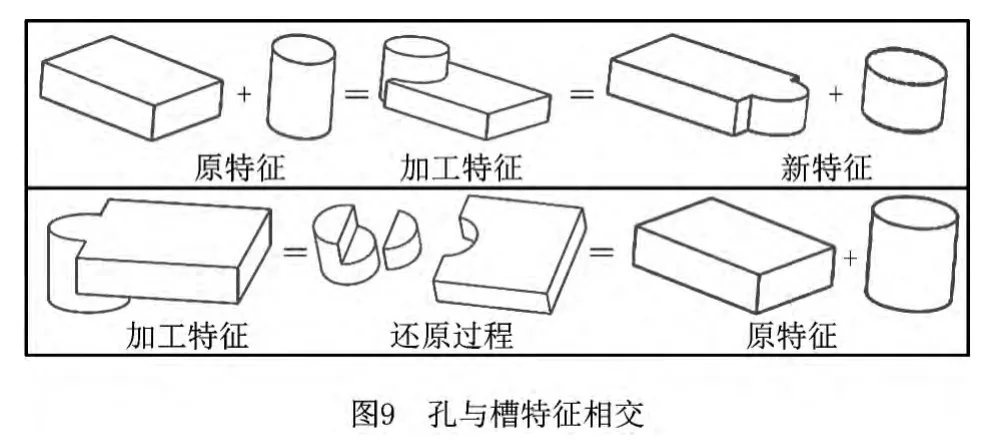
简单相交特征的分解不是将简单特征还原，而是以最简单的方式分解出合理的简单特征。如图9所示，加工特征被分解成新的孔和槽，即可通过加工方向上的一系列平面对原特征进行分解，达到快速分解的目的。若还原成原特征并对原特征进行加工编程，则会有部分刀具路径属于空行程，不但增加了加工时间，而且还原过程比较复杂，需要多次布尔求和。

2.4 复杂相交特征

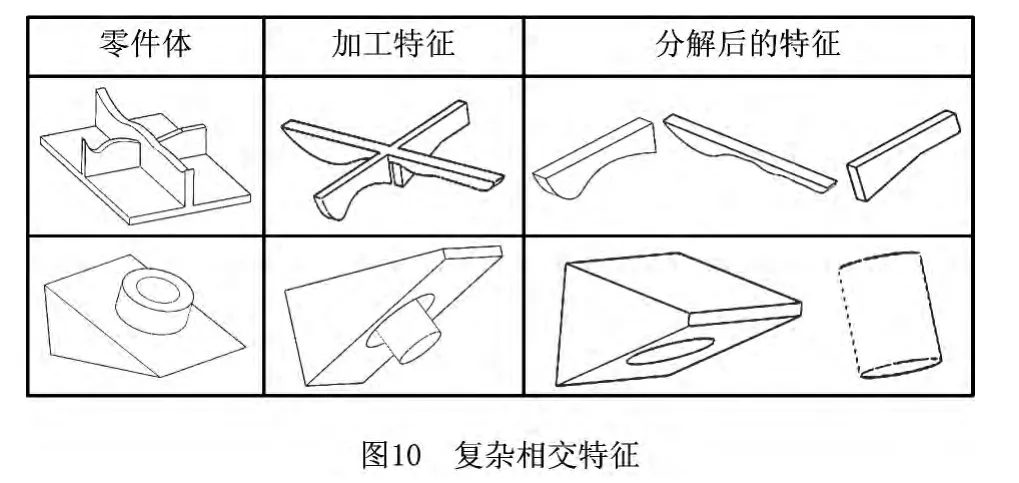
不同拉伸方向的简单特征相交或复杂特征与其他特征相交而成的、较为复杂的特征，即为复杂相交特征。一道工序不能完成复杂相交特征的加工，需要先将其分解为简单特征和复杂特征，然后重组，以生成最大加工特征，如图10所示。

3 体分解策略

针对一个复杂零件的切削体，首先在Z向上对其进行分层处理以简化特征，然后针对各层分别进行分解，得到简单特征和复杂特征，分割面为凹边所属面，最后通过布尔求和运算得到最大加工特征。

3.1 边的凸凹性判别

判定1 直线凸凹性的判定见文献［13］。

曲线只局限于两柱面的交线（空间曲线）或柱面与平面的交线（平面曲线），这是因为柱面可以通过其上曲线的拉伸操作参与特征的分解。

判定2 平面曲线的判定。

任取曲线上的一点，柱面在该点处的切平面与曲线所在平面之间的夹角小于180°时为凹边，反之为凸边。

判定3 空间曲线的判定。

任取曲线上的一点，两柱面在该点处两切平面之间的夹角小于180°时为凹边，反之为凸边。

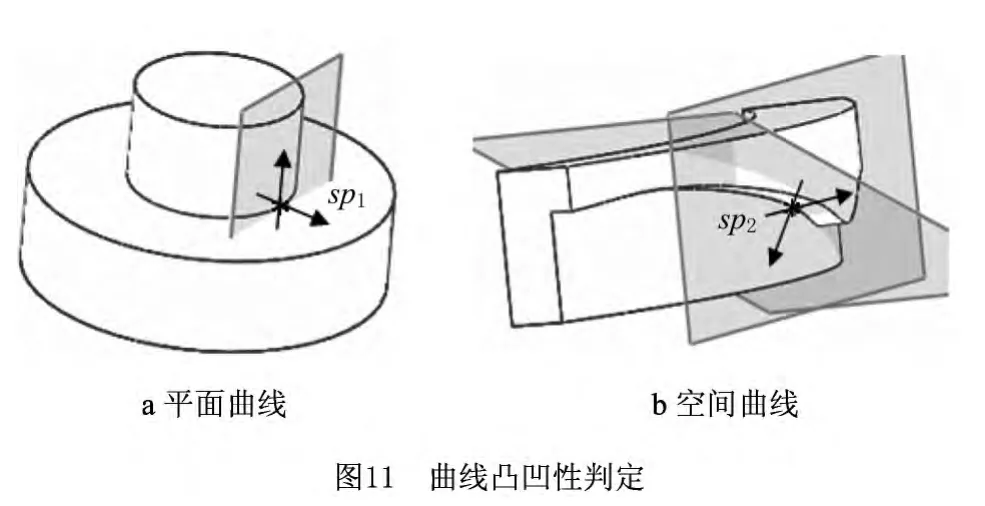
如图11所示，图11a中点sp1处的切平面外法向与平面的夹角为90°，柱面垂直于平面，该曲线为凹边。图11b中点sp2处的两切平面间夹角小于180°，该曲线为凹边。

3.2 分割面的判定及排序

首先分层，若集合F中的元素个数｜F｜=n＞2，则以集合F中的平面｛f2，f3，…，fn-1｝作为分割面，依次分解其所在的体积。

然后判断各特征是否为简单特征，若为简单特征则不再判断凹边，若工艺不符合要求则再由工艺人员分解。编程软件中采用分层加工时可针对各层轮廓生成最优刀轨。

对于非简单特征检索凹边，一条凹边确定一个分割面，即一条凹边确定的分割面仅取具有优先级的面作为生成分割面的基础面，具有同等优先级的面则取两个面。分割面的优先级如表1所示。

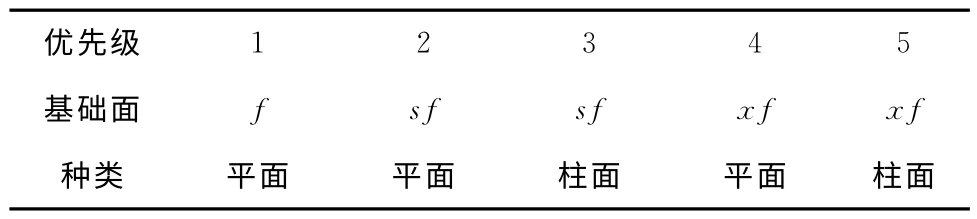
表1 分割面优先级

分割面集合记为DF，元素df（f，NULL，1，0）中的各项分别为基础面、凹边、优先级、分割面生成方式。记：直线型凹边为l，平面曲线型凹边为ep，空间曲线型凹边为es，无凹边记为NULL。分割面的生成方式分为三种，0表示平面自生成，1表示由平面曲线型凹边ep拉伸生成，2表示由柱面上与es对应的平面曲线拉伸生成，如图7所示。

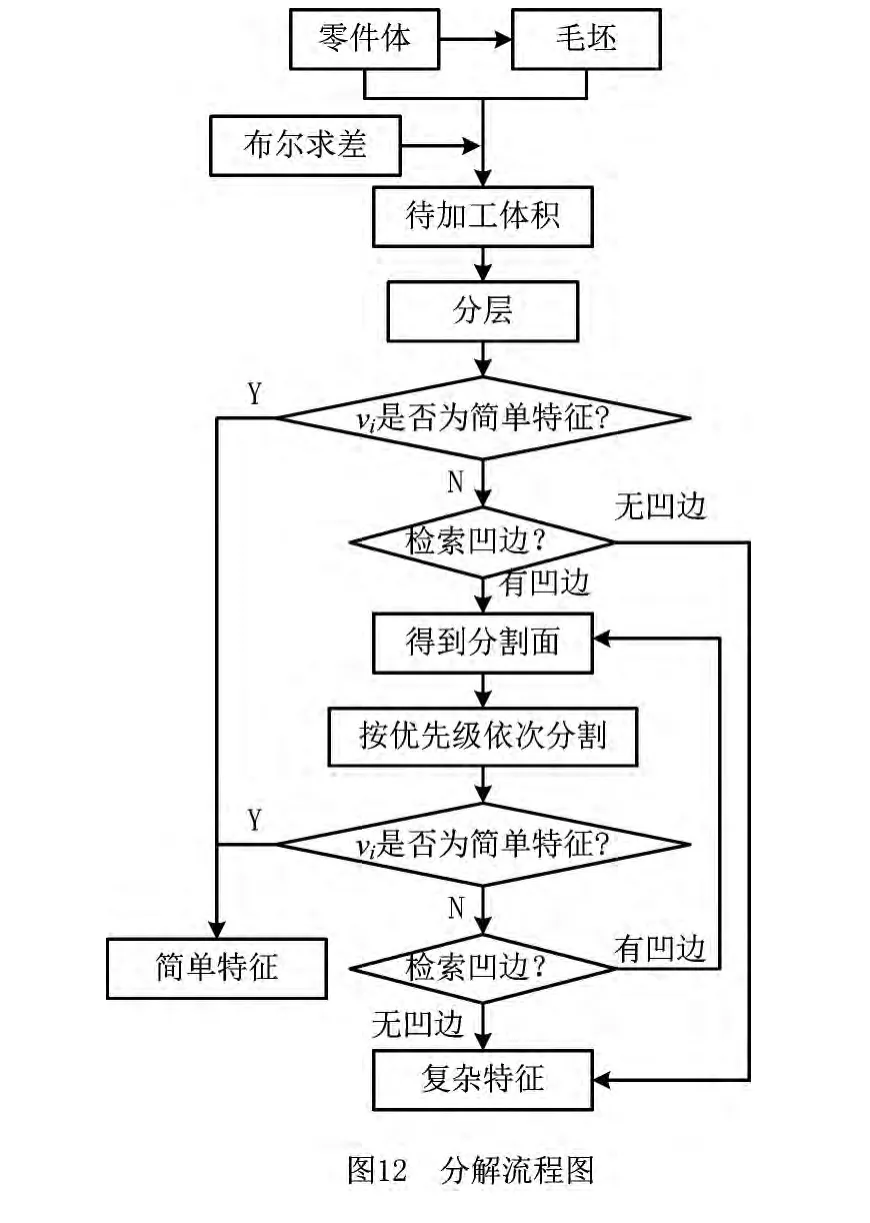
为避免因分割面间的干涉造成特征无意义分割的情况，对所有分割面按照优先级的顺序依次进行分割，且仅对分割面所属的特征进行分割，从而不仅减少了单元切削体的数量，还减少了分割次数，这是因为部分分割面在其他分割面分割后失去了分割作用。同优先级的分割面不用排序。分割完全后仅有简单特征vs和复杂特征vc两种特征。分解流程如图12所示。

3.3 组合规则

分解后，根据各子特征的判别方法判别出各特征类型。

规则1 合并相接触且接触面相等的特征。若∃：fni（sfni／xfni）∈v1，fnj（sfnj／xfnj）∈v2，fni（sfni／xfni）=fnj（sfnj／xfnj），则V1=v1∪v2。

这些特征本属于同一特征。根据前述面的标号方式，fni和fnj由一个分割面分割特征而生成，分属于相邻特征，这样标下标可以大大减少检索次数。

其中k为实数，两槽特征相接触且拉伸方向相同，Sni和Snj为表面积，如果面积相差不大则可选择同一把刀具进行粗加工。

规则3 合并筋特征，得到简单特征。

其中k为实数，如果两筋特征相接触且拉伸方向相同，则可合并为一个筋特征。

按上述三种合并方式依次合并后，即可得到最大加工特征VS和VC。

4 工艺路线及MBD工序模型生成

4.1 工艺路线的生成

采用分层加工的方式，根据各特征中的平面fni最小下标n判断各特征所属层级。若加工方向相同的低层级槽与高层级筋的面相接触，则槽特征加工先于筋特征。同层加工特征的优先级排序如表2所示。同层级同种特征顺序不分先后，属于一道加工工序。

表2 加工特征优先级

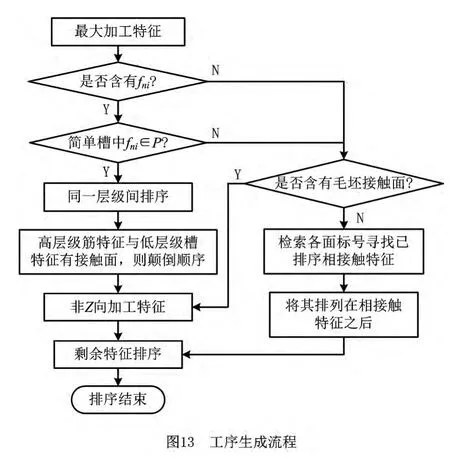
对于不含平面fni的加工特征，含有毛坯面的特征为最优级，其余特征根据面的标号搜索相接触的特征，排在其后。工序生成方法如图13所示。

排序结束即确定了工序加工内容，然后提取加工特征零件接触面的标注信息，再根据特征类型制定加工方案。

4.2 MBD工序模型生成

MBD 工序模型包括几何信息和非几何信息，几何信息即三维几何模型，非几何信息包括制造要求标注、材料属性、加工技术条件和工艺信息等。MBD 工序模型可替代传统的二维工艺卡，作为传递给工人的数字化工艺信息的来源，以满足工人快速、直观地读懂工艺信息的要求，是实现数字化制造的关键；同时，还可以辅助工艺人员完成数控加工编程，其中的非几何信息可减少信息的重复输入。每道工序都对应一个MBD 工序模型，因此多个工艺人员可同时对同一零件的不同工序进行数控编程，从而提高零件的编程效率。

5 体分解实例

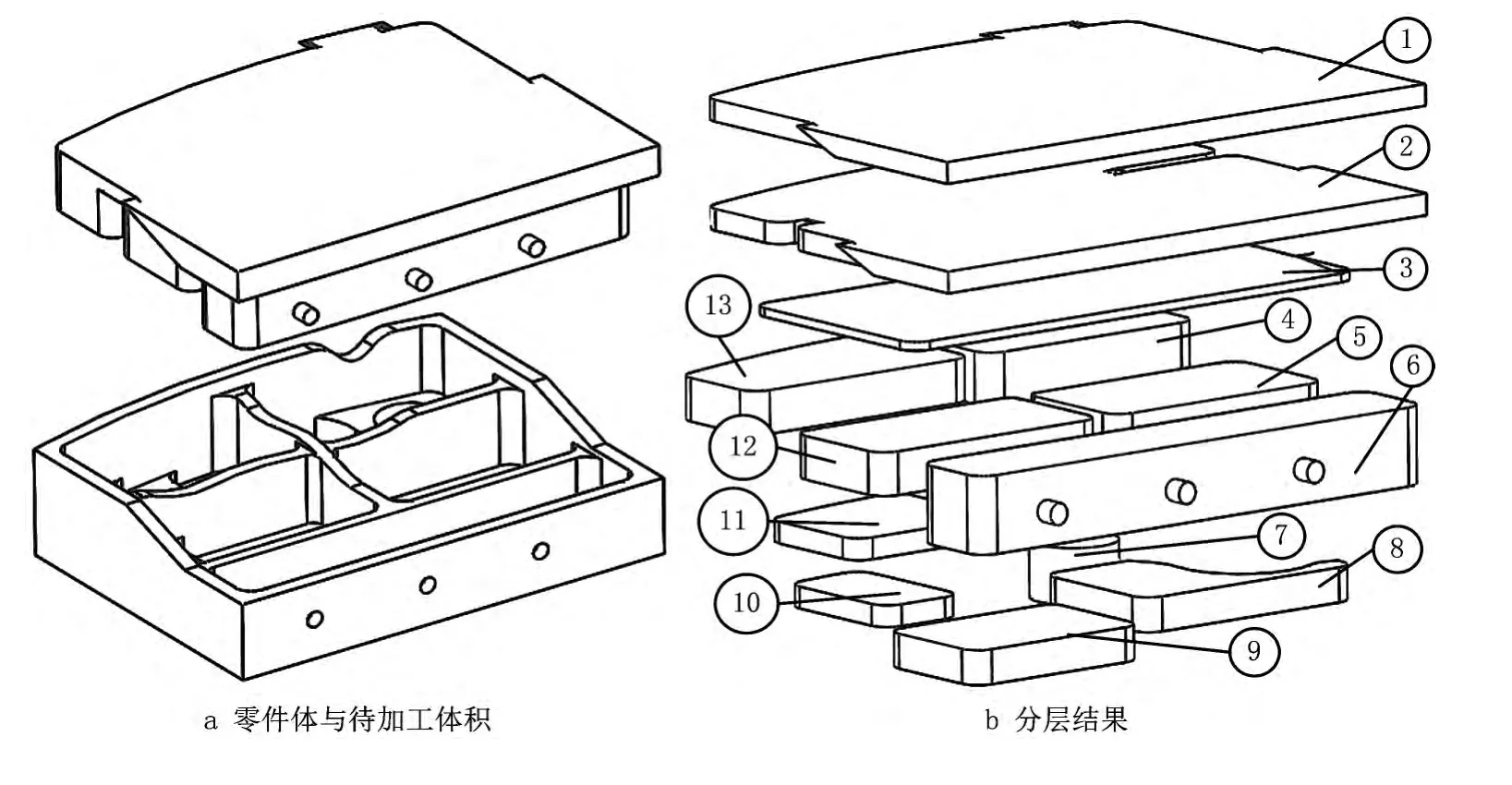
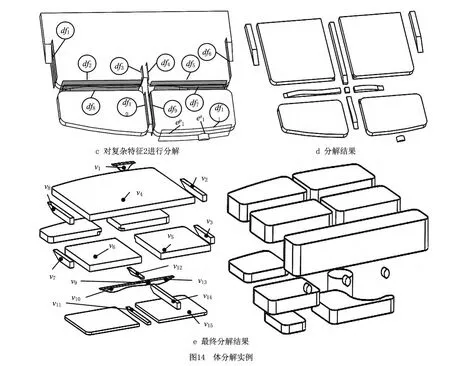
根据以上步骤，零件分解过程如图14所示。图14a为零件模型与待加工体积，待加工体积由毛坯减去零件体生成。图14b为分层操作结果，使用一系列法向为加工方向的平面依次分割其所属体积，能够避免整体分割常出现的误分割问题，由此生成的简单特征均有意义。图14b中的复杂相交特征只有1，2，3，6，只针对这些特征进行进一步分割操作即可。以复杂相交特征2的分解为例，如图14c所示：检索凹边，得到凹边所在的分割面df1，df2，…，df11，其中df1和df6由直线型凹边所属的平面生成，df11由柱面上与对应的平面曲线拉伸生成，其余分割面均由平面曲线凹边所属平面生成。根据分割策略，若首先使用df3和df4进行分割，则df9和df10会失去分割作用，减少了分割次数。最后使用df11进行分割，分割结果如图14d所示。按同样方式分割其他复杂相交特征，得到最终的分割结果如图14e所示。

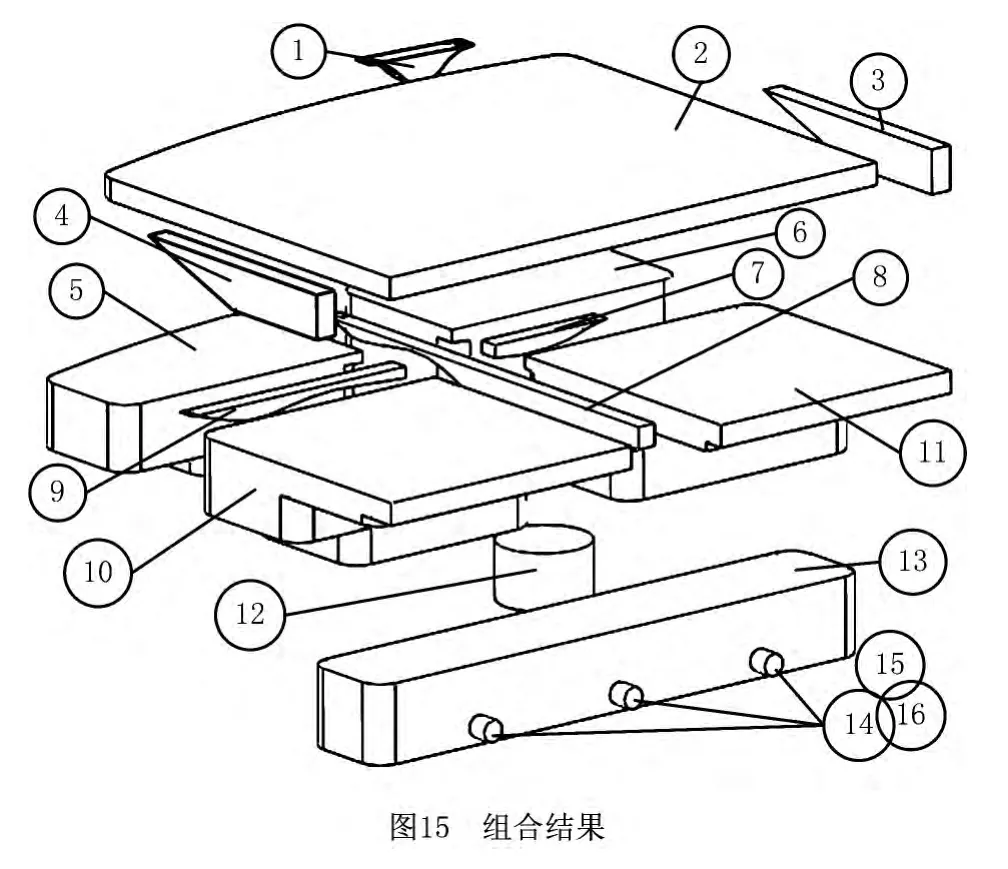
依照组合规则对图14e中的所有特征进行合并，记“+”为布尔求和运算符，其中按照规则1执行v2+v3，v7+v8，v9+v10+v13等，按照规则2执行v5+v15等，按照规则3执行v11+v14等，最终得到的特征均为最大加工特征，如图15所示。

第一步分层得到13个特征，第二步分割后得到31个特征，其中被分割的单元体只有图15 中的特征1，3，4，8，其余单元体均可作为单个特征用于编程。为了工艺的需求，进行求和运算后最终得到16个最大加工特征。

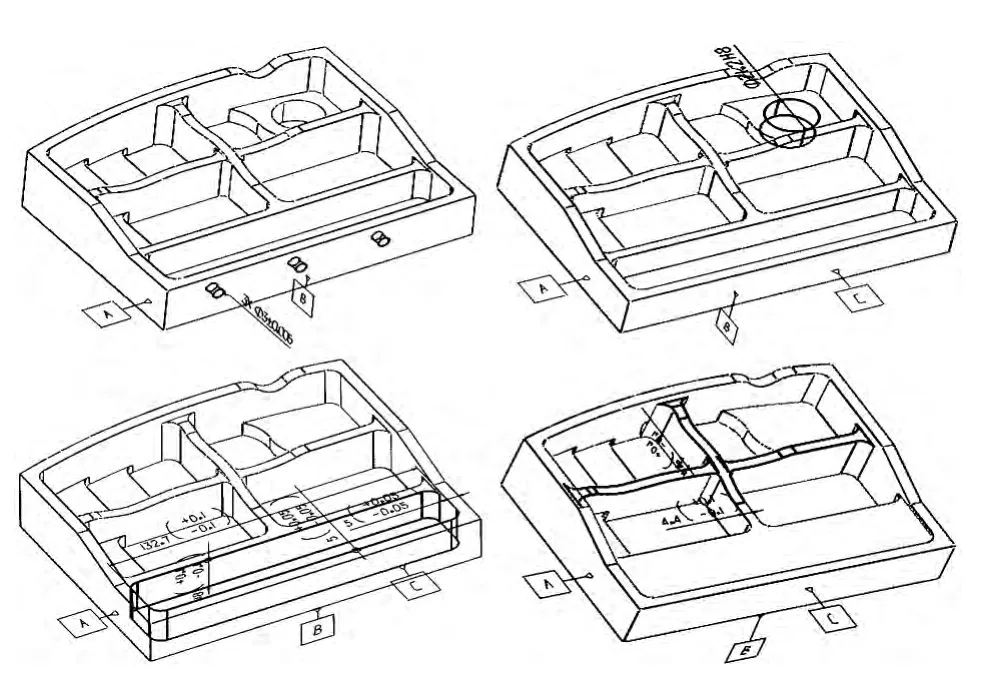
根据前述工序生成方法，生成该零件加工工序如表3所示。根据工序内容，使用逆序的方式生成每道工序的MBD 工序模型如图16所示，其中颜色加深部位为待加工部位，图中仅显示了部分非几何信息。

表3 加工工序

6 结束语

本文从零件的加工工艺出发，归纳总结了各种常见的加工特征，用新的分类方式概括了大多数加工特征，明确了特征识别的方向和目标。提出了一种能识别出最大加工特征的体分解方法，包括含有曲面的筋特征的识别。其中分割面的生成与排序能够减少单元体数目的生成，提高特征识别的效率。提出了工艺路线生成方法，将最大加工特征进行排序，生成加工工序，并实现了MBD 工序模型的快速生成。根据最大加工特征自动生成工艺信息与切削参数等，是进一步的研究内容。

［1］ZHOU Qiuzhong，FAN Yuqing.Application of MBD on airplane manufacturing［J］.Aviation Maintenance &Engineering，2008（3）：55-57（in Chinese）.［周秋忠，范玉青.MBD 技术在飞机制造中的应用［J］.航空维修与工程，2008（3）：55-57.］

［2］QUINTANA V，RIVEST L，PELLERIN R，et al.Will modelbased definition replace engineering drawings throughout the product lifecycle？aglobal perspective from aerospace industry［J］.Computers in Industry，2010，61（5）：497-508.

［3］WAN Neng，GOU Yuanjie，MO Rong.A new feature recognition design method for MBD rough model［J］.Journal of Com-puter-Aided Design &Computer Graphics，2012，24（8）：1099-1107（in Chinese）.［万 能，苟园捷，莫 蓉.机械加工MBD毛坯模型的特征识别设计方法［J］.计算机辅助设计与图形学学报，2012，24（8）：1099-1107.］

［4］LIU Changyi.Machining feature recognition based on graph volume decomposition［J］.Computer Integrated Manufacturing Systems，2006，12（7）：1013-1017（in Chinese）.［刘长毅.基于图的体积分解的加工特征识别方法［J］.计算机集成制造系统，2006，12（7）：1013-1017.］

［5］KIM Y S.Recognition of form features using convex decomposition［J］.Computer-Aided Design，1992，24（9）：461-476.

［6］WANG E，KIM Y S.Form feature recognition using convex decomposition：results presented at the 1997ASME CIE feature panel session［J］.Computer-Aided Design，1998，30（13）：983-989.

［7］WOO Y，SAKURAI H.Recognition of maximal features by volume decomposition［J］.Computer-Aided Design，2002，34（3）：195-207.

［8］WOO Y.Automatic simplification of solid models for engineering analysis independent of modeling sequences［J］.Journal of Mechanical Science and Technology，2009，23（7）：1939-1948.

［9］ZHAO Peng，SHENG Buyun，DENG Weigang.Delta volume decomposition and combination strategy for process planning［J］.Computer Integrated Manufacturing Systems，2010，16（9）：1793-1800（in Chinese）.［赵 鹏，盛步云，邓伟刚.工艺设计过程中的切削体分解组合策略［J］.计算机集成制造系统，2010，16（9）：1793-1800.］

［10］CHEN Z M，GAO S M，LI W D.An approach to incremental feature model conversion［J］.Advanced Manufacturing Technology，2007，32（1／2）：99-108.

［11］SUNDARARAJAN V，WRIGHT P K.Volumetric feature recognition for machining components with freeform surfaces［J］.Computer-Aided Design，2004，36（1）：11-25.

［12］SUN Rui，LI Ming，GAO Shuming.Algorithm for suppressing blend features based on volume reconstruction［J］.Computer Integrated Manufacturing Systems，2011，15（6）：1149-1156（in Chinese）.［孙 锐，李 明，高曙明.基于体重构的过渡特征抑制算法［J］.计算机集成制造系统，2011，15（6）：1149-1156.］

［13］GUAN Wentian.Feature model conversion of CAD／CAPP integrated system［D］.Xi'an：Northwestern Polytechnical University，2001（in Chinese）.［关文天.CAD＿CAPP集成系统特征模型转换技术研究［D］.西安：西北工业大学，2001.］