三轴高g压阻式微加速度计的设计

林 杰，林立伟，郭 航

（厦门大学萨本栋微米纳米科学技术研究院，厦门大学物理与机电工程学院，福建 厦门361005）

在过去的20年，基于硅微加工技术的传感器已应用于各种传感测量，如压力、应力和加速度［1］.其中，压敏电阻微加速度计在车辆碰撞试验、安全控制和引信系统［2］中发挥着越来越重要的作用.而对微加速度计的性能要求也越来越高，如冲击环境下的加速度要求达到100 000 g以上［3］，弹药制导化中要检测从几g到上万g的加速度［4］，因此需要研发高g且性能优良的微加速度计.运用微机电系统技术制造的硅微加速度计具有灵敏度高、线性度好、谐振频率高等优点.孟美玉等［5］在理论上分析了三轴压阻式微加速度计的结构参数对应力、频率的影响，但对于灵敏度和应力的关系尚未分析清楚，也未进行有限元软件ANSYS的仿真分析；石云波等［6］设计了一种基于绝缘层上的硅（SOI）的三轴压阻式微加速度计，但结构设计中未考虑梁的惯性力，也未对器件的灵敏度和线性度进行详细的探讨.针对高g压阻式加速度计固有频率低、输出信号有谐振的现象［7］，设计具有较高固有频率的微加速度计，使其能满足高g环境的要求具有重要的意义，而压阻式微加速度计的理论和仿真分析中［4，6］，大部分未对电阻的布置进行详细的探讨，所以改变电阻的位置来提高加速度计的性能也具有很大的必要性.

1 结构设计

1.1 应力和频率的推导

如图1（a）为三轴八梁压阻式微加速度计的一般结构，外边框为固定端，中间为质量块，两部分通过悬臂梁连接.当对称结构上受对称载荷作用时，在对称截面上，反对称内力即剪力等于0，但是弯矩不为0.微加速度计关于对角线对称，则可以简化为一次静不定问题，即一个仅有单根悬臂梁和1／8质量块的结构简化模型，如图1（b）所示.因梁的变形引起的应力不能被忽略，梁的惯性力应该考虑进去，其力学简化模型如图1（c）所示，其中，P1和P2分别是图1（c）中梁和质量块的惯性力，F和M是固定端的反力和弯矩，Mx为截面上的弯矩.而

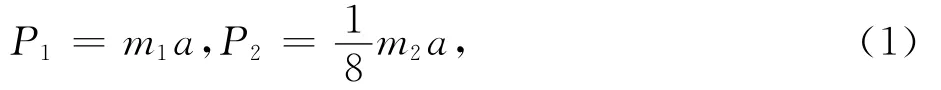
其中，m1和m2分别为单梁和整个质量块的质量，a为加速度.

假设在Z方向加载加速度，且质量块必须视为刚体，X方向上梁和质量块的弯矩方程为：

其中，l1是悬臂梁的长度，l2是质量块的半长，E是弹性模量，I1是单梁关于Z轴的惯性矩.

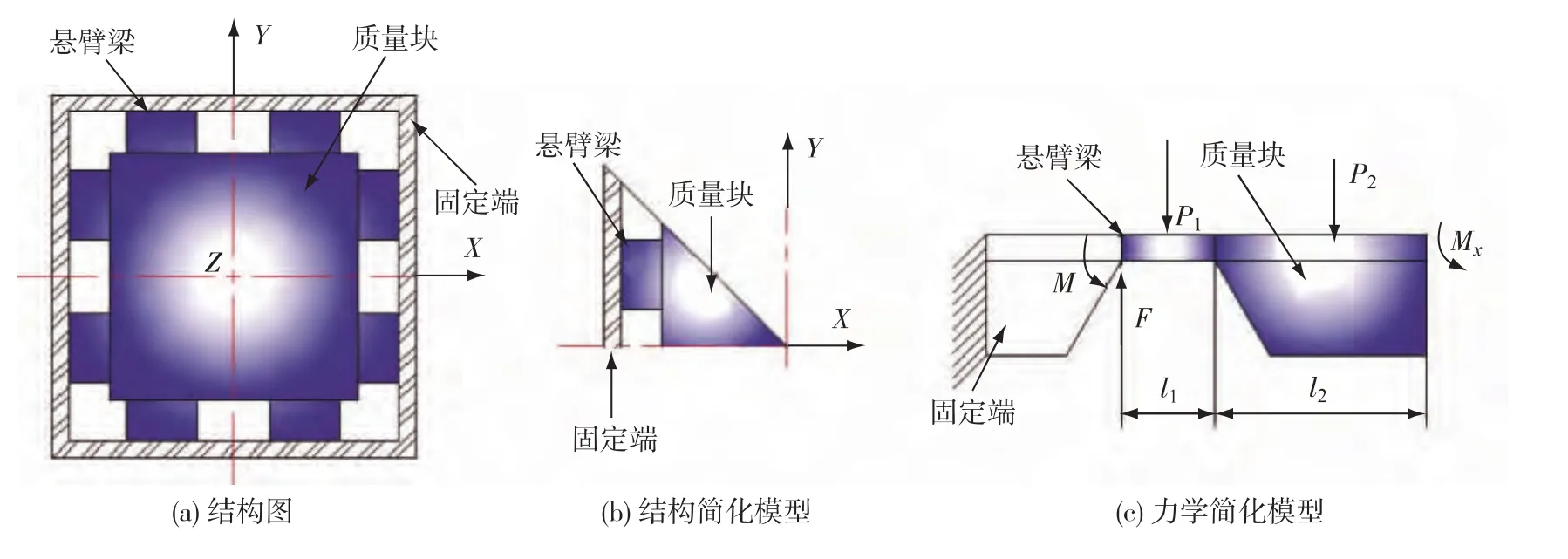
图1 加速度计的结构图Fig.1 Structural diagram of accelerometer

通过力法正则方程，使用莫尔积分求对称截面上的弯矩Mx，可得：

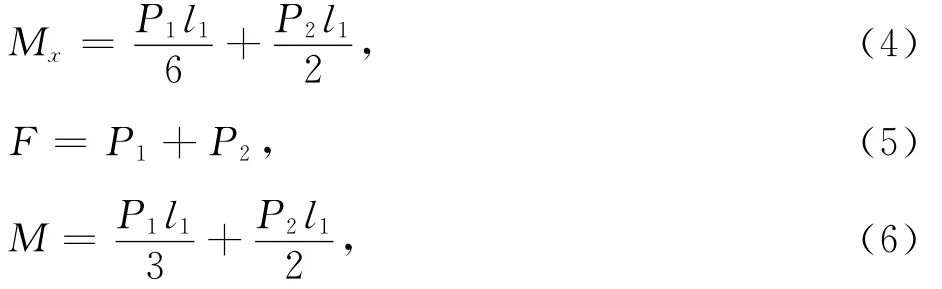
代入式（2），则可化为：

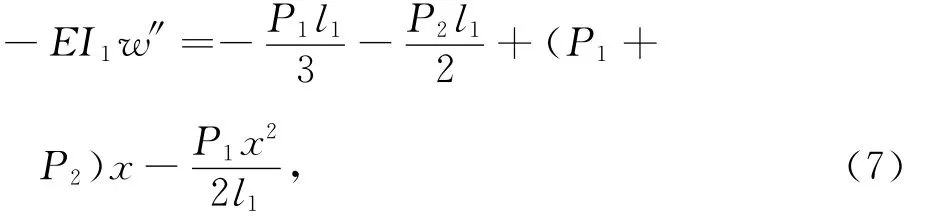
根据边界条件积分式（7）求弯曲挠度得：

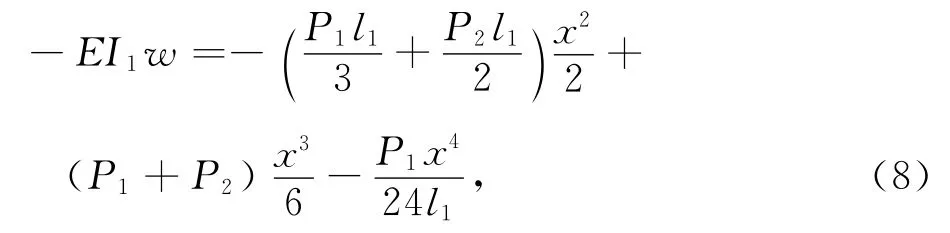
梁截面上的弯曲正应力为：

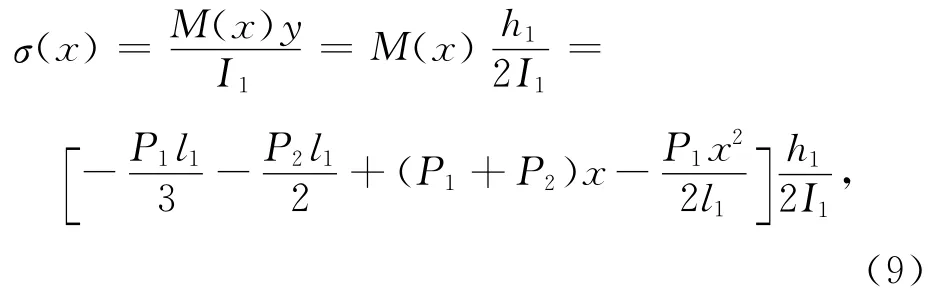
则梁截面上的最大弯曲正应力应在x＝0处：

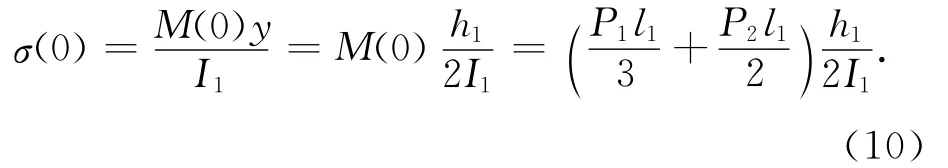
通过Rayleigh－Ritz法［8］，求得最低的固有频率：

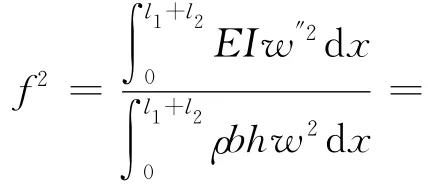
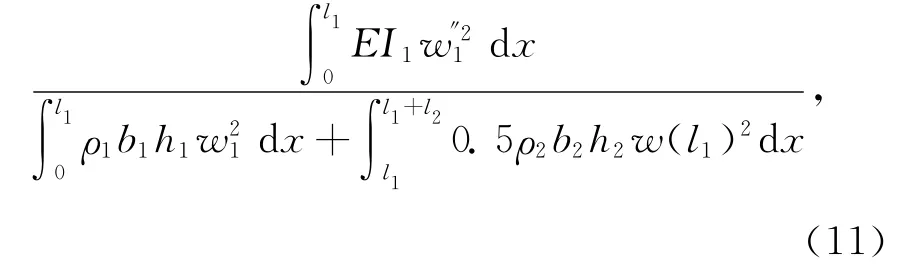
其中，ρ1和ρ2分别为梁和质量块的密度，b1和b2分别为梁和质量块的宽，h1和h2分别为梁和质量块的厚.这里加速度a取200 000 g，将式（7）和式（8）代入式（11）即可求得一阶的固有频率.

根据微型化和加工工艺的要求，质量块的大小被限制为2 200μm×2 200μm×400μm，梁的厚度限制为100μm，因此P2已确定.根据式（10），可得梁的宽度、长度和截面上的最大弯曲正应力之间的关系如图2所示；同样，根据式（11），可得梁的宽度、长度和一阶固有频率之间的关系如图3所示.

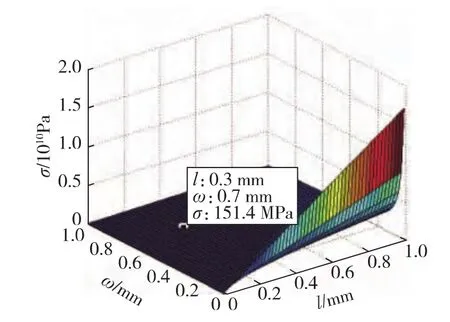
图2 梁长度、宽度和最大弯曲正应力的关系Fig.2 Relationship between maximum bending stress and length or width of beam

从图2～3可以看到，随着梁长度的增加，最大应力逐渐增大，固有频率迅速减少，因此减小梁的长度可以显著增大固有频率，同时减小最大应力.随着梁的宽度的增加，最大应力迅速减少，固有频率逐渐增大，所以增大梁的宽度可以减小最大应力，同时提高固有频率.不过，减小最大应力的同时也会降低灵敏度的大小.

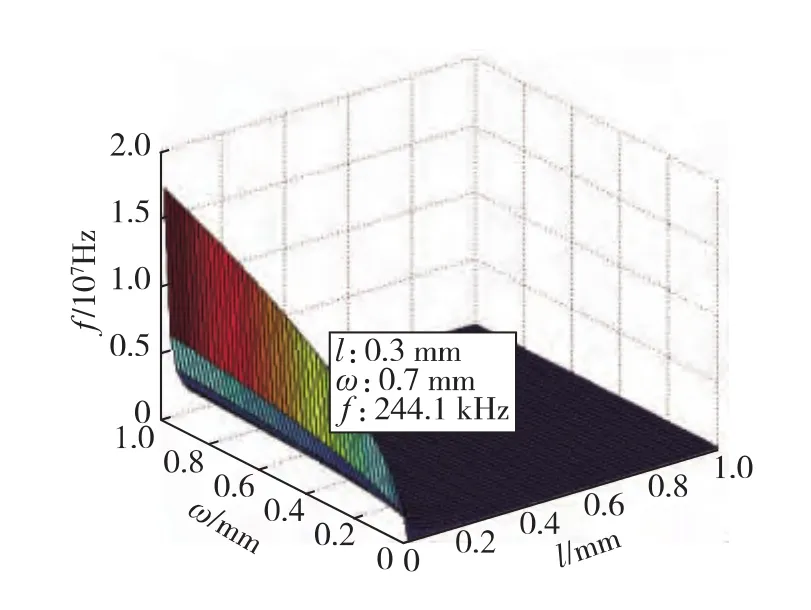
图3 梁长度、宽度和一阶固有频率的关系Fig.3 Relationship between first－order natural frequency and length or width of beam

综合考虑最大应力、固有频率和灵敏度等因素后，确定微加速度计的参数如表1所示.把参数代入以上方程，求得最大弯曲正应力为151.4MPa，一阶固有频率为244.1kHz.

对于硅的微机械结构中的断裂应力有不少研究，因研究对象、手段与方法的不同，所得的值有所差异，大致为1.0～3.3GPa［9－10］，远大于最大弯曲正应力151.4MPa，满足强度条件，同时又有较高的一阶固有频率以承受高频信号冲击.

表1 结构参数Tab.1 Structure parameters

表2 模态频率Tab.2 Modal frequencies

1.2 应力和频率的仿真分析

利用ANSYS软件建立该微加速度计的三维有限元模型，硅材料的密度为2 330kg／m3，杨氏模量为130GPa，泊松比为0.278，整个微加速度计网格划分的单元类型为三维固体结构Solid185.

在外边框施加全约束后，在Z轴上加载一个200 000 g的加速度，分析得Mises等效应力如图4所示，最大等效应力发生在梁和质量块的交界处，大小为261MPa，也远小于硅的断裂应力，亦满足强度条件.一阶模态如图5所示，其一阶固有频率为227 kHz，与理论结果244.1kHz非常接近，验证了理论公式.而前5阶模态下的固有频率如表2所示，说明该高g微加速度计的高阶频率值也很大.

为了分析其他方向的应力情况，在X轴上加载一个200 000g的加速度，得到的Mises等效应力最大为91.1MPa，可知相同加速度负载下X轴方向的灵敏度会较小.

由于理论计算结果为截面上的弯曲正应力，仿真结果为Mises等效应力，故最大点不同.于是在梁与外边框的交界线进行路径仿真分析，求得分界线上的最大应力为165MPa，与理论结果151.4MPa也基本一致，亦验证了理论公式.以上结果也表明该微加速度计具有较好的力学性能.

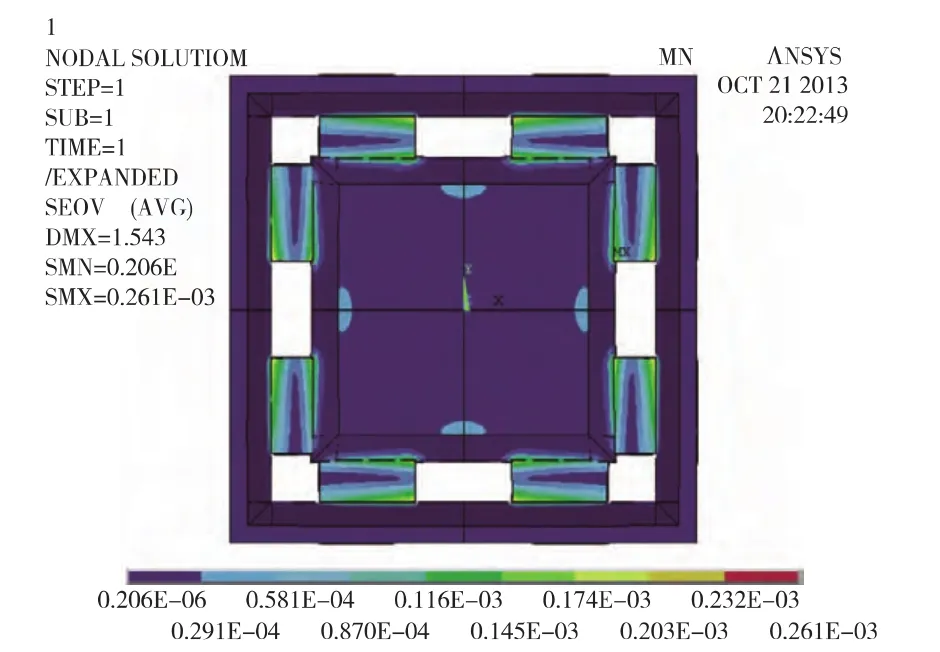
图4 Z轴加载时的等效应力Fig.4 The equivalent stress when loaded in Z

图5 一阶振动模态Fig.5 1st vibration mode shape

2 压敏电阻的布置

2.1 输出电压

压敏电阻在［011］和［011］晶向上的电阻变化率［4］为：

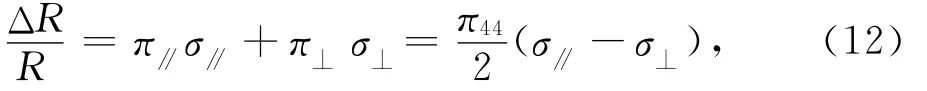
其中，π∥和.π⊥为纵向和横向压阻系数，σ∥和σ⊥为纵向和横向应力，π44为P型硅的剪切压阻系数，由掺杂浓度和温度决定，根据工艺条件，取138.1×10－11Pa－1.

如图6所示，通过恒压源均输入电压Ui＝5V，Z轴全桥电路的输出电压为：

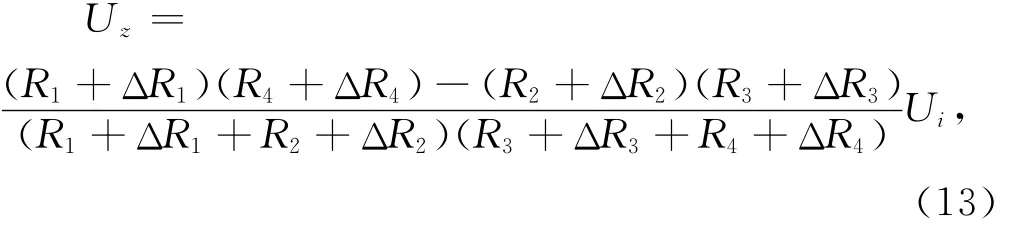
X轴的半桥电路输出电压（Y轴与X轴类似）为：

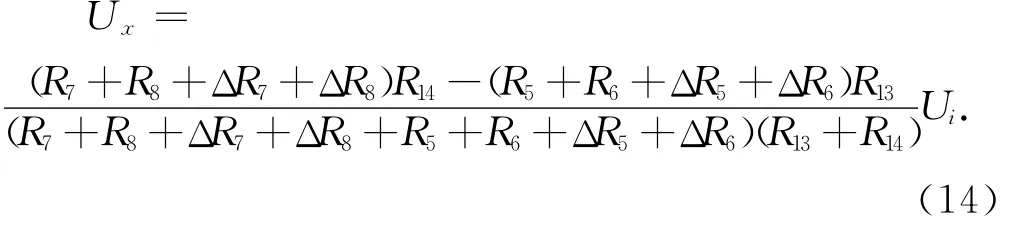
微加工中使R1＝R2＝R3＝R4＝R，如图7布置电阻，则在Z轴上加载时ΔR1＝ΔR4和ΔR2＝ΔR3，全桥电压为：

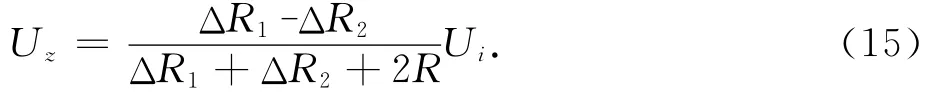
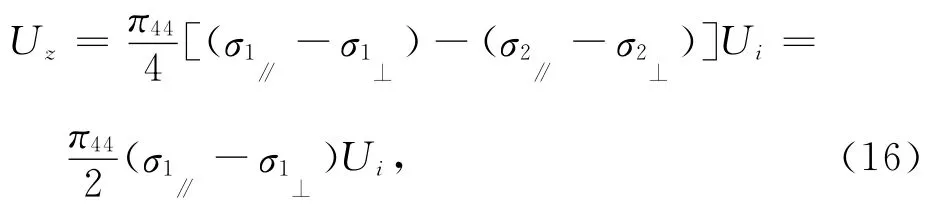
其中，σ1∥和σ1⊥为电阻R1的纵向和横向应力，σ2∥和σ2⊥为电阻R2的纵向和横向应力.

同理微加工中使R5＝R6＝R7＝R8＝R13＝R14，R9＝R10＝R11＝R12＝R15＝R16，其中R13、R14、R15、R16为定值电阻，布置在任意适当的位置均可，如图7在X轴上加载时ΔR5＝－ΔR7＝ΔR，在Y轴上加载时ΔR9＝－ΔR11＝ΔR，则根据式（12）和式（14），X、Y 轴的半桥电压为：

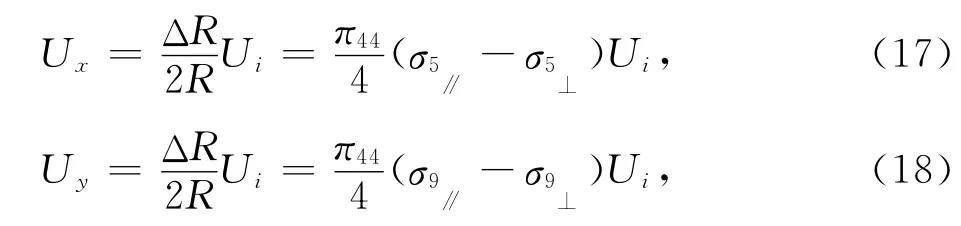
其中，σ5∥和σ5⊥为电阻R5的纵向和横向应力，σ9∥和σ9⊥为电阻R9的纵向和横向应力.由此也可以看出相同应力差负载情况下，全桥电路的输出电压是半桥电路的2倍.

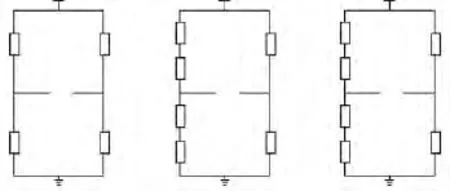
图6 惠斯通电桥Fig.6 Wheatstone bridge

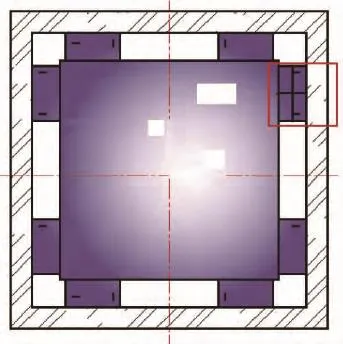
图7 电阻的布置Fig.7 Layout of varistors

2.2 电阻位置的仿真分析

根据如图7所示的布线图，把Z轴的4个力敏电阻对称布置在4条边上的［011］晶向，且靠近梁端部；把X轴的4个力敏电阻对称布置在X轴方向的4个梁上的［011］晶向；把Y轴的4个力敏电阻对称布置在Y轴方向的4个梁上的［011］晶向.

从式（16）～（18）可知，输出电压与横纵向应力差成正比，因此通过ANSYS软件分析电阻的应力差即可求得输出电压.由于8梁结构的对称性，选择任意一个悬臂梁（图7中方框标出）研究其应力.先选择水平方向的一个梁的中线作为路径1分析其应力，如图8所示（原点为路径的最左端）.接着选择该梁的竖直方向作为路径2进行应力分析，如图9所示（原点为路径的最下端）.图中σx、σy、σDETA分别为横向应力、纵向应力、应力差.

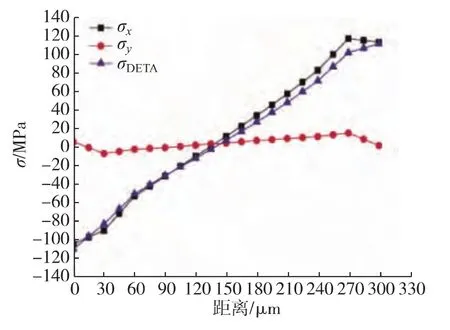
图8 路径1的横纵向应力及其差值Fig.8 Stresses and difference along path1

图9 路径2的横纵向应力及其差值Fig.9 Stresses and difference along path2

为了保证输出的线性度，电阻必须布置在远离非线性的区域；同时，电阻应该靠近梁的末端以获得较大的表面应力差.从图8可以看出，梁中间区域的应力关系接近线性.所以电阻布置在距离右末端60～120μm的区域.从图9可以看出，距离上下端100μm处的应力差较大，所以选择该区域来布置电阻.

3 三轴的灵敏度和线性度

3.1 三轴的灵敏度

同图4通过ANSYS软件在Z轴加载200 000 g的加速度，求R4的横纵向应力及其差值，通过仿真和计算求得应力差的平均值为46.68MPa.而类似图4，在X轴加载200 000 g的加速度，求R7处的横纵向应力及其差值，得应力差的平均值为17.66MPa.

将Z方向的差值代入式（16），求得输出电压为161.16mV，则Z方向的灵敏度为：

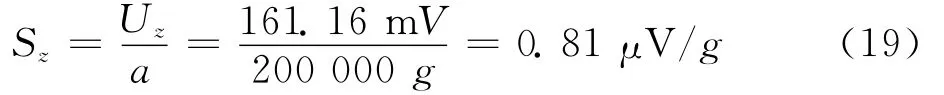
将X方向的差值代入式（17），求得输出电压为30.48 mV，则X方向的灵敏度为：

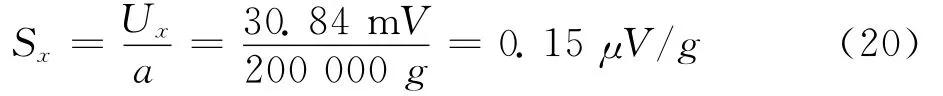
Y方向的灵敏度与X方向相同.

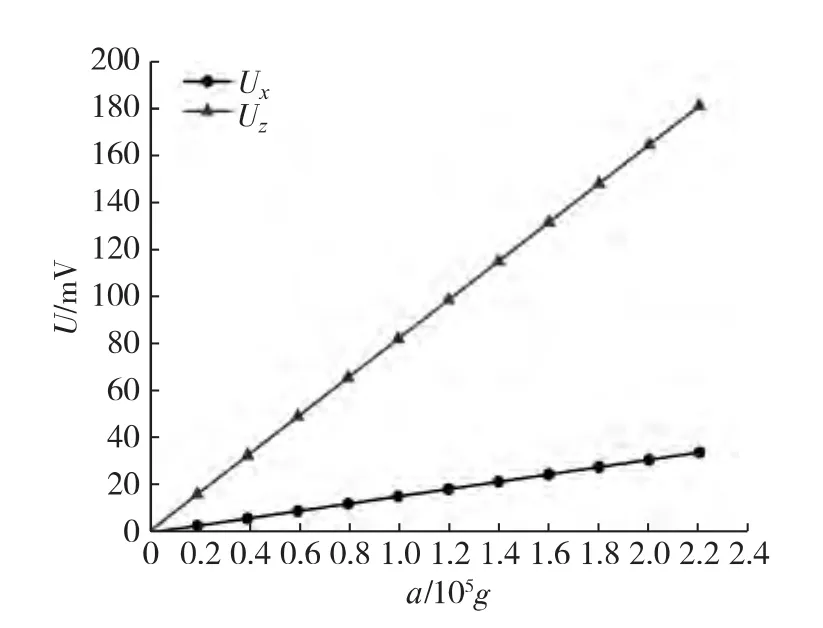
图10 三轴加速度和输出电压的关系Fig.10 Relationship between output voltage and acceleration in three axis

3.2 三轴的线性度

将应力表达式（9）分别代入输出电压的表达式（16）和（17），可提出一个公因子加速度a，故理论上输出电压与加速度成正比.通过仿真不同加速度的应力情况代入式（16）和（17），得到三轴的输出电压和a的关系如图10所示，由图可知输出电压在高g变化中保持线性.

4 结 论

通过理论推导和ANSYS分析设计了一种高g八梁压阻式微加速度计，在满足强度条件的情况下，通过应力和频率分析确定了梁的结构尺寸，接着分析得到了最适合布置电阻的位置，并仿真求解了三轴的灵敏度和线性度.本文提出了一种在明确的负载目标下和有限的空间中，分析设计性能优良的微加速度计的方法，所得结果对实际应用具有重要的指导意义.

［1］Robert B.MEMS sensors：past，present and future［J］.Sensor Review，2007，27（1）：7－13.

［2］Najafi K，Chac J，Kulah H，et al.Micromachined silicon accelerometers and gyroscopes［C］∥Intelligent Robots and Systems，2003IEEE／RSJ International Conference on.Las Vegas，USA：IEEE，2003：2353－2358.

［3］马喜宏，周鹏斌，李建军.高g值微加速度计在冲击环境下的可靠性［J］.测试技术学报，2010，24（5）：402－404.

［4］郭涛，鲍爱达.一种压阻式硅微复合量程加速度计［J］.弹箭与制导学报，2010，30（6）：186－189.

［5］孟美玉，刘俊，石云波.三轴压阻微加速度计的结构力学分析［J］.中国惯性技术学报，2007，15（3）：355－358.

［6］石云波，孟美玉，刘俊，等.基于SOI的三轴压阻微加速度计的设计［J］.传感技术学报，2008，21（3）：454－456.

［7］李平，石云波，朱正强，等.MEMS高g加速度传感器固有频率的优化及验证［J］.传感技术学报，2010，23（3）：388－392.

［8］Xiong J J，Fan B，Guo H G，et al.Calculation，simulation，and testing for the natural frequency of a micro accelerometer［J］.Journal of Semiconductors，2008，29（9）：1715－1722.

［9］梅年松，黄庆安.MEMS薄膜断裂强度测试结构［J］.微纳电子技术，2002，39（12）：32－35.

［10］Wilson C J，Ormeggi A，Narbutovskih M.Fracture testing of silicon microcantilever beams［J］.Journal of Applied Physics，1996，79（5）：2386－2393.