一种基于蚁群算法的用户浏览路径推荐方法

刘晋佩，曾建平

（厦门大学信息科学与技术学院，福建 厦门361005）

随着计算机技术和网络的迅速发展，互联网的信息量呈爆炸式增长，信息过载成为互联网发展所面临的主要挑战.尤其在电子商务领域，信息过载问题更加突出，推荐系统正是解决该问题的有效手段之一.在电子商务推荐系统中［1］，协同过滤算法是应用最为广泛的方法，它具有推荐效果好，实现和维护代价低等优点，成为最成功的个性化推荐技术之一.Xerox PARC研究中心提供的Tapestry［2］被认为是第1个协同过滤推荐系统，该系统用于过滤E－mail信息和Usent文章.由于协同过滤技术是基于用户对项目的评分数据，随着电子商务系统中用户和项目的快速增长，数据稀疏程度不断扩大，从而造成整个推荐系统的准确度不断降低.此外，推荐系统中新用户和新商品的加入还会造成系统无法完成推荐的冷启动问题.为了解决上述问题，需要探索新的推荐算法.

1 预备知识

Dorigo等［3］在1991年提出了蚁群算法，此后在他的其他著作中详细地阐述了该算法的基本原理和数学模型.蚁群算法是种群进化算法中的一种，具有良好的协作和搜索能力.同时还是一种本质并行的算法，能够迅速发现最优解.因此，蚁群算法非常适合应用于推荐系统中解决由数据集稀疏带来的问题.

根据蚁群算法［4］，一个完整的推荐系统可以看作是由蚂蚁所代表的用户以及蚂蚁所要寻找的“食物”所代表的商品项目构成，因此，有如下假设：

1）将用户看作是推荐系统中的蚂蚁，蚂蚁之间通过信息素进行交流；

2）将推荐系统中的目标商品项目看作蚂蚁要寻找的“食物”；

3）蚂蚁和食物之间存在很多非目标商品项目，将他们视为蚂蚁觅食路径上的节点，用户浏览这些商品项目就等同于蚂蚁访问这些节点，并留下信息素.这里信息素为用户对商品项目的评分.

设推荐系统中用户的总数为M，商品项目总数为N，记用户i对商品项目j的原始评分为a′ij，实时评分为a″ij，最终评分为aij.

用户间相似度的计算通常是利用用户对商品的评分信息来计算得到的［5］，其中Pearson相似性和余弦相似性是最常用的方法，由于Pearson相似性考虑了不同用户的评分喜好，因此可以提高寻找邻居用户的准确度，本文计算用户间的相似度所采用的便是Pearson相似性算法.定义用户i1和i2共同打过分的商品项目集合为Si1i2，则用户i1和i2之间的相似度sim（i1，i2）定义为：

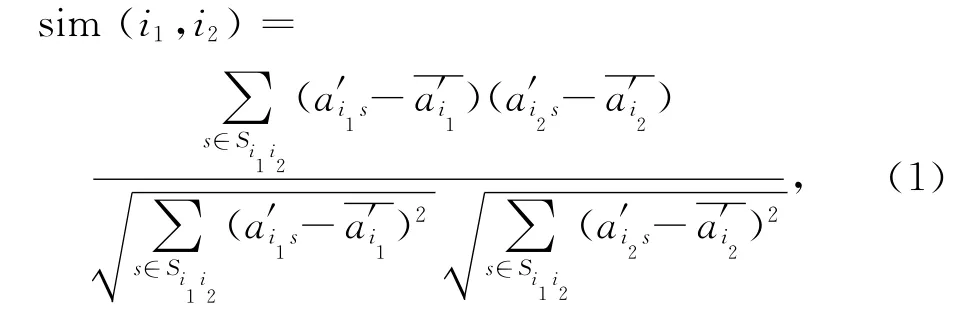
目标用户u的最近邻居集合用Su表示［6］，在Su中的用户是按与目标用户的相似度从高到低排列的，则目标用户u对未评分项目j的预测评分Puj为：

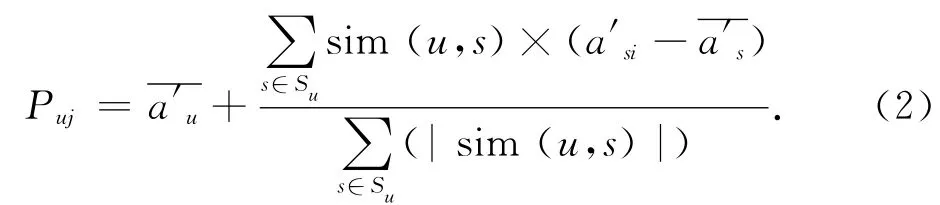
综上，用户i对项目j的最终评分［7］可表示为：

2 基于蚁群算法的推荐系统

2.1 转移概率函数的建立

用户在浏览商品时会根据浏览路径上信息素的强弱来决定下一个将要浏览的商品，这里用禁忌表集合tabu来记录用户浏览过的商品项目，集合D＝｛1，2，…，N｝为推荐系统中项目的集合，用户从项目j1转移到项目j2的转移概率为：

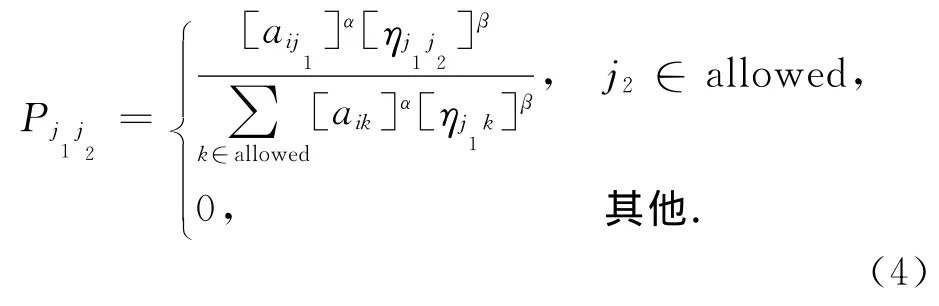
其中，allowed＝D－tabu表示用户下一步可选择的商品集，ηj1j2为能见度，它表示用户从项目j1转移到项目j2的期望程度，可根据某种启发式函数来确定，具体形式将在下文中给出.参数α和β分别表示信息素强度和能见度在转移概率中的相对重要性.α越大，表示用户更倾向于选择最近邻居集中用户选择过的商品.β越大，表示用户更倾向于选择与当前浏览项目相似的商品.

2.2 启发式函数的设计

启发式函数的设计来源于两部分，一部分来自于不同用户对同一项目的评分，为保持项目的原始属性，用项目j的原始评分向量Cj＝（a′1j，a′2j，…，a′Mj）来表示项目的评价属性值，项目j1和j2的相似性由余弦相似性公式来表示：

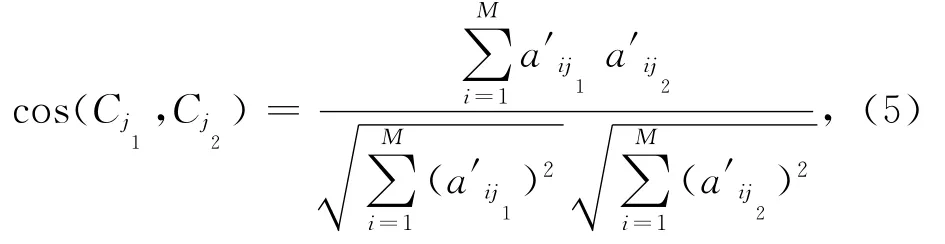
余弦值越大说明Ij1和Ij2越相似.

启发式函数的另一部分来自项目本身的属性值.设I为m个具有l维属性的项目数据集合I＝｛Ii｜Ii，i＝1，2，…，m｝，其中Iij指项目i的第j个属性值，则项目j1和j2间的相似度由欧氏距离公式来表示：

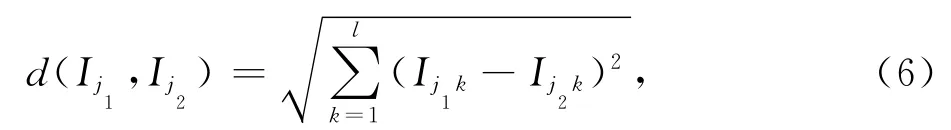
Ij1和Ij2的欧氏距离越小说明Ij1和Ij2越相似.

综上，启发式函数ηj1j2就可以表示为：

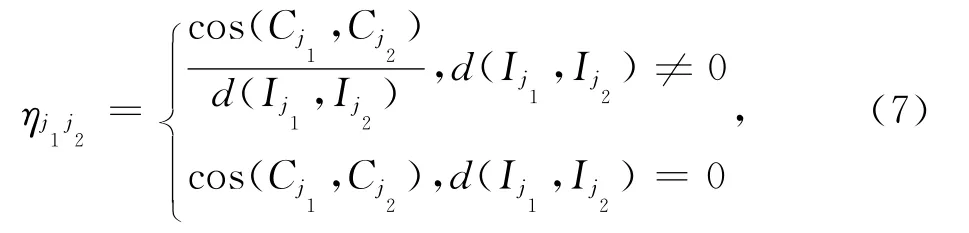
ηj1j2值越大，表明用户从项目j1转移到项目j2的期望程度越大，反之越小.

2.3 项目评分更新规则

蚂蚁在它行走的过程中会在其运动轨迹上留下信息素，信息素的强弱会影响到其他蚂蚁的行为，如果某条运动轨迹上的信息素越强，那么其他蚂蚁选择该轨迹的概率也就越大，当有蚂蚁从这条轨迹上经过时还会继续增加该轨迹上信息素的强度，当然，如果随后该轨迹上没有蚂蚁经过，信息素的强度就会逐渐减弱.这里信息素的更新实质上就是项目评分的更新，推荐系统每做一次推荐或遍历完所有的项目都会依据用户的反应，更新项目的评分，更新规则如下所示：

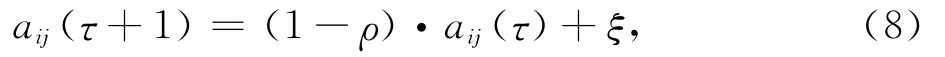
其中，ρ（0≤ρ＜1）表示信息素挥发因子，1－ρ为信息素残留因子，ξ为本次遍历过程中的信息素增量.

信息素残留因子表示不同蚂蚁间相互影响的关系［8］：当信息素残留因子过大时，之前搜索过的路径被再次搜索的可能性会增大，降低了算法的随机性和全局搜索能力；虽然通过减小信息素残留因子可以提高算法的随机性和全局搜索能力，但又会降低算法的收敛速度.ξ的初值为0，如果用户浏览并购买推荐项目时，会使项目评分增加，即ξ＞0；如果用户未浏览或浏览后未购买推荐项目时，ξ＝0.

3 实验结果与分析

3.1 数据集

实验采用由美国Minnesota大学的GroupLens研究小组创建并维护的MovieLens数据集，该数据集由943名用户对1 682部电影的100 000条评分记录所组成，其中，任一用户都至少对20部电影打过评分，评分范围是1～5，5表示“非常喜欢”，1表示“不喜欢”.评分的稀疏等级为ψ＝1－100 000／（943×1 682）＝0.93 695，可见，该数据集的评分矩阵是非常稀疏的.实验随机地把数据按8∶2的比例分为训练集和测试集，训练集用来产生实验结果，测试集用来测试实验结果的性能.

3.2 推荐质量的评价标准

这里采用分类准确度作为评价该算法优劣的标准［9］，分类准确度表示的是推荐系统能否正确预测用户是否喜欢某个商品的能力.网站在提供推荐服务时，一般给用户一个个性化推荐列表，长度为L.根据预测评分对训练集上的商品进行排序，记R（u）为用户u在训练集上的最可能喜欢商品列表，T（u）为用户u在测试集上的最喜欢商品列表，Tu为用户u在测试集上喜欢的商品数目，Npt为用户u在R（u）和T（u）上共有的商品数目.那么对用户u，其推荐结果的准确率Pu（L）（precision）和召回率Ru（L）（recall）分别表示为：

这里，Pu（L）表示系统所推荐的L个商品中用户真正喜欢的商品所占的比例，Ru（L）表示一个用户真正喜欢的商品能被推荐出来的概率.

3.3 实验结果分析

实验使用5对数据集进行测试，取5次实验的平均值作为实验的结果.实验中当取ρ＝0.3，ξ＝1.5，α＝1.8，β＝1.3时，取得较好的结果.为了验证本文提出的算法的有效性［10］，以ItemRank和 Maximum－frequency（MaxF）推荐算法作为对照，推荐长度从10增加到60，间隔为10，然后与本文提出的算法作比较，实验结果如表1所示.

将表1中的数据转换成图的形式，实验结果如图1所示.

由于MaxF算法只是将推荐系统内的项按被用户所浏览的次数进行简单的降序排序，将用户没有看过且排序靠前的项推荐给用户，没有考虑项目的评价属性和项目自身的属性，而ItemRank算法在将用户－项目评分二部图转换为相关图时会导致用户评分信息的丢失.本文提出的算法在运用蚁群算法强大的协作和搜索能力时，启发式函数的设计考虑了项目的评价属性和项目自身的属性，提高了寻找相似项目的准确度，同时保留了协同过滤算法来寻找目标用户的最近邻居集.从图1中可以看出，随着推荐长度的增加，3种算法的准确率均降低，召回率增加，但本文提出的算法不论准确率还是召回率都比MaxF和ItemRank算法有了明显提高，在推荐长度为40时本文提出的算法的准确率和召回率分别为27.14%和31.82%，比MaxF算法分别高出了10.82%和10.62%，比Item－Rank算法分别高出了9.91%和9.23%，证明了算法的有效性.

4 结 论

本文提出一种基于蚁群算法的电子商务推荐系统.该方法可有效地减少由数据集稀疏带来的问题，提高推荐系统的推荐质量，且通过设置相关参数解决新用户的冷启动问题.然而，蚁群算法中各参数的取值尚无严格的理论依据，至今还没有确定参数取值的一般方法，需要依靠大量的重复性实验寻找较优的结果.此外，由于推荐系统中的用户－评分矩阵是一个高维度的庞大矩阵［11］，且数据稀疏度极高，目前只能通过扫描评分矩阵来进行查询，并且蚁群算法的引入也提高了扫面时间的复杂度.因此，未来可以通过建立多维的动态索引结构，从而提高推荐系统的实时性.

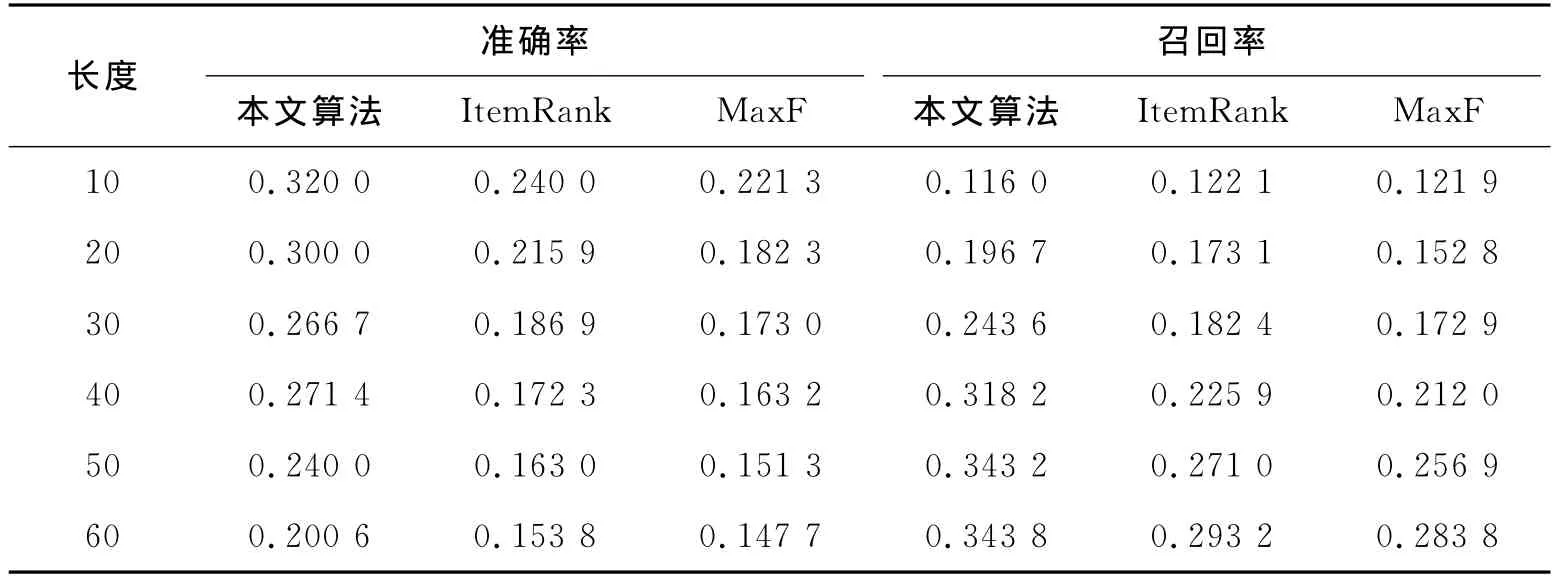
表1 不同推荐长度下各算法的准确率和召回率Tab.1 Precision and recall under the different length of recommended list

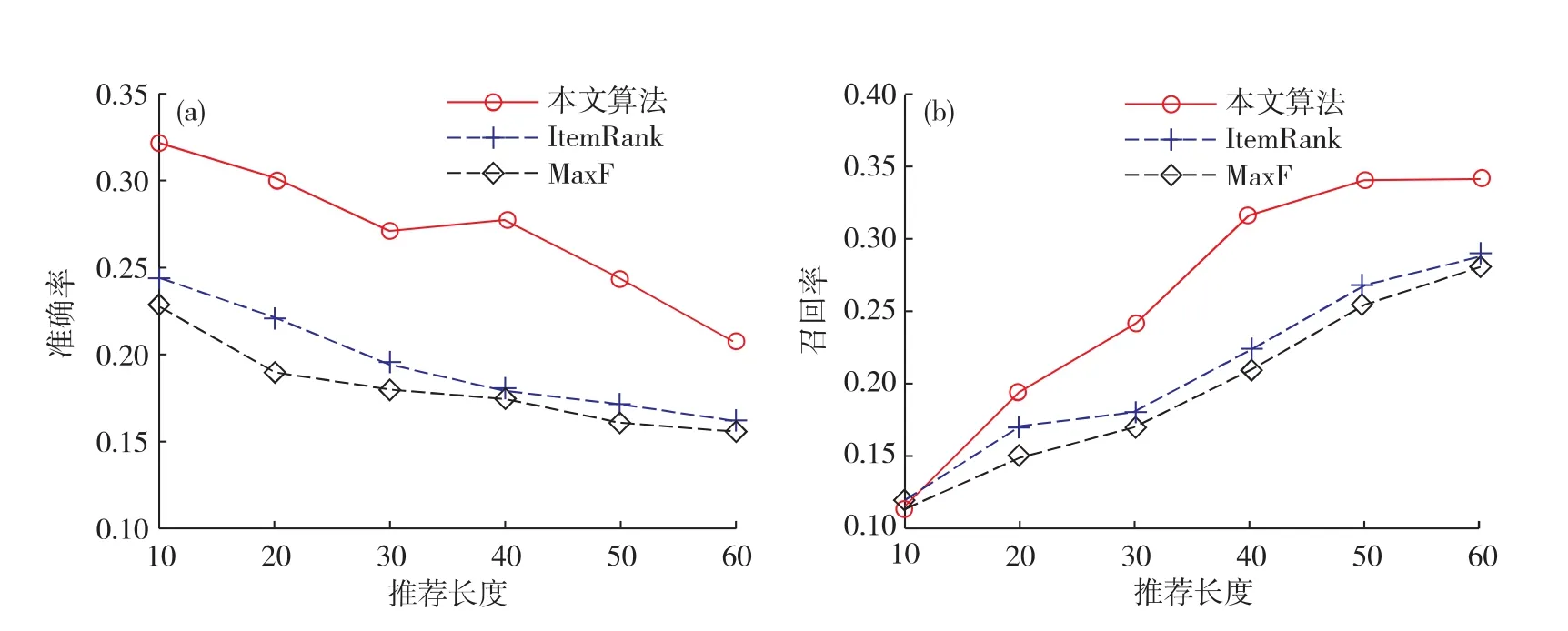
图1 3种算法在MovieLense数据集上的准确率（a）和召回率（b）Fig.1 Three algorithms performances of the MovieLens data set：（a）precision，（b）recall.

［1］Sarwar B，Karypis G，Konstan J，et al.Item－based collaborative filtering recommendation algorithms［C］∥Proceedings of the 10th International Conference on World Wide Web.New York，USA：ACM，2001：285－295.

［2］Deshpande M，Karypis G.Item－based top－N recommendation algorithms［J］.ACM Transactions on Information Systems（TOIS），2004，2（1）：143－177.

［3］Dorigo M，Maniezzo V，Colorni A.Ant system：optimization by a colony of cooperating agents［J］.Systems Man and Cybernetics，Part B：Cybernetics，1996，26（1）：29－41.

［4］王晗，夏自谦.基于蚁群算法和浏览路径的推荐算法研究［J］.中国科技信息，2009，33（7）：103－104.

［5］吴月萍，王娜，马良.基于蚁群算法的协同过滤推荐系统的研究［J］.计算机技术与发展，2010，21（10）：73－76.

［6］邓爱林，朱扬勇，施伯乐.基于项目评分预测的协同过滤推荐算法［J］.软件学报，2003，14（9）：1621－1628.

［7］周玉妮.基于蚁群算法的移动商务个性化推荐体系研究［D］.南京：南京邮电大学，2012.

［8］詹士昌，徐婕，吴俊.蚁群算法中有关参数的最优选择［J］.科技通报，2003，19（5）：381－386.

［9］朱郁筱，吕琳媛.推荐系统评价指标综述［J］.电子科技大学学报，2012，41（2）：163－175.

［10］Zhang Y，Wu J，Zhuang Y.Random walk models for top－N recommendation task［J］.Journal of Zhejiang University Science A，2009，10（7）：927－936.

［11］陈健，印鉴.基于影响集的协作过滤推荐算法［J］.软件学报，2007，18（7）：1685－1694.