柔性悬索吊桥的几何非线性特性

曹国辉，胡佳星，张锴，刘超

(1. 湖南城市学院 土木工程学院，湖南 益阳，413000；2. 湖南科技大学 土木工程学院，湖南 湘潭，411105)

柔性悬索吊桥与其他相同跨径的桥梁相比，结构简单，施工方便，造价低，在交通量不大和经济贫困地区的道路上经常使用[1]，但其刚度小，变形大，抗风能力差，不能承压，也不能抗弯，仅承受拉力作用，几何非线性特性突出[2]。在荷载作用下，柔性吊桥的主索几何形状和内力会发生变化，因此，正确分析荷载作用下主索的受力情况成为柔性吊桥设计的关键。而目前人们对悬索吊桥设计理论研究较多，而对大中型刚性桥型的研究较少，对于柔性吊桥则从理论到实践有不完善之处，且施工难以达到设计要求，甚至造成病害，严重时还造成桥毁人亡[3−7]。随着悬索吊桥的广泛修建，其结构计算理论不断发展和更新，国内外专家采用不同的方法对悬吊结构进行了线性或非线性理论分析[8−9]。目前，国内大多数研究者只对设计、施工等关键技术进行了理论探讨[10−11]，而对悬索吊桥成桥后荷载试验的研究较少，对主索在竖向荷载作用下效应及线形变化规律的研究更少。为此，本文作者对柔性悬索吊桥几何非线性特性进行分析。

1 工程概况

某人行桥设计荷载为人群荷载3.5 kN/m2。上部结构采用悬索结构，拉索锚固于桥台上，主索采用6根

GB/T 8918—96的钢芯Φ44 mm6×61的I级镀锌钢丝绳，抗拉强度为1.770 GPa；桥梁主跨为68 m，矢跨比为1/30，桥面净宽为1.8 m。在主索间共设置13道平衡梁，平衡梁为钢结构构件。下部结构采用承台及钻孔灌注桩基，桩径均为1.5 m。悬索吊桥结构简图见图1。

图1 悬索吊桥结构简图Fig. 1 Structure diagram of suspension bridge

2 空载下主索初始状态有限元分析

荷载试验前对主索线形进行测量，测试出主索实际垂度。主索线形测点布置见图 2，各测点主索控制截面实测垂度与设计垂度对比见图3。

由图3可知：跨中处实测垂度为−2.248 m，比设计跨中垂度高0.019 m，偏差为0.85%，且在空载下桥面几乎完全对称，施工控制较好，线形符合设计要求。

由于吊桥是柔性悬挂结构，允许变形大，线性系统的小位移假设不再适用，在几何方程和平衡方程中，必须考虑变形导致几何关系的改变，构成非线性大位移问题。吊桥的结构应力水平偏低，材料处于线弹性范围，属于小应变下的大位移问题，应按几何非线性问题处理[2]。

吊桥的计算主要采用3种理论：弹性理论、挠度理论以及有限位移理论[12−13]。本文利用大型有限元分析软件Midas对该悬索吊桥进行计算机仿真模拟，分析荷载作用下吊桥的受力性能，得出初始平衡状态下主缆的坐标和张力。该桥共有6根主索，为了避免复杂的桥型建模，提高设计计算精度与效率，采用单索模拟实际受力情况，将实测的主索垂度和相关参数导入有限元分析软件，可将结构划分为140个单元，经过计算可得到设计荷载相当于单索上每个节点(节点间距为0.5 m)承受竖向向下力0.53 kN。对模型进行有限元分析计算，可得到主索138个单元的初始内力(大位移)中的几何刚度初始荷载，荷载方向为轴向。同时，可以得到所有主索单元的初始内力(小位移)中的初始单元内力。单索模型结构受力见图4。

图4 单索模型结构受力图Fig. 4 Structure diagram of single line model

3 静力荷载试验

根据静力荷载试验规定要求，采用4级加载和2级卸载的方式对该桥进行荷载试验。静载试验采用水箱加载，水箱长为12.0 m，宽为1.5 m，加载位置为跨中。经有限元数值分析确定该静载试验需加载总重力为135.0 kN。水箱荷载分级见表1，桥面水箱布置区域见图5。

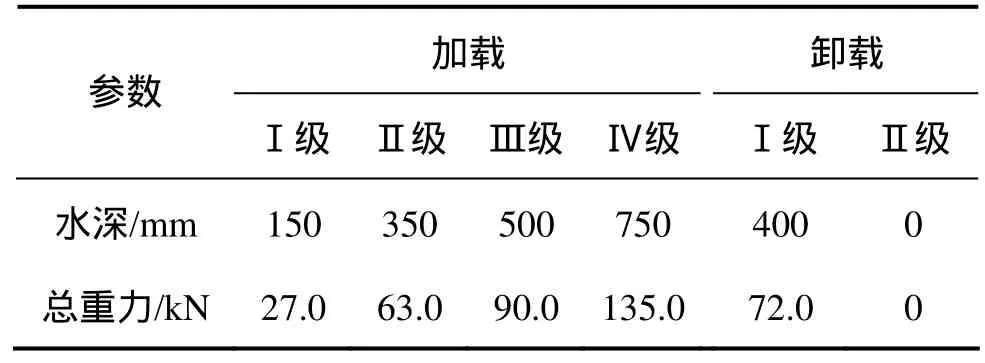
表1 加载分级表Table 1 Loading classification

图5 桥面加载区域布置Fig. 5 Loading area layout on bridge deck

对该桥L/8截面、L/4截面、3L/8截面、跨中截面、5L/8截面、3L/4截面、7L/8截面的变形进行观测，对该桥桥台水平位移进行测试，主索垂度及桥台水平位移测点布置见图6。

图6 主索垂度及桥台水平位移测点布置Fig. 6 Measuring point layout of main cable sag and abutment horizontal displacement

4 主索垂度测试结果

在静力荷载试验工况下，两桥台未见水平位移，各工况下主索垂度测试结果见表2。

表2 各工况下主索垂度实测值和仿真值对比Table 2 Comparison of measured horizontal displacements with simulation horizontal displacements of the main cable sag under various conditions mm

在静力荷载试验中，根据垂度测试结果，主索各测点垂度实测值均小于仿真值，相对残余变位最大为8.8%，符合JTG/T J21—2011(《公路桥梁承载能力检测评定规程》)[14]所规定的容许值 20%的要求，在加载过程中，桥台无水平位移。为了判断主索的受力性能，分析满载作用下实测垂度与仿真值偏差和在各个工况下主索垂度实测值的变化趋势，主索垂度变化曲线对比见图7。

由图7可知：在IV级荷载作用下主索测试截面的垂度实测绝对值较仿真值偏小，说明主索受力状态良好，整体质量达到了荷载等级设计要求；主索垂度的实测值与仿真值一致，说明本文有限元分析方法能模拟出悬索吊桥实际受力状态，对悬索吊桥受力性能评估具有较高可靠度。

图7 主索控制截面垂度变化曲线对比图Fig. 7 Comparison of horizontal displacement of main cable sag in control sections

5 主索几何非线性特性

5.1 主索垂度与竖向荷载的关系

为了研究主索垂度与荷载之间的关系，将各测试截面在每级荷载作用下荷载增量与实测垂度增量相比，求出控制截面增加单位垂度时需要的荷载，即以主索垂度变化量为横坐标，以荷载增量为纵坐标，斜率k为增加单位垂度时所需的荷载。八分点处截面斜率k见表3。

由表3可知：控制截面L/8和7L/8斜率变化最大，增加单位垂度的所需荷载量逐渐增大；斜率变化较大的是控制截面L/4和3L/4附近，增加单位垂度的所需荷载逐渐减少；在3L/8，5L/8和L/2截面附近，斜率变化幅度不大，增加单位垂度所需荷载的幅度波动很小。

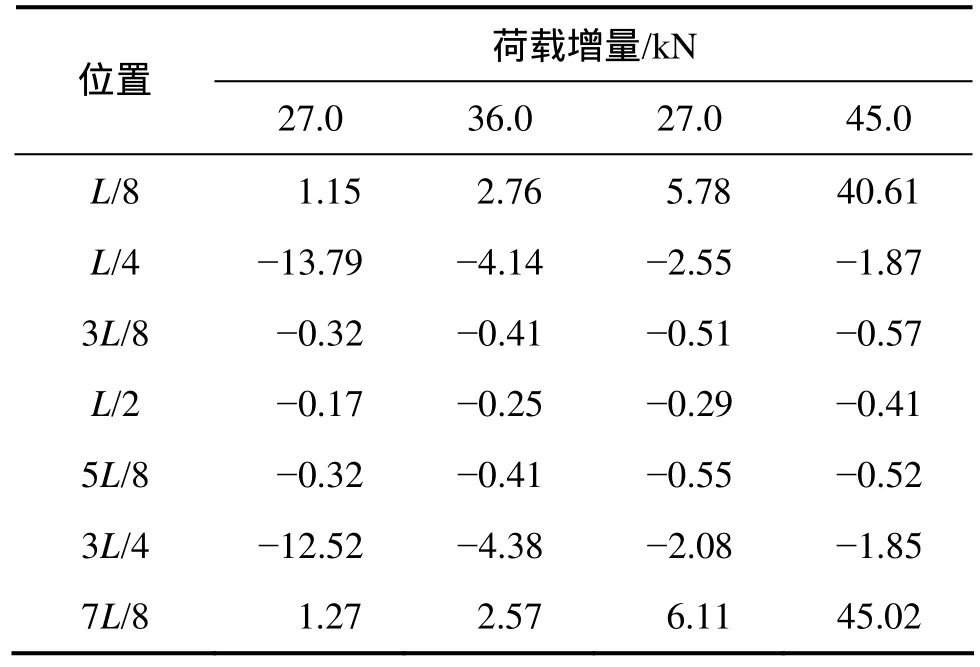
表3 不同竖向荷载下八分点处控制截面的斜率kTable 3 Eight points slope of control sections at different vertical loads

为了更好地对比主索各截面垂度与跨中竖向荷载之间的关系，在各个工况下，将主索各截面实测垂度随荷载的变化进行对比，见图 8。为了避免实测数据误差造成分析偏差，将各个工况下主索各截面仿真垂度随荷载的变化进行对比，见图9。

由图8和图9可知：实测主索垂度与仿真垂度变化趋势一致；从工况I到工况IV加载过程中，L/8和7L/8截面的2条线形斜率逐步减少，最后趋近于0，主索垂度逐渐收敛于60 mm；L/4和3L/4截面的2条线形斜率逐步增大；3L/8，5L/8和L/2截面的线形基本呈线性关系。

定义斜率比为控制截面中较大斜率除以较小斜率，即斜率比＞1，各控制截面斜率比区间见表4。

由表4可知：L/8和7L/8截面斜率比最大为35.44，L/4和3L/4截面斜率比最大为7.37；当主索从3L/8和5L/8截面向端部截面趋近时，主索几何非线性特性明显；从主索3L/8和5L/8截面向跨中截面趋近时，斜率比区间幅度不大，基本处于1.05～1.78，主索几何非线性特性不明显；从跨中截面向端部趋近过程中，主索几何非线性特性更加突出。

图8 各个工况下主索各截面实测垂度随载荷变化趋势Fig. 8 Variation trend of measured horizontal displacement of main cable sag with increasing loads under various conditions in each section

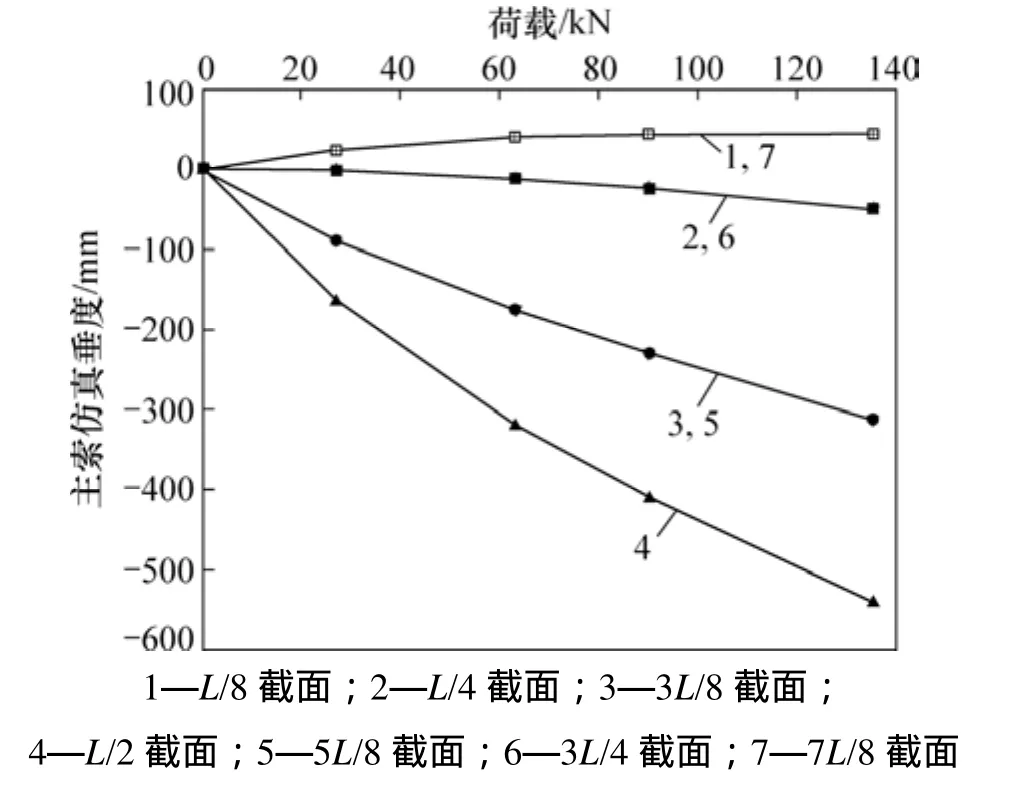
图9 各个工况下主索各截面仿真垂度随载荷变化趋势Fig. 9 Variation trend of simulation horizontal displacement of main cable sag with increasing loads under various conditions in each section

表4 不同竖向荷载下控制截面的斜率比区间Table 4 Slope ratio range of control sections at different vertical loads

5.2 主索垂度与轴向应力的关系

由上述分析可知，本文数值分析方法能模拟悬索吊桥实际受力状态，对桥梁受力性能评估具有可靠性，故有限元模型中主索轴向应力可以反映主索张力实际受力情况。定义此处斜率为增加单位垂度所需轴向张力，主索各控制截面轴向应力如表5所示，主索各截面在各个工况下八分点处截面的斜率见图10。

由表5可知：控制截面L/8和7L/8斜率变化最大，增加单位垂度的所需轴向应力逐渐增大；斜率变化较大的是控制截面L/4和3L/4附近，增加单位垂度的所需轴向应力逐渐减少；在3L/8，5L/8和L/2截面附近，斜率变化幅度不大，增加单位垂度所需轴向应力的幅度波动很小。

表5 不同轴向应力下八分点处控制截面的斜率kTable 5 Eight points slope of control sections at different axial stresses

图10 在各个工况下主索各控制截面实测垂度与轴向应力关系对比图Fig. 10 Relationship between measured horizontal displacement of main cable sag and axial stress under various conditions in each control section

由图10可知：从工况I到工况IV加载过程中，L/8和7L/8截面的2条线形斜率逐步减少，最后趋近于0，主索垂度逐渐收敛于60 mm；L/4和3L/4截面的两条线形斜率逐步增大；3L/8，5L/8和L/2截面的线形基本呈线性关系。各控制截面的斜率比区间见表6。

由表6可知：L/8和7L/8截面斜率比最大为39.95，L/4和3L/4截面斜率比最大为7.21；当主索从3L/8和5L/8截面向端部截面趋近时，主索几何非线性特性明显；从主索3L/8和5L/8截面向跨中截面趋近时，斜率比区间幅度较少，基本处于1.09～1.82，主索几何非线性特性不明显；从跨中截面向端部趋近过程中，主索几何非线性特性更加突出。

表6 不同轴向应力下控制截面的斜率比区间Table 6 Slope ratio range of control sections at different axial stresses

6 结论

(1) 柔性悬索吊桥受力性能良好，整体质量能够满足荷载等级设计要求，试验挠度与有限元仿真结果接近，说明本文有限元分析方法能模拟出悬索吊桥实际受力状态，对桥梁受力性能评估具有可靠性，相关结论可为柔性吊桥悬索系统的设计提供依据。

(2) 从主索3L/8和5L/8截面向跨中截面趋近时，几何非线形特性不明显，主索垂度增量与跨中所加荷载增量和轴向张力基本呈线性关系；从主索 3L/8和5L/8截面向端部截面趋近时，几何非线性特性更加明显。

(3) 在L/4和3L/4截面附近，主索增加单位垂度所需荷载量和轴向张力逐渐减少；在L/8和7L/8截面附近，主索增加单位垂度所需荷载量和轴向张力逐渐增大；在L/2，3L/8和5L/8截面附近，主索增加单位垂度所需荷载量和轴向张力相差很小。

[1]黄辉. 山区柔性吊桥主缆线形计算方法研究与应用[J]. 公路工程, 2010, 35(4): 94−96.HUANG Hui. Research and application on calculation methods for cable curve of flexible suspension bridge in mountain road[J].Highway Engineering, 2010, 35(4): 94−96.

[2]吴忠华, 付晓墩, 向中富, 等. 关于影响单跨吊桥刚度因素的讨论[J]. 公路交通技术, 2005(3): 100−103.WU Zhonghua, FU Xiaodun, XIANG Zhongfu, et al. Discussion on influencing factors of single span suspension bridges[J].Technology of Highway and Transport, 2005(3): 100−103.

[3]郑丽凤, 周新年, 黎宗禄, 等. 柔性吊桥设计理论及其应用研究 IV: 柔性吊桥悬索系统设计数学模型[J]. 东北林业大学学报, 2005, 33(1): 49−51.ZHENG Lifeng, ZHOU Xinnian, LI Zonglu, et al. Design theory and applied study on a flexible suspension bridge IV:Mathematical models for the cable system design of flexible suspension bridge[J]. Journal of Northeast Forestry University,2005, 33(1): 49−51.

[4]官印生, 周新年, 郑丽凤, 等. 柔性吊桥设计理论及其应用研究 VII:基于 VB的柔性吊桥悬索设计系统[J]. 东北林业大学学报, 2006, 34(2): 73−75.GUAN Yinsheng, ZHOU Xinnian, ZHENG Lifeng, et al. Design theory and applied study on flexible suspension bridges (VII): A VB-based designing system for cable of flexible suspension bridge[J]. Journal of Northeast Forestry University, 2006, 34(2):73−75.

[5]周孟波. 悬索桥手册[M]. 北京: 人民交通出版社, 2003: 6−12.ZHOU Mengbo. Handbook of suspension bridges[M]. Beijing:People’s Transportation Press, 2003: 6−12.

[6]向中富. 桥梁施工控制技术[M]. 北京: 人民交通出版社,2001: 1−14.XIANG Zhongfu. Construction control technology of bridge[M].Beijing: People’s Transportation Press, 2001: 1−14.

[7]周昌栋, 谭永高, 宋官保. 悬索桥上部结构施工[M]. 北京:人民交通出版社, 2004: 2−6.ZHOU Changdong, TAN Yonggao, SONG Guanbao.Superstructure construction of suspension bridges[M]. Beijing:People’s Transportation Press, 2004: 2−6.

[8]张翔, 贺栓海, 李江山. 双索面悬索吊桥的静力数值分析[J].华东公路, 1990(3): 52−57.ZHAGN Xiang, HE Shuanhai, LI Jiangshan. Static numerical analysis of flexible suspension bridges with double cable planes[J]. East China Highway, 1990(3): 52−57.

[9]唐建民, 沈祖炎. 悬索结构非线性分析的滑移索单元法[J].计算力学学报, 1999, 16(2): 143−148.TANG Jianmin, SHEN Zuyan. A nonlinear analysis method with sliding cable elements for the cable structures[J]. Chinese Journal of Computational Mechanics, 1999, 16(2): 143−148.

[10]钱炜, 刘鹏. 柔性悬索桥动力特性分析[J]. 浙江水利水电专科学校学报, 2009, 21(2): 89−92.QIAN Wei, LIU Peng. Research on dynamic characteristic of flexible suspension bridges[J]. Journal of Zhejiang Water Conservancy and Hydropower College, 2009, 21(2): 89−92.

[11]董明. 柔性吊桥悬索的几何非线性计算方法[J]. 云南工学院学报, 1993, 9(1): 23−29.DONG Ming. Calculation method about geometrical non-linear characteristic of flexible suspension bridges[J]. Journal of Yunnan Institute of Technology, 1993, 9(1): 23−29.

[12]铁道部大桥工程局桥梁科学研究所. 悬索桥[M]. 北京: 科学技术文献出版社, 1996: 24−69.Bridge scientific research institute of major bridge engineering bureau of ministry of railways. Suspension bridge[M]. Beijing:Science and Technology Literature Press, 1996: 24−69.

[13]钱冬生, 陈仁福. 大跨悬索桥的设计与施工[M]. 成都: 西南交通大学出版社, 1992: 6−13.QIAN Dongsheng, CHEN Renfu. The design and construction of large span suspension bridge[M]. Chengdu: Southwest Jiao Tong University Press, 1992: 6−13.

[14]JTG/T J21—2011, 公路桥梁承载能力评定规程[S].JTG/T J21—2011, Specification for inspection and evaluation of load-bearing capacity of highway bridges[S].