基于灰色模型的集装箱货量预测
2014-11-30郑刚
郑 刚
(大连中远国际货运有限公司,辽宁 大连 116001)
基于灰色模型的集装箱货量预测
郑 刚
(大连中远国际货运有限公司,辽宁 大连 116001)
为提高集装箱货量的预算精度,根据灰色模型理论,建立基于GM(1,1)模型的集装箱货量预测方案,并首次将该模型运用到班轮公司集装箱货量的预测研究中。通过对中国远洋和中海集运2008—2011年的集装箱货量进行实证检验,证明GM(1,1)模型预测效果较好,对班轮公司宏观战略的制定和全面预算的管理具有重要意义。
交通运输经济学;预测;灰色模型;GM(1,1);集装箱量
2013年,世界经济危机与希望并存,全球集装箱班轮业继续挣扎在亏损与盈利的边缘。集装箱货运量是班轮公司最重要的经营数据之一,直接关系到主营业务的收入和成本,班轮公司发展战略的制定和全面预算的管理离不开对集装箱货量的科学预测。但是,在全球政治经济环境、市场竞争环境、运力投放、航线调整等诸多不确定因素的影响下,传统的线性回归模型已不再适用于集装箱货量预测,需寻找更加科学、合理的预测模型。
华中科技大学邓聚龙[1]教授创建的灰色模型理论适用于样本空间小、信息资源复杂的不确定性系统的研究。已有多位学者[2-11]将该模型应用于港口吞吐量的预测工作中,并取得了很好的成绩。本文通过实证检验,证明灰色模型在班轮公司集装箱货量的预测研究中同样具有较高的精度和实用价值。
1 灰色模型理论简析
1.1灰色模型的思想
基于灰色模型(Grey Model,GM)的预测方法称为灰色预测。传统的预测方法要求数据样本量大、数据遵循一定的变化趋势,而灰色预测对数据没有特殊要求,应用范围比较广泛。当时间序列无明显变化趋势时,采用累加的方法可生成一个变化趋势明显的时间序列,按该数列的增长趋势可建立预测模型,考虑灰色因子的影响进行预测,然后采用“累减”的方法进行逆运算,恢复原时间序列,得到预测结果。
1.2灰色模型的构建
目前使用比较广泛的灰色预测模型是关于数列预测的一个变量、一阶微分的GM(1, 1)模型。GM(1, 1)的构造如下。
设X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),其中,x(0)(k)≥0,k=1,2,…,n;X(1)为X(0)的一次累加生成序列:X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),其中
(1)
Z(1)为X(1)的紧邻均值生成序列:Z=(z(1)(2),z(1)(3),…,z(1)(n)), 其中

k=2,3,…,n
(2)
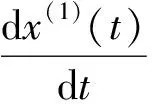
设待估参数列为P=[a,b]T,采用最小二乘法确定模型参数:P=(BTB)-1BTY
(3)
(4)
将式(4)代入式(3),并解微分方程,可得白化方程的解为
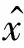
k=1,2,…,n
(5)
预测模型计算所得的结果为一次累加生成值的预测值,需对其进行一次累减还原才能得到原始值的预测值。
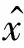
(6)
1.3灰色模型的检验
灰色理论建模可采用3种检验方式,即残差检验、关联度检验和后验差检验。残差检验是按点检验的,属于算术检验;关联度检验是根据模型曲线与行为数据曲线的几何相似程度进行检验的,属于几何检验;后验差检验是按照残差的概率分布进行检验的,属于统计检验。
1.3.1残差


(7)
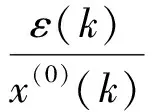
(8)
1.3.2关联度
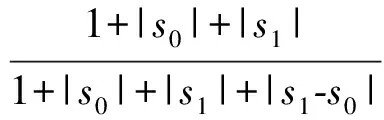
(9)




1.3.3后验差

(10)

(11)
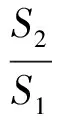
如果模型能够通过残差检验、关联度检验和后验差检验,则可用所建模型进行预测;否则,需要对模型进行残差修正。模型精度检验等级见表1。
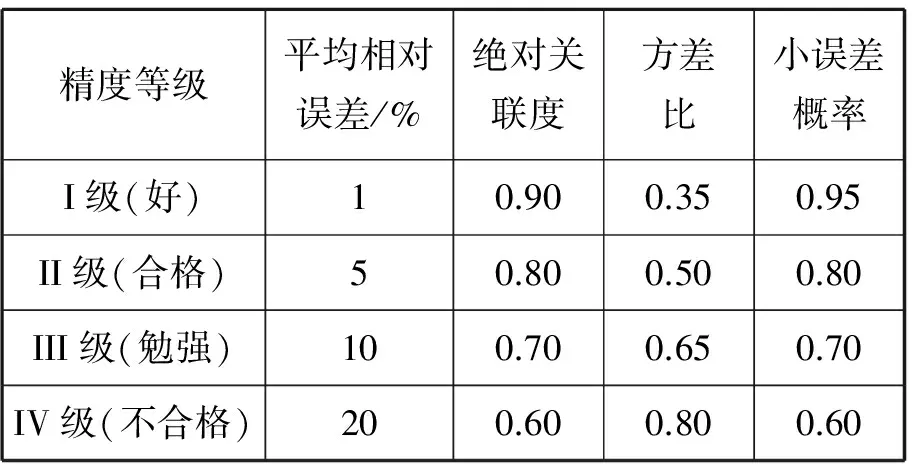
表1 模型精度检验等级
2 基于GM(1,1)的集装箱货量预测
2.1样本数据
根据中国远洋(SH.601919)近年公布的集装箱货运量数字,利用GM(1,1)模型对2012年该公司集装箱货运量进行预算,样本数据序列见表2。

表2 2008—2011年中国远洋集装箱货运量 TEU
2.2模型建立
按照表2的数据,构造原始时间序列:
X(0)=(5 792 593,5 234 292,6 215 371,6 910 041)
一次累积生成序列:
X(1)=(5 792 593,11 026 885,17 242 256,
24 152 297)
紧邻均值生成序列:
Z(1)=(8 409 739,14 134 570.5,20 697 276.5)
可知
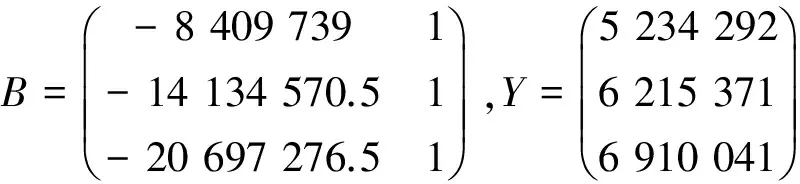
利用最小二乘法求得参数列
建立中国远洋集装箱货运量预测模型为
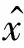
(5 792 593+30 705 541)e0.135 638k-30 705 541
2.3模型预测及精度检验
依据创建模型预测集装箱货运箱量,并计算绝对误差和相对误差(见表3)。
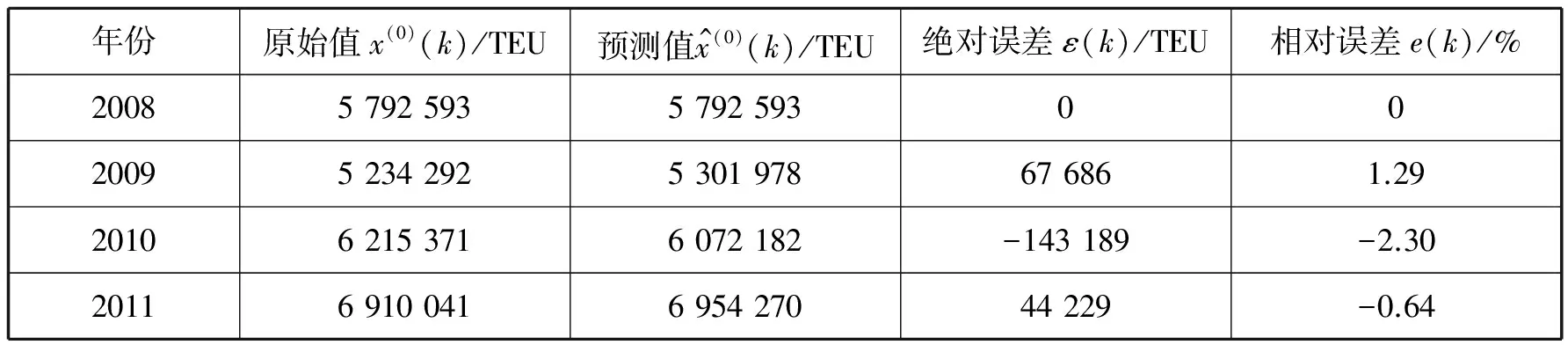
表3 2008—2011年中国远洋集装箱货运量预测值及误差
1) 残差检验:平均相对误差为1.412 336%,预测误差比较小。
2) 关联度检验:绝对关联度为0.936 9gt;0.90,原始序列于预测序列关联度很高。
3) 后验差检验:方差比C=0.137lt;0.35,小概率误差P=1gt;0.95。
因此,判定模型等级为I级,不需要对模型进行修正,模型预测精度高。
利用上述GM(1,1)模型,对2012—2015年中国远洋集装箱货运量进行预测(见表4)。

表4 2012—2015年中国远洋集装箱货运量预测 TEU
预测2012年中国远洋集装箱货运箱量可达796.4万TEU,2013年将达到912万TEU。
2.4对中海集运(SH.601866)的集装箱货量预测
参照上述方法,对国内第二大集装箱班轮公司中海集运(SH.601866)建立GM(1,1)模型为

(6 942 148+129 441 927)e0.048 59k-129 441 927
该模型等级也为I级,预测结果见表5。

表5 2012—2015年中海集运集装箱货运量预测 TEU
预测2012年中海集运的集装箱货运量可达784.8万TEU,2013年将达到823.9万TEU。
2.5实证检验
根据中国远洋和中海集运公布的2012年年报,实际货运量和预测的误差见表6。
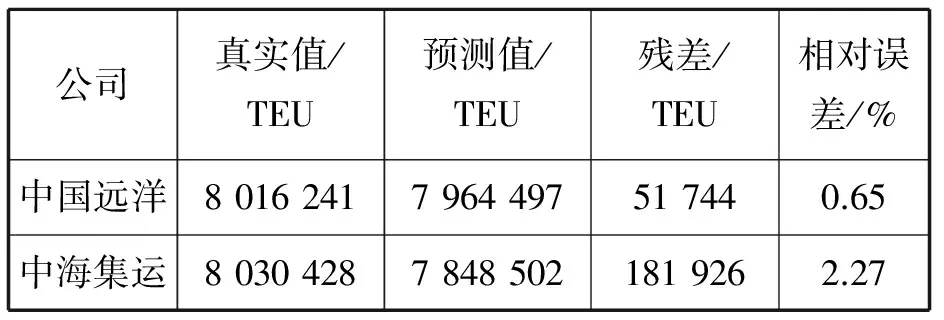
表6 2012年预测箱量和实际箱量
2012年初,中国远洋自身预测当年货量730万TEU,而实际完成801.6万TEU。显然,灰色模型预测结果误差很小,精度很高,具有较高的实用价值。
4 结 语
GM(1,1)模型具有无限增长的特性,即当时间无穷大时所得的预测结果也将趋向于无穷大。因此,灰色模型在集装箱货量的短期预测中是适用的,而中长期预测的结果的可靠性就明显偏弱,所以一般只选取前两个预测数据值。
即便如此,通过上述实证研究,证明灰色模型可以成功地预测集装箱货量,对班轮公司战略制定和全面预算工作具有重要意义,值得借鉴、推广。
[1] 邓聚龙.灰理论控制[M].武汉:华中理工大学出版社,2002.
[2] 曾波,孟伟.面向特殊序列的灰色预测建模方法[M].重庆:重庆大学出版社,2011.
[3] 党耀国,刘思峰,王正新,等.灰色预测与决策模型研究[M].北京:科学出版社,2009.
[4] 欧阳凯,袁松宝,刘俐.基于灰色模型的我国物流产业增加值预测[J].物流工程与管理, 2011,33(11):61-63.
[5] 陈淑燕,陈家胜.一种改进的灰色模型在交通量预测中的应用[J].公路交通科技,2004,21(2):80-83.
[6] 周茵.残差灰色预测模型在物流需求预测中的应用[J].铁道运输与经济,2007(11):59-61.
[7] 杨中庆,赵彬彬,廖慧敏.灰色组合模型在港口集装箱吞吐量预测中的应用[J].水运工程, 2006(9):14-15.
[8] 施泽军,李凯.基于灰色模型和指数平滑法的集装箱吞吐量预测[J]. 重庆交通大学学报:自然科学版, 2008,27(2):302-304.
[9] 钟霞,吴中,王丽.灰色理论及其组合模型在交通运量预测中的运用[J].交通标准化,2004(12):36-39.
[10] 万轶凌,朱士东.组合预测在水路货运量预测中的应用[J].交通与运输,2006(2):27-29.
[11] 虞亚平,王冠中,李大治.广义灰色关联度的简便计算方法[J].南通大学学报:自然科学版,2008,7(2):85-90.
GreyModelforPredictionofContainerShipment
ZHENGGang
(Dalian International Freight Co., Ltd, Dalian 116001, China)
The study was designed to predict the quantity of container shipment. The method used in this study is gray system model GM(1,1). With shipping data between 2008 and 2012, the prediction technology is used to forecast the container shipment of COSCON and CSCL. Test results indicate that GM(1,1) model is of higher adaptability and accuracy.The research is of great value to the managment of shiping company.
prediction; gray mode; GM(1,1); container shipment
2014-01-10
郑 刚(1974-),男,山东肥城人,工程师,硕士生,从事集装箱管理及市场预测研究。E-mail: zhg@sanly.cn.
1000-4653(2014)02-0118-04
F552
A
