水上交通流结构复杂度建模

文元桥， 黄亚敏， 杨君兰， 肖长诗，2， 周春辉，2， 吴晓春，2

(1.武汉理工大学 航运学院，武汉 430063； 2.湖北省内河航运技术重点实验室，武汉 430063)

水上交通流结构复杂度建模

文元桥1,2， 黄亚敏1， 杨君兰1， 肖长诗1，2， 周春辉1，2， 吴晓春1，2

(1.武汉理工大学 航运学院，武汉 430063； 2.湖北省内河航运技术重点实验室，武汉 430063)

为定量研究局部水域交通流的复杂性，通过解析水上交通流的结构特征，建立一种水上交通流复杂性测度模型。该模型由交通密度因子和交通冲突因子组成，不仅能够有效地反映出船舶之间的相对距离、航迹交叉角和相对速度对水域交通流复杂性的影响，还能揭示所研究水域的交通流复杂度的空间分布规律。以深圳西部海域的水上交通流为例，建立了该海域的水上交通流复杂度模型。经过实例验证，证明了该模型能够客观地反映出水域交通状态的变化特征。

水路运输；交通流；交通结构；复杂度建模；空间分布

近年来，水上交通流密度快速增加、船舶更加复杂和大型化等，客观上进一步增加了水上交通管理的难度。科学正确地认识管理和控制对象是实现有效管理和控制的前提，运用水上交通流理论，加深对水上交通流的认识，提高水上交通流管理效率已成为水上交通流管理研究的热点。目前，在水上交通流领域对交通流的研究可分为交通流外在特征研究和内部机理研究两方面。

1.在交通流外在特征方面，主要的研究方法是：根据交通流的历史数据或仿真数据，对交通流的特征进行归纳。如文献[1-2]重点分析交通流的特征，在统计交通流、预测交通流量和衡量交通流系统服务水平等方面取得了一定进展。然而,这类研究忽略了交通流内部船舶之间是实时地相互作用的，无法全面地描述交通流特征。

2.在交通流内部机理的研究方面，主要的研究方法有：基于流体动力学的交通流研究和基于动力学理论的交通流研究，如文献[3-4]。这类研究在船舶集体行为、航道通过能力及航道设计规划方面的研究中应用广泛,但忽视了船舶之间的联系。例如：将船舶交通流抽象为流体，但没有考虑单船之间的关系；或提出了船舶领域，但忽视了船舶领域之外船舶之间的联系。

通过上述分析可以发现，目前应用水上交通流理论对水上交通流系统的复杂性、非线性进行定量刻画存在不足。因此，引入水上交通复杂度的概念，运用复杂度理论研究基于微观交通关系的水上交通流的复杂性。

复杂性科学主要用于揭示复杂系统中一些难以用现有科学方法解释的动力学行为，目前已在经济、公路交通、航空交通和城市规划等领域中被广泛应用。[5]在交通领域，其主要的研究方向有：

1.动态密度(Dynamic Density，DD)。研究者认为动态密度是一类难以直接观测的多维复杂性测度指标，其数值的变化是引起复杂度生变化的根本原因。他们通常会选择交通密度、飞行状态、飞机机型和交通结构等易获取的交通参数作为模型的因子；再根据空域的不同特征，选择线性或非线性的函数关系构造动态密度。[6-8]

2.交通无序性研究。研究者认为交通复杂性只与交通流内禀属性有关。[9]

在航空领域，DELAHAYE等[10-11]提出利用交通的内禀属性(速度、航向和位置等)建立交通流复杂度的多维指标，在此基础上进一步提出了一类新的集合无序度量标准；LEE[9]以区域交通流为研究对象，分析了入侵航空器对区域交通复杂态势的影响。在国内，ZHANG等[12]在几何交通无序性研究的基础上建立基于交通流耦合关系的空域复杂性模型；叶博嘉等[13]建立的基于交通结构的复杂度模型能够反映空中交通流的几何特性对交通复杂性的影响。

在道路交通领域，研究者以断面时序数据为研究对象，利用近似熵或CD复杂度等方法，定量地衡量交通的复杂程度。[14-15]

从以上研究可以看出，复杂度作为交通流系统的重要刻画指标，已在道路交通和航空领域得到广泛应用。综上，在水上交通领域开展交通流复杂度研究及应用具有重要意义。

本文运用交通无序性研究方法研究水上交通流复杂度；以保障水上交通安全为目的，通过对港口水域水上交通结构进行解析，提出交通密度和交通冲突两类复杂度因子，构建水上交通流复杂度模型，以得到港口水域水上交通流复杂度的空间分布。

1 水上交通流复杂度建模条件

水上交通流复杂度与研究水域船舶交通流的特征密切相关。在宏观层面，交通流的特征体现在该水域内船舶交通流密度(即船舶的数量)上；在微观层面，交通流的特征体现在船舶间的几何关系上。因此,从船舶交通流密度和船舶间几何关系两方面研究港口水域交通流复杂度。

两艘船舶i和j构成了最基本的交通关系单元，记为VCij(Vessel Couple)。微观的交通关系单元决定了该水域整体的交通模式。在确定微观交通关系单元交通复杂性时，应遵循以下假设：

1.在研究每个交通关系单元时，必须满足该单元的交通复杂度连续性假设,即交通复杂度影响因素的变化将引起交通复杂度的连续变化,并且设该复杂度的下界为零，上界趋于无穷大。

2.为简化模型，选用70 000载重吨的散货船作为标准船型，船长(L)为230 m，型宽(B)为32.3 m。[16]

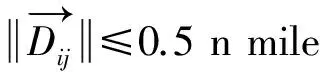
2 水上交通复杂度模型

2.1交通密度影响因子

研究水域的交通复杂度与该水域船舶的交通密度紧密相关,因此水域交通复杂性发生变化的一个重要原因是该水域的船舶密度增加了。

定义1：由交通密度直接引起的交通复杂度称为第Ⅰ类复杂性denij。

用单位水域内船舶数量表示的交通密度并不能完全表达出单位水域船舶的复杂程度。图1(a)与图1(b)中的船舶数量相同，但是图(b)中船舶间的间距较小，因此认为其交通密度较大，交通结构更为复杂。

(a)

(b)

(1)

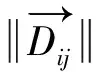
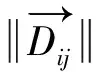
2.2交通冲突影响因子

定义3：由交通关系单元的交通态势引起的交通复杂性所建立的第Ⅱ类复杂性因子，称为冲突因子conij。

当船舶以相同的航速航行时，船舶间的冲突与船舶间的航迹交角和船舶的运动性能有关。[18]当船舶航迹交叉角相等时，船舶的运动趋势(相聚或相离)对船舶是否存在交通冲突也直接相关。因此，影响交通冲突因子的因素主要有：航迹交叉角因素和船舶运动趋势因素。

综上，冲突因子conij函数可表示为

(2)

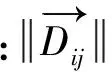
2.2.1航迹交叉角因素

在船舶领域，局部交通态势的复杂性影响并非随着航迹交叉角θ(见图2～图3)沿0°～180°单调变化，其变化范围为

(1) 当θ∈(0°,67.5°)时，根据《国际海上避碰规则》(下简称“规则”)船舶的会遇态势明确，属于船舶间的追越，前船与后船避碰的责任和义务明确，交通态势相对简单。追越船应给被追越船让路;

图2 航迹交叉角

图3 船舶会遇局面示意图

(2) 当θ=67.5°时，根据规则，划分船舶大角度交叉和追越关系的临界角为67.5°，当两船航迹交叉角在此角度时，船舶的会遇态势不易判断，并且在大角度交叉和追越情况下两船的责任和义务有明显不同，交通态势判断错误易造成严重后果;

(3) 当θ∈(67.5°,90°]时，根据规则，船舶的会遇态势明确，属于船舶间的大角度交叉，船舶间的责任义务明确，交通态势相对简单。让路船应给直航船让路;

(4) 当θ∈2(90°,174°]时，根据规则，船舶会遇态势明确，属于小角度交叉，船舶间的责任义务明确。当船舶速度大小相同时，由于船舶间的相对速度与船舶航迹交叉角θ成正比，随着θ的增加，交通态势逐渐复杂;

(5) 当θ∈(174°,180°]时，根据规则，船舶会遇态势属于对遇，两船舶的责任与义务相同，但是由于小角度交叉和对遇不易判断，并且船舶间的相对速度达到最大，交通态势的复杂性也相对较大。

据此，可构造由航迹交叉角引起的冲突因子复杂性(angleij)，见图4。

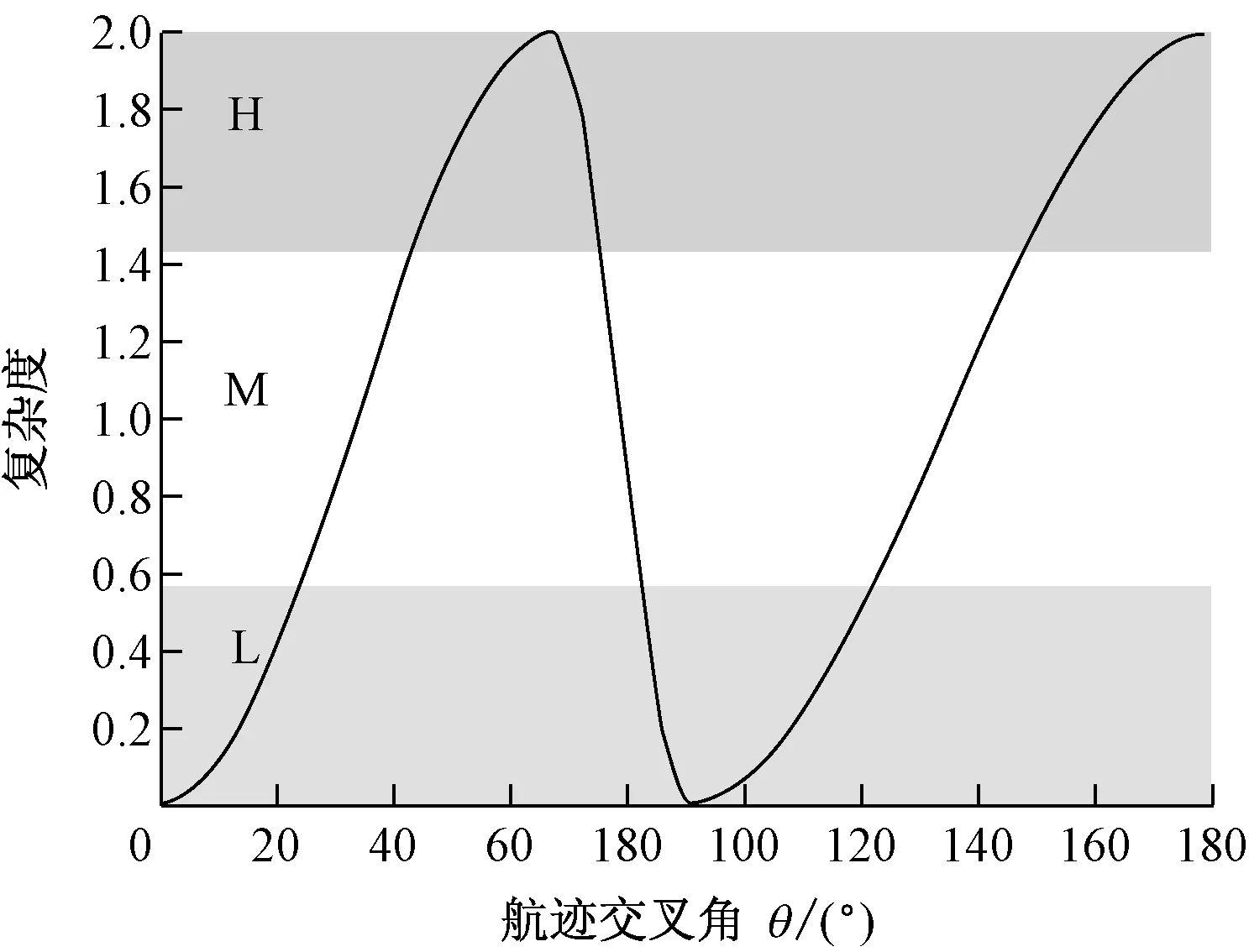
图4 不同航迹交叉角下的复杂度

由假设1可知，复杂性随距离减小而非线性地连续增大；由假设3，两船相距超过3 n mile无碰撞危险，认为船舶的潜在冲突很小，复杂性为极小值；由假设4，两船相距0.5 n mile以内时，船舶面临紧迫危险，相应的具有较高的管制紧迫性，复杂度视为极大值。

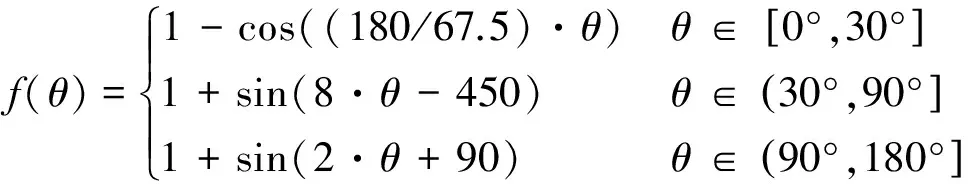
(3)

其图形见图5，复杂度在航迹交叉角θ=67.5°时取到最大值，在θ=90°时取到最小值，在θ∈(90°～180°)时非线性递增。

下第Ⅱ类较复杂度

下第Ⅱ类较复杂度

所以有冲突因子复杂性公式

(4)

为保证复杂度在区间内连续的假设，因此有

(5)

(6)

即

(7)

2.2.2运动趋势因素

交通关系单元内的船舶的相对运动趋势对船舶的冲突也产生重要影响。图6中，当船舶的航迹交叉角相同，而船舶的运动趋势不同时：图6(a)中的两船相互聚合；图6(b)中的两船相离。两种态势的冲突概率不同，因此需要考虑交通单元中两船的运动趋势，修正冲突复杂性。

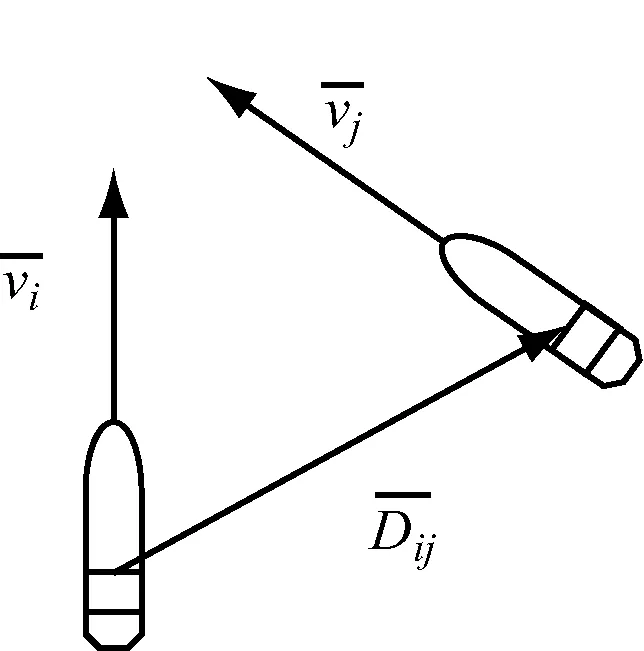
(a)

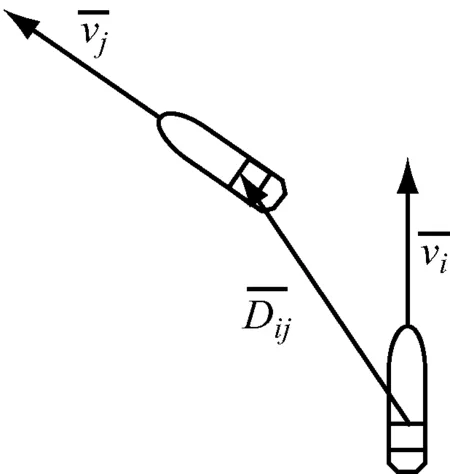
(b)

定义由船舶的相对运动趋势引起的冲突因子复杂性为Convij。若船舶有相离的趋势,则Convij=0;若船舶有相聚的趋势，则Convij与船舶的接近速度正相关。

设交通单元船舶相对速度为

(8)

则船舶相互接近的趋势为

(9)

(10)

根据航迹交叉角和相对运动趋势引起的交通冲突复杂度conij可构造为

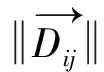
(11)

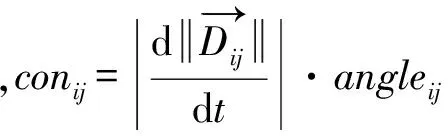
当船舶的运动趋势不变时，冲突因子conij根据式(3)～式(7)，随船舶的航迹交叉角和船舶相对距离的变化而变化。

2.3水上交通流的复杂度

对于一个交通关系单元VCij，其交通复杂度由第Ⅰ类复杂性denij和第Ⅱ类复杂性conij构成，因此其复杂性可采用加和形式定义为complexityij，可表示为

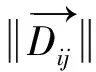
(12)

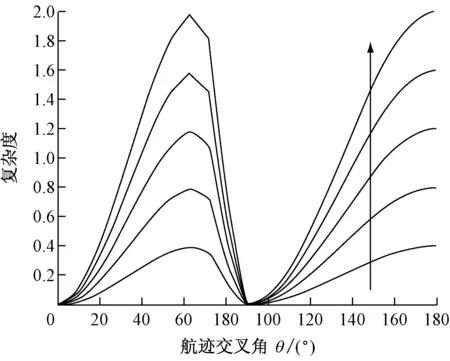
为满足第1节中提出的条件，对式(12)中的参数λgt;0,αgt;0做调整。设船舶相聚0.2 n mile时由距离因子引起的复杂度是间距为0.5 n mile时的3倍；67.5°交角下间距0.5 n mile时的管制复杂度是间距1.5 n mile下的15倍，间距3 n mile的复杂度趋近于0。由此可以确定参数α=1.81，λ=300.21。

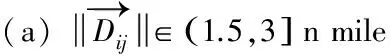
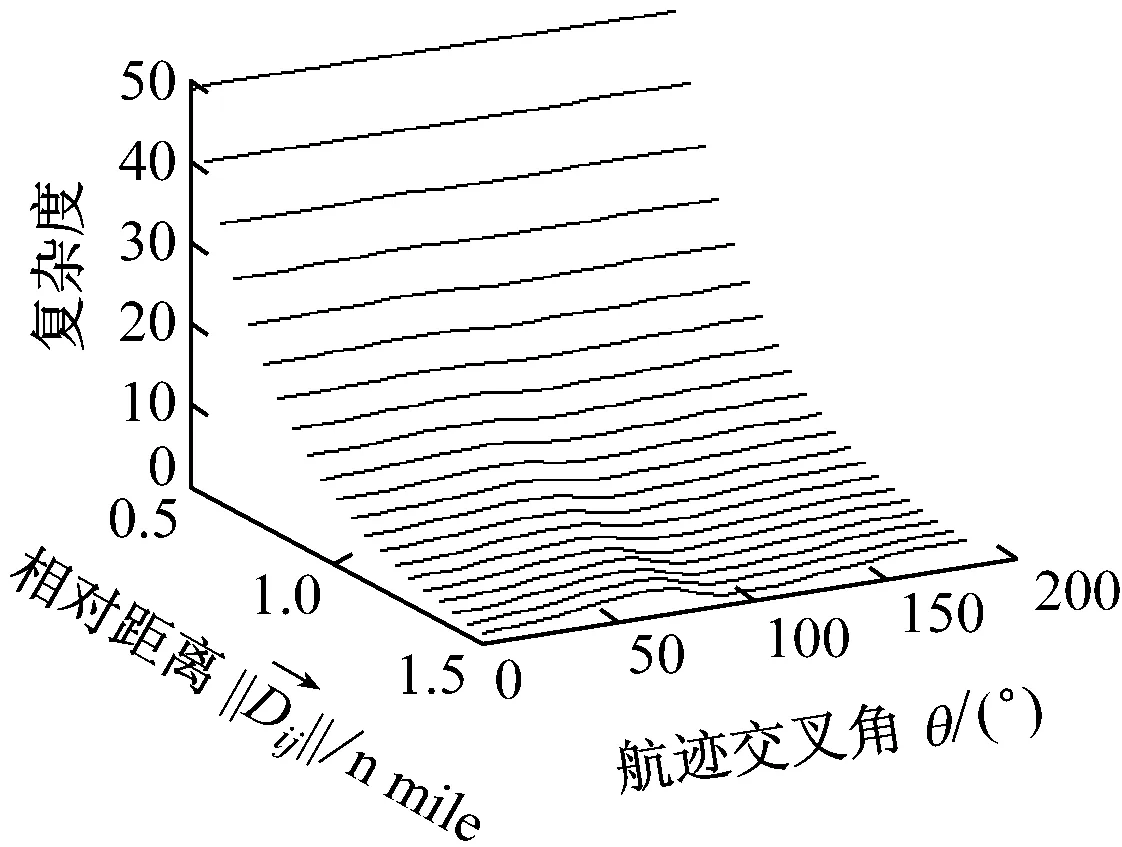
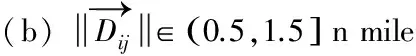
图7 交通关系单元复杂性函数族曲线

在研究水域，由于该水域交通流复杂性具有时间、空间分布的不同，计算该水域总体的交通流复杂度对进行水上交通管理的意义不大。相反，以单艘船舶i为视角，计算该水域内所有与i船有关的交通关系单元的复杂性并累加，可以得到此时该船坐标下的交通流复杂度。设第i艘船舶的复杂度为C(i)，将与i有关的交通关系单元的交通复杂度相加即可得到i船面临的交通复杂度。

(13)

由式(13)可得到该水域各船舶的复杂度，据此可获得交通流复杂度的空间分布，为交通管理提供参考。

3 模型验证

以深圳西海域的模拟交通流数据为基础，计算封闭航道内单向航行船舶的交通复杂度，得到该水域的水上交通流复杂度的空间分布情况;根据该水域的速度场分布和复杂度空间分布分析复杂度模型的合理性;根据该水域的航道结构，将该水域分为A～D4个扇区(见图8)。

图8中,1～2为航道入口，3～6为航道出口。由入口1、入口2进入该水域的船舶在A区交汇，并形成三个方向的交通流，分别向B、C、D区航行；B区是一个典型的“Y”字型航道,由A区驶入的船舶分别在出口3、出口4驶出B区；C区是一条进港航道，其特点是航道宽度窄；D区航道属于弯曲航道，船舶可由A区驶向出口6。

3.1交通流的速度场分布

根据深圳西部海域模拟交通流做出船舶速度场分布图(见图9)。从图中可以看出,对应图8的A区域由于存在不同航路的船舶汇入和汇出，会导致图9中a点的交通密度偏大，船舶航迹存在交叉，可以预见该水域的交通复杂度较高。由入口1进来的船舶分成北、东两支交通流，北向交通流是在A区的北部汇入的，由入口2驶向B区的交通流；东向交通流在A区南部横越入口2并驶向D区的交通流。

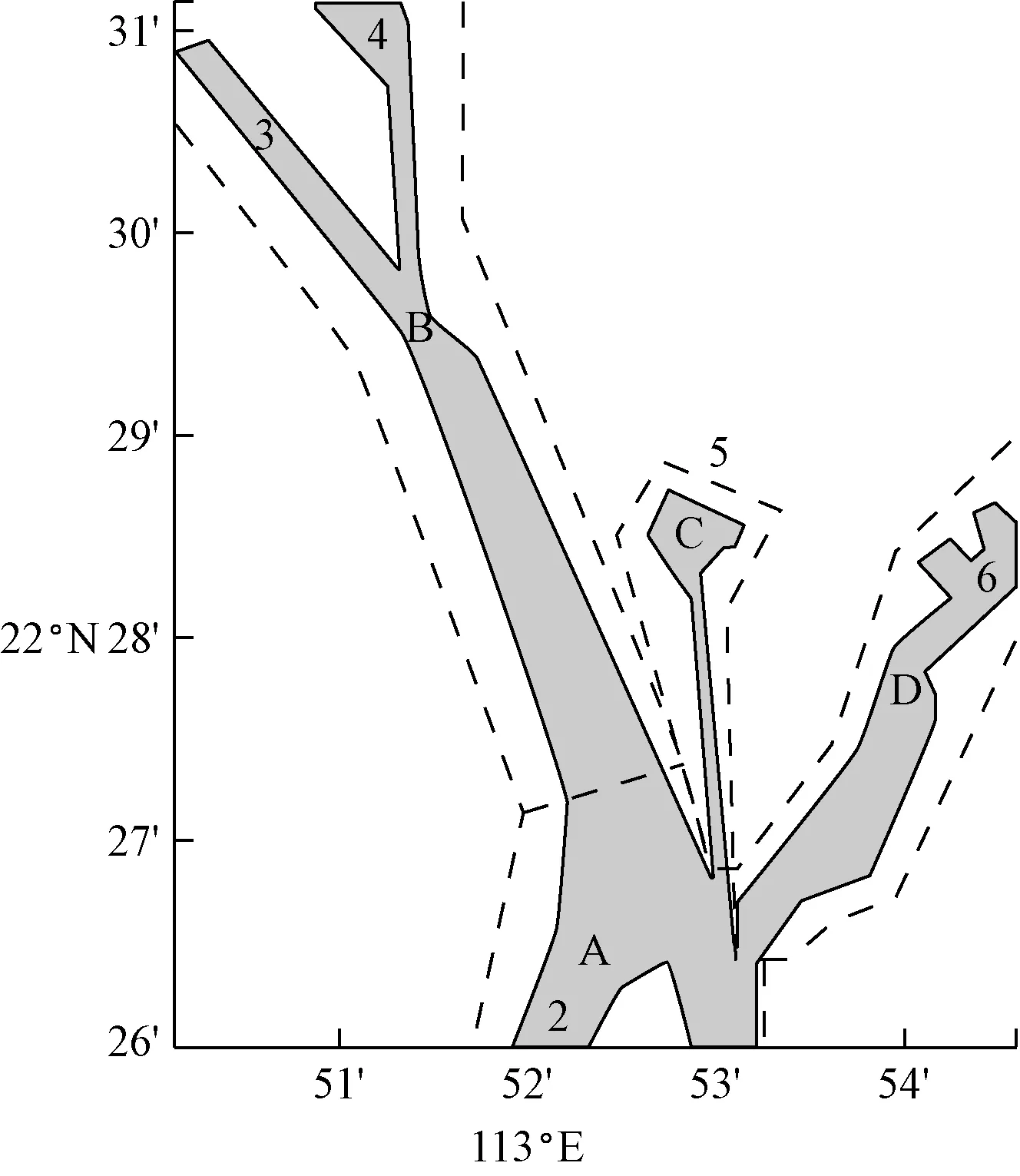
图8 深圳西部海域航道扇区划分

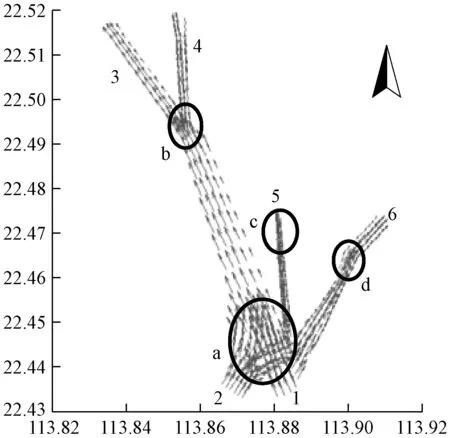
图9 深圳西部海域速度场分布情况

在B区域，由于存在航道的分叉，交通流在b点分流。船舶在b点分别向出口3和出口4航行，因此在b点船舶航向存在交叉，可以预见该水域的交通复杂度较高。

在C区域，虽然不存在船舶航迹的交叉，但是由于航道由宽变窄，船舶间的相对距离减小，可以预见其复杂程度较高。

在D区域,航道由宽变窄，又由窄变宽，可以预见其复杂度沿航道方向由小变大，在d点处达到最大，再由大变小。

3.2交通流的复杂度分布

根据式(13)分扇区计算船舶的复杂度情况，计算出各点船舶的复杂度后，对数据进行插值，得到深圳西部海域复杂度分布情况图(见图10)。

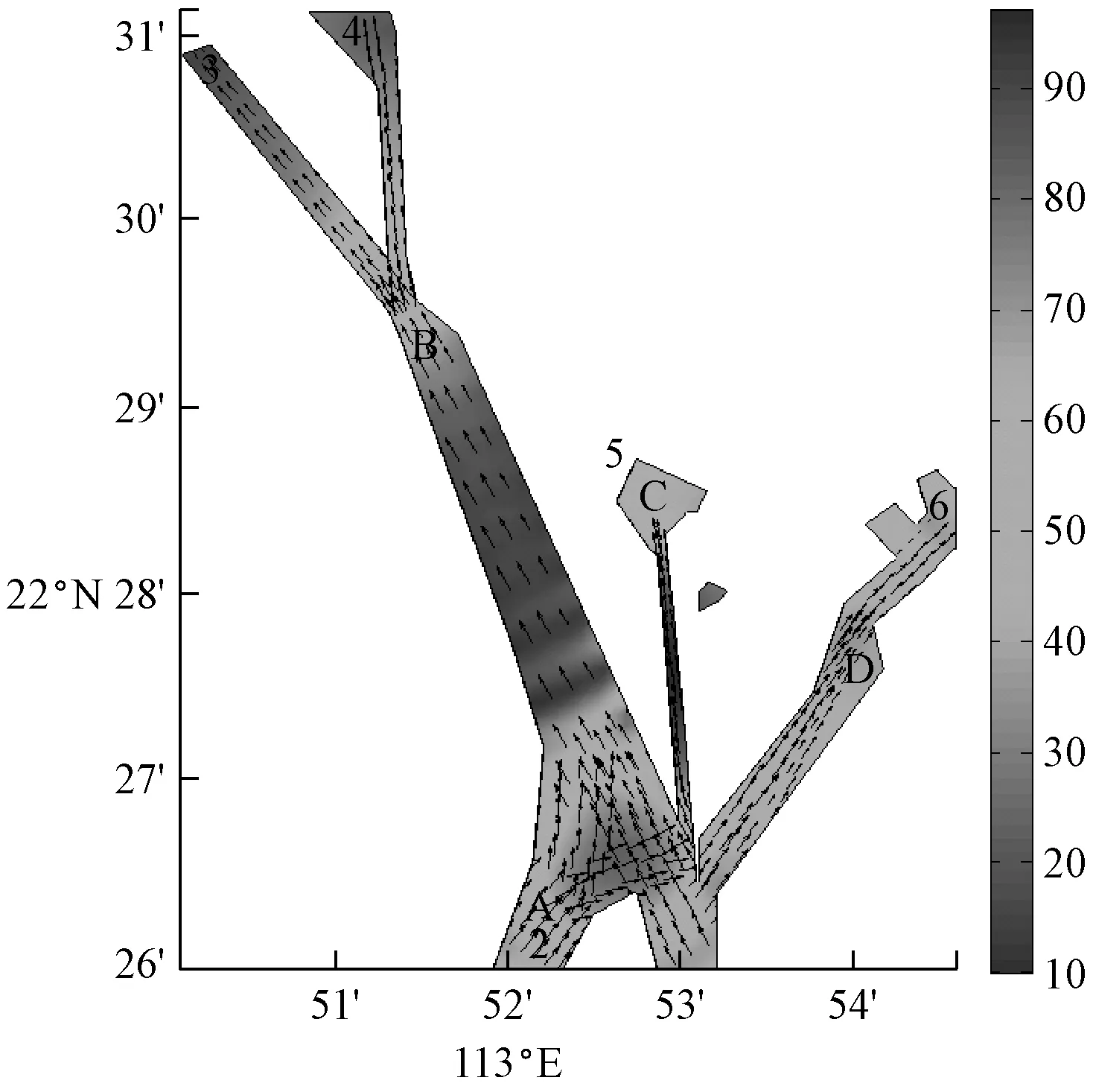
图10 深圳西部海域复杂度分布情况

图10为深圳西部海域复杂度分布情况，图中各点代表在该点处船舶交通复杂度的值。从图中可以看出,C区域的复杂度最高，A区域交通流较高，B、D区域的交通流复杂度次之，其他区域复杂度较低。

图11为图10的局部放大图。由图11(A)可知，A区域的交通冲突主要有交通流A1和A3大角度交叉、交通流A4汇入A2。因此图中A3与A4的冲突区域复杂度更高，在80～90；而A4汇入A2的交通复杂度相对较低，在50～70。

由图11(B)可知，B区域的船舶交通结构主要是：交通流B1在交叉口分流为B2和B3。由于交通流B1的船舶间距大，船舶间的航向相对一致，因此交通流B1的复杂度较低，在10～20；B2和B3航道较窄，距离交叉口较近的船舶未完全脱离复杂区域，因此复杂度较高，随着船舶远离交叉口，逐渐下降；B区域中的航道交叉口是交通复杂度最高的区域，该水域船舶间距减小，船舶航向存在交叉，因此其复杂度较高，大约在50～60。

由图10可知，C区域的交通复杂度最高。由于该区域航道较窄，而船舶数量较多，与B区域中交通流B1的数量相等，大部分船舶间距lt;0.5 n mile，船舶密度较大，因此交通复杂度最高。

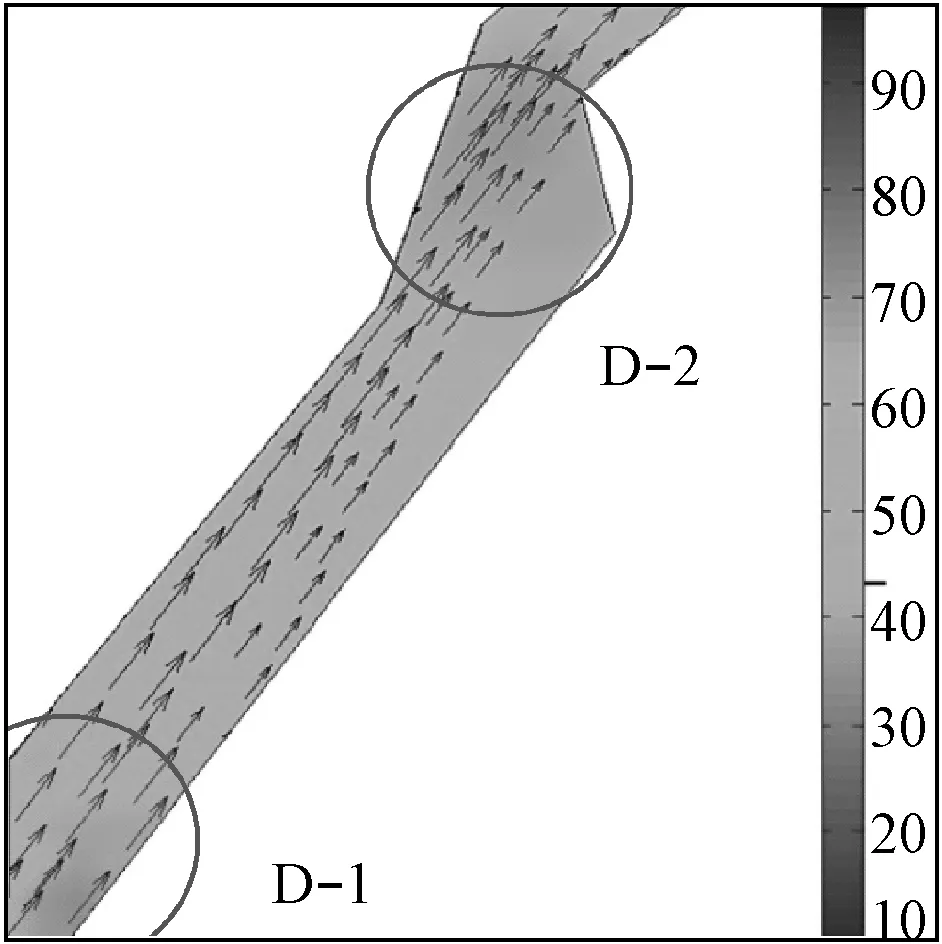
图11中的D区航道与A区相连，船舶由A区进入D区(如图11(D1))，进入D区的船舶间距增加，因此该区入口处(D-1)船舶交通流复杂度较低，大约在30～40；在D区的D-2处，航道曲折，船舶间距减小，船舶频繁变向船舶航向交叉，存在潜在的交通冲突，因此该处的交通复杂度也相对较高，大约在60～70；在D-3处，航道变宽船舶间距较大，交通密度小，船舶航向保持一致,因此该处交通复杂度逐渐减小。

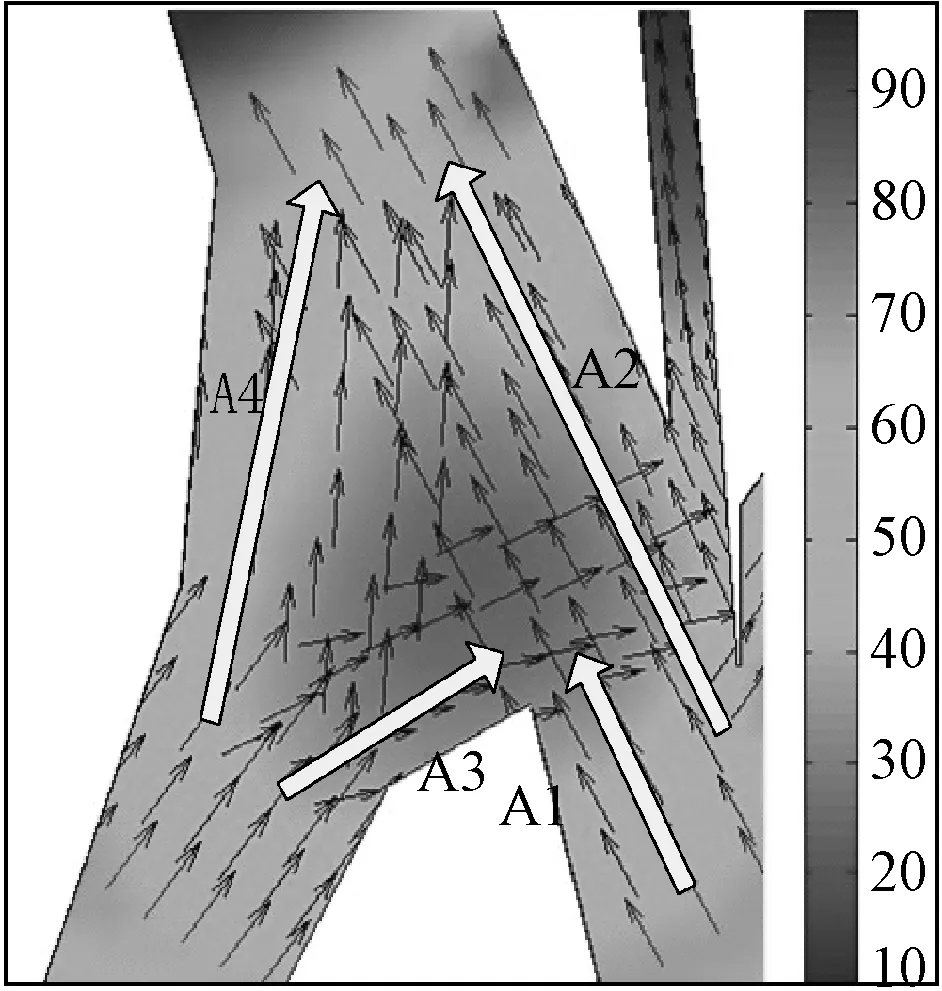
(A)

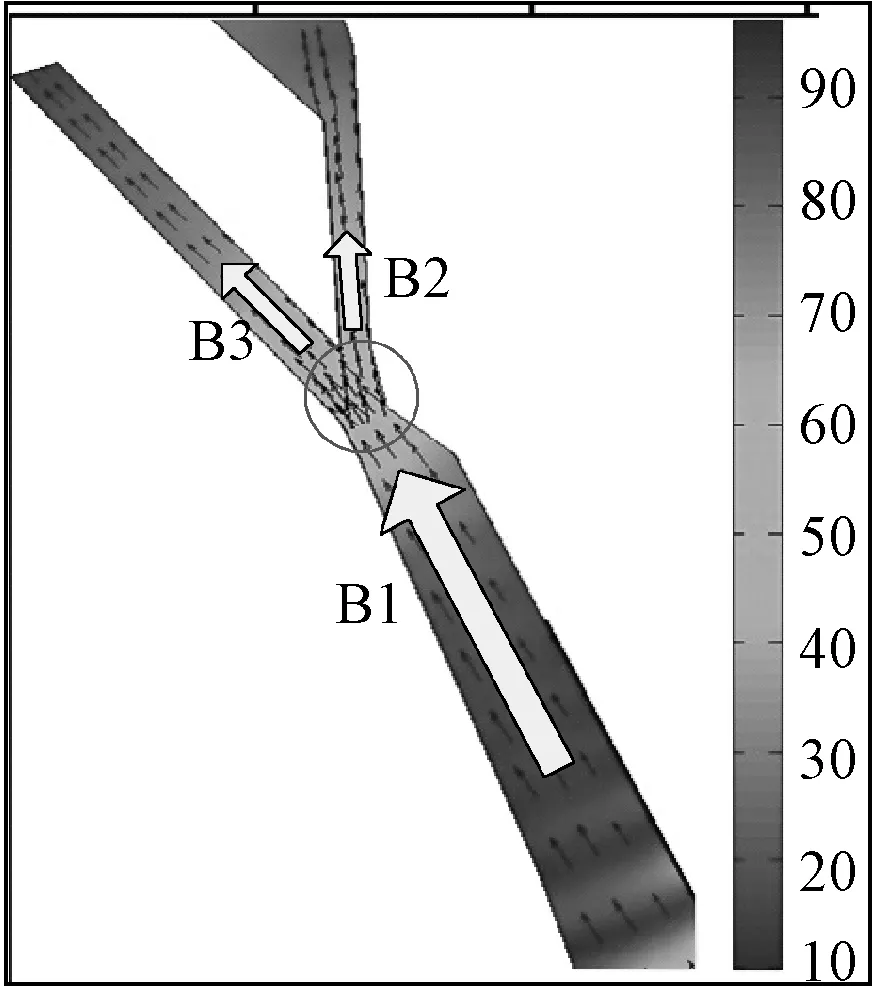
(B)

(D1)

(D2)

4 结 语

分析狭窄水域的船舶交通流特征，得出水上交通流复杂度空间分布的不均匀性;应用航空领域交通结构的复杂性建模的方法，选取交通密度和交通冲突作为复杂度影响因子，建立水上交通流复杂度模型，并对模型进行验证。结果表明,该模型能够反应出研究水域交通复杂度的空间分布，并能为水上交通管理资源分配提供参考依据。

本文仅考虑单一船型的复杂度，没有讨论不同船型引起的复杂度模型参数的变化；默认航道的自然条件相同，没有考虑自然环境对复杂度的影响。基于不同船型的交通复杂度和通航环境对交通流复杂度的影响有待进行进一步研究。

[1] 杨翔. 船舶交通流量预测方法研究[D]. 大连：大连海事大学, 2006.

[2] 赵景丽. 基于排队论的沿海港口航道通过能力及服务水平研究[D]. 青岛：中国海洋大学, 2010.

[3] 邵长丰, 方祥麟. 船舶交通流的流体模型[J]. 大连海事大学学报, 2002, 28(1): 52-55.

[4] 朱俊, 张玮. 基于跟驰理论的内河航道通过能力计算模型[J]. 交通运输工程学报, 2009,9(5):83-87.

[5] 曹宝贵. 交通流复杂动态特性与交通拥堵问题研究[D]. 长春：吉林大学, 2010.

[6] Laudeman IV, Shelden S G, Branstrom R, et al. Dynamic Density: An Air Traffic Management Metric[R]. NAS 1.15:112226, NASA/TM-1998-112226. USA Springfield: NTIS, 1998.

[7] CHATTERJI G B, SRIDHAR B. Measures for Air Traffic Controller Workload Prediction[C]. // 1st AIAA Aircraft, Technology Integration, and Operations Forum. USA. Los Angeles: AIAA Press, 2001.

[8] 戴福青, 洪兰收. 空域交通复杂度计算方法研究[J]. 中国民航大学学报, 2010, 28(3): 1-4.

[9] LEE K. Describing Airspace Complexity: Airspace Response to Disturbances [D]. Atlanta: Georgia Institute of Technology, 2008.

[10] Delahaye D, Puechmorel S. Air Traffic Complexity: Towards Intrinsic Metrics[C]. // the 3rd US/Europe Air Traffic Management Research amp; Development Seminar. Italy Napoli: EUROCONTROL Press, 2000.

[11] DELAHAYE D, PAIMBLANC P, PUECHMOREL S, et al. A New Air Traffic Complexity Metric Based on Dynamical System Modelization[C]. // The 21st Digital Avionics Systems Conference. USA Irvine: IEEE/AIAA Press, 2002.

[12] ZHANG C, ZHANG J, HU M. Air Traffic Complexity Based on Alliance Effects[C]. // The 28thDigital Avionics Systems Conference. USA Seattle: IEEE/AIAA Press, 2009.

[13] 叶博嘉, 胡明华, 张晨, 等. 基于交通结构的空中交通复杂性建模[J]. 交通运输系统工程与信息, 2012, 12 (1): 166-172.

[14] 刘峰涛, 贺国光. 基于近似熵和统计复杂度的交通流复杂性测度[J]. 中国公路学报, 2007,20 (4):108-112.

[15] 张勇, 关伟. 基于联合熵和C0复杂度的交通流复杂性测度[J]. 计算机工程与应用, 2010,46(15): 22-24.

[16] 杜安民. 基于标准船型的港口航道通过能力研究[D]. 大连：大连理工大学, 2008.

[17] TOYODA S, FUJII Y. Marine Traffic Engineering[J]. Journal of Navigation, 1971, 24 (2): 24-30.

[18] MONTEWKA J, HINZ T, KUJALA P, et al. Probability Modelling of Vessel Collisions[J]. Reliability Engineering and System Safety, 2010, 95 (5):573-589.

ModelingofMarineTrafficFlowStructureComplexity

WENYuanqiao1,2,HUANGYamin1,YANGJunlan1,XIAOChangshi1,2,ZHOUChunhui1,2,WUXiaochun1,2
(1. School of Navigation, Wuhan University of Technology, Wuhan 430063, China; 2. Hubei Inland Shipping Technology Key Laboratory, Wuhan 430063, China)

A model of marine traffic complexity is developed to address the problem of measuring marine traffic flow complexity in terms of its structure. The model, in which the traffic density factor and conflict factors are considered, reflects the traffic complexity and traffic characteristics including the relative distance, speed of ships pair-wise and the intersecting trajectory. The model reveals the spatial distribution regularities of the marine traffic complexity. The simulated data of Shenzhen West Sea are used to verify the model. The verification tests show that the model sensitively and accurately reflects the characteristics of the marine traffic in terms of its complexity.

waterway transportation; traffic flow; traffic structure; complexity modeling; spatial distribution

2014-01-20

国家自然科学基金青年科学基金(51209166)；国家自然科学基金(51179147)

文元桥(1975-) ，男，湖北松滋人，教授，主要从事水上交通安全与环境研究。E-mail:3444324@qq.com.

1000-4653(2014)02-0062-07

U692

A