CKF在SINS动基座大失准角初始对准中的应用
2014-11-30于飞,孙骞,张亚
于 飞, 孙 骞, 张 亚
(哈尔滨工程大学 自动化学院,哈尔滨 150001)
CKF在SINS动基座大失准角初始对准中的应用
于 飞, 孙 骞, 张 亚
(哈尔滨工程大学 自动化学院,哈尔滨 150001)
为了提高动机座捷联惯导系统初始对准的精度,在推导动基座大方位失准角非线性模型的基础上,提出一种基于容积卡尔曼滤波法的动基座初始对准算法,并对提出的算法进行仿真和试验验证。结果表明,与传统的无迹卡尔曼方法相比,利用该方法能够在更短的时间内更准确地完成精对准过程。
船舶工程;初始对准;动机座;大方位失准角;容积卡尔曼滤波
初始对准技术是捷联惯性导航系统(Strapdown Inertial Navigation System, SINS)的关键技术之一,对准精度和对准速度是其重要技术指标。[1]传统的初始对准的精对准过程是:利用经典Φ角法或Ψ角法推导出小失准角条件下的线性微分方程误差模型,然后利用标准Kalman滤波最优估计方法解决SINS初始对准问题。[2-3]但是在水面舰船航行过程中,尤其是在海况不佳时,载体会产生大幅晃动,方位粗对准的精度将很难得到保证。[4]当失准角较大时,线性模型不能正确地描述真实的系统,需要利用非线性模型描述SINS的误差特性。
对于非线性系统,最常用的滤波方法为扩展卡尔曼滤波(Extend Kalman Filter, EKF)和无迹卡尔曼滤波(Unscented Kalman Filter, UKF)。EKF实现简便、使用广泛,但是当系统为强非线性时,很容易产生线性化误差,造成滤波器精度下降,甚至发散。[5]UKF采用UT变换(Unscented Transformation, UT)取代局部线性化,虽然精度高于EKF,但是当处理高维数系统时,容易出现“维数灾难”。[6-7]近期提出的容积卡尔曼滤波(Cubature Kalman Filter, CKF)根据Cubature变换,通过计算一组经过非线性系统方程转换的具有相同权重的点集来给出下一时刻系统状态的预测结果。[8-9]由于其估计精度高、不容易发散且计算量小,CKF在非线性滤波问题中的应用越来越广泛。文献[10]首先将CKF应用到系统的初始对准中,虽然与传统滤波器相比估计结果有了很大改善,但是分析仅限于仿真;文献[11]将CKF滤波器应用到SINS大方位失准角初始对准中,但是只分析了静基座下的仿真和实验。目前很少有文献对动机座条件下的大失准角初始对准进行分析,而舰船绝大多数时间是处于动机座下的,因此在文献[11]的基础上,利用欧拉平台误差角描述动基座下大失准角SINS非线性误差模型,详细分析CKF滤波在动基座SINS初始对准中的应用。
1 SINS大失准角误差模型
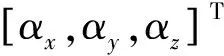
(1)
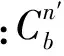
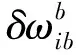
(2)
速度误差方程[12]为
(3)


(4)
由于陀螺仪和加速度计误差均由常值误差和零均值高斯白噪声组成,因此其微分方程为
(5)
位置误差方程由经纬度误差δλ和δφ组成,
(6)
式(6)中:RM,RN分别为地球子午面半径和卯酉面半径;φ为当地纬度值;vx,vy分别为东向和北向速度。
2 系统建模与CKF滤波算法
2.1非线性SINS建模

系统噪声向量为

以SINS与多普勒计程仪的速度之差作为观测量,建立状态方程和观测方程

(7)
式(7)中:状态转移矩阵F(X)和系统噪声驱动阵G的具体表达式参考式(2)~式(6),W~N(0,Q);量测矩阵H=[02×2,I2×2,02×8];V为量测噪声,V~N(0,R)。
2.2CKF滤波算法
CKF滤波算法是一种基于高斯假设的贝叶斯滤波方法,它根据Cubature准则,通过对2n个同等权值的Cubature点进行非线性方程转换后产生新的点来给出下一时刻系统的状态,从而完成预测。与传统的UKF滤波方法相比,CKF的采样点较少,能够降低计算量、提高滤波的收敛速度;CKF中的Cubature点集是通过积分得到的,权值永远为正,可以有效解决UKF在高维系统中权值为负时出现的滤波发散问题,因此CKF滤波算法的数值稳定性及滤波精度均优于UKF。[13-14]
考虑如下的非线性离散状态空间模型
(8)
式(8)中:xk∈Rn和zk∈Rm分别为k时刻的状态向量和量测向量;f(·)和h(·)为系统状态和量测的非线性转换;过程噪声wk和量测噪声vk为互不相关的高斯白噪声,且满足wk~(0,Qk),vk~(0,Rk)。
CKF滤波方法的具体算法流程[8,14]为
Yi,k|k-1=h(Xi,k|k-1)
3 仿真分析和试验验证
3.1仿真及分析
为验证动基座初始对准中CKF滤波方法的性能,进行仿真试验。设水面舰船的横摇、纵摇和航向角分别为Ψ,θ,γ,摇摆过程的数学建模为
(9)
式(9)中:摇摆幅值分别为:θm=10°,Ψm=6°,γm=8°;摇摆周期为:Tθ=10 s,TΨ=6 s,Tγ=8 s;初始姿态角分别为:θk=Ψk=0°,γk=30°。水面舰船的东向和北向初始速度为vx=vy=5 m/s,在0~30 s内作匀加速直线运动;东向和北向加速度为ax=ay=0.2 m/s2,30 s之后作匀速直线运动。舰船初始经纬度分别为东经126.670 5°、北纬45.779 6°,初始水平失准角为φe=φn=1°,初始方位失准角为φu=10°,陀螺常值漂移为0.01(°)/h,陀螺随机噪声为0.005(°)/h,加速度计零偏为10-5g0,加速度计随机噪声为0.5×10-5g0。
在上述条件下,分别利用UKF方法和CKF方法对失准角误差估计进行仿真,仿真时间为600 s,仿真得到的水平失准角及方位失准角估计误差曲线见图1和图2。
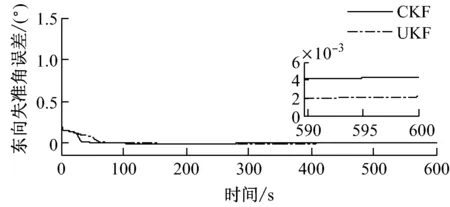
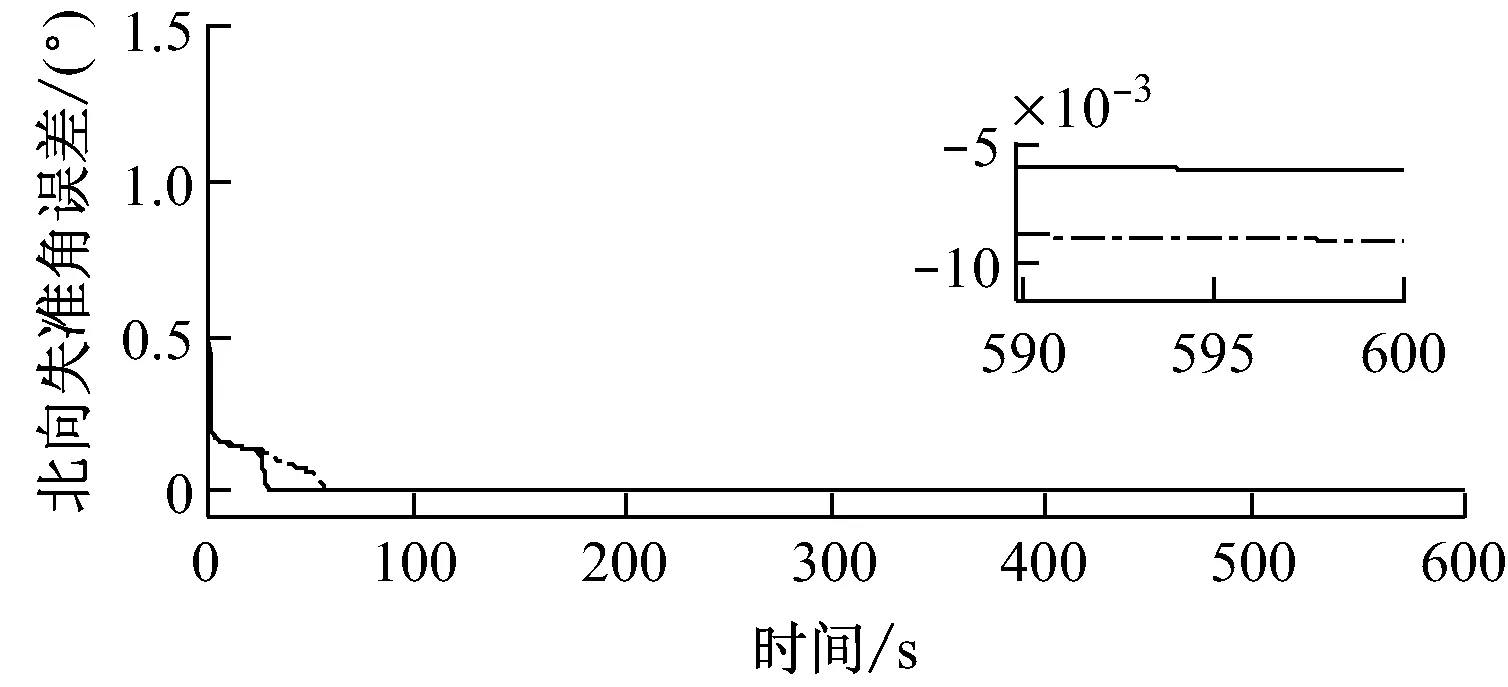
图1 水平失准角估计误差对比曲线

图2 方位失准角估计误差对比曲线
由图1和图2可以看出,在动基座方位大失准角的情况下,对于水平失准角误差,CKF和UKF的收敛速度和估计精度基本相同;对于方位失准角误差,CKF的收敛速度明显比UKF快,而且在600 s处,CKF的估计稳定值为-0.47°,UKF的估计稳定值为-0.54°。因此,CKF的估计精度高于UKF。仿真结果表明,CKF能够解决动基座方位大失准角初始对准问题,且收敛速度快、对准精度高。
3.2试验验证
采用实验室自行研制的高精度光纤陀螺惯导系统在某地进行试验,试验设备主要包括光纤陀螺惯导系统、多普勒计程仪、PHINS、水面舰船、导航计算机及相关电源,其中自研光纤陀螺惯导系统见图3,舰载实验设备安装见图4。
舰船初始经纬度分别为东经126.670 5°、北纬45.779 6°,初始横摇角、纵摇角及航向角分别为0.05°、0.73°、212.5°,水面舰船的初始状态为系泊状态,加速80 s至东向速度为4.8 m/s、北向速度为7.6 m/s,随后舰船为匀速直线运动。取60 s粗对准结果作为精对准开始时的初始失准角,则初始失准角为0.896°、0.434°、4.158°。分别采用此处所提算法和传统的UKF滤波算法对系统状态变量进行估计。由于采用这两种方法后水平失准角误差估计精度均较高且收敛速度均较快,因此只给出方位失准角误差对比曲线(见图5)。

图3 实验室自研光纤陀螺惯导系统

图4 实船试验设备图

图5 方位失准角估计误差对比曲线
由图5可以看出,采用UKF滤波方法后,曲线在600 s后趋于稳定,稳定值为-0.196°;采用CKF滤波方法后,曲线在400 s后趋于稳定,稳定值为-0.185°。因此,动基座方位大失准角条件下,CKF的估计精度比UKF高,且估计时间比UKF短,与仿真结果一致。
4 结 语
推导出动机座SINS方位大失准角的非线性误差方程,并建立滤波模型;分析CKF滤波算法,从理论上证实了CKF的优势,并分别对CKF和UKF两种方法进行了仿真。仿真结果表明,采用CKF方法后滤波精度和收敛速度均优于UKF方法。最后,利用实验室自研的光纤捷联惯导系统进行实船试验,试验结果与仿真结论相同,进一步证实CKF在动基座大方位失准角SINS初始对准中的可行性和优越性,为工程上动基座大失准角初始对准提供了一种新的方式。
[1] 高伟,张亚,奔粤阳,等. 旋转式惯导系统刻度因数误差的分析与补偿[J].中国航海,2012, 35(3):1-4.
[2] 严恭敏,严卫生,徐德民. 简化UKF滤波在SINS大失准角初始对准中的应用[J]. 中国惯性技术学报, 2008, 16(3): 253-264.
[3] 秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M]. 西安:西北工业大学出版社,1998.
[4] 郝艳玲,杨峻巍,陈亮,等. 基于SRCKF的水下航行器动基座初始对准技术[J].华中科技大学学报:自然科学版, 2012, 40(2): 123-127.
[5] 李中兵,张欢仁.基于扩展卡尔曼滤波的船舶电力推进系统仿真[J]. 中国航海,2011, 34(4):45-50.
[6] 顾冬晴,秦永元. 船用捷联惯导系统运动中对准的UKF设计[J]. 系统工程与电子技术,2006,28(8):1218-1220.
[7] GE Quanbo, LI Wenbin, WEN Chenglin. SCKF-STF-CN: a Universal Nonlinear Filter for Maneuver Target Tracking [J]. Journal of Zhejiang University-Science C: Compute amp; Electron, 2011, 12(8): 678-686.
[8] ARASATNAM I, HAYKIN S. Cubature Kalman Filters [J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1 254-1269.
[9] ARASARATNAM I, HAYKIN S. Cubature Kalman Smoothers [J]. Automatica, 2011(47): 2245-2250.
[10] KUMAR P, BHARANI C, GU Dawei. Cubature Information Filter and Its Applications [C]. 2011 American Control Conference. San Francisco, CA, USA, 2011.
[11] 孙枫, 唐李军. 基于CKF的SINS大方位失准角初始对准[J]. 仪器仪表学报, 2012, 33(2): 327-333.
[12] 龙瑞, 秦永元, 夏家和. CDKF在捷联惯导系统大失准角初始对准的应用[J]. 西北工业大学学报, 2010, 28(3): 364-368.
[13] 孙枫, 唐李军. Cubature卡尔曼滤波-卡尔曼滤波算法[J]. 控制与决策, 2012, 27(10): 1 561-1 565.
[14] ARASARATNAM I, HAYKIN S. Cubature Kalman Filter for Continuous-Discrete System: Theory and Simulation [J]. IEEE Transactions on Signal Processing, 2010, 58(10): 4 977-4 993.
ApplyingCKFtoInitialAlignmentofSINSonDynamicBasewithaLargeMisalignmentAngle
YUFei,SUNQian,ZHANGYa
(College of Automation, Harbin Engineering University, Harbin 150001, China)
The non-linear model of the system on the dynamic base with large azimuth misalignment angle is derived and the dynamic base initial alignment algorithm based on Cubature Kalman filter is presented. The simulation and experiment results show that the fine alignment with Cubature Kalman filter achieves better accuracy in shorter time than the one with Unscented Kalman filter.
ship engineering; initial alignment; dynamic base; large azimuth misalignment angle; Cubature Kalman filter
2014-01-28
国家自然科学基金(51179039);武器装备预研基金(9140A09040211CB0102)
于 飞 (1974-), 男, 黑龙江哈尔滨人,教授,博士生导师,从事捷联惯性导航系统及其组合导航技术研究。E-mail: yufei@hrbeu.edu.cn.
1000-4653(2014)02-0048-05
U666.12
A
