基于热点解和差分进化的多目标聚类集成算法

李 莉，李妍琰

（1.河南工程学院 计算机学院，河南 郑州451191；2.河南财经政法大学 计算机与信息工程学院，河南 郑州450002）

0 引 言

相对于传统的聚类算法，多目标聚类能够综合考虑多种已有聚类方法的评价标准，避免了单一评价标准对数据结构描述存在偏差的影响。典型的多目标聚类算法如Handl等人［1］提出的多目标进化聚类算法 MOCK，及Saha等人［2］提出的基于模拟退火的多目标聚类算法VAMOSA。国内也有学者提出了相应的多目标聚类算法，张欢等人［3］改进MOCK算法并将其应用于挖掘机故障数据的聚类分析中，取得了比k均值更低的错误识别率。秦亮等人［4］提出的算法中采用了与MOCK相同的目标函数，设计了一种免疫克隆选择算法对其进行优化，取得了比MOCK运算速度更快、错误率更低的识别结果。聚类集成是另外一种有效提高传统聚类方法性能的技术，将多个聚类成员所得的聚类结果进行综合，从而得到好于单一聚类成员的结果。由于多目标聚类最终得到多个不同的解，因此将其与聚类集成技术结合是可行的。并且多目标聚类集成技术可以进一步提高聚类结果的质量，解决多目标聚类中不易自动选取单个解的问题。Qian等人［5］以MOCK算法为基础，将聚类得到的所有候选解集成，并用于文本图像的分割中。Zhu等人［6］则将多目标进化聚类与软子空间聚类相结合，提出了一种多目标聚类集成算法，其在集成阶段利用图分割方法将所有解集成。上述算法将多目标聚类与集成技术进行了简单的结合，但多目标聚类算法所得的解集中包含多个类数下的划分结果，存在大量欠划分或者过划分的解，与真实的数据结构相差巨大，如果直接利用所有的解进行集成，其聚类结果会受质量较差解的影响，通常只能达到所有解的平均水平。另外，由于个体编码所表达的类数是不同的，常见的交叉变异算子不能很好应用于聚类过程中，构建合理高效的多目标聚类算法也是保证聚类质量的重要环节。为此，提出了一种基于热点解搜索和差分进化的多目标聚类集成算法，利用高效的差分进化机制实现优化，并针对聚类过程中编码长度不一的情况，对差分进化的交叉和变异算子进行了相应地改进；在优化过程中不断找出当前种群里的热点解，用其作为差分进化中的 “best”个体，引导种群的优化方向，加强潜在最优解区域的搜索；在后续的集成操作中，再基于热点解的概念对优化所得的解集进行筛选，去除了质量较差解对集成结果的影响。

1 多目标优化问题描述与热点解的搜索方法

1.1 多目标优化问题描述

多目标优化问题的定义为

式中：x——解空间的n维变量，gi（x）——目标空间的第i个函数取值，一共有m个目标函数。

在式 （1）中每个目标函数均要达到最小化，但各个目标函数之间存在一定的矛盾关系，一部分目标函数取值的减小会引起另一部分目标函数取值的增加。因此理想状态下同时最小化各个目标函数是无法实现的，其最终得到的实际是一组折中解集。该解集称为Pareto解集，其定义如下：

（1）Pareto占优：对于解空间的变量x1和x2，若对于所有的目标函数均有gi（x1）≤gi（x2），并且存在目标函数gj（x）使得gj（x1）＜gj（x2），则称解x1对x2Pareto占优。

（2）Pareto解集：若解空间其它变量均不能Pareto占优解x1，则称x1为Pareto占优解。这样的解通常存在多个，它们之间互不占优，其构成的集合称为Pareto解集，即优化所得的折中解集。

在聚类算法中，存在多种描述聚类质量的评价标准。这些标准均从某一方面描述聚类的质量，具有一定的片面性。而它们之间又存在一定的矛盾关系，例如评价类内方差的标准会倾向于将每个样本看作一个独立的类，而评价类间距离总量的标准又会倾向于将整个数据看作一个类。可见，将聚类算法转换为一个多目标优化问题既是合理的，又能全面描述数据的结构［7］。

1.2 热点解的搜索方法

热点解是指在Pareto解集中目标函数取值发生突变的位置上的解。即相对于周围的Pareto占优解，热点解的一部分目标函数值大幅增大 （或减小），而另一部分目标函数值减小 （或增大）的幅度却很小。这种幅值的变化可以通过式 （2）进行描述

式中：T——解x1相对于x2，其目标函数取值减小的总量与目标函数取值增大的总量之比。为了不受函数取值量级的影响，所有目标函数的取值必须先进行归一化处理［8］。

用S表示一个Pareto解集的子集，该子集的元素在目标函数空间上的欧式距离相近。对于任意一个解x∈S，按照式 （3）找出其相对于S中其它解的最小变化量u（x，S）。它表示每单位衰减量 （即目标函数值增加总量）下解x在一些目标函数上的最小提升量 （即减小量）。再按照式 （4）找出所有解的最小变化量中的最大值u（x＊，S），x＊即为区域S中的热点解

在多目标聚类中，热点解往往对应Pareto解集中一些关键的聚类划分结果，这些解能够很好反映数据的真实结构。数据如图1所示。

图1 数据类数变化过程中目标函数取值变化

当划分结果由一个类变化到2个类时，类内方差显著减小，而类间距离总量增大相对较小；当变化到8个类时，类内方差减小较小，类间距离总量则会有较大增加。

2 MCEASKD的设计

本文提出的多目标聚类集成算法以差分进化算子为基本搜索算子，在进化和集成过程中均利用了热点解以提高求解的质量。

2.1 目标函数设计

MCEASKD同时优化2个目标函数，分别为常见的类内方差和类间距离总量，其具体定义如式 （5）和式 （6）所示

式中：k——个体x所表示的总类数，d——数据的维数，Ni——第i个类的样本总数，xij——第i个类在第j维上的类中心取值，zpj——第i个类中第p个样本在第j维上的取值。

2.2 改进的差分进化算法

MCEASKD以概率选择的形式使用了2种差分进化算子，分别为DE／rand／1／bin和DE／best／1／bin。二者变异部分的定义如式 （7）所示

式中：F——张量因子，个体a、b、c从当前种群中选取，并且保证a≠b≠c。对于算子DE／rand／1／bin，个体a、b、c均从种群中随机选取，用于加强种群在整个空间中的全局搜索能力；而对于DE／best／1／bin，个体a则从当前找到的热点解中随机选取，个体b、c从种群中随机选取，用于提高算法的收敛速度。2种差分进化算子交叉部分的定义如式 （8）所示

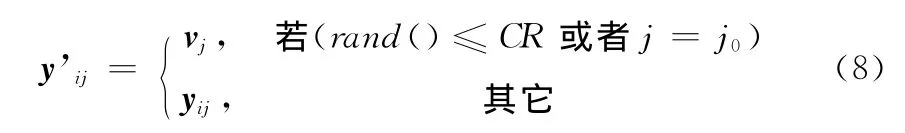
式中：CR——交叉率参数，个体i随机从种群中选取，且i≠a≠b≠c，j0表示随机选取的某一维变量，rand（）——0和1之间的随机数。

设定选择 DE／rand／1／bin的概率为ps，选择 DE／best／1／bin的概率为1－ps。在进化前期算法应加强全局搜索，在后期应加强热点解附近的搜索，因此本文设定的取值随进化代数线性增加，如式 （9）所示

式中：p0、p1和t0——预先设定值，t——当前进化代数，tmax——最大进化代数。

由于本文采用类中心编码的方式，个体之间的有效编码长度往往不同，传统的差分进化算子无法应用在聚类中。因此做了如下改进：假设个体x1、x2、x3、x4所表示的类数分别为k1、k2、k3和k4；找出类数最少的个体，设其编码长度为k·d＝min ｛k1、k2、k3、k4｝·d；然后分别从个体x1、x2、x3、x4中随机选取k个类的编码存入ya、yb、yc、yi中 （y的编码长度为k·d），再执行相应的差分进化算子，然后用新生成的yi’替换x4中相应位置的取值，最终得到新的解x’。

2.3 改进的集成操作

在集成操作之前，先将优化得到的Pareto解集按照某一目标函数取值 （如g1（x））升序排列。然后找出各个目标函数取值的最大和最小值，对其进行归一化处理。再将按照g1（x）的取值将所有解等分为h个区间，找出每个区间中的热点解，存入集合Sk。对于集合Sk中的每个解，在目标空间上按照欧式距离度量找到其l个最近邻Pareto占优解，存入集合Sn中。最后，按照文献 ［9］提出的基于超图分割的集成算法HGPA，将集合和中的所有解集成，集成的结果即为最终的聚类结果。

2.4 算法流程描述

MCEASKD的算法流程如下所示：①设定可选类数的范围为1～kmax，进化种群为P，进化代数t＝0，首先随机生成kmax个个体，它们所表示的类数依次为1、2、…、kmax，再随机生成剩余的｜P｜－kmax个个体，其中每个个体的类数在1和kmax之间随机选择，按式 （5）和式 （6）计算所有个体的目标函数值；②当进化代数t＜t0时，根据算子DE／rand／1／bin生成新个体，否则根据概率ps选择DE／rand／1／bin或DE／best／1／bin生成新个体；③反复执行步骤②，直到得到与种群P相同的个体数量，记为子代种群P’，将P和P’中的个体合并，按照NSGAII［10］中提出的非劣排序方法和拥挤距离方法更新种群P；④若达到最大进化代数tmax，则停止迭代，选出种群P中的所有Pareto解，再从中找出所有的热点解及其邻域个体，对其进行集成操作，输出集成后的结果，否则继续优化，令t＝t＋1。

3 实验与分析

选取三组UCI数据［11］用于验证所提算法 MCEASKD的有效性。这三组数据分别为Vehicle、Ionosphere和Sonar。它们的样本数量分别为846、351和208个，特征维数分别为18、34和60个，类数分别为4、2和2个。

为了更好的说明本文算法的性能，选取2种多目标聚类集成算法用于对比分析：第一种为文献 ［1］所提出的MOCK算法与本文所提基于热点解搜索的集成方法相结合而形成的新算法，记为MOCKE；第二种为本文算法不经过热点解的筛选而直接进行集成操作而形成的算法，记为MCEAD。MOCKE中多目标聚类环节的参数设置与文献［1］相同，集成环节参数设置与本文算法相同。MCEAD的所有参数设置均与本文算法相同。本文算法MCEASKD的具体参数设置为：种群P的大小为100，最大进化代数为tmax200，最大类数kmax为20，参数t0为50，p0和p1分别为0.05和0.4，差分进化的参数CR取值为0.9，张量因子F 对于 DE／rand／1／bin的取值为0.7，对于 DE／best／1／bin的取值为0.2，区间划分数量h为10，邻域个数l为4。

本文采用RI指标［12］和FM指标［13］来评价各种算法的聚类结果，2种指标的取值均是越大说明聚类结果越好。三组UCI数据在每种算法上均测试30次［14］，其测试所得的RI指标均值和FM指标均值分别见表1和表2。

可见，本文提出的算法MCEASKD无论在RI指标还是在FM指标上均高于2种对比算法的结果，其中RI取值提高了0.0021～0.0524，FM取值提高了0.0134～0.0591。此外，MCEASKD和MOCKE采用了相同的基于热点解筛选的集成操作，其对比结果说明提出的改进差分算子具有良好的寻优性能，使得所得Pareto解集的质量普遍好于MOCK算法所得结果，为后续集成操作提供了更多好的集成成员。而MCEASKD与MCEAD的区别在于是否在集成操作阶段使用了基于热点解的筛选步骤，对比结果说明本文提出的筛选方法可以有效去除Pareto解集中质量较差解对算法性能的影响。

表1 3种算法的测试结果在RI指标上的对比

表2 3种算法的测试结果在FM指标上的对比

本文算法中的区间划分数量h和邻域个数l决定着热点解的数量以及最后用于集成操作的解的数量，是算法中的重要参数。因此，此处以Vehicle数据为例，分析了上述2个参数对算法性能的影响。首先，将区间划分数量h由5变化到20，而保持邻域个数l始终为4，其结果如图2所示。

图2 区间划分数量h对算法质量的影响

其次，将区间划分数量h固定为10，而将邻域个数l由1变化到20，其结果如图3所示。

图3 邻域个数l对算法质量的影响

从图2和图3中的实验结果表明，区间划分数量h和邻域个数l均不宜过大；否则，会使得进化过程中选中的热点解数量过多，从而起不到引导种群进化方向的作用；还会使得集成操作之前的筛选步骤失效，一些质量较差的解会进入集成操作中，从而影响集成的质量。

4 结束语

本文提出了一种热点解搜索和差分进化的多目标聚类集成算法MCEASKD。该算法在优化过程和集成过程中均对若干热点解进行了搜索。这些热点解既能用于引导差分进化的搜索方向，提高了差分进化的寻优能力，还能用于在集成操作前筛选掉一些质量较差的Pareto占优解，提高了后续的聚类集成的效果。此外，提出了在差分进化算子中利用多个个体的最小编码部分进行变异和交叉，解决了聚类中个体编码长度不一而影响差分进化算子使用的问题。最后在三组UCI数据上的实验测试结果表明，本文算法具有良好的性能，其改进的寻优过程和集成操作对算法性能的提升均有显著作用。此外，算法中参数对性能影响的分析结果也揭示了其相应的设置规律。

［1］Handl J，Knowles J.An evolutionary approach to multiobjective clustering ［J］.IEEE Transactions on Evolutionary Computation，2007，11 （1）：56－76.

［2］Saha S，Bandyopadhyay S.A symmetry based multiobjective clustering technique for automatic evolution of clusters ［J］.Pattern Recognition，2010，43 （3）：738－751.

［3］ZHANG Huan，WANG Jinkun，CHEN Cheng.Research on the fault diagnosis of the excavator to be based on the multi－objective optimization clustering ［J］.Construction Machinery Technology ＆ Management，2013，26 （6）：115－117 （in Chinese）.［张欢，王锦锟，陈程.基于多目标优化聚类的挖掘机故障诊断研究 ［J］.建设机械技术与管理，2013，26 （6）：115－117.］

［4］QIN Liang，ZHANG Wenguang，SHI Xianjun，et al.Multi－objective clustering method based on immune clonal algorithm［J］.Information and Control，2013，42 （1）：8－12 （in Chinese）.［秦亮，张文广，史贤俊，等.基于免疫克隆算法的多目标聚类方法 ［J］.信息与控制，2013，42 （1）：8－12.］

［5］Qian Xiaoxue，Zhang Xianrong，Jiao Licheng，et al.Unsupervised texture image segmentation using multiobjective evolutionary clustering ensemble algorithm ［C］／／IEEE Congress on Evolutionary Computation.Piscataway，NJ，USA：IEEE，2008：3561－3567.

［6］Zhu Lin，Cao Longbing，Yang Jie.Multiobjective evolutionary algorithm－based soft subspace clustering ［C］／／IEEE Congress on Evolutionary Computation.NY，USA：IEEE，2012.

［7］LIN Jikeng，WANG Xudong，CHEN Yushan，et al.Distribution network reconfiguration based on feasible solution search and adaptive immune algorithm ［J］.Journal of Tianjin University （Science and Technology），2008，41 （12）：1505－1511（in Chinese）.［林济铿，王旭东，陈云山，等.基于可行解搜索和自适应免疫算法的配网重构 ［J］.天津大学学报，2008，41 （12）：1505－1511.］

［8］XUE Yu，ZHUANG Yi，MENG Xin，et al.Self－adaptive learning based ensemble algorithm for solving matrix eigenvalues［J］.Journal of Computer Research and Development，2013，50 （7）：1435－1443 （in Chinese）.［薛羽，庄毅，孟新，等.自适应学习集成优化算法及矩阵特征值求解 ［J］.计算机研究与发展，2013，50 （7）：1435－1443.］

［9］Strehl A，Ghosh J.Cluster ensembles：A knowledge reuse framework for combining multiple partitions ［J］.Journal of Machine Learning Research，2008，3 （3）：583－617.

［10］Deb K，Pratap A，Agarwal S，et al.A fast and elitist multiobjective genetic algorithm：NSGA－II ［J］.IEEE Transactions on Evolutionary Computation，2002，6 （2）：182－197.

［11］University of California，Irvine.UCI machine learning repository ［EB／OL］.［2013－09－20］.http：／／archive.ics.uci.edu／ml／datasets.html.

［12］WANG Junling，ZHOU Jianlin，BAO Fang，et al.Fuzzy C means clustering algorithm based on space distance of nearest pixels ［J］.Computer Engineering and Design，2013，34（7）：2476－2482 （in Chinese）.［王军玲，周建林，包芳，等.基于临近像素空间距离的模糊C均值聚类算法 ［J］.计算机工程与设计，2013，34 （7）：2476－2482.］

［13］MAO Guojun，CAO Yongcun.Clustering models and algorithms for distributed data streams based on data synopsis ［J］.Computer Science，2013，40 （6）：187－191 （in Chinese）.［毛国君，曹永存.基于数据概要描述的分布式数据流聚类模型与算法 ［J］.计算机科学，2013，40 （6）：187－191.］

［14］DENG Zelin，TAN Guanzheng，FAN Bishuang，et al.Effect of different distance measure methods on performance of artificial immune recognition system ［J］.Application Research of Computer，2011，28 （6）：2043－2045 （in Chinese）.［邓泽林，谭冠政，范必双，等.不同的距离测量方法对人工免疫识别系统的性能影响 ［J］.计算机应用研究，2011，28 （6）：2043－2045.］