CTCS3级列控系统ATP防护曲线算法研究

谭 莉，王长林

（西南交通大学 信息科学与技术学院，成都 610031）

列车超速防护（ATP，Automatic Train Protection）安全制动模型是列车自动防护系统的核心，直接影响着列车行车间隔、运输效率和行车安全。对ATP系统建模与ATP系统仿真实现的研究，从理论上，可以通过建立ATP系统模型，探索ATP系统的控车及防护机制。从实践上，可以及时发现设计疏漏，缩短新产品的研制周期，进行设备参数优化设计。因此，对基于通信的列车自动防护系统关键算法的研究具有重要意义。

1 ATP系统分析

ATP 系统是确保列车安全运行的关键，它由轨旁设备和车载设备组成。车载设备结构如图1所示，主要由ATP安全计算机（VC）、应答器信息接收模块（BTM）、轨道电路接收模块（STM）、制动接口单元、记录单元、人机界面（DMI）、速度传感器、BTM天线、STM天线等组成。

ATP车载设备根据地面设备提供的信号动态信息、线路静态参数、临时限速信息及有关动车组数据，生成控制速度和目标距离模式曲线，对列车行车安全进行防护，对安全设备或系统实行监控，实现超速防护、列车间隔控制、临时限速、列车定位、车门控制和后退防护等功能。记录单元对列控系统有关数据及操作状态实时动态记录。

图1 ATP车载设备系统结构

2 ATP速度防护模型

ATP防护曲线是根据列车制动性能、线路条件等因素采用列车牵引计算得到的。通过列车安全制动曲线，车载ATP 能够实时地监控列车的运行速度，保障列车的安全运行。在CTCS3级列控系统中，ATP防护曲线采用目标－距离模式，目标－距离模式曲线的算法基础就是列车安全制动距离的计算。在列车制动过程中，速度在连续变化，故列车制动合力也不断变化，即列车加速度也是连续变化的，因此采用取步长的办法进行计算。取步长的办法可分为时间步长、距离步长，速度步长。列车在整个制动过程中的制动加速度可表示为：

式（1）中：f为列车制动力（N/kN），w为列车单位基本阻力（N/kN），wi为单位坡道附加阻力（N/kN），wr为单位曲线附加阻力（N/kN），ws为单位隧道附加阻力（N/kN）。

因为轮对、电机等回转物体会消耗一部分动能，转动部分消耗的动能一般按列车功能的比例计算，该比例值称为回转质量系数γ。这样列车制动加速度修正为：

根据图2所示，取时间为步长的方法就是把整个列车制动的过程细分为若干个时间段∆t，在∆t时间内，列车速度恒定，由此列车的制动合力是一个常数。取其中一段∆t，根据运动学公式，可得在∆t时间内，列车的速度增量∆vi为：

图2 ATP安全制动曲线计算原理

列车的距离增量∆si为：

式（4）中：fi为列车在∆t时间内的制动力（N/kN），v初为列车制动初速度（m/s），v末为列车制动末速度（m/s），γ为回转质量系数。

然后将这些在∆t 时间内变化的位移∆si叠加，即可得到列车安全制动距离S：

而把所得到的∆si、∆vi连接起来则可得到V–S图，即目标－距离模式的ATP安全制动曲线。由于离散计算总是存在一定的误差，但是当 取足够小时，列车安全制动曲线的计算误差可控制在0.5%以内，能够达到工程要求。

由于列车在进行紧急制动时需要施加最大制动力，即列车从一开始就施加了空气制动，故车载ATP在计算列车紧急制动曲线（EBI）时需要考虑列车牵引切断、制动响应的时间，即空走时间。

列车的制动距离长度则为列车安全制动距离和列车空走距离之和，即：

式（6）中：v为列车制动起始速度（km/h），t空走为列车空走时间。

3 安全制动曲线步长选取的分析

列车超速防护曲线是按步长计算，不能恰好算到目标值处，设计时给出一个允许误差ξ，当列车速度值在误差ξ范围内，则等同列车速度已满足目标值vmax，即为迭代计算的终止条件。在列车安全制动距离的计算中，步长的选取办法可分为时间步长∆t，距离步长∆s，速度步长∆v。在计算过程中，选择不同参数的步长或者步长的长短取得不同，计算结果的精确度和收敛性都会是不同的。

3.1 变步长∆t法

在牵引计算中，通常选择∆t为步长，而为了提高计算结果的精度，采用变步长法进行计算，步长∆t取值通常为50 ms～1 000 ms 间，开始时速度比较小，步长取值较大，然后随着速度增大，步长逐渐缩小。如图3 所示，其中a为牵引加速度，f(∆t)为步长∆t的函数，随着速度大小的变化， ∆t将取不同的值。

根据流程图（如图3所示）分析，如果列车速度值在循环中跨过允许误差区间，就需要试凑函数缩小步长∆t，使得速度值可以被捕捉到。该方法的缺陷在于试凑需要将计算回滚，将不利于仿真帧稳定和时间同步。而定步长法中，往往将步长设计得非常小，如0.01 s，这样看似精确且不需要试凑，但是在列车运行的某些阶段，如以最大牵引力运行的牵引初始阶段，非常小的步长显然是没必要的； 其次，如果此时允许误差值取得不恰当，则列车是以接近允许误差的下限值在运行，实际上就是列车还没有达到最大值就开始准备制动了，这不利于提高运行效率。所以为了满足必要的精确度和运行效率的要求，需要根据列车运行速度的大小选取合适的步长。

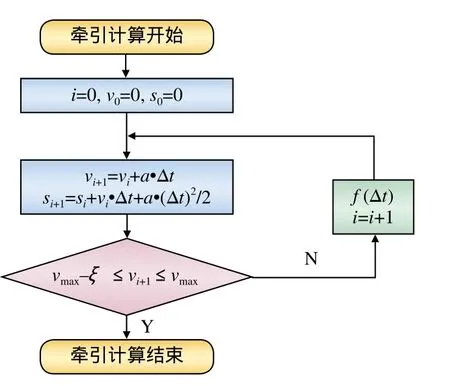
图3 牵引计算流程图

3.2 选取不同的步长∆ t ，∆ v ，∆ s法

以CRH3型动车组常规制动作为实例，假设在无坡度，无隧道和弯道的条件下，利用VC仿真计算，当列车接近停车点，取v=7.2 km/h时，a=0.6 m/s2，当列车接近制动点，取 v=300 km/h时，a=1.7 m/s2。

当选取时间为步长时，假设取∆t=0.5 s，根据运动学公式：∆v= ∆t•a，∆s=(v2末–v2初）/(2•a)可知：v=7.2 km/h时，计算得∆v=0.3 m/s， ∆s=1.1 m。v=300 km/h时，计算得 ∆v=0.85 m/s，∆s=41.7 m。

当选取速度为步长时，假设取∆v=3 m/s，根据运动学公式：∆t=∆v/a，∆s=(v2末–v2初）/(2•a)可知：v=7.2 km/h时，计算得∆t=5 s，∆s=17.5 m。v=300 km/h时，计算得∆t =1.76 s，∆s=147.1 m。

表1 不同步长参数下牵引计算的精度

比较3种取法的结果可知，选取时间为步长的方法，在停车点附近的计算精度较高，但是在制动点附近的计算精度比较差。选取速度为步长的方法，在加速度较大时计算精度较高，在停车点附近的精度较差，容易造成停车点不准确。而选取距离为步长时，在速度较大的情况下，计算精度较高。

考虑到在列车制动过程中，加速度a一般都小于2 m/s2，若选∆v为步长计算精度都不会太高，故本文中将选取∆t和∆s作为牵引计算的步长，在列车低速运行时选∆s为步长，在列车高速运行时选∆t为步长，这样既能满足必要的精度要求，又能提高函数的收敛性。

4 ATP防护曲线仿真算法原理

目标距离模式曲线的算法基础是列车安全制动距离计算。列车安全制动距离的计算涉及到列车牵引计算。由于ATP防护曲线的计算不涉及牵引工况，故牵引计算中只有制动力和阻力。其单位制动合力即为：

式（7）中，

c—列车的单位阻力（N/kN）；

w0—列车单位基本阻力（N/kN）；

wi—单位坡道附加阻力（N/kN）；

wr—单位曲线附加阻力（N/kN）；

ws—单位隧道附加阻力（N/kN）。

b—列车制动力（N/kN）；

制动加速度可表示为：

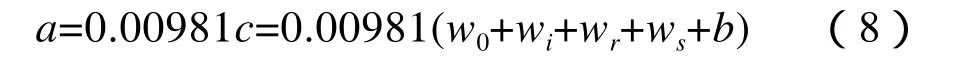
因为轮对、电机等回转物体会消耗一部分动能，转动部分消耗的动能一般按列车功能的比例计算，该比例值称为回转质量系数γ。修正后的制动加速度为：

目前超速防护曲线的电算方法主要有3种：反算法、直接计算法和双向递推算法。直接计算法最接近实际，但实现的步骤太繁琐，需要大量反复的迭代运算；双向递推法过程简单便于计算，但是需要作图找交点，如果用曲线拟和的方法太过复杂，但是用离散点组建数组，把求两曲线交点的问题转化为求两直线的交点，又可能精度不够。反算法结合了上述两种方法的特点，通过纯数学的手段，充分利用计算机处理重复运算快的特点，找到了接近实际、简单实用的计算方法。

反算法原理如图4所示，已知列车距目标停车点或减速点的距离，即目标距离为DT，在计算速度控制曲线时，可采用分段迭代法。将长度为DT的区段等分为n个长度为∆s的小区段，从已知目标点的目标速度向较高速度反方向计算。

图4 防护曲线反算法原理

从图4可知，从第n个∆s小区段开始，令该区段的制动末速度vt等于目标速度vT。若选∆s为步长，代入式，可算出该区段的制动初速度v0。令相邻的第（n–1）个∆s的制动末速度为第n个区段的制动初速度，计算出第（n–1）个区段的制动初速度，以此类推，当n取足够大的值时，速度点即形成一条光滑的速度曲线。当计算到某个小区段的制动初速度等于或大于最高限制速度vlim时，表明本点即为制动起点，制动起点到列车当前位置防护速度均为最好限制速度vlim。

根据前面关于步长选取的分析，在本模型中，选取∆t和∆s为步长。根据运动学公式，若选∆t为步长，则：

若选∆s为步长，则：

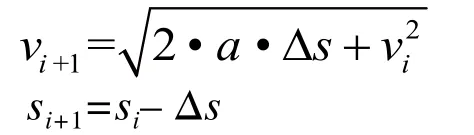
速度控制曲线仿真算法流程如图5所示。

图5 速度控制曲线仿真算法流程图

算法流程描述如下：

（1）根据接收的轨道电路信息，确定制动曲线的目标距离点DT和目标速度vT；

（2）令i=0，vi=vT，si=DT即确定制动曲线的初始速度和位移；

（3）根据位移和线路数据确定该位置的最具限制速度，确定本次计算的限速vlim；

（4）判断vi是否小于vlim，若vi＜vlim，再判断vi是否小于vts（vts为步长由∆t换成∆s的速度分界值），若vi≤vts，则vi+1=vi+a•∆s，si+1=si–(vi•∆t+a•(∆t)2/2)，若vi>vts，则si+1=si–∆s；

（5）若vi≥vlim，则vi+1=vlim，si+1=si–∆s；

（6）令i=i+1，判断i的大小，若i＜N，则返回步骤3，否则计算完成。

5 车载ATP曲线的仿真实现

5.1 ATP曲线仿真系统流程图

图6 ATP曲线仿真系统流程图

如图6所示，接收到的移动授权包括了目标点的位置和速度，然后利用前面讨论的分段迭代法，将目标距离分成N个小区段，从已知目标点的目标速度向较高速度反方向计算。在计算每个小区段的初速度和位置时，要先获得当前位置的最具限速度，比较当前速度与最具限速度的大小，若当前速度小于最具限速度，然后计算当前位置的加速度，再计算区段初速度和初位置。如当前速度大于最具限速度，则区段初速度等于最具限速度。如此循环，直到计算得到列车所在位置。

5.2 仿真线路参数和车辆参数

在ATP曲线仿真过程中，需要选择一定的线路参数，线路参数选择两站一区间，包括线路长度、坡道、弯道、隧道和最具限制速度等，具体参数见表2和表3。

表2 线路坡道、弯道、隧道的参数表

动车组的数据包括编组长度，质量（包括自重和定员重量）、单位阻力、回转惯量、牵引特性曲线和制动特性曲线等。CRH3型动车组主要参数如表4所示。

表4 CRH3型动车组参数表

5.3 列车运行阻力的仿真计算

列车运行过程中由于机械摩擦、空气摩擦、坡道、弯道等因素产生的与列车运行方向相反，阻碍列车运行的力叫做列车运行阻力。按照引起阻力的原因，可分为基本阻力和附加阻力。附加阻力又包括坡道附加阻力、曲线附加阻力和隧道附加阻力。

查资料可知，CRH3型动车组的单位重量基本阻力：

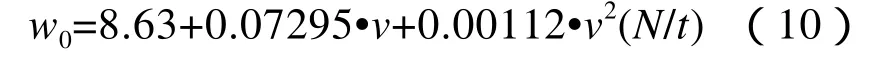
坡度附加阻力公式为：

式（12）～式（13）中，wr为单位重量曲线阻力(N/kN)，R为曲线半径(m)，ws为单位重量隧道附加阻力(N/kN)，Ls为隧道长度(m)。

5.4 ATP曲线仿真系统的仿真结果

仿真结果如图7～图9所示。

从图7可以看出，当线路上无临时限速时，ATP曲线从目标点反方向一直算到列车当前允许速度，然后保持该速度不变，一直到列车当前位置。紧急制动的加速度比常规制动的加速度大，所以紧急制动距离小于常规制动距离。

在有临时限速的条件下：由图8可知，当列车从高速度降为较低的速度时，依然要根据线路参数、列车性能等数据进行制动曲线的计算，此次制动的目标点为临时限速的起点，制动的目标速度为临时限速的大小，一直计算到列车当前最大允许速度，然后保持该速度不变到列车当前位置；由图9可知，当列车从低速度升为较高速度时，列车有一个施加牵引的过程，但在这个过程中列车的速度始终小于最大允许速度，所以防护曲线可以从较低的速度瞬间跳变到较高的速度，此时同样能够保证行车安全。

图7 无临时限速时的ATP曲线仿真图

图8 有临时限速时的ATP曲线仿真图（a）

图9 有临时限速时的ATP曲线仿真图（b）

6 结束语

本文从速度防护曲线生成的角度，研究了列车超速防护算法。讨论了ATP防护曲线仿真的主要算法，采用分段迭代法，并给出了该算法的软件设计流程和过程描述，便于软件仿真实现。在VC++6.0的软件平台上实现常规制动曲线和紧急制动曲线的仿真。解决了参数选取、制动力和阻力计算、线路限速等问题。对仿真结果进行了简要的分析，对解决ATP实际应用中出现的问题具有一定的参考意义。

[1]郭 宁.CTCS2级列控系统超速防护仿真研究[D].成都：西南交通大学，2008：43-44.

[2]谈 敏.CTCS3级车载设备测试平台研究[D].北京：北京交通大学，2008：5-9.

[3]张曙光. CTCS-3级列控系统总体技术方案[M]. 北京：中国铁道出版社，2008：2-3，92-105.

[4]王长林，林 颖. 列车运行控制技术[M]. 成都：西南交通大学出版社，2004：23-35.

[5]邓子渊. 城轨车载ATP系统的仿真设计与实现[J]. 铁道通信信号，2006（2）：42-43.