低碳经济背景下班轮航线配船

薛颖霞, 邵俊岗

(1.上海财经大学 浙江学院, 浙江 金华 321013; 2.上海海事大学 水运经济研究所， 上海 201306)

低碳经济背景下班轮航线配船

薛颖霞1, 邵俊岗2

(1.上海财经大学 浙江学院, 浙江 金华 321013; 2.上海海事大学 水运经济研究所， 上海 201306)

针对温室效应不断加剧、能源问题日益突出、低碳经济已经受到全世界广泛关注、严重的碳排放使航运业成为了低碳经济时代的焦点的现状,对低碳经济背景下的班轮航线配船进行研究。建立集装箱班轮航线配船的总成本最小化与碳排放量最小化的双目标规划模型，并通过MATLAB进行求解，得到合理的航线配船方案。该方案对班轮公司通过航线配船实现节能减排的目的具有重要的意义。

交通运输经济学;低碳经济；航线配船；碳排放最小化；成本最小化；双目标规划

随着全球能源价格不断上升、温室效应对全球环境的影响日益严重，走低碳发展之路正成为人们的共识。据统计，全球船舶每年二氧化碳排放量在12亿t左右，约占主要温室气体排放量的5%，预计到2020年，温室气体的排放量将在目前的基础上增加75%，航运业的低碳发展已经刻不容缓。相关研究结果表明，集装箱船的二氧化碳排放量约为大宗散货、邮船和件杂货船的1.3倍、2.2倍和2.5倍，因此， 集装箱运输方面的节能减排是一个值得思考的问题。

航线规划是一项十分复杂的工作，涉及因素众多。国内外很多学者对其进行了研究，并从不同角度提出了多种解决方案。RONEN[1]提出根据货运情况优化给定航线的船型。POWELL等[2]建立了求解各船舶挂靠顺序的混合整数规划模型。谢新连等[3]建立了以船队的营运和造船的总费用最小为目标函数的线性模型。苏绍娟[4]把船价、运价等营运参数作为随机、模糊函数，建立了基于不确定性的动态船队规划模型。杨秋平等[5]建立了以船队总营运利润最大为目标函数的、将船队短期调配使用与长期发展规划结合起来统筹分析研究的航线配船与船队规划数学模型。目前，关于低碳经济下的航运业的研究大多集中于船舶节能技术[6-8]、生物能源在船舶上的应用[9-10]、船舶航速与节能减排的关系[11-12]等方面。也有学者认为，船舶的大型化可以实现低碳、低成本运输。但是，购置大型新船需要巨额资金，会给船公司带来财务风险，而且，如果船公司普遍盲目扩大运力，会带来航运市场的恶性竞争，导致运价下跌。

当前航运市场正处于低迷期，运力普遍过剩，多数航运企业不会选择购置大型新船，因此，如何有效利用已有船舶资源显得尤为重要。此处从航线配船的角度研究如何通过航线配船来减少碳排放。

1 航线配船双目标规划模型的构建

1.1问题描述以及模型假设

以某班轮公司在某一时刻的状态为研究对象，已知该班轮公司未来一段时间的航线、船舶信息及运量的预测量，研究其在低碳经济背景下应该如何制定出合理的航线配船方案。

航线配船是一个动态、多变、复杂的工作，应用数学模型进行模拟存在一定难度，因此需对其做出适当的假设。模型的基本假设为

1) 该模型计划期为1 a。

2) 计划期内，该班轮公司不会有新的集装箱船交付，也不会有旧的集装箱船退出市场。

3) 各航线货流量预测较准确，且均匀发生。

4) 存在闲置船舶时，不考虑将其外租所带来的收益。

1.2变量说明

1.3模型关系构建

一般而言，航行成本主要包括固定费用(包括船舶及设备的折旧费、保险费、船员及管理人员工资等)、燃料费、港口费、运河费，其中燃料费是航行成本中最重要的一项，约占50%。近几年，随着原油价格不断走高，燃油成本所占比例再次提高，已高达50%～60%。

1.3.1船舶航速与船舶往返航次时间的关系

船舶往返航次时间为船舶航行时间与船舶靠港停泊时间之和，其表达式为

(1)

1.3.2年往返航次

设定年运营时间为350 d，年往返航次为

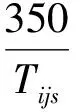
(2)

1.3.3航次燃料费用

航次燃料费用包括主机燃油费用和副机燃油费用2部分，主要考虑航行中的主机燃油费用与副机燃油费用。

1.3.3.1 主机燃油费用

船舶发动机实际功率与航速间的关系为

P=0.735 5×D2/3V3/C

(3)

(4)

式(4)中：fi为i型船舶的主机燃油单耗，kg/(kW·h)；Pi为i型船舶的主机实际功率，kW。

(5)

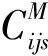
(6)

1.3.3.2 副机燃料油费用

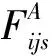
(7)

Horn 涡轮旋风切削可用于加工单线、多线螺纹和各种外形轮廓。而且，经过精密打磨的 S271 双刃可转位刀片是为不同的螺纹牙形和加工材料量身定制的。将可转位刀片安装在大小合适、高度稳定的刀片座内，刀片座既可以安装在新型模块化旋风铣刀头上，又可以直接安装在机床动力刀座上。

(8)

1.3.4单位往返航行成本

Cijs的计算公式为

(9)

1.3.5每个航次的碳排放量

能源碳排放因子是指消耗单位能源所生成的二氧化碳的量，利用各类能源的碳排放因子和能源消耗量可以对能源的碳排放量进行定量计算。因此，确定燃油的碳排放因子是研究低碳减排的基础。

此处所用碳排放因子依据国际海事组织对船舶运输中的碳排放因子的测定值。《IMO GHG Study of 2009》对船舶重油和轻油的碳排放因子进行了测定，分别为3.012和3.082。相关统计结果表明，在船舶的燃油消耗中，主机燃油约占87%，副机燃油约占11%，锅炉燃油约占2%。因此，所建模型只考虑主机的碳排放量，其计算公式可表示为

(10)

1.4航线配船双目标规划模型构建

1.4.1目标函数

在计划期内,同时追求集装箱班轮航线配船总营运成本最小和主机二氧化碳排放量最小；二氧化碳排放量主要根据式(10)进行计算，其值与燃油消耗有关。

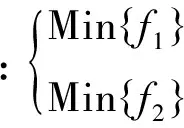
(11)

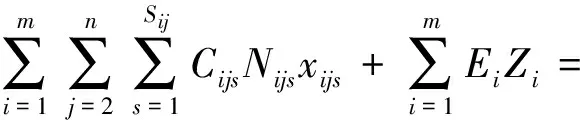
(12)

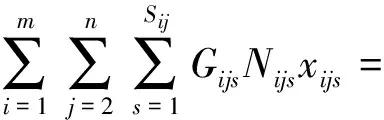
(13)

1.4.2约束函数

(14)

第1个约束函数式是对各集装箱船总数的约束；第2、第3个约束条件是对正向、反向最大装载率的约束;第4个约束条件是对船舶数量的非负性以及整数性的约束。所建模型中,对同一航线同种船型,可以根据需要选择不同的航速，这样的设计具有较高的灵活性，更有利于实现成本的最小化。后面将在算例中对这种改进的有效性进行验证。

2 双目标模型的转化

双目标模型一般通过2种方法求解：

1.化多为少，将其化为单目标模型。

2.分层序列法，按重要性对目标排序，在前一目标的最优解集内求下一目标的最优解，直至最后一个目标。

此处采用主要目标法将双目标模型转化成单目标模型。具体转化方法为：将f1作为主目标，不发生改变；设定碳排放量目标值K，将f2≤K加入约束函数，将双目标模型转化为单目标模型。在具体应用中,可以将K设定为某一具体数值，或将其设定为不同的值，对不同K所对应的航线配船方案进行比较，以选择最优方案。转化后的模型可以通过MATLAB进行求解，转化后的航线配船模型为

目标函数：f1

约束函数：

(15)

3 算例验证与分析

某公司拥有多条全集装箱班轮航线，经营多条集装箱航线，选取其中3条进行研究。船舶配置、各航线正向与反向运量预测，当前船舶、航速以及对应的航行成本见表1～表3。

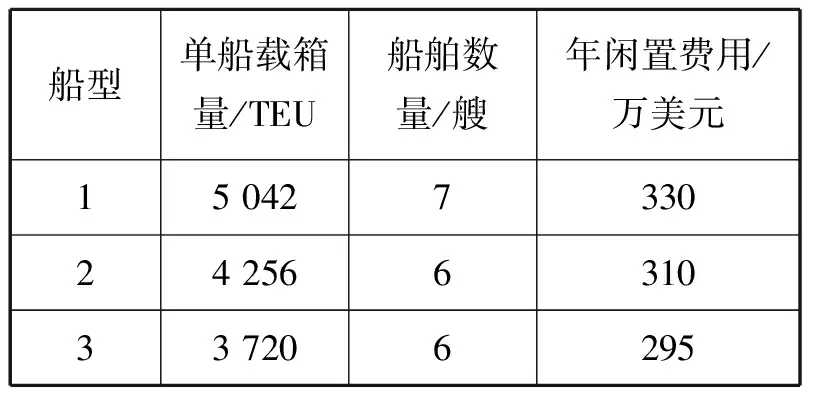
表1 船舶参数

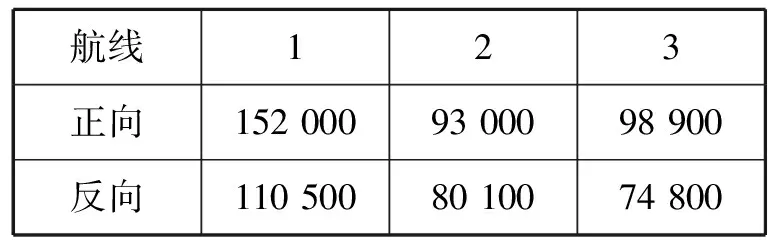
表2 各航线集装箱运量预测 TEU/a

表3 各船型在各航线上的当前航速以及对应的航行成本 万美元/航次

运用传统航线配船模型(同一航线、同种船舶、同一航速)得到的方案的总成本为24 384万美元，碳排放总量为94.23万t，共闲置2艘船舶。

根据该班轮公司的运营情况，对各航线的航速进行重新设计，即为每条航线加入另一种新航速。各航线的航速以及对应的成本见表4。

表4 重新设计的各船型在各航线上的航速以及相应的航行成本 万美元/航次

通过双目标模型,将这3条航线上的碳排放量降低至传统配船模型碳排放量(94.23万t)的一定比例ρ以下，不同的ρ对应不同的航线配船方案，通过对比选择最优方案。将ρ分别取值为98%,96%,94%,92%,99%,…,82%,80%。在ρ=80%时无解，由此可知ρ在取所有lt;80%的数值时，该模型无解。ρ=82%时，双目标模型对应具体配船方案见表5。

表5 新建模型航线配船方案

该方案所对应的总成本为22 803万美元，碳排放量为76.92万t，闲置船舶数目为0。与传统模型相比，该模型的总营运成本降低了8.48%，碳排放降低了18.37%。此外，该模型还减少了运力浪费，充分利用了现有船舶资源。与无碳约束模型(将双目标模型的碳约束去掉)所对应的航线配船方案相比，总营运成本的差距不足0.47%，这证明加入碳约束后的双目标模型仍具有较好的成本优势。

4 结 语

低碳航运是航运业发展的必然趋势，本文建立了集装箱班轮航线配船的总营运成本最小化与碳排放量最小化的双目标规划模型，并通过一个算例对该模型进行了验证，证明该模型可以在一定程度上实现总成本最小化与碳排放量最小化的双重目的，对班轮公司在低碳背景下如何设计航线配船方案具有重要的参考意义。

[1] RONEN D. Cargo Ships Routing and Scheduling: Survey of Models and Problems[J]. European Journal of Operational Research, 1983, 78(5): 46-49.

[2] POWELL B, PERAKIS A N. Fleet Deployment Optimization for Liner Shipping: An Integer Programming Model[J]. Maritime Policy and Management, 1997, 24: 183-192.

[3] 谢新连，李树范，纪单尚，等. 船队规划的线性模型研究与应用[J]. 中国造船, 1989(3): 59-66.

[4] 苏绍娟. 不确定动态船队规划的数学模型研究[J]. 中国航海, 2008, 31(2): 158-161.

[5] 杨秋平, 谢新连, 苏晨. 航线配船与船队规划模型及算法实现[J]. 中国航海, 2009, 32(1): 91-95.

[6] 徐学光. 迎接生态文明——船舶轻量化与节能减排[C]. 中国造船工程学会编. 造船学术委员会造船企业节能减排技术学术交流会论文集. 上海: 中国造船工程学会, 2009.

[7] 叶高文. 船舶节能新技术开发与应用研究[J]. 机电产品开发与创新, 2007,20(6): 106-107.

[8] 林安平, 余培文. 数种船舶节能技术性能分析[J]. 中外船舶科技, 2009(1): 21-23.

[9] Technology Roadmap Biofuels for Transport. International Energy Agency[R]. 2011.

[10] 吴新宪. 太阳能和风能在船舶上的应用分析[D]. 武汉：武汉理工大学, 2010.

[11] 陈宝忠, 傅爱庆, 孙永明. 船舶减速航行与主机减额输出节能技术的分析研究[J]. 中国航海, 2005(1): 82-86.

[12] 吴明益. 船舶减速节能与航速的选择[J]. 武汉交通管理干部学院学报, 1994(2): 64-70.

FleetDeploymentforLinerShippinginLow-CarbonEconomy

XUEYingxia1,SHAOJungang2

(1. Shanghai University of Finance amp; Economics Zhejiang College, Jinhua 321013, China; 2. Research Institute for Science of Water Transport Economy, Shanghai Maritime University, Shanghai 201306, China)

With the greenhouse effect and energy issues becoming increasingly prominent, low-carbon economy has attracted worldwide attention. Due to its severe carbon emissions, the shipping industry has become the focus of "low-carbon economy era" and been forced to take the way of low-carbon development. A dual objective programming model is established for fleet deployment of container liner shipping to achieve the object of minimizing the total cost and carbon emission, and to obtain the reasonable fleet deployment scheme by MATLAB. This study is of great importance for container liner companies to realize energy conservation and emission reduction.

traffic transport economics; low-carbon economy; fleet deployment; carbon emission minimization; cost minimization; dual objective programming

2014-07-16

河南省软科学研究计划项目(112400420045)

薛颖霞(1986—)，女，山西运城人，助教，从事港航管理研究。E-mail:xueyingxiadream@163.com

邵俊岗(1963—)，男，河南西华人，教授，从事港航管理研究。E-mail:jgshao@shmtu.edu.cn

1000-4653(2014)04-0115-05

F552;U692.3+3

A