受力模式对沥青混合料动态模量的影响

李 强，李国芬，王宏畅

（1.南京林业大学 土木工程学院，江苏 南京 210037；2.东南大学 交通学院，江苏 南京 210096）

动态模量是描述沥青混合料动态应力－应变响应的一个重要参数，能较为真实地反映出沥青路面的工作状态［1］，因此在国内外主要的沥青路面设计方法中被广泛地用作沥青混合料基本材料参数［2］及质量控制和检验指标［3］.

一般在进行沥青路面力学分析时，往往只引用沥青混合料在单一受力模式（多为单轴压缩）下的动态模量.然而，对于不同的路面病害形式，路面结构内关键位置处的力学响应存在很大的差异，忽视受力模式不同对动态模量的影响会直接在路面结构分析和厚度设计中产生较大的误差，因此，有必要对不同受力模式下沥青混合料动态模量进行对比分析.目前国内外学者对沥青混合料动态模量的研究主要集中于单轴压缩、三轴压缩、间接拉伸、半圆弯曲以及四点弯曲动态模量的研究［4－7］.本文通过4种不同受力模式下的动态模量试验对不同时温条件下3种常用沥青混合料的动态模量进行研究，分析了受力模式、围压、应变水平等因素对沥青混合料动态模量主曲线的影响.

1 试验

1.1 原材料及配合比设计

采用3种常用沥青混合料（AC－20C（AC－20级配＋普通沥青PG 64－22），AC－20M（AC－20级配＋SBS改性沥青PG 76－22），SMA－13C（SMA－13 级配＋普通沥青PG 64－22））进行室内动态模量试验.沥青混合料集料级配设计见表1.通过Superpave体积设计法确定3种混合料的最佳沥青用量（质量分数）分别为5.0%，5.0%和6.5%.

表1 沥青混合料集料级配设计Table 1 Design for aggregate gradations of asphalt mixtures

1.2 试验方法

采用半正弦荷载在5个温度水平（－10，5，20，35，50 ℃）和6 个荷载作用频率（25.0，10.0，5.0，1.0，0.5，0.1Hz）下分别进行单轴压缩、三轴压缩、间接拉伸和四点弯曲动态模量试验.为了减小试件损伤，采用从低温到高温、从高频到低频的试验顺序.每组试验条件下进行3个平行试验.

采用MTS材料试验系统进行单轴压缩、三轴压缩以及间接拉伸动态模量试验，试验试件通过旋转压实仪制备，其中单轴和三轴压缩（围压水平为100，200kPa）试验试件为φ100×150mm 的圆柱体试件，间接拉伸试验试件为φ150×50mm 的圆柱体试件.通过疲劳试验机在5个应变水平（200×10－6，400×10－6，600×10－6，800×10－6，1 000×10－6）下进行四点弯曲动态模量试验，试验试件采用长400.0mm、宽63.5mm、高50.0mm 的小梁试件.

2 动态模量主曲线构建方法

沥青混合料是一种典型的黏弹性材料，其力学性质对于温度和荷载作用时间具有明显的依赖性，而这种温度效应和时间效应可以相互转换.因此，在进行沥青混合料动态模量分析时，基于时间－温度等效原理，将在不同温度和荷载作用频率下的动态模量实测值进行平移，可以形成1条在某一参考温度下的光滑曲线，即动态模量主曲线［5］.通过构建沥青混合料动态模量主曲线，可以将一定时温条件内的动态模量试验结果扩展到更广泛的时温域内，用以预测实验室内无法测定的极端条件下的沥青混合料动态模量.沥青混合料动态模量（︱E＊︱）主曲线一般通过Sigmoidal数学模型来描述：

式中：δ，α，β，γ均为模型参数，其中，δ表征动态模量最小值，δ＋α表征动态模量最大值（Emax），β和γ 表征动态模量主曲线形状；fr为参考温度tr下的换算频率，由下式计算：

式中：f 为某试验温度t 下的实际荷载作用频率；at为某试验温度t下动态模量主曲线移位因子.

分别采用2种常用的模型——Williams－Lardel－Fesry模型（WLF 模型，式（3））和Arrhenius模型（式（4））［8］计算移位因子，然后采用式（1）对动态模量试验数值进行拟合，构建动态模量主曲线，见图1.

式中：c1，c2均为模型参数；ΔE 为流体的活化能；R为理想气体常数.

图1 动态模量主曲线的构建Fig.1 Development of master curves for dynamic modulus

从图1中可以发现：（1）沥青混合料动态模量随着换算频率的降低（温度升高或荷载作用频率降低）而降低.这是因为在高温或荷载长期作用下，沥青混合料呈现出明显的黏弹特性，沥青材料逐渐软化，集料内摩阻力逐渐减小，造成混合料的抗变形能力逐渐劣化.（2）沥青混合料动态模量主曲线两端（高温低频段、低温高频段）趋向水平，表明混合料动态模量存在极大值和极小值.（3）基于2种移位因子计算模型建立的主曲线均可以很好地拟合混合料动态模量试验结果，但是当把主曲线向上、向下外延时可以发现，基于WLF 模型建立的动态模量主曲线明显高于基于Arrhenius模型建立的动态模量主曲线，这表明动态模量极值的预估结果依赖于移位因子的计算模型.其原因可能为WLF 模型只适用于玻璃态转移点tg～tg＋100℃左右的温度范围，而Arrhenius模型在低于软化点的温度下有效［8］.因此，为了解决上述问题，本文对动态模量主曲线的构建方法进行了改进，具体步骤如下：

（1）分别采用WLF和Arrhenius模型计算移位因子，通过Sigmoidal模型对动态模量试验数据进行第1次拟合，建立初始主曲线；

（2）采用基于WLF 模型的主曲线预估动态模量极大值，采用基于Arrhenius模型的主曲线预估动态模量极小值；

（3）以第（2）步预估得到的动态模量极大值和极小值作为已知点，采用任一移位因子计算模型（WLF或Arrhenius模型）和Sigmoidal模型对动态模量试验数据进行第2次拟合，建立最终主曲线.

由图1可以看出，无论采用哪种移位因子计算模型，2次拟合后得到的动态模量主曲线基本一致，即移位因子计算模式对动态模量主曲线的影响基本被消除.由图1 还可以看出，2 次拟合主曲线上的动态模量极大值与Hirsch模型预测结果基本一致［6］.

3 试验结果分析

采用改进后的动态模量主曲线构建方法（二次拟合时采用WLF模型）分别构建参考温度为20℃的沥青混合料单轴压缩（UC）、三轴压缩（TC）、间接拉伸（IDT）、四点弯曲（4PB）动态模量主曲线，结果见图2.依据动态模量主曲线换算频率（fr），采用WLF模型进行二次回归，得到c1，c2，然后绘制沥青混合料移位因子曲线，见图3.动态模量主曲线和移位因子模型参数见表2.

图2 不同受力模式下的动态模量主曲线Fig.2 Master curves of dynamic modulus under different loading modes

3.1 受力模式的影响

由图2可见，任一种沥青混合料的单轴压缩、间接拉伸和四点弯曲动态模量主曲线形状相近，即随温度和荷载作用频率的变化单轴压缩、间接拉伸和四点弯曲动态模量主曲线变化基本保持一致.在换算频率相同时，不同受力模式下的动态模量大小顺序为：单轴压缩动态模量＞间接拉伸动态模量＞四点弯曲动态模量，在低温高频段动态模量差别更为明显.这是因为在单轴压缩试验中，沥青与级配良好的集料共同承担荷载，集料骨架可以充分发挥嵌挤作用，因此混合料表现出较好的抗变形能力，具有较高的动态模量；在间接拉伸（劈裂）和四点弯曲状态下，混合料更多依靠沥青与集料的黏结力抵抗荷载，抗变形能力主要依赖于沥青胶结料，因此其动态模量较低［5］.另外，由于单轴压缩试验试件处于单轴应力状态而间接拉伸试验和四点弯曲试验试件处于两轴应力状态，试件成型过程中形成的材料各向异性也引起了上述差别.在同一换算频率下3种不同类型沥青混合料动态模量的差别不是太大，尤其是在高温低频段，这表明了采用动态模量参数不能很好地评价不同类型沥青混合料的高温稳定性［9］.

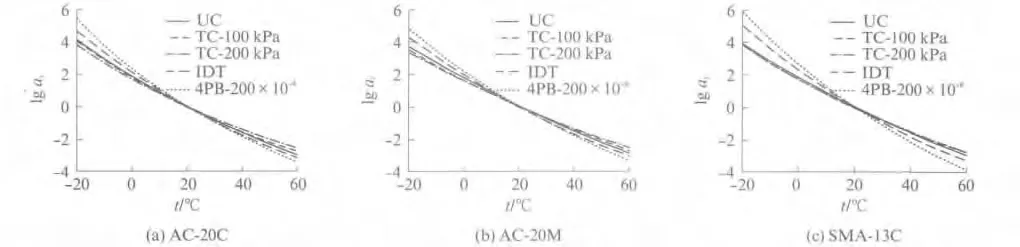
图3 不同受力模式下的移位因子曲线Fig.3 Shift factor curves under different loading modes

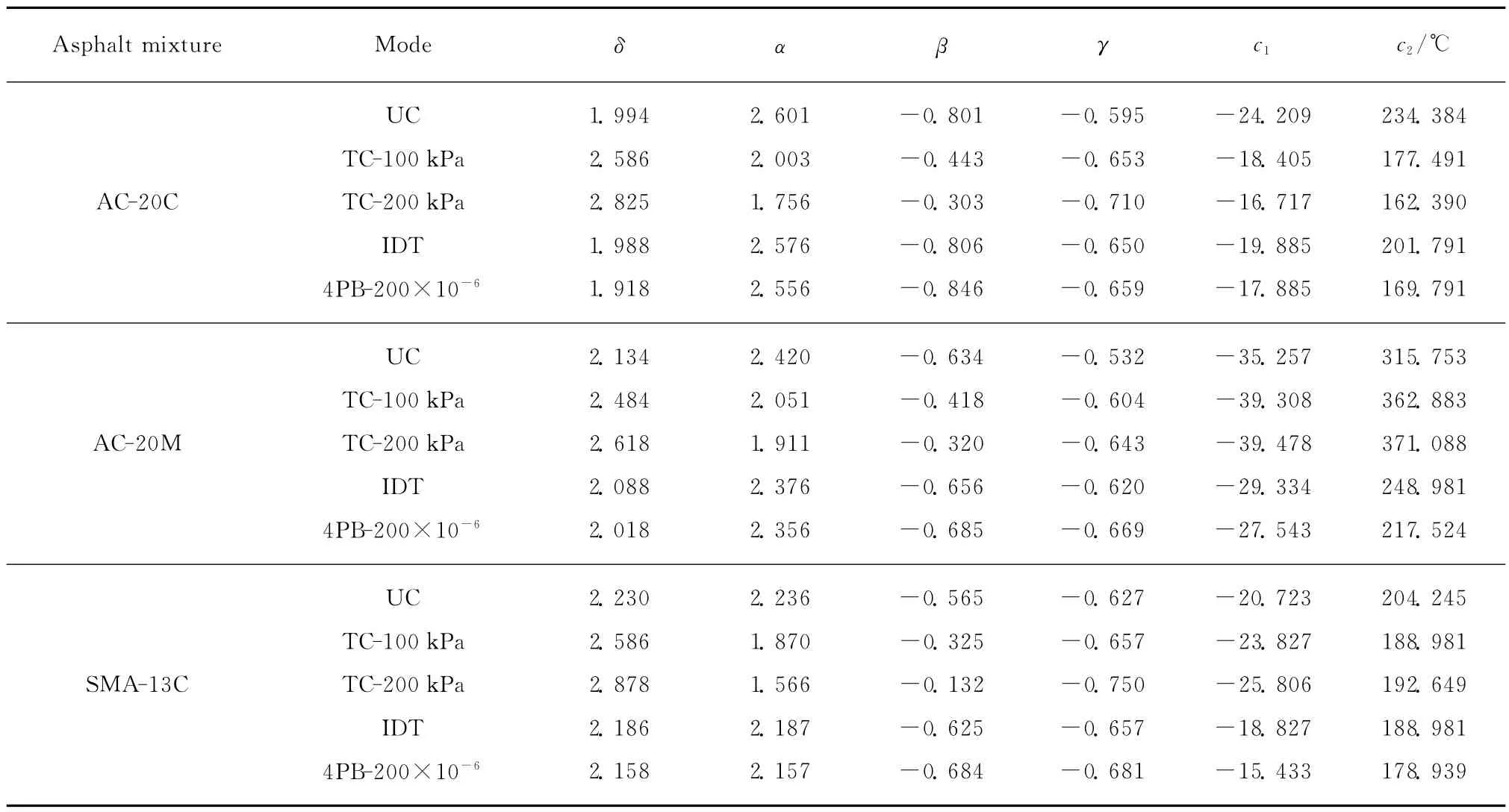
表2 主曲线和移位因子模型参数Table 2 Model coefficients of master curve and shift factor

对单轴压缩、间接拉伸和四点弯曲动态模量试验数据进行统计学分析，结果如表3所示.由表3可见，3种沥青混合料的t检验P 值均小于0.05，F 检验F 值均大于Fcritical，表明在95%的保证率下，3种沥青混合料单轴压缩、间接拉伸和四点弯曲动态模量均有显著区别.

从图3中发现，四点弯曲和间接拉伸模式下沥青混合料动态模量主曲线移位因子绝对值均明显大于单轴压缩模式下沥青混合料动态模量主曲线移位因子绝对值，表明在拉伸状态下混合料的温度敏感性较大.这是因为沥青混合料的温度敏感性主要依赖于沥青胶结料，而在拉伸状态下沥青胶结料对混合料抗变形能力的贡献比集料大，尤其在由高含量粗集料组成骨架结构的SMA－13C混合料中表现得更为显著.另外，采用SBS改性沥青的AC－20M 混合料的温度敏感性要小于另外2种采用普通沥青的混合料，这是由沥青胶结料自身性质决定的.

表3 统计学分析结果Table 3 Results of statistical analysis

通过回归分析得到了沥青混合料单轴压缩、间接拉伸和四点弯曲动态模量三者之间的拟合关系（适用于不同温度和荷载作用频率），如表4所示.由表4可见，所有拟合关系的R2均大于0.98，表明三者之间存在较好的相关关系.

表4 不同受力模式下动态模量之间的拟合关系Table 4 Fitting relationships of dynamic modulus under different loading modes

3.2 围压的影响

围压水平对沥青混合料动态模量的影响见图2.由图2可见，在低温高频段，围压对混合料动态模量几乎没有影响.随着温度的升高或者荷载作用频率的降低，围压的影响越来越显著，混合料动态模量随着围压的增大而增大.以AC－20C 混合料为例，在高温低频段围压水平为100kPa时混合料动态模量最高可达到无围压时的3.7 倍，而围压水平为200kPa时混合料动态模量最高能达到无围压时的6.4倍.这是因为在高温低频条件下，集料对混合料的抗变形能力起主导作用，围压越大，集料嵌挤越好，混合料动态模量越大［10］.另外，三轴压缩动态模量主曲线移位因子绝对值较单轴压缩动态模量主曲线移位因子绝对值小（如图3所示），表明围压的存在会降低混合料的温度敏感性.因此，为了更好地模拟沥青路面的实际受力状态，在进行路面力学分析时有必要考虑围压对材料动态模量的影响，以减小计算误差.为了描述沥青混合料动态模量的时温依赖性，采用Fillers－Moonan－Tschoegl（FMT）模型［11］综合考虑围压（p）和温度对移位因子的影响.需要注意的是当p 为基准围压p0（p0＝0）时，FMT 模型即为式（3）所示的WLF模型.

式中：C1，C4，A2，A3，B2，B3为模型参数，由非线性最小二乘法拟合不同围压水平下的动态模量试验数据而得，见表5.

表5 FMT模型参数Table 5 Parameters for FMT model

另外，考虑围压的影响［12］，对Sigmoidal动态模量模型进行改进：

式中：动态模量极大值Emax可以通过Hirsch 模型进行预估；ps为标准大气压；θ 为体积应力，等于3个主应力值之和；k1，k2，k3为模型参数.

从式（9）和式（10）中可以看出，围压对动态模量的影响主要通过体积应力θ对δ 的影响来体现.

同样，通过非线性最小二乘法对3种沥青混合料在不同围压水平下的动态模量试验数据进行拟合，得到改进Sigmoidal模型参数，见表6.

表6 改进Sigmoidal模型参数Table 6 Parameters for improved Sigmoidal model

3.3 应变水平的影响

在20℃，10Hz时沥青混合料四点弯曲动态模量与应变水平的关系如图4所示.从图4中可以看出：（1）沥青混合料四点弯曲动态模量与应变水平之间存在很好的指数函数关系，应变水平越高，混合料四点弯曲动态模量越小.这是因为四点弯曲试验采用的是应变控制模式，随着应变水平的提高，沥青混合料应力不断增大，其内部逐渐出现损伤破坏，形成微裂纹，导致动态模量降低.（2）采用SBS改性沥青的AC－20M 混合料四点弯曲动态模量受应变水平的影响明显小于另外2种混合料.

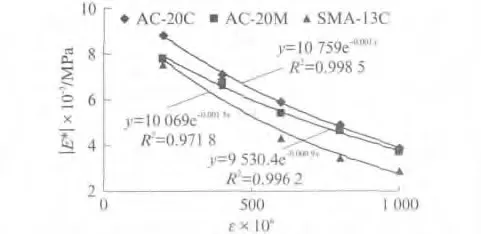
图4 沥青混合料四点弯曲动态模量与应变水平的关系Fig.4 Relationships between 4PB dynamic modulus and strain level

沥青混合料动态模量对于应变水平变化较为敏感.因此，在分析受力模式对混合料动态模量的影响时，为了与其他试验状态保持一致，仅列出了小应变水平（200×10－6）下的研究结果.另外，大量研究［13］表明，时间－温度等效原理在非线性及破坏阶段依然成立，因此仍可采用基于时间－温度等效原理的主曲线法来综合分析大应变水平下温度和荷载作用频率对沥青混合料动态模量的影响.

4 结论

（1）基于不同移位因子模型建立的沥青混合料动态模量主曲线均可以很好拟合混合料动态模量试验结果，但是主曲线上动态模量极值的预估结果依赖于移位因子计算模型.采用二次拟合可以消除不同移位因子计算模型的影响，建立基本一致的沥青混合料动态模量主曲线.

（2）在相同计算频率下，沥青混合料单轴压缩、间接拉伸和四点弯曲动态模量有差别，在低温高频段更明显，但三者之间存在较好的线性关系.在拉伸模式（间接拉伸和四点弯曲模式）下沥青混合料动态模量的温度敏感性较大，表现为其移位因子绝对值明显大于单轴压缩模式移位因子绝对值.另外，采用SBS改性沥青的AC－20M 混合料的温度敏感性要小于另外2 种采用普通沥青的AC－20C 和SMA－13C混合料.

（3）在低温高频段，围压对沥青混合料三轴压缩动态模量几乎没有影响；随着温度的升高或者荷载作用频率的降低，围压的影响越来越显著.围压的存在会降低混合料的温度敏感性.通过FMT 模型和改进Sigmoidal模型可分别建立沥青混合料移位因子－围压和动态模量－围压之间的函数关系式.

（4）在四点弯曲模式下沥青混合料动态模量对应变水平变化较为敏感.沥青混合料四点弯曲动态模量与应变水平之间存在很好的指数函数关系，应变水平越高，混合料四点弯曲动态模量越小，使用普通沥青时更为明显.

［1］韦金城，崔世萍，胡家波.沥青混合料动态模量试验研究［J］.建筑材料学报，2008，11（6）：657－661.WEI Jincheng，CUI Shiping，HU Jiabo.Research on dynamic modulus of asphalt mixtures［J］.Journal of Building Materials，2008，11（6）：657－661.（in Chinese）

［2］罗桑，钱振东，HARVEY J.环氧沥青混合料动态模量及其主曲线研究［J］.中国公路学报，2010，23（6）：16－20.LUO Sang，QIAN Zhendong，HARVEY J.Research on dynamic modulus for epoxy asphalt mixtures and its master curve［J］.China Journal of Highway and Transport，2010，23（6）：16－20.（in Chinese）

［3］WITCZAK M W，KALOUSH K，PELLINEN T，et al.National cooperative highway research program report 465：Simple performance test for superpave mix design［R］.Washington，D.C.：Transportation Research Board，2002.

［4］姚波，程刚，王晓.基于弯曲试验模式的环氧沥青混合料动态模量［J］.东南大学学报：自然科学版，2011，41（3）：597－600.YAO Bo，CHENG Gang，WANG Xiao.Dynamic modulus of epoxy asphalt mixture based on bending test mode［J］.Journal of Southeast University：Natural Science，2011，41（3）：597－600.（in Chinese）

［5］刘宇.基于半圆弯曲试验的沥青混合料动态响应及断裂性能研究［D］.哈尔滨：哈尔滨工业大学，2009.LIU Yu.Research on dynamic response and fracture performance of asphalt mixture based on semi－circular bending test［D］.Harbin：Harbin Institute of Technology，2009.（in Chinese）

［6］马林，张肖宁，陈少幸.基于间接拉伸试验模式的沥青混合料动态模量［J］.华南理工大学学报：自然科学版，2008，36（10）：86－91.MA Lin，ZHANG Xiaoning，CHEN Shaoxing.Dynamic modulus of asphalt mixtures based on indirect tensile mode［J］.Journal of South China University of Technology：Natural Science，2008，36（10）：86－91.（in Chinese）

［7］UNDERWOOD S B，KIM R Y.Viscoelastoplastic continuum damage model for asphalt concrete in tension［J］.Journal of Engineering Mechanics，2011，137（11）：732－739.

［8］张肖宁.沥青与沥青混合料的粘弹力学原理及应用［M］.北京：人民交通出版社，2006：79－81.ZHANG Xiaoning.Principles and application of viscoelasticity for asphalt and mixtures［M］.Beijing：China Communications Press，2006：79－81.（in Chinese）

［9］LI Q，NI F，LI G，et al.Evaluation of the dynamic modulus for asphalt mixtures with varying volumetric properties［J］.International Journal of Pavement Research and Technology，2013，6（3）：197－204.

［10］马翔，倪富健，陈荣生.沥青混合料动态模量试验及模型预估［J］.中国公路学报，2008，21（3）：35－39.MA Xiang，NI Fujian，CHEN Rongsheng.Dynamic modulus test of asphalt mixture and prediction model［J］.China Journal of Highway and Transport，2008，21（3）：35－39.（in Chinese）

［11］UZAN J.Permanent deformation in flexible pavements［J］.Journal of Transportation Engineering，2004，130（1）：6－13.

［12］赵延庆，叶勤，文健.围压对沥青混合料动态模量的影响［J］.重庆交通大学学报：自然科学版，2007，26（6）：96－99.ZHAO Yanqing，YE Qin，WEN Jian.Effects of confining pressure on dynamic modulus［J］.Journal of Chongqing Jiaotong University：Natural Science，2007，26（6）：96－99.（in Chinese）

［13］WU J W，COLLOP A C，MCDOWELL G R.Discrete element modeling of constant strain rate compression tests on idealized asphalt mixture［J］.Journal of Materials in Civil Engineering，2011，23（1）：2－11.