CRTSⅠ型CA砂浆动态受压损伤试验

徐 浩，王 平，魏贤奎，曾晓辉

（1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2.西南交通大学 土木工程学院，四川 成都 610031）

随着无砟轨道技术的日趋成熟和完善，世界各国高速铁路采用无砟轨道已成为主要的发展方向［1］.CRTSⅠ型板式无砟轨道是一种应用最多、最为成熟的无砟轨道结构型式［2］，由钢轨、扣件、轨道板、水泥乳化沥青砂浆（CA 砂浆）充填层以及混凝土底座板等组成.其中CA 砂浆是一种由水泥、乳化沥青、细骨料、水及铝粉等组成的有机－无机复合材料［3］，是填充于板式无砟轨道的轨道板与混凝土底座板之间的关键功能材料之一，起支承、调整、传载、减振和隔振等作用［4－8］.CRTSⅠ型板式无砟轨道CA 砂浆具有高韧性、低弹性模量和低强度的特点［3］.由于CA 砂浆是典型的黏弹性材料，其力学性能与外界荷载的作用时间及频率有关.

在CRTSⅠ型板式无砟轨道结构中，CA 砂浆主要承受列车的竖向荷载作用，且在列车行驶过程中CA 砂浆处于动态加载的状态［9－10］.列车运营速度变化将导致CA 砂浆应变率的变化，因此需要研究CA砂浆在不同应变率下的动态力学特性及损伤特性.国内外学者研究了不同加载速率对CA 砂浆力学性能的影响规律：文献［11］认为CA 砂浆的抗压强度随加载速率的增大而增大，二者大致呈线性关系；文献［12］针对2种典型的CA 砂浆进行不同加载速率下的抗压试验，结果表明这2种典型的CA 砂浆的峰值应力和弹性模量均随加载速率的增大而呈递增趋势，且加载速率对沥青与水泥质量比（mA／mC）较高的CA 砂浆影响更大；文献［13］认为CA 砂浆的抗压强度及弹性模量均随加载速率的增大而呈幂指数增大.虽然对不同加载速率下CA 砂浆的力学性能已经有了一定的研究，但所用试件均为实验室模制试件，由于现场环境复杂，养护、施工条件以及灌注袋的约束作用均会导致现场CA 砂浆与室内试件存在差异，因此模制试件无法真实反映现场CA 砂浆的动态力学性能.

本文对正在施工的某线上CRTSⅠ型板式无砟轨道进行现场揭板，并对揭板后的CA 砂浆层进行室内钻芯取样，测试不同应变率下现场取样CA 砂浆试件的应力－应变曲线，研究不同应变率对其抗压特性的影响；并以切线模量的退化来度量试件的损伤程度，研究了不同应变率下CA 砂浆的损伤槛值.

1 试验

1.1 试件制备

为了反映实际运营中的CRTSⅠ型板式无砟轨道CA 砂浆的力学性能，对正在施工的某线上CRTSⅠ型板式无砟轨道进行揭板，得到的CA 砂浆层未经历过动车荷载，对其在室内钻心取样，并加工成φ50×50mm 的圆柱体试件.现场取样CA 砂浆试件的原材料均来自安徽中铁工程材料科技有限公司，其干料24h体积膨胀率为2.1%，7d线膨胀率为0.1%，1d抗压强度为6.89MPa；改性阳离子乳化沥青固含量1）文中涉及的固含量、配合比等除特别说明外均为质量分数或质量比.为62.1%.现场取样CA 砂浆试件的配合比m（干料）∶m（乳化沥青）∶m（水）∶m（减水剂）∶m（引气剂）∶m（消泡剂）＝（900～1 150）∶（400～550）∶（30～100）∶（0.5～5.0）∶（1～5）∶（0.05～0.50）.新拌CA 砂浆的J型漏斗流下时间为24s，分离度为0.2%.硬化CA 砂浆的1d抗压强度为0.5MPa，28d抗压强度为2.0MPa.现场取样CA 砂浆试件的各项性能均满足《客运专线铁路CRTSⅠ型板式无砟轨道水泥乳化沥青砂浆暂行技术条件》.

1.2 力学性能测试

采用WDW 系列微机控制电子万能试验机对现场取样CA 砂浆试件进行动态单轴抗压试验，试验方法参照文献［13］进行.综合考虑试验系统的加载能力，加载速率确定为0.03，0.30，3.00，30.00mm／min，根据CA 砂浆试件尺寸对应的应变率Δε为1×10－5～1×10－2s－1，取1×10－5s－1作为准静态应变率.每组加载试验取3 个试件，编号为CA1～CA3.若试验结果离散性较大，则增加试件数量以保证试验数据的有效性.试件受压面与加载板之间采用滑石粉进行减摩处理.为防止试件表面不平整产生的误差，正式加载前将试件以0.5mm／min的速率、0.05 MPa的强度预压3 次.加载时由于仪器或测试的原因致使应力－应变曲线中0～0.25 MPa范围内应力变化缓慢（见图1中AB 段），按文献［13］的方法进行数据处理，即从B 点作切线，以切线与横坐标的交点C 作为修正后的原点.以应力－应变曲线最高点的横、纵坐标作为CA 砂浆峰值应力处的应变（临界应变εc）和抗压强度σc.

2 试验结果分析

2.1 CA 砂浆应力－应变曲线

图1 CA 砂浆应力－应变曲线Fig.1 σ－εcurve of CA mortar（Δε＝1×10－4s－1）

图2 不同应变率下CA 砂浆应力－应变曲线Fig.2 σ－εcurves of CA mortar under different strain rates

应力－应变（σ－ε）曲线能够全面体现CA 砂浆在加载过程中的力学性能，是进行其他力学分析的基础.不同应变率（Δε）下CA 砂浆的应力－应变曲线如图2所示.由图2可见，不同应变率下CA 砂浆的应力－应变曲线形状基本一致，其应力在达到峰值后降低较为缓慢，这是由于沥青的存在改善了CA 砂浆的断裂韧性.当CA 砂浆的应变达到0.08时仍具有一定的承载能力，说明其具有良好的韧性和延展性.CA 砂浆的抗压强度和临界应变均随着应变率的增大而增大，当应变率从1×10－5s－1增至1×10－2s－1时，该CA 砂浆的抗压强度由2.221 MPa 增至5.189MPa，同时临界应变由0.017 58增至0.023 75.

2.2 CA 砂浆的抗压强度

抗压强度是描述CA 砂浆力学性能的重要参数.根据试验测得的应力－应变曲线数据，得到不同应变率下CA 砂浆的抗压强度σc，列于表1.由表1可知，CA 砂浆试件的抗压强度在同一应变率下表现出不等的离散性，这是由于试验不可避免的误差造成的.本试验以应变率为1×10－5s－1时的抗压强度作为CA 砂浆的准静态抗压强度，当应变率分别为1×10－4，1×10－3，1×10－2s－1时，CA 砂浆的抗压强度分别增长了22.657%，62.331%，149.417%.CA 砂浆的抗压强度随着应变率的增大而增加，原因是CA 砂浆破坏时不再按原来的微裂缝路径发展，而是沿耗能最快的路径发展，因此其抗压强度逐渐增大.

根据文献［13］的研究可知，CA 砂浆的抗压强度随应变率呈幂函数变化，两者的关系可表示为y＝axb.本文考虑到幂函数还可以表示为y＝a＋bxc（式中：y 代表CA 砂浆在不同应变率下的抗压强度；x 代表应变率；a，b，c为拟合曲线系数），因此按这2种幂函数关系式拟合CA 砂浆抗压强度与应变率的关系，得到的拟合曲线如图3所示.

表1 不同应变率下CA砂浆的抗压强度σcTable 1 Compressive strength of CA mortar under different strain rates MPa

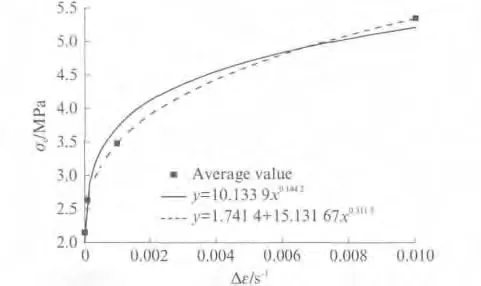
图3 CA 砂浆抗压强度与应变率的关系Fig.3 Relationship between compressive strength of CA mortar and strain rate

不同的幂函数拟合得到的CA 砂浆的抗压强度与应变率之间的关系式分别为y＝10.133 9x0.1442，拟合优度R2＝0.977 1；y＝1.741 4＋15.131 7x0.3115，拟合优度R2＝0.999 7.从拟合优度可知，采用幂函数y＝a＋bxc来拟合CA 砂浆抗压强度与应变率的关系更优.

2.3 CA 砂浆的弹性模量

弹性模量是描述CA 砂浆力学性能的又一重要参数，且随着应变率的增加而增加［11－13］.为了定量描述弹性模量与应变率的关系，本文采用0～1／3抗压强度处的割线模量作为CA 砂浆的弹性模量Ec［13］.不同应变率下CA 砂浆的弹性模量如表2所示.

图4为CA 砂浆的弹性模量与应变率的关系图.由图4可知，CA 砂浆的弹性模量随应变率的增加呈幂函数增大，关系式为：y＝110＋748.043 3x0.1663，拟合优度R2＝0.999 1，其中y 代表CA 砂浆的弹性模量.

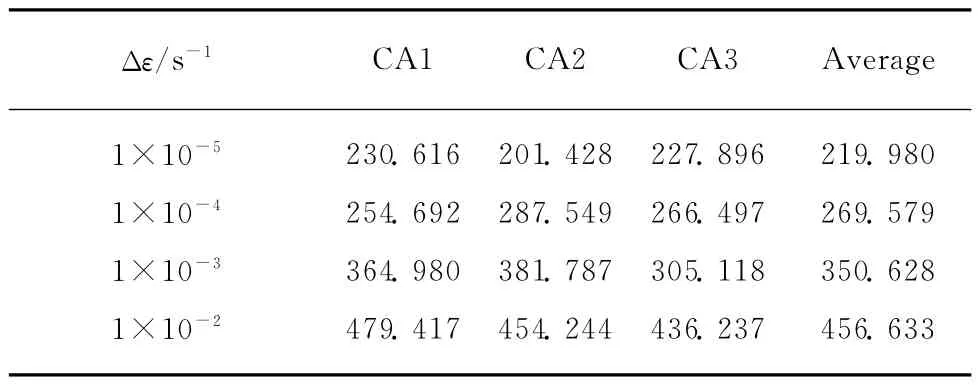
表2 不同应变率下的CA砂浆的弹性模量EcTable 2 Elastic modulus of CA mortar under different strain rates MPa

图4 CA 砂浆弹性模量与应变率的关系Fig.4 Relationship between elastic modulus of CA mortar and strain rate

2.4 CA 砂浆的临界应变

临界应变定义为CA 砂浆峰值应力处的应变，是反映CA 砂浆变形特性的重要参数之一.在本试验中，发现随着应变率的增加，CA 砂浆的临界应变增大，不同应变率下CA 砂浆的临界应变εc见表3.

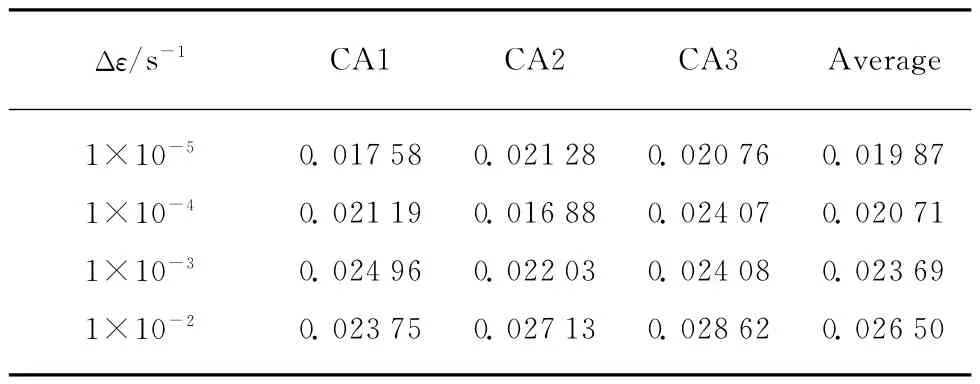
表3 不同应变率下CA砂浆的临界应变εcTable 3 Critical strain of CA mortar under different strain rates

在动荷载作用下，CA 砂浆的临界应变是由CA砂浆的弹性应变和黏性应变共同引起的.随着应变率的增加，沥青的掺入使得CA 砂浆的黏性表现得更明显，其黏性应变效应增加，因而导致CA 砂浆在峰值应力处的应变增加.图5给出了CA 砂浆的临界应变与应变率的关系.由图5可知，CA 砂浆临界应变也随应变率的增加呈幂函数增大，关系式为：y＝0.016 61＋0.021 89x0.1705，拟合优度R2＝0.960 3，其中y 代表CA 砂浆的临界应变.

图5 CA 砂浆的临界应变与应变率的关系Fig.5 Relationship between critical strain of CA mortar and strain rate

3 CA砂浆动态损伤特性分析

当加载到相同的应变时，不同应变率下CA 砂浆的破坏情况如图6所示.由图6可见，CA 砂浆的破坏情况在低应变率下较高应变率下更为严重.当应变率为1×10－5s－1时，CA 砂浆试件不仅严重开裂还出现掉块现象；而当应变率增大到1×10－2s－1时，CA 砂浆试件仅出现少量开裂.这是因为CA 砂浆属于典型的黏弹性材料，在动态荷载作用下其应力和应变存在滞后效应［14］，应变率越小，作用时间越长，CA 砂浆的变形越充分，其破坏情况也越严重.

图6 不同应变率下CA 砂浆的破坏情况Fig.6 Damage state of CA mortars under different strain rates

本文从宏观上定义CA 砂浆的损伤程度D，即用CA 砂浆试件受损伤而引起的宏观力学性能参数的变化量（切线模量的退化）来表征CA 砂浆的损伤程度，即：

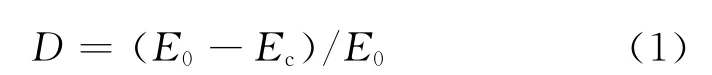
式中：E0指初始切线模量；Ec指任一应力水平比对应的切线模量，其中应力水平比指不同应变率下CA 砂浆应力－应变曲线上升段中任一应力与相应抗压强度的比值.使用该方法可以不计CA 砂浆的初始微裂隙和微空洞，能简化CA 砂浆内部损伤生成和演化的测量过程，从而对CA 砂浆在动态受压情况下的实时损伤演化规律进行分析和研究.本文参考文献［15］，引入描述混凝土损伤程度的方法及“应力空间”和“应变空间”的概念来描述CA 砂浆在不同应变率下的动态损伤.

3.1 应力空间CA砂浆损伤变化

在应力空间下，CA 砂浆损伤开始稳定发展时对应的应力大小定义为CA 砂浆的损伤应力槛值参照文献［15］，取CA 砂浆损伤程度为0.05时对应的应力作为CA 砂浆的损伤应力槛值.通过分析计算可知，不同应变率下CA 砂浆损伤应力槛值σk及其与平均抗压强度σc的比值Rσ（Rσ＝σk／σc）如表4所示.

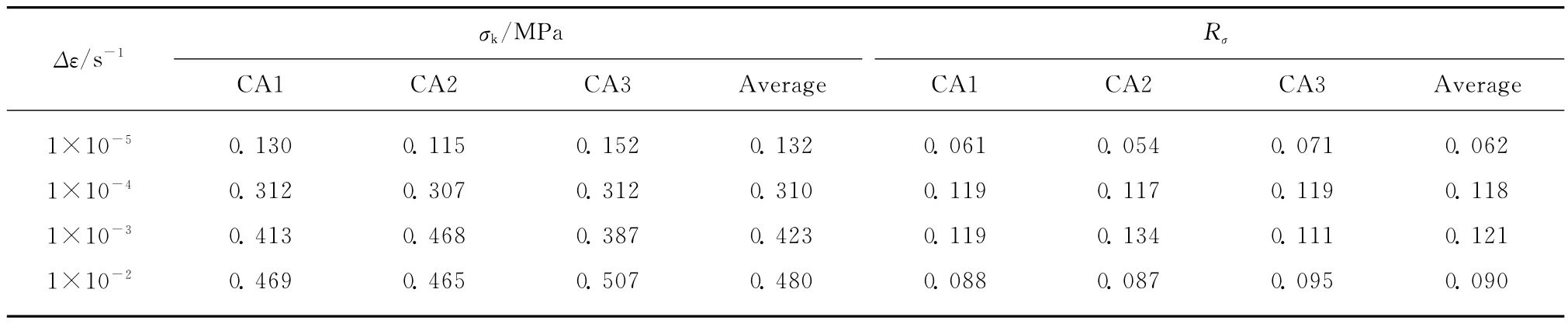
表4 CA砂浆的σk及RσTable 4 σk and Rσ of CA mortar

由表4可知，随着应变率的增大，损伤应力槛值增大.这说明在高应变率下，CA 砂浆内部裂缝的发展相对低应变率下出现滞后现象，这是由于CA 砂浆中沥青的存在使CA 砂浆的应力与应变之间存在滞后效应，且应变始终落后于应力1 个相位［14］.以1×10－5s－1的应变率作为准静态应变率，应变率1×10－4，1×10－3，1×10－2s－1下的平均损伤应力槛值分别增加了134.85%，220.45%，263.64%.当应变率增大到一定值以后，应变率对损伤应力槛值与平均最大应力的影响不再明显.产生这一结果的原因是高应变率时CA 砂浆中乳化沥青的黏性阻碍了CA 砂浆内部微裂缝的产生与发展，从而导致CA 砂浆损伤应力槛值不断增大，同时这种阻碍作用也增大了CA 砂浆的抗压强度，因而当应变率增大以后，CA 砂浆损伤应力槛值与平均抗压强度的比值Rσ受应变率影响不大.

3.2 应变空间CA砂浆损伤变化

在应变空间下，CA 砂浆损伤开始稳定发展时对应的应变大小定义为CA 砂浆的损伤应变槛值εk.文中依然取CA 砂浆损伤程度D＝0.05时对应的应变为CA 砂浆的损伤应变槛值.通过对CA 砂浆损伤程度随应变水平比（不同应变率下CA 砂浆应力－应变曲线上升段中任一应力对应的应变与相应临界应变εc的比值）的分析计算，将不同应变率下CA 砂浆损伤应变槛值εk及其与平均临界应变εc的比值Rε（Rε＝εk／εc）列于表5.

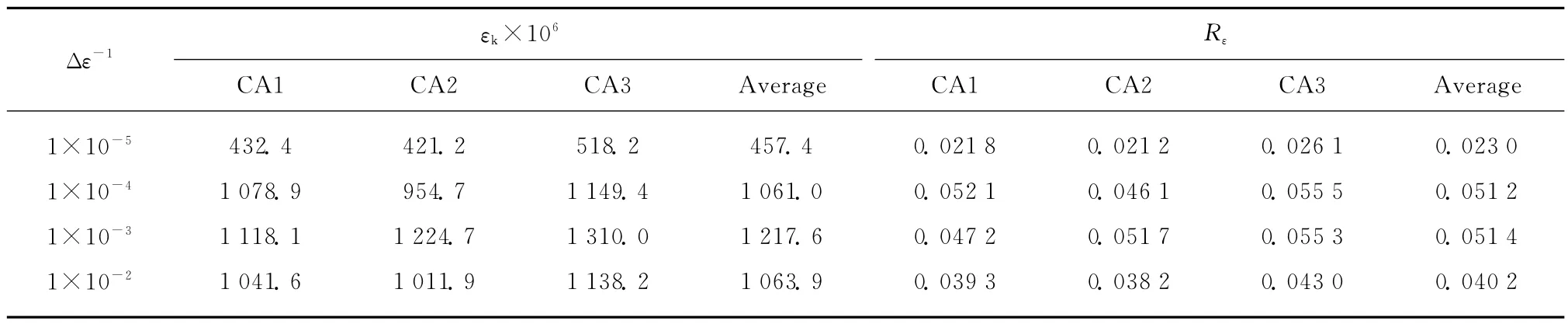
表5 CA砂浆的εk及RεTable 5 εk and Rε of CA mortar

由表5可知，随着应变率的增大，CA 砂浆损伤应变槛值εk及Rε呈先增大后稳定的趋势.产生以上结果的原因是在高应变率作用下，CA 砂浆内部的黏性阻碍了微裂缝的产生和发展，同时也阻碍了损伤的发展，因此CA 砂浆的应变槛值较准静态应变率下的大.而在高应变率的情况下，应变率对CA砂浆的应变槛值与平均临界应变的比值Rε影响不大.

4 结论

（1）随着应变率的增大，CA 砂浆的抗压强度增大，且呈幂函数变化，采用y＝a＋bxc的幂函数对CA 砂浆抗压强度与应变率的关系进行拟合较优.

（2）随着应变率的增大，CA 砂浆的弹性模量和临界应变均呈幂函数增大.

（3）以不同的应变率加载到相同的应变时，CA砂浆在低应变率下的破坏情况更加严重.这是由于CA 砂浆是应变率敏感性材料，应变率越低，作用时间越充分，CA 砂浆的破坏情况越严重.

（4）以切线模量的退化来度量CA 砂浆的损伤程度.随着应变率的增大，CA 砂浆损伤应力槛值及损伤应变槛值均增大，且当应变率较高时，CA 砂浆损伤应力槛值与平均抗压强度的比值、损伤应变槛值与平均临界应变的比值均变化不大.

［1］ESVELD C.Low－maintenance ballastless track structures［J］.Rail Engineering International，1997，26（3）：13－16.

［2］刘学毅，赵坪锐，杨荣山，等.客运专线无砟轨道设计理论与方法［M］.成都：西南交通大学出版社，2010：1－10.LIU Xueyi，ZHAO Pingrui，YANG Rongshan，et al.Design theory and method for ballastless track on passenger dedicated line［M］.Chengdu：Southwest Jiaotong University Press，2010：1－10.（in Chinese）

［3］王涛.高速铁路板式无碴轨道CA 砂浆的研究与应用［D］.武汉：武汉理工大学，2008.WANG Tao.Research and application on CA mortar in ballastless slab track of high speed railway［D］.Wuhan：Wuhan University of Technology，2008.（in Chinese）

［4］COENRAAD E.Recent development in slab track［J］.European Railway Review，2003，9（2）：81－85.

［5］SHIGERU M，HIDEYUKI T，MASSAO U，et al.The mechanism of railway tracks［J］.Japan Railway and Transportation Review，1998，15（3）：38－45.

［6］KATSUOSHI A.Development of slab tracks for Hokuriku Shinkansen line［J］.Quarterly Report of RITI，2001，42（1）：35－41.

［7］MURATA O.Overview of recent structure technology R＆D at RTRI［J］.Quarterly Report of RTRI，2003，44（4）：133－135.

［8］SONG H，DO J Y，SOH Y S.Feasibility study of asphaltmodified mortars using asphalt emulsion［J］.Construction and Building Materials，2006，20（5）：332－337.

［9］蔡成标，翟婉明，王开云.高速列车与桥上板式轨道动力学仿真分析［J］.中国铁道科学，2004，25（5）：57－60.CAI Chengbiao，ZHAI Wanming，WANG Kaiyun.Dynamic simulation of interactions between high－speed train and slab track laid on bridge［J］.China Railway Science，2004，25（5）：57－60.（in Chinese）

［10］江成，范佳，王继军.高速铁路无碴轨道设计关键技术［J］.中国铁道科学，2004，25（2）：43－48.JIANG Cheng，FAN Jia，WANG Jijun.Key techniques of ballastless track design on high－speed railway［J］.China Railway Science，2004，25（2）：43－48.（in Chinese）

［11］王发洲，刘志超，胡曙光.加载速率对CA 砂浆抗压强度的影响［J］.北京工业大学学报，2008，34（10）：1059－1065.WANG Fazhou，LIU Zhichao，HU Shuguang.Influence of loading rate on compressive strength of CA mortar［J］.Journal of Beijing University of Technology，2008，34（10）：1059－1065.（in Chinese）

［12］孔祥明，刘永亮，阎培渝.加载速率对水泥沥青砂浆力学性能的影响［J］.建筑材料学报，2010，13（2）：187－192.KONG Xiangming，LIU Yongliang，YAN Peiyu.Influence of loading rate on mechanical properties of cement asphalt mortars［J］.Journal of Building Materials，2010，13（2）：187－192.（in Chinese）

［13］谢友均，曾晓辉，邓德华，等.铁路无砟轨道水泥乳化沥青砂浆力学性能［J］.建筑材料学报，2010，13（4）：483－486，528.XIE Youjun，ZENG Xiaohui，DENG Dehua，et al.Mechanical characteristics of China railway track system（CRTS）Ⅰtype slab tracks CA mortar under different strain rates［J］.Journal of Building Materials，2010，13（4）：483－486，528.（in Chinese）

［14］刘永亮，孔祥明，阎培渝.水泥－沥青胶凝材料动态力学行为的初步研究［J］.工程力学，2011，28（7）：53－58.LIU Yongliang，KONG Xiangming，YAN Peiyu.Investigation on dynamical mechanical behaviors of cement－asphalt binders［J］.Engineering Mechanics，2011，28（7）：53－58.（in Chinese）

［15］肖诗云，张剑.不同应变率下混凝土受压损伤试验研究［J］.土木工程学报，2010，43（3）：40－45.XIAO Shiyun，ZHANG Jian.Compressive damage experiment of concrete at different strain rates［J］.China Civil Engineering Journal，2010，43（3）：40－45.（in Chinese）